基于改進粒子群模糊神經網絡的信用評估

熊志斌

（華南師范大學 數學科學學院，廣州 510631）

0 引言

由于信用風險度量的復雜性與非結構性，使得傳統的統計計量模型在風險評估中的效果往往不盡人意。近年來，神經網絡以其靈活的學習能力和優良的非線性建模等特性而受到研究人員的高度重視，并在信用評估領域中得到了廣泛運用[1]。然而神經網絡存在“黑箱操作”、結果解釋性差等缺陷而讓人詬病。隨著研究的不斷深入，有研究者開始將具有邏輯推理功能，擅長處理不確定性、不精確信息的模糊邏輯與神經網絡相結合起來，來改善上述缺陷，并在風險管理研究的實踐中取得了較好的效果[2,3]。不過上述模型中優化模型參數的方法為BP算法或是基于梯度下降的尋優算法，這種模型并未解決一般神經網絡所存在的學習速度緩慢、易陷入局部最優等缺陷。而以粒子群算法為代表的群智能優化算法是用搜索空間中的點模擬自然生物中的個體，將生物的優勝劣汰過程或覓食過程類比為可行解變換優化的迭代過程，該算法相比BP等梯度算法而言具有全局性能良好、操作簡單且易于實現的優點[4]。然而，粒子群算法也存在著不能兼顧收斂速度、全局探索能力和局部精細搜索能力的問題，在迭代后期易出現“早熟”現象[5]，針對上述缺陷，一個改進思路就是綜合不同算法技術，使得不同方法技術之間相互補充、相互促進，最終達到改善優化算法的性能，提高模型預測效果的目的。

基于此，本文提出一種改進的粒子群算法——混沌小生境粒子群算法，來改善上述缺陷。首先基于混沌運動的遍歷性特點，在算法初始化時采用混沌迭代產生粒子的初始位置和速度以提高種群的多樣性；然后借鑒遺傳算法中的常用的小生境技術來改進粒子群算法在進化過程中的多樣性，提高算法的全局尋優性能和收斂速度。通過這種改進算法對模型參數進行優化，構建了混沌小生境粒子群模糊神經網絡模型，并運用該模型對我國上市公司信用風險狀況進行評估預測。

1 模糊神經網絡結構

本文所采用的模型為四層網絡模型結構，具體結構如圖1所示，其中n為輸入維數，m為模糊子集的個數，wj是模糊推理層第j個節點到輸出層節點的耦合權值。這里用分別表示第l層第i個節點的輸入和輸出。

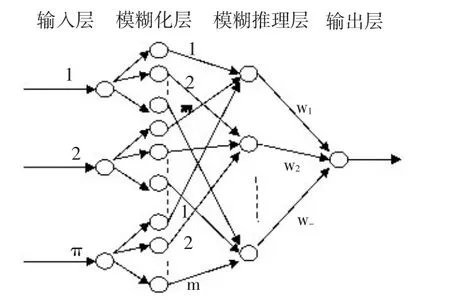
圖1網絡模型結構

每層的輸入和輸出具體表達如下：

（1）第一層（輸入層）：這一層有n個節點，這些節點僅僅將輸入值傳遞到第二層。

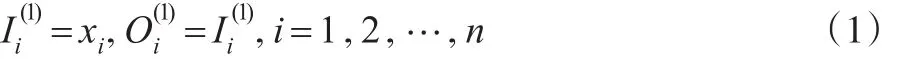
（2）第二層（模糊化層）：這一層共有mn個節點，共有n組。每個節點與輸入變量的一個語言變量標識相對應，隸屬值確定了輸入變量的模糊集程度。本文采用Gaussian隸屬函數。

其中 μij（xi）是模糊變量隸屬函數，mij,σij分別為Gaussian函數μij的中心和寬度。

（3）第三層（模糊推理層）：該層共有m個節點，其輸入輸出表達式為:

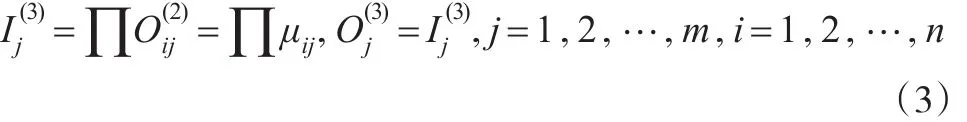
（4）第四層（去模糊化層）：1個節點，該節點計算前一層輸出之和并將其作為總輸出。

其中wj是第三層第j個節點到第四層節點的耦合權值。

2 混沌小生境粒子群優化算法

2.1 標準粒子群算法

在標準的PSO算法中，其解的好壞是由適應度函數值來評價，適應度函數的設計與目標函數有關，要根據實際研究問題來確定。種群中的每個粒子都代表一個可能解，它包括粒子自身所處位置及速度，粒子速度決定了其搜索的更新方向和距離。粒子在搜索過程中，是通過跟蹤個體最優位置（即個體極值pbest）和全局最優位置（即全局極值gbest）來更新自身的。在標準PSO算法中，粒子的位置和速度根據如下方程進行更新[4]：

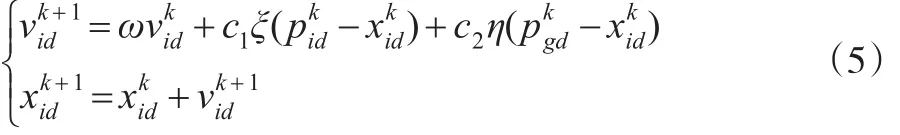
2.2 混沌小生境粒子群算法

一般來講，由確定性方程得到的具有隨機性的運動狀態都可稱為混沌，其中Logistic映射就是一個典型的混沌系統[7]，其迭代公式如下：

其中，k=1,2,3,…,α為控制參數，α∈（2,4]。在這里，本文主要是利用混沌運動的遍歷性，即通過混沌迭代產生大量的初始群體，從中選出較好的初始群體。

小生境技術是通過強迫個體分布在不同“生境”的方法，增加個體多樣性，避免算法陷入局部極值無法跳出。本文將基于限制競爭選擇策略（Restricted Competition Selection，RCS）的小生境技術與粒子群算法結合起來，構建小生境粒子群算法（niche evolution PSO，NEPSO）來改進算法的搜索精度和尋優性能。RCS策略的主要優點是能夠將小生境范圍內的兩個解中較差的淘汰掉，保證種群朝最優解方向運動；另外，RCS策略是以種群最優位置之間的距離作為小生境之間的距離，當兩個生境距離小于某一設定的閾值時，較好的生境予以保留，而對于較差的種群進行重置，即將種群內最優個體作為種群的最優極值，并重新初始化種群內的其他被選中粒子。這樣既保證了搜索朝著最優方向進行，又使得每個小生境種群間的搜索是相互獨立的，保證了多樣性，而且當生境發生相互干擾時，該策略僅需對極少數幾個最優個體粒子進行控制，極大減少了算法復雜度，提高了算法效率。RCS策略更詳細的介紹可參看文獻[8]，這里不再贅述。

這里，本文引入RCS小生境技術來改進粒子群算法的尋優性能，通過以下粒子狀態更新方程來對粒子狀態進行更新，既防止不同種群趨同，又保證種群的多樣性，粒子狀態更新方程如式（7）：

混沌小生境粒子群算法（CNEPSO）的具體步驟如下：

步驟1：產生初始種群和若干小生境子種群；初始化算法參數，包括慣性權重ω，隨機數ξ1、ξ2和ξ3，學習因子c1、c2和c3等；

步驟2：進行混沌初始化。對每個種群都隨機產生一個n維的每個分量數值都在0和1之間的向量yo=（y01,y02,…,yon），yi（i=1,2,…,N）由式（6）給出，其中N為種群規模；然后再根據式子 xij=xmin+yij（xmax-xmin），（i=1,2,…,N；j=1,2,…,n）計算粒子的位置，通過計算目標函數，從N個初始群體中找出較好的m個解作為初始位置，隨機產生m個初始速度；

步驟3：對所選出的粒子，根據當前位置和速度產生出新的位置；

步驟4：對每個子種群中的每個粒子評價其當前的適應值。這里使用誤差平方和（SSE）的倒數作為評價函數，即，以自身當前位置作為每個粒子的個體極值，以每個子種群中的最優粒子作為子種群的最優極值，所有粒子中最優粒子則被視為整個種群中的全局最優極值

步驟5：執行RCS小生境技術策略，確定每個小生境子種群中的最佳個體粒子，每個子種群中的最佳粒子被選中重新組成一個新的種群Newgroup；

步驟6：對每個子種群內（不含Newgroup）的個體按式（7）進行更新（包括位置和速度）；

步驟8：每個種群按小生境技術操作，不斷迭代，當迭代一定次數時，對最差的子種群重新初始化；

步驟9：當迭代一定次數后，計算種群Newgroup內所有粒子適應度值，并按標準PSO的粒子更新方程式（5）更新粒子位置和速度；

步驟10：檢查是否滿足算法終止條件。本文使用兩條學習終止準則：1）誤差平方和MSE；2）最大進化代數M。若MSE＜ε（這里ε為事先設定好的值）或M達到預先設定的迭代次數，則中止算法并輸出結果；否則，令k=k+1，轉到步驟6直到終止條件滿足。

3 信用評估建模實例

3.1 樣本來源與數據預處理

本文以我國上市公司中ST公司（包括*ST公司）和非ST公司作為研究對象，根據唐振鵬等（2016）的觀點[9]，雖然ST、非ST公司與公司信用好壞并不完全等同，但它們之間有著很強的相關性，在上市公司信用研究中可以把ST公司視為信用差（危機）公司，非ST公司視為信用好（正常）公司，本文采用了這種觀點。本文樣本數據來源于Wind數據庫和同花順財經數據庫，由于公司t年被宣布ST處理和該公司公布t-1年度財務報表幾乎是同時發生的，故本文采用t-2年的財務數據來預測t年是否會被ST，例如2014年被宣布ST的公司，則采用2012年財務數據來進行分析。本文在借鑒國內外有關文獻的基礎上，并結合指標的可比性、同趨勢性原則，選取了10個指標，即：資產凈利率（X1），主營業務利潤率（X2），凈資產利潤率（X3），資產負債率（X4），速動比率（X5），已獲利息倍數（X6），經營現金總債務比（X7），總資產周轉率（X8），應收賬款周轉率（X9），主營業務收入增長率（X10）。

對于原始指標數據，本文進行了歸一化處理，歸一化函數如式（8）所示：

這里，X代表輸入矩陣，max x和min x分別為X中的最大和最小值。由此可知，該網絡模型的輸入層節點為10，模糊子集數設為3，網絡模糊化層節點數則為30，去模糊化層節點數設為3，輸出變量為單變量y，即輸出層為一個節點，若y=1則代表信用差（ST公司），y=0則代表信用好（非ST公司）。因此，該模型的結構為一個10-30-3-1網絡結構。

3.2 交叉驗證與模型參數選取

為了盡量減少隨機劃分訓練樣本集和測試樣本集所可能帶來的偏差，同時也為了提高模型的泛化能力，更有效地檢驗模型的準確性和可靠性，本文采用n重交叉驗證（n-fold cross-validation）方法來評估模型對信用風險分類的有效性。具體方法為：初始樣本集合（300家公司）被劃分成5組互不相交的子集，每組樣本數都為60家（14家ST和46家非ST公司）。每一次模型在除了一個子集之外的其他子集上進行訓練，而未被訓練的子集則用來作為測試集。整個過程被重復5次試驗，每次使用一個不同的子集進行驗證，所構建模型總的分類準確度是通過這5次試驗中所得到的分類準確度加總后的簡單平均值求得。

在本文中，種群大小被設定為60，初始子種群數為3，ξ1、ξ2和ξ3為[0,1]區間內均勻分布的隨機數；慣性權重ω取值區間為[0.4,0.9]；學習因子 c1=1.5,c2=0.2，c3=0.5；xmin=-10，xmax=10；vmax=8；樣本學習中止條件：①MSE＜0.001；②最大迭代數為5000。

3.3 實證結果

本文通過5重交叉驗證的方法來驗證所構建的混沌小生境粒子群模糊神經網絡（CNEPSO-FNN）的有效性，具體結果見表1。

表1 CNEPSO-FNN模型交叉驗證結果

表1中，0代表信用好的公司，1代表信用差的公司。0-0表示正確區分出信用好的公司的準確率或樣本數，1-1表示正確區分出信用差的公司的準確率或樣本數。從表1可看出，模型對5組平均分類準確率分別達到93.33%、95.00%、93.33%、93.33%和91.67%，對整個樣本的平均分類準確率達到了93.33%，效果相當不錯。

作為對比，本文在構建CNEPSO-FNN模型同時，還另外分別構建BPNN和SPSO-FNN（采用標準PSO算法優化模糊神經網絡）兩種模型。表2給出了這三種模型對總體樣本預測準確率的對比結果。

表2 三種模型的測試對比結果

與表1一樣，表2中0-0表示正確區分出信用好的公司的準確率或樣本數，1-1表示正確區分出信用差的公司的準確率或樣本數。正如表2所示，BPNN和SPSO-FNN模型在300個樣本中預測正確的樣本數分別為228和251，預測準確率分別為76.00%和83.67%，而CNEPSO-FNN模型預測準確的樣本數為280個，準確率達到了93.33%，遠高于前兩個模型，也說明構建的CNEPSO-FNN模型的有效性和可靠性。

4 結論

本文提出了一種改進的粒子群算法，即將混沌技術、小生境技術與粒子群算法結合構建了混沌小生境進化粒子群優化算法。首先利用混沌遍歷性特點，采用混沌迭代初始化粒子的位置和速度，接著在一般小生境技術的基礎上，為了避免小生境的相互重疊，采取了淘汰策略對距離太近的小生境進行淘汰，通過淘汰策略使得過于接近以至重疊的小生境重新分化與組合，以便各個小生境保持獨立的搜索空間。通過這種改進，改善了種群的多樣性，提高了算法的全局尋優能力。將這種改進的粒子群算法與模糊神經網絡模型相融合，構建了改進的粒子群模糊神經網絡——混沌小生境粒子群模糊神經網絡，并利用中國上市公司數據，進行了信用評估預測，實證檢驗結果也表明了該評估模型的有效性和可靠性，該研究成果也為探索符合我國實際的信用評估技術方法提供了一些參考和借鑒。