基于季節性特征分析的鐵路煤炭運輸預測方法

向思桐，祝繼常，宮薇薇

（中國鐵道科學研究院a.研究生部；b.運輸及經濟研究所，北京100081）

0 引言

對時間序列進行季節調整在經濟計量方面的應用受到了廣泛關注，經濟統計中的月度和季度數據或大或小都含有季節變動因素，它往往遮蓋了經濟運行中的客觀變化規律如發展趨勢等，很大程度上影響了進一步的研究與預測。

借鑒相關學者的研究[1-5]，本文考慮到同一品類貨物、不同地區表現出的季節性特征各不相同，在全國范圍內進行分析將得到不同地區季節性疊加后的結果，不能很好地反映某一地區某一品類的貨運量波動；以往的季節性研究往往以月度數據作季節性分解，然而季節性特征的實質是某一品類貨物在氣候相似的三個月內，所具有的相同特征加和后表現出的顯著效應，對月度數據進行季節性分解將削減這種效應。因此，本文嘗試對煤炭單一品類、在各地區表現出的季節性特征進行以季節為時間節點的確定性因素分解，并分析煤炭運輸表現出季節性特征背后的經濟與市場原因，在此基礎上借助Holt-Winters模型其進行季節調整后的運量預測。

1 數據處理與分析方法

1.1 數據透視表

本文所使用的數據為全國各鐵路局（公司）的月度煤炭運輸數據，數據時間范圍為8年（96個月）。如果僅僅限于月度數據分析，將使運量的季節性特征不能清晰、直觀地顯現出來。因此本文運用數據透視表工具，按照月度周期和季節周期兩種不同的方式，對所研究區域的數據，提取相應的時間序列，進行篩選和重點分析，從時間、地域兩個維度對數據進行有效的處理。

1.2 確定性因素分解法

確定性因素分解法是一種基于經驗模型的分析方法，該方法需要依靠統計工具實現，運用該方法可以將某一時間序列各個影響因素分解開，從而針對其中某一個因素進行分析。其經驗模型如下：

（1）乘法模型

（2）加法模型

式中，Tt代表序列的長期趨勢波動；st代表序列的季節性變化；It代表隨機波動。選用加法模型或乘法模型取決于三種因素的相互作用關系。由于貨物運輸三種因素同時存在相互作用影響，符合乘法模型的假設，且相關文獻表明，運用乘法模型分析貨物運輸效果較優，因而本文選用乘法模型。

本文基于R統計軟件，運用該方法將某一時間序列的長期趨勢、季節因素和隨機因素分解，提取相應季節指數，著重分析季節性特征。

1.3 Holt-Winters模型

Holt-Winters模型是將含有線性趨勢、季節特征和隨機波動的時間序列分解，并用指數平滑分別對其長期趨勢、趨勢增量和季節變動進行估計[6]，其本質是一種三參數指數平滑法。該方法不僅可處理同時具有趨勢和季節性變化的數據，還能適當地過濾掉隨機波動的影響。Holt-Winters模型分為乘法模型和加法模型，其模型簡述如下：

（1）乘法模型

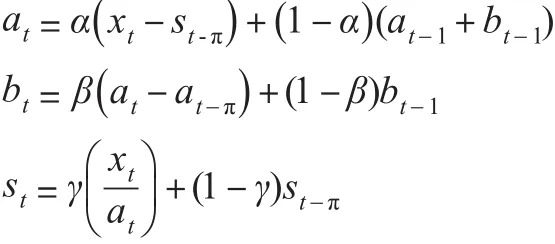
（2）加法模型

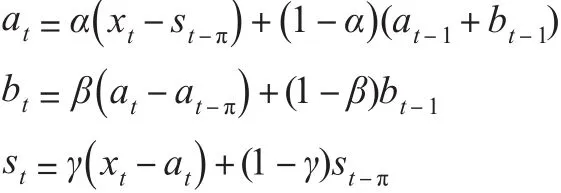
其中，at為該序列的水平部分，bt為該序列的趨勢部分，st為該序列的季節因子（假設一個季節周期長度為π），這個季節因子可以跟隨每年的具體情況波動。

在確定性因素影響很強勁時，選擇合適的確定性因素模型通常會得到較滿意的分析預測效果。由于確定性因素分解法原理與Holt-Winters模型的構造原理相契合，因此本文選用Holt-Winters模型對典型地區數據的時間序列進行實證分析。

2 全路煤炭運輸的季節性特征

對2009—2016年8年間全路煤炭運輸數據繪制時序圖，運用數據透視表對數據重組，將運量以季節為時間節點進行繪制。按照傳統的季節劃分方法，每年的3、4、5月為春季，6、7、8月為夏季，9、10、11月為秋季，12、1、2月為冬季。借助六次多項式對煤炭運量繪制趨勢線，擬合多項式為y=26.042x6-2398.2x5+83582x4-1E+06x3+1E+07x2-1E+07x+3E+08,擬合優度在0.9057，所得折線圖如圖1所示。

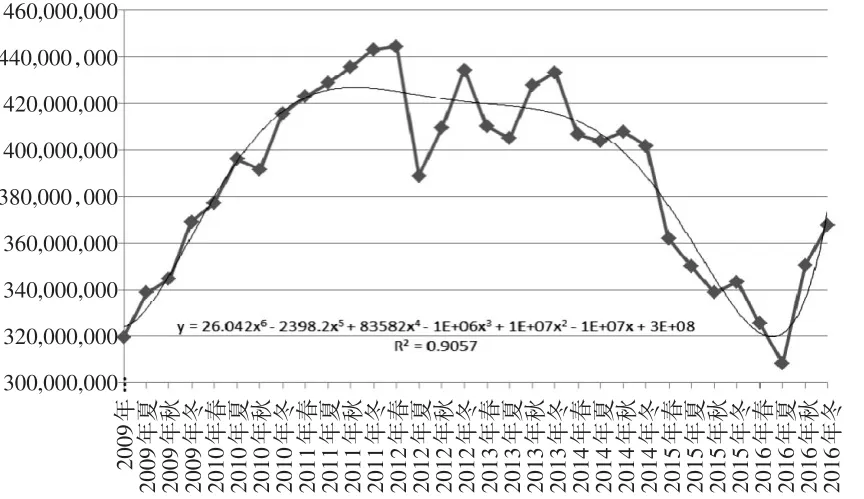
圖1全路煤炭運輸季節時序圖

由圖1中趨勢線可以看到2009—2016年我國鐵路煤炭運量經歷上升、緩降、下跌、回暖的總體趨勢。產生這種情況的原因如下：

（1）“迎峰度夏”和“迎峰度冬”本是短缺經濟的反映。2009—2011年期間，經濟剛剛開始復蘇，用煤需求旺盛，庫存低位運行。因而每到夏、冬兩季，煤炭供應偏緊，需要大量通過鐵路運輸以保證煤炭供應。

（2）“迎峰度夏”和“迎峰度冬”季節性規律的消失也正是過剩經濟的反映。2012年以后，國內煤炭市場供需關系出現反轉，煤炭供大于求的格局在此后一直存在，庫存長期高位運行。在此情況下，若供大于求的市場狀況不變，則鐵路煤炭運輸不會再出現季節性高峰。

作為典型的周期性行業，煤炭行業在經驗認知中具有很強的季節性，然而由于宏觀經濟環境的不斷變化，季節性周期對全路煤炭運輸來講，不再是具有很高指導性的規律。

3 典型地區煤炭運輸季節性特征

雖然全路煤炭運輸季節性特征不顯著，但我國不同地區有不同的煤炭消費狀況。本文運用確定性因素分解法研究發現，部分地區鐵路煤炭運輸仍表現出顯著的季節性特征，總結歸納為以下兩種主要類型：

（1）秋高峰、春低谷型；

（2）冬高峰、夏低谷、春秋平衡型。

3.1 秋高峰、春低谷型季節性特征分析

運用R統計軟件對秋高峰、春低谷型地區煤炭運輸月度數據做ACF圖如圖2所示。

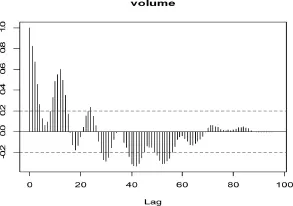
圖2秋高峰、春低谷型季節性特征ACF圖

由圖2可知，序列自相關系數并未在2倍標準差范圍以內波動，因而該序列并非平穩時間序列；自相關圖上顯示自相關系數先為正、后為負，可知該時間序列具有趨勢性，并且可見明顯的正弦波動規律，這是具有周期變化規律的非平穩序列的典型特征，因而判斷該序列有趨勢和季節性特征。

運用R統計軟件使用季節數據對該時間序列進行確定性因素分解，見圖3。

圖3秋高峰、春低谷型時間序列確定性因素分解圖

圖3由上至下分別為原時間序列圖、趨勢圖、季節因素圖、隨機因素圖。由圖3可以觀察出該序列呈先上升、后下降的整體趨勢，季節因素圖則存在顯著的高峰和低谷。為更清晰地觀察高峰和低谷的所在季節，提取出春、夏、秋、冬四個季節的季節指數分別為：0.900553868、0.937327793、1.083830191、1.078288148。比較四個季節指數，秋季季節指數最高，春季季節指數最低，該序列表現出的特征概括為秋高峰、春低谷，時序圖見下頁圖4。

圖4秋高峰、春低谷型煤炭運輸時序圖

秋高峰、春低谷型季節性特征表現在我國黑龍江地區，根據黑龍江地區的地理與人文環境，形成這一特征的原因分析如下：黑龍江地區緯度較高、氣候嚴酷，冬季需要儲存冬暖煤以越冬，供暖時間達到半年及以上。其中部分城鎮由每年9月開始供暖，到次年5月結束。因此可以觀察到由夏入秋的顯著驟升趨勢。每當春季來臨，1/3左右的熱電企業設備經過半年左右的運轉，需停產檢修，使得春季煤炭的消耗量驟減，并且煤炭資源在空氣中暴露易遭受風化和雨水沖刷等侵蝕損耗。因此，熱電企業在春季到來會加快煤炭庫存的消耗，并盡量不再存儲煤炭。

綜上所述，該地區煤炭運輸形成了秋高峰、春低谷型季節性特征。

3.2 冬高峰、夏低谷、春秋平衡型季節性特征分析

該類型月度數據做ACF圖過程同上，不再贅述。全國有三個地區煤炭運輸符合該型季節性特征，分別為遼寧（包含吉林部分地區）、廣西和內蒙古等三個地區。對此三個時間序列進行確定性因素分解如圖5所示。

圖5冬高峰、夏低谷、春秋平衡型時間序列確定性因素分解圖

由圖5可以觀察到，遼寧與廣西地區煤炭運輸均呈先上升、后下降的整體趨勢，但廣西地區下降后運量高于起始運量，而遼寧地區則低于起始運量；內蒙古地區的整體趨勢為先上升、中段持平、最后下降，下降后運量低于起始運量。同樣，提取三個地區的季節指數如表1所示。

表1 冬高峰、夏低谷、春秋平衡型特征季節指數

由表1中季節指數可知，三個地區均表現為冬季季節指數最高、夏季季節指數最低、春秋季介于二者之間且數值接近，因此該型季節性特征可概括為冬高峰、夏低谷、春秋平衡。

根據這三個地區的地理與人文環境，形成這一特征的原因分析如下：

（1）遼寧與內蒙古均屬于北方供暖地區，但與黑龍江相比其緯度較低，春秋兩個季節較長，供暖時間縮短。遼寧、內蒙古由秋季中、末期開始供暖，煤炭運量開始上升，但未達到峰值，從而在冬季和夏季間呈過渡形態。每逢冬季，兩個地區均需運送大量冬暖煤炭；直到第二年夏季，煤炭需求減少運量出現低谷。

（2）廣西屬貧煤地區，煤炭主要依靠進口與外省調入[7]。廣西地區無需供暖，煤炭消耗主要用于工業和發電。由于地處我國南方，水能資源豐富，諸多水力發電企業在水能豐富的夏季使用水力發電，熱力發電作為補充，因而夏季的煤炭消耗量較小，運量呈現低谷；待到冬季，水能資源不再豐富，電煤需求量增大，運量也隨之出現高峰。

綜上所述，雖然這三個地區地理與資源環境不同，但都表現出相同的冬高峰、夏低谷、春秋平衡型季節性特征。

4 Holt—Winters模型擬合與預測

對煤炭運輸時間序列分析的目的，在于明確確定性因素對煤炭運輸的影響，科學預測鐵路運輸市場需求，這對于提高運輸組織效率和提升運輸服務質量具有積極的指導意義。基于上文所得出的結論，選用與因素分解法乘法模型原理相符的Holt-Winters乘法模型，對典型地區的煤炭運輸數據進行擬合，以檢驗Holt-Winter乘法模型的使用效果。

運用R統計軟件對建立的模型求解，執行算法部分代碼如下：

得到遼寧地區運輸數據Holt-Winters三參數指數平滑擬合結果見表2。

表2 遼寧地區數據指數平滑參數

其中，α為當前點的水平部分參數，β為趨勢部分參數，γ為季節部分參數。三個參數的取值范圍都在0～1之間，數值越接近0，近期觀測值對當前點的影響權重就越小。本例中α值相對較高，表明當前點的水平部分受近期數據影響較大；β為0表明趨勢部分的斜率在整個時間序列上不變，且等于初始值；γ值沒有顯著偏向某一方，表明在該例子中季節趨勢的擬合和預測是綜合了遠期與近期的觀測值。該序列繪制擬合曲線與實際曲線見圖6。

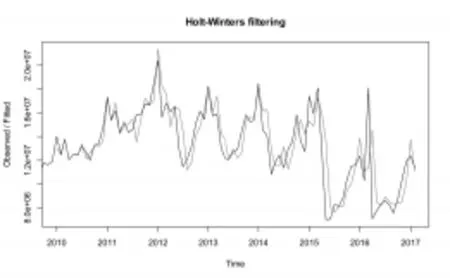
圖6遼寧地區Holt-Winters模型擬合效果圖

可以發現擬合結果基本合理，將誤差絕對值按降序排列，得到遼寧地區擬合誤差分析表（表略）。

排列結果顯示，Holt-Winters模型自2010年起共擬合84條數據。其中72條擬合數據與原數據的誤差在絕對值15%范圍內隨機波動，可以判斷該誤差為隨機誤差，而非系統性誤差。誤差最大的6條數據集中發生在12年夏季、15年春季與16年春季，由前文分析知這三個時間段由于宏觀經濟環境改變對煤炭運量產生的決定性影響掩蓋了季節效應，從而產生較大誤差，在實際預測中宏觀經濟環境需單獨考慮。其余六條誤差絕對值在15%范圍外的數據其誤差影響因素尚不清楚，多發生于某季節結束或開始前后一個月，但不排除模型本身的平滑效應與其他因素綜合產生影響。

由上述分析知該模型預測峰值效果較好，對整體趨勢擬合效果較好，可見運用確定性因素分解法對煤炭運輸時間序列進行分析可以得到不錯的效果。該模型很好地保留了序列的整體趨勢因素與季節波動因素，缺點是存在一定的滯后性，對除季節因素外的其他因素無法進行加權考慮。

調用R統計軟件中forecast函數包，運用該模型對2016年1月到2017年2月14個月的運量做預測，輸入代碼如下：

將預測值與實際值相比較如圖7所示。

由圖7可知，除3、4、5月運量出現驟增驟減超過置信區間外，其余月份均在80%置信區間內，可以判斷該模型運用合理，不存在方向性錯誤，且預測結果合理可靠。利用該方法對實際運量進行預測，可以得到相應的運力配置區間指導生產。

5 結論

（1）全路煤炭鐵路運輸有明顯隨經濟環境與國家調控政策相關的波動規律，但總體上無顯著季節性波動特征。在煤炭資源十分短缺的情況下，季節性特征略顯。雖然傳統認知煤炭市場具有季節性特征，然而是否可據此對全路煤炭運輸進行預測需進一步探討。

（2）地域范圍縮小后，部分地區煤炭運輸具有顯著的季節性特征，總結歸納為兩種類型，分別為秋高峰、春低谷型以及冬高峰、夏低谷、春秋平衡型。這兩種季節性特征都與所研究地區的地理與資源環境密切相關。造成秋高峰、春低谷型季節性波動的主要原因是黑龍江地區所處的地理氣候環境；對于冬高峰、夏低谷、春秋平衡型特征，南北方均有出現。

（3）Holt-Winters模型對鐵路煤炭運輸預測有較好的擬合效果，峰值預測效果較好。分析表明典型地區鐵路煤炭運輸具有明顯的整體趨勢和季節特征，符合該模型的使用前提，模型很好地保存了兩種特征并可以對未來若干周期做出可靠的預測。不同的時間序列運用Holt-Winters模型擬合優度不同。經過殘差分析，某些序列中尚有信息提取不夠充分，為提高擬合與預測精度，可以考慮對時間序列中的隨機有效信息進行充分提取后再使用。