基于混合模型的PM2.5日濃度預測

李 棟，薛惠鋒，張文宇,3，方 銘

（1.西安郵電大學a.經濟與管理學院；b.研究生院，西安 710061；2.西北工業大學 自動化學院，西安 710072；3.中國航天系統科學與工程研究院，北京 100048）

0 引言

近年來，隨著中國城市化、工業化進程的不斷加快，空氣污染問題也愈發嚴重，成為公眾關注的社會焦點問題之一。PM2.5作為空氣污染的主要組成成分，是指環境空氣中空氣動力學當量小于等于2.5um的顆粒物[1]。經研究發現，PM2.5已經是當前影響人類生存環境[1-3]和人體健康[4]的最主要污染物之一。PM2.5中含有大量的有毒有害物質，具有高活性、停留時間長、運輸距離遠的特性。研究表明，長期暴露在含有較高濃度PM2.5環境中的人，將增加患心血管[5]和肺部疾病[6]的概率。因此，及時并準確地預警PM2.5濃度，對于評估城市空氣質量，幫助人們合理安排出行具有指導意義，同時能為政府治理PM2.5污染的提供依據。

為了準確預測PM2.5的日均濃度，本文提出了一個基于自回歸分布滯后模型（ARDL）、果蠅優化算法、核極限學習機的PM2.5日均濃度混合預測模型。為了驗證混合模型的有效性，選用了2016年1月1日至2017年5月31日陜西省關中地區五地市（西安、寶雞、咸陽、渭南和銅川）的PM2.5、PM10、CO等空氣污染物、以及相關氣象因子的歷史數據，從日維度進行了PM2.5濃度預測，預測結果顯示混合模型具有良好的預測能力，可為陜西省關中地區開展空氣污染預警和城市綜合管理提供理論支持和決策依據。

1 材料與方法

1.1 研究區域

關中又稱為關中平原，它位于陜西中部，海拔在323～800米之間，東西長約350公里，面積約為3.6萬平方公里，是中國四大平原之一。關中平原介于橫貫陜西的秦嶺和渭北北山山系之間，南北寬窄不一，東部最寬達100公里，在西安附近時南北寬度縮為75公里，至寶雞市西部逐漸閉合成峽谷，這種東寬西窄，周邊高平原低的地形條件不利于污染物擴散。隨著以西安為中心的關中地區工業化和城市化進程的加速發展，人為活動日益頻繁造成污染物排放量的大幅增加，關中地區空氣質量日趨惡化。根據2016年全國霧霾城市排名顯示，關中五地市PM2.5日均濃度均排在前70名，其中西安排名最高，位于第34位，銅川排名最低位于63位，關中地區已經成為中國區域性大氣污染較為嚴重的區域之一。

1.2 研究數據

為了加強對關中地區PM2.5等污染物的監測和治理，為居民提供實時的污染狀況信息，陜西省環保廳在關中地區共設置70個監測點，其中西安有18個監測點、咸陽有15個監測點、寶雞有17個監測點、銅川有7個監測點、渭南有13個監測點，涵蓋了關中地區中各類型區域，這些監測點能夠實時監測各種污染物的濃度數據，通過陜西省環保廳網站進行公布。本文中涉及的各市污染物數據均來自該網，并進行了后期整理。PM2.5預測研究中除了需要空氣中的各種污染物數據外，還需要溫度、濕度、風速等各種氣象因子數據，這部分數據則是通過陜西省氣象局網站獲取并進行相應整理。

1.3 研究方法

1.3.1 相關分析與因子定階

相關分析（CA）是研究PM2.5與其他污染物及氣息因子之間是否存在某種依存關系，測度各因子之間關系密切程度的一種統計方法。由于收集到的污染物種類及氣象因子較多，如全部引入預測模型，則預測模型勢必受到非必要因素的影響，增加預測模型復雜度。因此，需要通過相關分析識別哪些因素與PM2.5濃度相關性較高，從而將這部分因素從眾多因素中篩選出來，作為預測模型的輸入。

在預測模型中，不僅要明確PM2.5的影響因子有哪些，還需要明確這些影響因子與PM2.5之間的滯后影響階數。為了解決這個問題，本文引入自回歸分布滯后模型來識別和確定各影響因子滯后階數。

自回歸分布滯后模型（ARDL）是一種較新的協整檢驗方法，其原理是利用邊界檢驗法確定變量間是否存在長期穩定的關系，若存在協整關系，則可進一步估計變量間的相關系數[7]。區別于傳統的協整檢驗方法，ARDL模型最大的優勢是其對變量平穩性要求較為寬松，只要求變量的單整階數均不超過1，即1（0）序列、1（1）序列或1（0）、1（1）混合序列均可使用該模型進行檢驗。除此之外，ARDL模型還具備小樣本適用性，解釋變量為內生變量的適用性等特點。自回歸分布滯后模型的一般形式如下：

1.3.2 KELM算法

極限學習機（ELM）[8]是一種基于單隱層前饋神經網絡的快速學習方法。該方法只需指定隱層節點數，即可通過求解線性方程組得到極小2-范數最小二乘解，并將該解作為隱層輸出權值。ELM的學習過程只有一次，相比傳統的神經網絡，ELM的網絡泛化能力和學習速度得到明顯提高。

核極限學習機（KELM）是在極限學習機（ELM）的基礎上提出了基于核函數的極限學習機，該方法將SVM中核函數的思想運用到ELM中。由于支持向量機（SVM）中的核函數映射?（x）與ELM中的隱含層節點映射h（x）的具有一定的相似性，Huang（2012）[9]提出將ELM的h（x）替換為支持向量機的核函數映射?（x），構建核極限學習機（KELM）算法，該算法解決了ELM需要確定隱含層個數的問題，且具有更好的泛化性能。

1.3.3 果蠅優化算法

已有的研究成果顯示KELM的擬合精度和泛化能力受到參數的影響。因此，需要采用適合的優化算法來對其核參數進行尋優。目前在KELM的參數尋優中主要使用的有遺傳算法[10]和粒子群優化算法[11]，這些方法雖然存在可以找到最優參數的可能性，但仍存在迭代速率慢，易陷入局部最優的問題。果蠅優化算法（FFOA）[12]是依據果蠅覓食行為設計出的一種全局優化算法。相較于粒子群、魚群等群體智能優化算法，FFOA具有參數設置少、運算速度快且易于代碼實現等優點。因此，本文采用FFOA自動搜索核極限學習機核參數，以此建立PM2.5濃度預測模型。

1.3.4 混合預測模型

鑒于PM2.5濃度預測的復雜性，本文將前面介紹的幾種方法進行混合提出了PM2.5混合預測模型。該模型首先通過相關性分析識別PM2.5與其他污染因子以及氣象因子之間的相互聯系，然后通過ARDL模型分析識別出PM2.5與各因子之間是否存在長期穩定關系，并確定各因子的滯后影響階數。通過相關性分析以及ARDL模型就可以識別PM2.5與自身以及各因子存在的各種關系，進而明確未來預測方法的輸入向量。具體的預測方法選擇上，本文通過對比選擇了KELM作為預測算法，由于KELM的泛化能力受到核參數的影響，因此本文引入果蠅優化算法使用對其核參數進行尋優，從而最終建立PM2.5混合預測模型。具體建模具體步驟如下：

（1）數據預處理。對收集到的PM2.5、SO2、NO等空氣污染物以及相關氣象因子時間序列數據進行缺失值填充。

（2）因子相關性分析。對PM2.5、SO2、NO等空氣污染物以及最高氣溫、最低氣溫等氣象因子數據進行相關分析，識別出與PM2.5濃度具有顯著相關性的因子。

（3）確定PM2.5相關因子滯后階數。利用ARDL模型檢測PM2.5與自身及相關因子之間存在的長期關系，確定各因子最大滯后階數ti（1＜=i＜=p+1）,p為識別出的與PM2.5顯著相關的因子個數，由于PM2.5自身存在滯后相關性的可能，因此i的最大值為p+1。

（4）數據重構。根據各影響因子最大滯后階數對數據進行重構，重構后的數據將作為KELM預測算法的輸入向量。重構結果如式（2）所示，式中X1（-1）指與PM2.5具有顯著相關性的第1個因子延遲1階的數據。

（5）動態生成訓練數據。本文模型是在線預測模型，即該模型會動態更新訓練數據。若指定預測t時刻的PM2.5濃度，則模型會自動將t-1時刻之前的數據（含t-1時刻）作為訓練數據。當預測時間更新為t+1時刻時，則模型自動將t時刻的各指標數據加入到訓練數據中。

（6）構建KELM初始預測模型。首先對重構數據集XR、Y進行歸一化處理，得到歸一化后數據集。接著建立單隱層神經網絡，輸入數據為，輸出數據為Y，使用KELM算法建立初始預測模型。

（7）KELM核參數優化。

①根據核參數個數確定果蠅群搜索食物的空間維度，若為2個參數，則果蠅在2維空間中搜索食物；若為3個參數，則果蠅在3維空間搜索食物。

②初始化果蠅群中各果蠅位置，或將果蠅群集中在當前最佳位置。

③果蠅群在搜索空間中自由搜素食物，每個果蠅飛翔后的位置坐標即為KELM的核參數的值。根據這些核參數值使用KELM計算訓練集的訓練精度，計算結果即為該果蠅的味道濃度（適應度值）。

④對所有果蠅的適應度值由小到大排序，找到最佳果蠅及其位置坐標。

⑤判斷是否達到優化目標，若達到則跳轉下一步。否則，繼續判斷是否達到最大優化次數，若達到則跳轉至下一步，若未達到則跳轉至步驟②繼續優化。

（8）KELM預測。依據核參數優化結果建立KELM預測模型，依據歸一化之后的相空間數據XR（t）預測t時刻的Y′（t），并將預測結果反歸一化。

（9）預測時間更新。若要繼續預測時間t+1的PM2.5濃度值，則更新預測時間為t+1，并跳轉至步驟（5）更新訓練集，然后繼續預測。

1.4 評價指標

為了衡量PM2.5混合預測模型的穩定性和適應性，選擇一些具有代表性的指標對模型的預測結果進行評價，具體指標有：平均絕對百分比誤差（MAPE）、均方根誤差（RMSE）以及可決系數R2。平均絕對百分比誤差能夠避免平均百分比誤差相比正負相抵的情況，可以更準確地反映預測值誤差的實際情況。均方根誤差對異常大的誤差反應較為靈敏，能夠較好地反映模型的預測精度。擬合優度R2能夠表達混合預測模型整體的擬合情況，當R2接近1時，表明預測值對實際值的擬合程度好，同時說明預測模型的性能較高。假設Ti為實際觀察值，Pi為預測值，各指標定義如下：

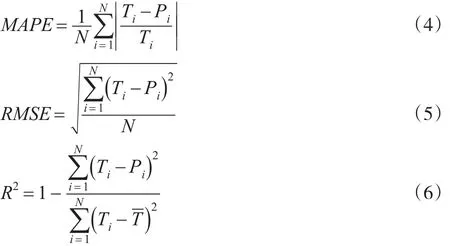
2 實例驗證

2.1 影響因子初步分析與數據收集

通過對已有研究成果進行分析后發現，影響PM2.5濃度的因素主要源于三個方面：直接生成、間接生成以及氣象因素對PM2.5的凈化衰減。其中，直接生成主要包括燃煤、汽車尾氣、工業廢氣等含有的PM2.5固態污染物；間接生成主要是空氣中的污染物通過復雜化學反應形成的PM2.5固態污染物；PM2.5的凈化衰減則是通過自身的擴散以及外界氣流、降雨等方式來實現PM2.5濃度下降。基于以上分析并考慮到數據的可獲得性，本文收集了PM2.5（μg/m3）、PM10（μg/m3）、SO2（μg/m3）、CO（μg/m3）、O3（μg/m3）、NO2（μg/m3）、RH（相對濕度%）、WS（風速m/s）、T_Low（最低溫度oC）、T_high（最高溫度oC）等10個因子數據，這些數據開始時間為2016年1月1日，結束時間為2017年5月31日，共計517組。

2.2 數據預處理

在數據收集完成之后，還無法直接使用，原因是數據集中可能存在一些異常數據，需要對其進行處理。本文數據預處理的對象主要是針對缺失值。在污染物濃度和氣象因子監測過程中，由于監測設備故障或者網絡傳輸鏈路故障可能會造成監測數據的缺失，主要表現為數據斷檔或出現NULL值。數據缺失將破壞時間序列的連續性，進而影響預測模型的精度。因此，在建模過程中，首先要對缺失數據采用插值等方法進行數據的補足。本文主要采用多點三次樣條插值等方法補足缺失數據。

2.3 預測因子篩選

KELM預測模型能夠通過核函數很好地表示輸入向量與預測目標之間的高維非線性關系，而合適的高維輸入向量將有助于準確地描述信息特征，表達數據含義，因此KELM模型的預測能力在很大程度上依賴于輸入向量的選擇。

由于可收集的污染物和氣象因子種類較多，若全部引人會導致KELM預測模型輸入層維度過高，增加預測模型的復雜度。為此，本文借鑒文獻[13]的數據處理方法，通過相關性分析，識別出與PM2.5存在顯著相關的因子。通過將PM2.5與PM10等因子數據進行相關性分析，求其相關系數，并查閱相關系數顯著性檢驗表，找出與PM2.5顯著相關的影響因子。通過對各因子時間序列數據的分布發現，各序列均非正態分布，因此選擇計算各因子之間的Spearman相關系數，各地計算結果如表1所示。

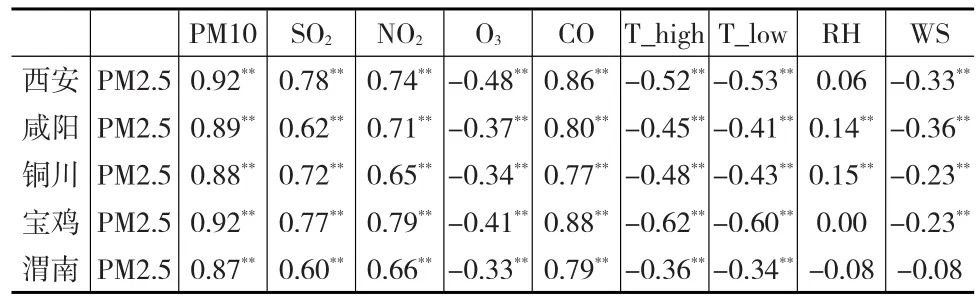
表1 相關性分析

通過Spearman相關系數計算之后就可以得到影響當地PM2.5濃度的主要因素有哪些。對各污染物數據進行分析發現，PM2.5與CO、PM10、SO2均為化石燃料燃燒的產物，而關中地區地處北方，在每年11月至3月之間會有供暖期，這期間會燃燒大量的化石燃料，因此它們均表現出春、冬季濃度較高、夏秋季濃度較低的特征，而這一點在表1中也得到了驗證，PM2.5與CO、PM10、SO2它們之間存在明顯的正相關性。SO2、NO2經二次化學反應可以形成硫酸鹽、硝酸鹽微粒，它們是PM2.5主要構成成分，因此SO2、NO2與PM2.5濃度也呈現出較強的正相關性；O3主要是在紫外線輻射作用下通過光化學反應產生，而PM2.5顆粒物濃度較高時，其消光作用散射了太陽輻射，因此O3與PM2.5呈現一定的負相關性[8]；溫度會影響氣體流動速度，當溫度較高時，空氣會加速流動，將有利于將地表的PM2.5顆粒擴散，降低地表的PM2.5濃度，因此PM2.5與T_high與T_low存在明顯的負相關性。

2.4 影響因子定階

在進行PM2.5預測時，不僅要識別與PM2.5有顯著相關關系的影響因素有哪些，還要明確各影響因素對PM2.5影響的時效性。需要根據各輸人變量與輸出變量的互相關系數確定模型中各輸人變量的延遲階數。本文這里借鑒ARDL模型中確定各影響因子滯后階數的方法，通過該方法識別出PM2.5與自身及其他相關因子之間存在最大滯后階數。經ARDL模型識別結果如表2所示。

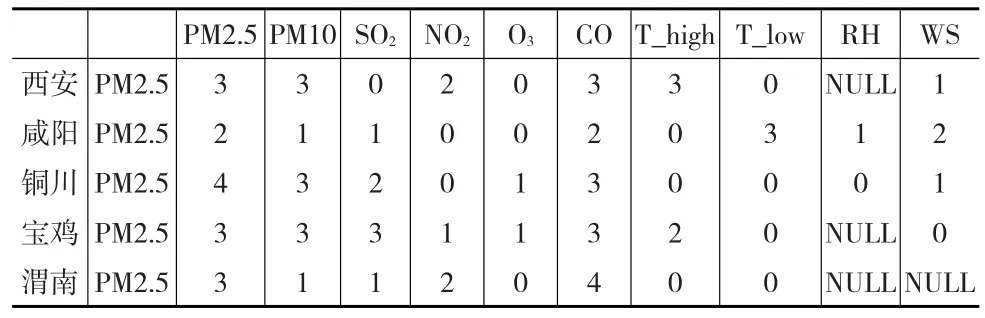
表2 滯后階數

通過檢測結果發現，在西安與PM2.5存在長期相關關系的有PM2.5、PM10、NO2、CO、T_high以及WS、它們的最大延遲階數分別為3、3、2、3、3和1。由此可以確定KELM的單隱層神經網絡結構，其輸入層的向量個數為15，其輸入深入層神經元對應的數據輸入為：PM2.5（-1）、PM2.5（-2）、PM2.5（-3）、PM10（-1），PM10（-2）、PM10（-3）、NO2（-1）、NO2（-2）、CO（-1）、CO（-2）、CO（-3）、T_high（-1）、T_high（-2）、T_high（-3）和WS（-1）。

2.5 預測結果及評價

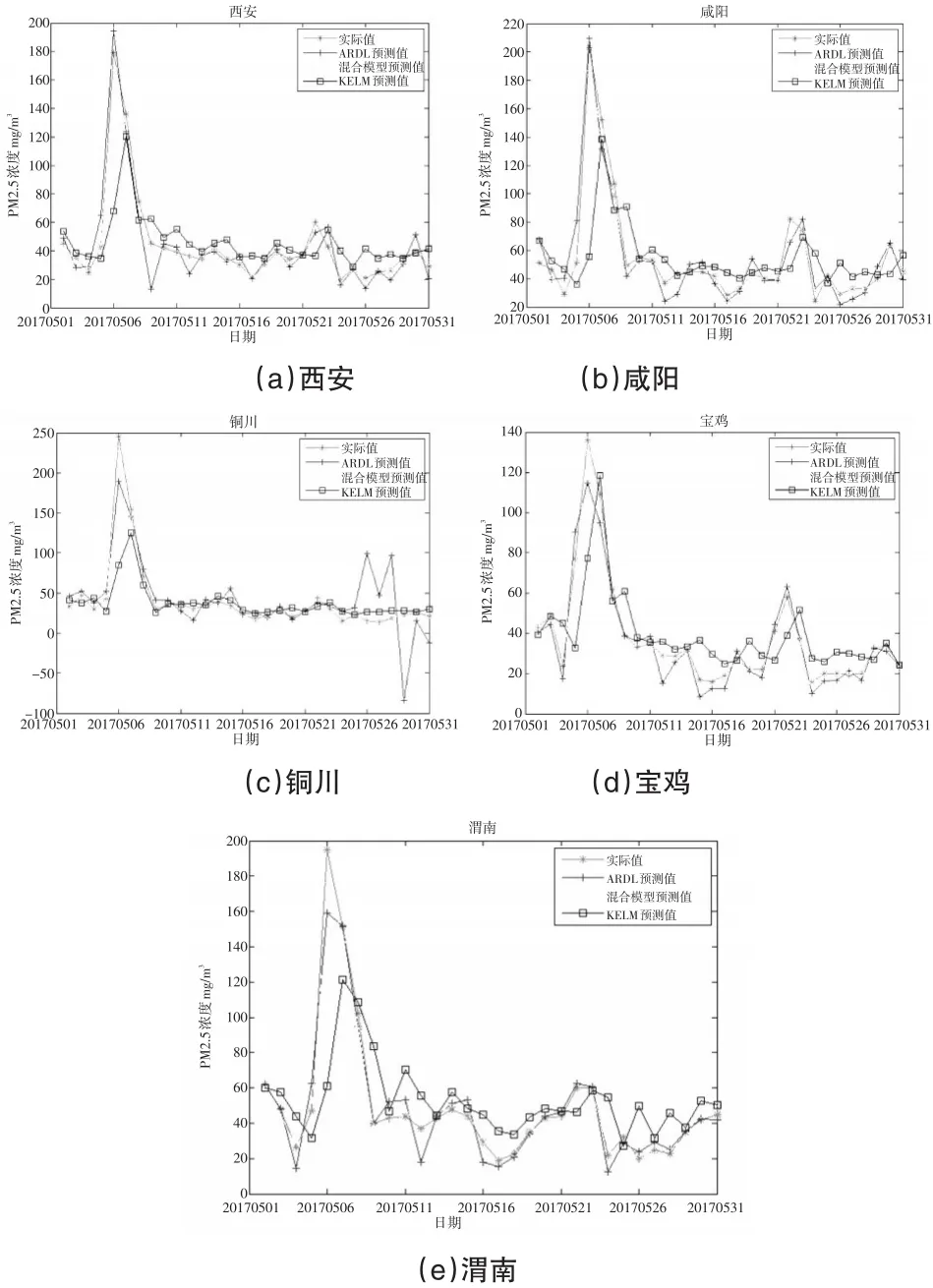
確定了KELM預測模型的各輸入數據之后，就可以使用KELM算法進行訓練與預測。由于KELM算法的適用性受到核參數的影響，因此要提高KELM的適用性就必須對核參數尋優，本文采用FFOA算法對KELM中的核參數優化。在FFOA優化過程中設置迭代次數為100，果蠅種群規模也為100。經FFOA優化后即可尋得最優核參數，并應用尋得的核參數建立KELM預測模型進行預測。為了驗證混合模型的預測效果，本文應用混合模型、ARDL模型以及KELM模型（隨機生成核參數）分別對關中地區五地市2017年5月1日至2017年5月31日的PM2.5日均濃度進行了預測，預測結果如圖1所示。

通過觀察圖1中曲線的擬合情況可以看出混合模型預測結果曲線相較于ARDL和KELM預測結果曲線更能有效跟蹤實際值曲線的變化趨勢。同時在一些極值點上，混合預測模型表現出更好的預測性能，正如圖1中所示，在2017年5月5日關中地區出現了一次極端PM2.5污染事件，五地市當日的PM2.5濃度較前一日出現明顯增加，部分地區（西安、銅川）當日濃度是前一日濃度的4～5倍。面對這種極端突變情況，混合模型表現出了較好的預測效果，當日混合模型在各地的絕對百分比誤差均保持在9%以內，其中寶雞最小為4.45%，渭南最大為8.81%，五地市絕對百分比誤差為6.8%，而ARDL與KELM分別為13.68%和62.36%，由此可以看出混合模型在應對突變情況的能力明顯優于ARDL和KELM。除此之外，混合模型預測的穩定性也明顯優于ARDL模型和KELM模型，例如在銅川地區2017年5月25日至2017年5月31日這個時間區間，ARDL模型的絕對百分比誤差最大值竟然達到561.67%，最小值也達到了41.24%，同期KELM模型的預測準確率也較差，其絕對百分比誤差最大值為86.97%，最小值也達到了29.03%，而同時間段，混合模型的絕對百分比誤差的最大值為13.68%，最小值為2.83%，由此可以看出ARDL模型與KELM模型在預測穩定性方面較混合模型有明顯差距。為了更加精確地評價各個預測模型的預測效果，使用前文中提出的3個評價指標對3個預測模型進行評價，評價結果如表3所示。

由表3可以看出，混合模型在3個評價指標上均明顯優于ARDL模型和KELM模型，說明了混合模型能夠更好地擬合PM2.5濃度數據。同時，混合模型在各地區均能得到較好的預測效果，進一步說明了混合模型的適應性強，性能穩定，能夠為政府部門應急處理突發性PM2.5污染事件提供有力的決策支持。

3 結論

（1）根據PM2.5日均濃度數據的自相關性以及與其他影響因子日均數據的延遲相關性，建立了PM2.5混合預測模型，該模型可以動態更新訓練集，確保預測模型能夠保持對新現象新規律的適應性。混合模型在與ARDL以及KELM預測模型的比較中，表現出良好的預測精度和穩定性。

表3 模型指標評價結果

（2）混合模型需要對KELM的核參數進行優化，這與ARDL以及KELM模型相比需要增加一定的計算代價。然而FFOA算法的尋優效率較高，因此總體而言本文模型增加的運行時間有限，不會對其實踐應用產生較大影響。

（3）根據實驗結果可看出本文模型對于PM2.5預測精度有明顯提高，尤其是對于極值點本文模型能更好地應對PM2.5濃度的突變情況，預測精度較高，因此可以認為PM2.5經相關性分析以及ARDL處理后，能夠識別出與PM2.5濃度具有顯著相關性的因素，有助于預測模型更好地總結規律、發現特征，提高模型的預測精度和響應能力。

（4）本文模型結構簡單，易于實現，具有一定的實用性。本文的研究結果不僅能有效應用于地區日均PM2.5濃度預測，同時也可用于小時或其他時間維度的PM2.5濃度預測，可以為政府開展空氣污染預警、城市綜合管理提供理論支持和決策依據。