中國中產階層比重的測度及變遷研究

張曉華，紀 宏

（1.首都經濟貿易大學 統計學院，北京 100070；2.鄭州大學西亞斯國際學院 商學院，鄭州 450000）

0 引言

中國社會要發展成為一個可持續發展的、穩定的“橄欖型”現代社會,需要培育龐大的社會中間力量，這個中間力量即中產階層，然而，中產階層規模有多大？發展現狀到底如何？變化趨勢怎樣？這一系列問題都值得研究。國內外學者對中產階層已經有了比較全面深入的研究，經濟學界常從收入指標入手，社會學界常輔助問卷調查數據從多指標研究中產階層。本文將在前人學者的研究基礎上綜合宏觀、微觀數據對以恩格爾系數單個指標界定的中產階層的現狀進行描述性統計分析，并對其比重進行測度，最后研究中產階層的變遷趨勢，從而找出中產階層發展的規律，對于完善中產階層的研究，穩定社會、實現共同富裕、全面建設小康社會具有重要的意義。

1 概念的界定和數據說明

1.1 中產階層概念的界定

通過對國外相關文獻的研究發現，國外一般將中產階級、中間階層和中產階層等概念與中等收入群體的概念等同，普遍使用Middle Class。國內學者對“中產”概念進行界定時有兩種方式，一種是回避對“中產”概念的明確界定；另一種是對“中產”做一個描述性的分類說明。但所有學者都認為“中產”與職業關系密切，且大多以收入、財產或消費指標來定義中產。本文認為概念的界定首先要服從研究者的目的且能做定量分析，其次要充分考慮概念賴以存在的基本理論基礎和社會現實基礎，最后，鑒于收入可能會受到概念界定的不統一、調查難度、地域收入消費水平的差異、經濟周期，“財不露富”的心理作用、被調查者回答的模糊和避諱、地下經濟和隱形收入的存在等多種因素的影響,因此，本文選擇較容易準確測定的消費指標來界定中產階層，且消費方式能夠更加系統地體現出一個人的生活習慣及生活品質。

消費指標中常用的是恩格爾系數，考慮到中國還處于社會轉型階段，加上居民自身的生活習慣、經濟制度和保障等因素，本文將恩格爾系數進行修正以界定中產階層的標準。本文選擇將國際標準的恩格爾系數減去0.1，即恩格爾系數在0.3～0.4之間來界定出我國的中產階層。

1.2 數據說明

本文的數據從兩方面來考慮，一是采用宏觀層面中國統計年鑒上的數據，包括城鎮、農村、七分組或五分組數據。二是采用微觀層面中國綜合社會調查（Chinese General Social Survey，CGSS）已公布的最新數據，包括2015年社會綜合調查數據和2010年社會綜合調查數據（恩格爾系數的數據在CGSS數據中僅這兩年有統計），且由于學生人口自身職業、收入乃至消費行為的不確定性，很難作為劃分中產階層的有力依據,因此，本文選取CGSS綜合社會調查中16～70歲的非學生群體這一部分具有統計分析價值的適齡社會人口的樣本數據。有效問卷數分別為8250例（2015年）和10510例（2010年）。

2 中產階層的現狀分析

2018年1月，國家統計局局長寧吉喆指出，我國消費結構中有一個很重要的變化是恩格爾系數從2016年的30.1%降到2017年的29.3%，說明居民生活水平大幅提高。考慮近幾年我國恩格爾系數，無論是全國還是城市、農村，恩格爾系數都在30%～40%之間，若這樣認為我國全民屬于恩格爾系數界定的中產階層，顯然也不太合理，但是否能從某些方面認為中產階層比重在擴大。

綜合2015年微觀CGSS調查數據來看（見下頁表1），2014年我國適齡社會人口的恩格爾系數在30%～40%之間，已經達到了小康水平。中位數的值低于平均值，說明社會消費構成右偏，標準差低于平均值且其自身數值也很小，說明數據離散程度低，恩格爾系數較為集中，消費行為相似。按照本文中產階層的界定標準，我國消費中產的比重達到了18.22%，相較于2009年的17.97%，恩格爾系數和中產階層的比重都略有增加。由于消費水平存在地區差異，進一步按照發達地區、較發達地區和欠發達地區三個區域來統計恩格爾系數，可以看出，2014年發達地區均值降低，且中產階層比重顯著降低，說明發達地區生活質量更好，貧富差距拉大，欠發達地區恩格爾系數均值顯著降低，中產階層比重增加，說明欠發達地區居民生活水平得到改善。

表1 恩格爾系數統計表 （單位：%）

3 中產階層比重的測度

首先構造衡量中產階層的恩格爾系數的密度函數，其次用核密度函數對其進行估計，得到恩格爾系數的核密度函數，然后界定衡量中產階層的恩格爾系數的上下限0.3～0.4，最后對核密度函數做數值積分求出中產階層的比重。

3.1 測度模型

核密度估計是用來估計未知密度函數的一種方法，屬于現代非參數檢驗方法之一。若f（x）是一維總體的密度函數，設K（·）是R上一個給定的Borel可測函數,hn＞0是一個與n有關的常數，滿足，定義：

但式（12）中有未知量f（x），本文采用 Sliverman（1986）提出的經驗法則，即假定f（x）為正態密度函數N（0,σ2），選取高斯核，則最優帶寬為：

最終，一維度核密度函數為：

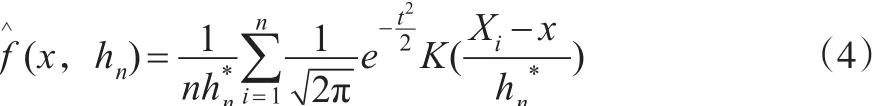
3.2 中產階層的比重

根據2015CGSS和2010CGSS數據計算出2014年和2009年的恩格爾系數，用R軟件畫出其核密度圖1。從圖1中可以看出我國多數人群恩格爾系數在0.3左右。核密度圖也呈現略微右偏的形狀，說明食物消費支出大的人群比重相對較小，人們生活水平差異大。2014年相較2009年核密度曲線表現出以下特點：曲線向右略微平移，說明居民的食物支出水平提升，家庭生活水平略微降低；曲線峰值略高，頂部上升，寬度略微減小，說明收入恩格爾系數差距縮小，中產階層比重略微增加。進一步地類似于上面的方法用R軟件畫出2014年、2009年城鎮、農村這兩年的家庭總收入核密度圖以及2014年和2009年發達地區、較發達地區和欠發達地區的家庭總收入核密度圖，得到的結論是：2014年城鎮家庭恩格爾系數相較于2009年位置變化不大，農村家庭恩格爾系數明顯右側移動，說明農村家庭生活水平質量下降。發達地區核密度圖2014年較2009年寬度變寬，較發達地區變化基本不變，欠發達地區整體右側移動，說明發達地區生活水平質量拉大，較發達地區基本沒有變化，欠發達地區人們生活水平變差。

圖1 2009年、2014年家庭恩格爾系數

結合上文給出的消費界定的中產階層的上下限標準，即恩格爾系數在0.3～0.4之間，可以得到中產階層的比重如表2所示。可以看出，2014年較2009年全國中產階層比重略微增加，城市中產階層比重略微減少，發達地區中產階層的比重也有降低。其原因或許跟經濟增長、收入變化的變動有關，也跟城市、發達地區人們有住房、消費等較大壓力有關。

表2 中產階層的比重 （單位：%）

4 中產階層的變遷分析

函數型數據的分析方法是將每一個樣本觀測看成是一個整體來考慮，且在經濟函數型數據分析中，學者們常需要找感興趣的變量隨時間變化的主要變異方式，同時又想知道多少個這樣的變化方式或形態可以較好地擬合原始曲線樣本，即需要通過確定曲線數據的典型函數特征探討數據變異的主要成分。主成分分析就能很好地解決這種問題，本文要研究恩格爾系數構成的中產階層的變化規律，從時間上去看中產階層的變遷趨勢，所以把函數型數據主成分法引入到此。且由于微觀數據的不充分（只有兩年的數據），不足以表示近幾年中產階層的變遷情況，本文采用國家統計局公布的城鎮七分組數據和農村五分組數據將函數型數據的基展開和函數型主成分分析的方法引入中產階層的變遷分析之中。

4.1 函數型數據的基展開

本文采用B樣條基將離散的數據轉化為函數。假定基函數f（xi）是樣條函數，一個有k個結點的三次樣條函數可以由b1（x1）,b2（x2）,b3（x3），…，bk+3（xi）的線性組合構成，其中，bi（xi）有多種選法，本文選用三次多項式為基礎，然后在每個結點添加一個截斷冪基，即：

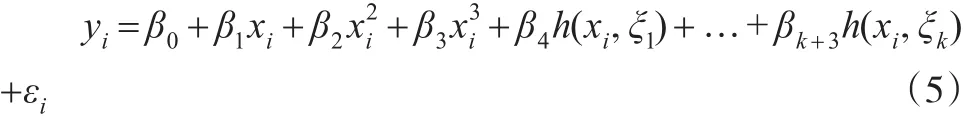
其中，h（x,ξ）=（x-ξ）3,（x＞ξ），h（x,ξ）=0,（x＜ξ）。ξ是結點，估計模型時,采用最小二乘法估計k+4個系數。

4.2 函數型主成分分析

4.2.1 函數型主成分的數學模型

經典的多元統計分析中是要找特征向量。在函數性數據主成分分析中，這個特征向量是一個變動的函數，叫主成分權函數，記為ξ（s），其中s在一個區間T中變化，且ξ（s）平方可積。

第j個函數主成分，其權函數ξj（s）滿足如下數學模型的條件：

其中，zij= ∫Tξj（t）xi（t）dt為第i個樣品的第j主成分得分，i=1,2,…,N。且求得的諸多權函數ξj（s）滿足標準正交約束條件，即：

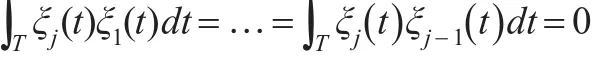
本文將這K個正交的權函數ξk（s），k=1,2,…,K，作為基函數。

4.2.2 函數型主成分的求解方法

在多元統計分析中，求解主成分是要尋求協方差陣或相關系數陣的特征值和特征向量。在函數型主成分分析中是要求解Vξ=ρξ這個特征方程和和對應的特征函數。

（1）求解特征方程

若令p×p階矩陣V=N-1X"X，即V表示樣本方差—協差陣，類似于多元統計分析，求解函數性主成分權函數ξj（s）轉化為解如下的特征方程：其 中 ，設xi（s）和xi（t）的 協 方 差 函 數 為ν（ ）s，t，s，t∈T，即：

若定義一個算子：

即V是權函數ξ的一個積分變換，并稱其為協方差算子。因此式（7）的特征方程式可表述為Vξ=ρξ（注意這里的ξ是特征函數，不是特征向量）。

（2）離散化法求解權函數

設觀測xi（t）的時點t1，t2，…，tn均等地分布于區間T，即在區間T的n等分點上取值，這樣可得到多元數據集X：

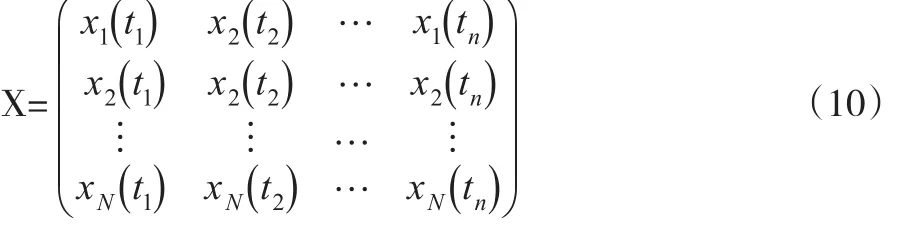
類似多元統計分析，可求出滿足式（11）的特征值和特征向量：

其中，u為n維向量。

樣本方差-協差矩陣V=N-1X"X的元素為ν（tjl,tk）。對于給定的函數ξ，令ξ?是由ξ（tj）構成的n維列向量，l是區間T的長度，w=l/n。于是，對于任意的tj有：

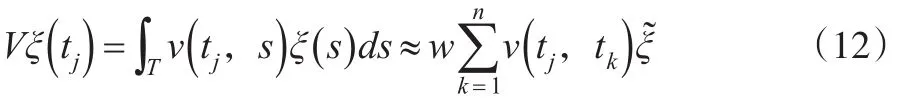
因此，函數性特征方程Vξ=ρξ有近似離散形式：

這個方程的解將對應于Vξ=ρξ式的解，特征值之間的關系ρ=wλ。標準化約束的近似離散形式是因此如果向量u是矩陣V的標準化特征向量，則ξ?=w-1/2u。在得到ξ?后，使用任何簡便的插值法便可從離散值ξ?獲得近似特征函數ξ。

4.3 中產階層變遷的數據分析

由于2013年前后數據口徑有很大的變化，且城鎮七分組數據和農村五分組數據只在2013年前統計，因此本文采用的數據是《統計年鑒（2002—2013）》中計算出的恩格爾系數進行中產階層變遷的分析。

4.3.1 恩格爾系數分組數據基展開

本文采用R軟件選取B-樣條基展開，將七分組城鎮恩格爾系數數據及其變動率繪制修勻曲線。結論是：除最低收入組的恩格爾系數的波動相對大點外，其他六組恩格爾系數雖一直有小幅波動，但總體上保持平穩的發展。衡量中產階層群體的中間三條曲線（中下組、中等組和中上組）的恩格爾系數變動率波動特征一致，都是周期性的先增后減，且在2004年、2008年恩格爾系數達到增幅最大，2012年后有下降的趨勢。同樣的，根據五分組農村恩格爾系數和其變動率也做B-樣條修勻處理，結論是：農村五分組曲線比城鎮七分組曲線變動劇烈，并且整體波動趨勢下降。在2004年達到最高點，原因可能是2004年物價飛漲，但收入并沒有相應的增加，且中間三條曲線即衡量中產階層的群體自2012年后有下降的趨勢，說明農村中產階層人群近幾年來生活水平在提高。但從農村恩格爾系數變動率五分組數據來看，除低收入組變動率在接近2012年變動異常低外，其他組波動率基本一致。

4.3.2 恩格爾系數分組數據函數性主成分分析

進一步地，采用R軟件分別做七分組城鎮恩格爾系數變動率和五分組農村恩格爾系數變動率的主成分偏離均值的效果圖。從圖2和圖3可以看出，無論是城鎮恩格爾系數還是農村恩格爾系數都是第一主成分偏離均值較多，波動較大，并且解釋了函數的大部分變動。并且第一主成分都是2006年以前和2010年后導致五分組恩格爾系數大幅變動。事實上，2006年、2010年國家一系列惠民政策的出臺，增加了人們的收入，相應的增加了消費支出，因此在各項政策的管控下，五分組恩格爾系數產生了變動。

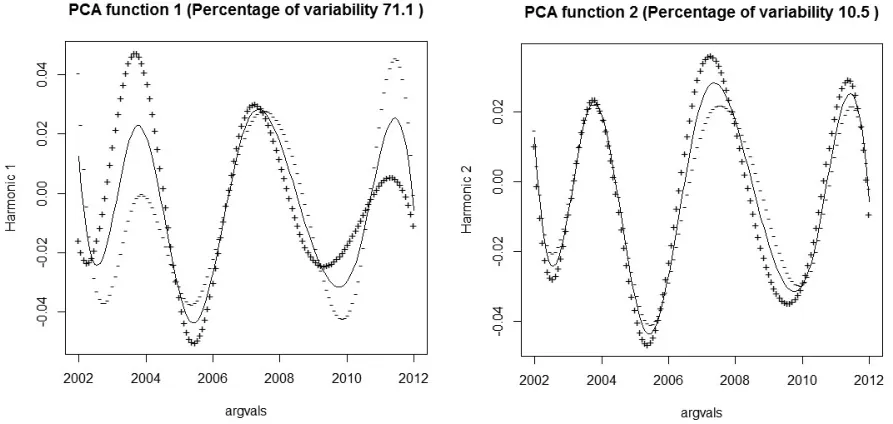
圖2七分組城鎮恩格爾系數變動率的主成分偏離均值的效果圖

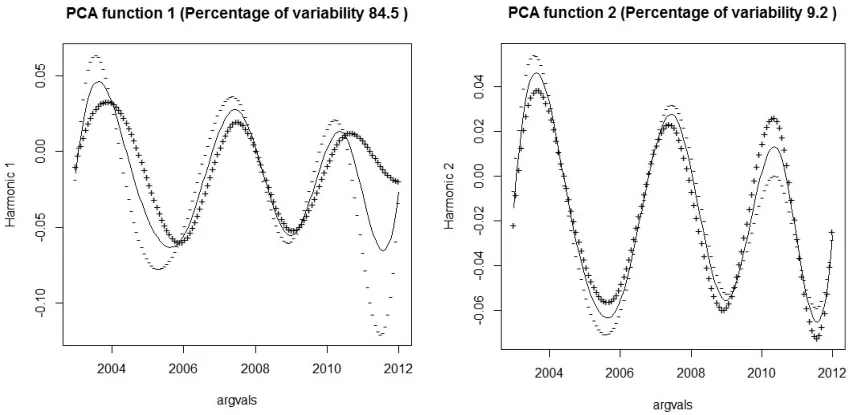
圖3五分組農村恩格爾系數變動率的主成分偏離均值的效果圖

5 結論

恩格爾系數界定的中產階層群體密度函數略微呈現右偏分布，說明人們生活水平差異明顯。2014年相較2009年，人們生活水平質量下降，但差異縮小。從城鄉來看，城鎮恩格爾系數變化不大，農村右移明顯，說明農村生活質量下降。從地區來看，說明發達地區生活水平質量拉大，較發達地區基本沒有變化，欠發達地區人們生活水平變差。總體來說，中國中產階層比重規模不大，但整體有增加的趨勢。

函數型數據分析的結果顯示：中產階層群體恩格爾系數曲線波動特征一致，都是周期性的先增后減，且2012年后有下降的趨勢，說明各收入組人們的食物支出在減少，生活水平有提高。城鎮恩格爾系數波動率的修勻曲線波動大致相同，但農村恩格爾系數曲線相較城鎮變動劇烈，從恩格爾系數主成分偏離均值的效果圖可以看出，無論是城鎮還是農村都是2006年以前和2010年后導致恩格爾系數大幅變動。

總之，我國中產階層雖然比重大致都在增加，但規模不大，與歐美等發達國家中產階層的比重相比仍有較大差距，但人們生活質量確實得到提高，因此“擴中”的任務仍很艱巨。