科技評價中因子分析信息損失的改進

俞立平，郭強華，張再杰

（1.浙江工商大學 統計與數學學院，杭州310018；2.云南大學 經濟學院，昆明 650504；3.貴州財經大學 中國西部綠色發展戰略研究院，貴陽 550025）

0 引言

因子分析是Spearman（1904）[1]提出的一種重要的客觀評價方法，具有能夠處理大量多指標數據、便于提取少數公共因子等優點，因此在科技評價中的應用越來越廣泛。在中國知網中，查篇名“因子分析”的論文高達9000篇，而主題包括“因子分析”+“科技”的論文有1200多篇，包含“因子分析”+“期刊”的論文有200多篇。其他還有許多涉及采用因子分析的大學評價、學科評價、機構評價的論文。

因子分析評價也存在一些不足。在因子分析評價中，一般采用SPSS軟件進行，通過降維將眾多指標精簡為少數關鍵因子，然后對這些因子按照方差貢獻率大小進行賦權，最后進行加權匯總即得到評價總分，通常情況下需要累計方差貢獻率大于85%，不過在實際應用中可以接受的方差貢獻率在80%左右即可。因子分析方法評價有三個問題：第一，在科技評價中，往往采用2～4個關鍵因子進行評價，目前的實證論文中，累計方差貢獻率很少超過90%，那么剩下的其他因子就被省略掉了，存在著較大的信息損失，這是不合理的。第二，在評價對象眾多的情況下，區分度會很低，評價時是否舍棄其他公共因子對評價結果影響較大，對于增加其他公共因子能夠得到排名改善的評價對象而言，會認為評價不夠公平。第三，在計算機技術日益發達的今天，如果說降維作用不可忽視外，那么省略其他因子精簡計算根本就沒有必要。以上三個問題的根源主要還是因子分析評價對原始數據信息的遺棄。對因子分析評價存在的問題進行深入分析，不僅可以優化因子分析方法，深化對其應用的理解，豐富因子分析理論，而且在實際應用中也便于對因子分析方法的選擇，提高評價的科學性、適用性和公眾接受程度。

在科技評價中，因子分析涉及范圍非常廣泛，絕大多數領域均有采用因子分析的研究文獻。李子倫（2014）[2]從產業體系的科技創新能力、人力資本積累水平與資源利用效率水平三個方面建立指標體系，采用因子分析對金磚國家產業結構升級水平進行評價。顧雪松等（2010）[3]從科技投入、科技產出、科技對經濟與社會的影響三個方面選取科學技術評價指標，利用R聚類與因子分析相結合的方法定量篩選指標，構建了科學技術綜合評價指標體系。董曄璐（2015）[4]運用因子分析法對我國31個省份的高校科技創新能力進行分析與評價。黃斌等（2013）[5]運用因子分析模型對江蘇省13個地級市的科技服務業競爭力進行評價。夏文莉（2013）[6]通過因子分析法分析了科研學術不端行為的有關要素，認為科研誠信和科技評價緊密相關。

學術期刊評價中因子分析也得到了廣泛的應用。吳濤等（2015）[7]采用6個文獻計量指標，通過對WoS數據庫和Scopus數據庫共有的1881種醫學進行評價，尋找公共因子。鄭麗霞（2014）[8]選取2014年湯森路透社JCR中SCI收錄的20種期刊數據為樣本，采用因子分析法對其8個評價指標進行綜合評價。賀穎（2007）[9]采用因予分析的方法，尋求管理類學術期刊引文的基本特點和一般規律，同時透視管理類期刊的學術水平和期刊質量及其學術影響力。柴玉婷和溫學兵（2016）[10]以2015版中國科技期刊引證報告（擴刊版）中的14個量化評價指標為依托，利用因子分析法對42所師范大學理科學報的學術影響力進行分析排名。劉巖（2016）[11]利用多維面板數據，采用因子分析法對中國圖書情報學19種核心期刊的發展態勢進行了研究。何莉等（2014）[12]采用11個文獻計量指標，運用因子分析法，對安徽省高校自然科學學報的學術影響力水平進行綜合評價。

關于因子分析方法應用的注意事項與存在的問題，MacCallum等（1999）[13]探討了不同樣本大小及不同變量公共方差情況下，所得的因子負載的精確程度，認為因子分析在大樣本下應用更好。Fabrigar等（1999）[14]認為因子分析中每個因子至少應包含4個或是更多的變量才能確保因子被有效識別，指標數量不能太少。Edward（1992）[15]認為因子分析與主成分分析的前提條件是數據必須服從正態分布，而實踐中這種條件很難具備。林海明（2006）[16]從找因子分析精確解的角度，以主成分分析理論為基礎，應用矩陣運算方法，建立了新的因子分析模型，消除了理論假設的誤差，給出了因子分析模型的精確解，找到了因子分析與主成份分析的關系式。熊國經等（2016）[17]認為采用多屬性評價方法評價學術期刊會遇到指標間多重共線性以及指標權重不確定的影響，采用因子分析確定關鍵因子，采用熵權法確定權重，最后用加權TOPSIS進行評價。俞立平和劉愛軍（2014）[18]根據因子分析隱含的假設是評價指標必須服從正態分布的原理，認為在期刊評價指標普遍呈冪律分布的情況下，最好將評價指標取對數后再進行評價，否則會擴大系統誤差。靖飛和俞立平（2012）[19]針對因子分析和主成分分析在期刊評價中存在的問題，提出了一種新的學術期刊評價方法——因子理想解法，首先采用因子分析篩選出關鍵因子，然后確定各關鍵因子的權重，在此基礎上將關鍵因子標準化后采用加權TOPSIS進行評價。

從現有的研究看，因子分析在科研機構評價、大學評價、學術期刊評價、科研人員評價等科技評價中得到了廣泛應用，是迄今為止應用較多、影響較廣的客觀評價方法之一。關于因子分析評價的適用條件、評價方法可能存在的問題，現有的研究總體不多，有待進行深入。本文在對因子分析存在問題分析的基礎上，提出了一種新的評價方法——完全信息因子分析法，并以JCR經濟學期刊為例，比較采用傳統因子分析評價與完全信息因子分析評價結果的區別。

1 因子分析評價存在的問題及改進

1.1 因子分析方法評價存在的問題

1.1.1 科技評價方法的分類

在科技評價中，根據評價數據的確定性情況，宏觀上有兩大類評價方法（見圖1）。第一大類是確定性評價方法，從信息完全度角度，又包括兩類，一類是完全信息評價方法，大多數評價方法均是如此，比如層次分析法（AHP）、理想解法（TOPSIS）、熵權法、灰色關聯法等，其特點是盡管評價方法不同，但是評價結果嚴格反映評價指標數據的信息。另一類是不完全信息評價方法，如因子分析、主成分分析、粗糙集等，其特點是評價結果只反映了評價指標的大部分信息，主成分分析和因子分析均采用特征根大于1的主成分或主因子來進行評價，粗糙集則干脆通過約簡進行了指標精簡，刪除了一些指標。第二大類評價方法稱為模糊性評價方法，又包括指標數據模糊或權重數據模糊兩類。當然這并不是本文重點關注的范疇，因為在科技評價中，絕大多數評價是確定性評價方法，本文重點分析確定性評價中因子分析方法存在的問題。

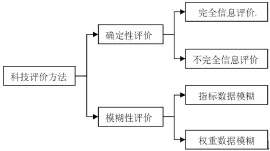
圖1評價方法分類

1.1.2 因子分析方法評價的優點

在科技評價中，從因子分析方法的優點分析入手，可以分析不完全信息的原因，在此基礎上進行改進。

第一，因子分析方法是一種客觀評價方法。在科技評價中，如果采用主觀方法確定權重，則重復性往往較差，換一批專家權重設定肯定不一致，當然評價結果也不一致，這導致許多詬病，認為主觀評價方法不公平，而客觀評價方法不需要設定指標權重，完全根據客觀數據來評價，如果數據確定，結果就確定，減少了人為因素干擾評價結果的可能，因此有一定的價值。

第二，因子分析方法能夠降維。因子分析通過數十甚至上百個評價指標的處理，能將其降維為少數公共因子，這少數公共因子中包括了原始數據的大量信息，而且可以在現實世界中對其命名，化繁為簡，便于總結提煉。在指標眾多的情況下，單靠人的大腦對指標分類是非常困難的，何況有些評價指標具有多重含義，比如即年指標，既可以用來表示期刊影響力，也可以用來表示期刊的時效性，究竟將其歸為哪一類？

第三，因子分析提取的公共因子不相關。這一點是因子分析的又一個重要優點，在技術經濟分析中，變量之間的相關容易造成多重共線性，因子分析徹底解決了這一問題，而且每個因子均具有經濟含義，這是非常了不起的算法。

第四，因子分析方便計算，運用SPSS軟件，將處理好的數據導入，短短數分鐘可以得到評價結果，這是許多其他評價方法難以做到的。

1.1.3 因子分析方法評價存在的問題

以上四個優點是因子分析法得到廣泛運用的原因，但是因子分析方法也帶來了新的問題：

第一，客觀評價一定就沒有問題嗎？雖然客觀評價方法優點眾多，但是如果評價不能體現出管理者的意志，評價不能為管理服務，那么這種評價又有什么意義？比如科技創新評價中，研發投入是最重要的指標，但哪種客觀評價方法怎么能保證該指標最重要？雖然因子分析方法中回避了直接權重的概念，但采用俞立平等（2010）[20]提出的模擬權重計算方法，將因子分析評價結果與評價指標進行回歸，對回歸系數進行標準化就可以得到各評價指標的模擬權重。這樣因子分析作為客觀評價方法不需要人工賦權的優點就要打折扣，因為它不能保證評價為管理服務，不能保重關鍵指標的重要性。

第二，因子分析方法丟失了原始數據的大量信息。由于因子分析方法評價時只采用少數公共因子進行評價，這樣其他因子中的大量信息就會舍棄。這種處理方法是值得商榷的，從信息量看，少數公共因子基本能夠解釋所有數據信息量的80%以上，總體上似乎沒有問題，但對評價個體就不同了，在評價對象眾多、區分度較低的情況下，是否舍棄其他不重要的公共因子對評價結果就會產生較大的影響。比如在大學評價中，采用因子分析對全世界大學進行排名，采用少數公共因子和采用全部公共因子評價大學排名肯定會有較大不同。

降維是因子分析的最大優點，但是降維的目的是為了便于分析，不一定是為了評價，或者說，為了對數據進行更為精準的分析，可以采用因子分析方法進行降維，但不一定要采用因子分析進行評價。根據以上分析，因子分析適合降維這是無可爭議的，但是因子分析未必就適合評價。

第三，精簡計算在現代是沒有意義的。降維可以精簡計算這是肯定的，盡管提取公共因子的過程略顯繁瑣，但通過SPSS軟件非常方便。采用少數公共因子評價與采用全部公共因子評價增加的計算量可以忽略不計。在科技評價中，隨著計算機技術、軟件技術日趨成熟，加上大數據、云計算等新一代信息技術的普及，已經沒有必要考慮科技評價的算法了，最重要的是評價方法是否科學、合理、合適、公平。

第四，因子分析并沒有降低評價成本。有些不完全信息評價方法是有其存在意義的，比如說粗糙集，評價指標個數眾多必然意味著評價成本增加，在這種情況下，通過指標約簡雖然犧牲了部分信息，但是大大降低了評價指標數量，節約了評價成本。但是因子分析方法通過降維并沒有減少評價指標，當然也沒有降低評價成本，因此不能從節省成本的角度肯定因子分析方法。

1.2 完全信息因子分析法

所謂完全信息因子分析（All Information Factor Analysis，AIFA），就是在因子分析評價中，采用全部公共因子進行評價，而不是少數幾個公共因子。這樣做法的最大好處是：

第一，一點也不犧牲原始數據信息，做到了評價方法的公平公正，容易被公眾所接受。

第二，計算簡單，可以繼續基于SPSS軟件進行，不同的是在提取公共因子時采用全部可能的公共因子，也就是說公共因子的數量與評價指標的數量是一樣的。

第三，并不影響因子分析的其他優點。比如降維，在評價過程中，同樣可以通過降維找到少數幾個公共因子，計算方差貢獻率，分析哪些指標對評價影響較大等等，只不過不采用少數幾個公共因子評價而已。

1.3 最大信息因子分析法

在因子分析中，根據方差貢獻率設定權重不一定是可取的，雖然這種權重確定方法本質上是一種客觀賦權法，完全根據數據說話，但不一定就是最有效的賦權方法。因子分析中因子的權重取決于相關指標的數量，比如期刊評價，如果影響力指標較多，時效性指標較少，那么第一因子肯定是影響力，權重最高，第二因子就是時效性，權重要低一些。假設我們現在評價的目的主要是評價期刊的學術活力，那么影響力指標的權重必須低于時效性指標，所以客觀賦權就不一定合理了。

采用因子分析提取公共因子個數的上限是由評價指標的數量決定的，但是如果從對公共因子命名、具有經濟含義的角度，公共因子的數量又是有限的。究竟如何選取，可以設置最大公共因子后根據旋轉矩陣來進行判定，此時得到的可以解釋的公共因子數量往往比傳統因子分析評價多，但肯定少于所有公共因子數量，可以將這種采用可解釋公共因子進行評價的方法稱為最大信息因子分析法（Maximum Information Factor Analysis，MIFA）。權重設定不必采用方差貢獻率，可以通過專家會議法等主觀評價方法確定。

根據最大信息因子分析法獲得所有的可解釋和命名的公共因子后，由于這些公共因子互不相關，因此便于專家進行賦權，然后進行加權匯總，這樣不僅最大限度地保留了原始數據的信息，而且體現了評價的管理目的，具有較強的實踐意義。

2 評價實證

2.1 數據來源與評價指標設計

為了比較因子分析評價、完全信息因子分析評價、最大信息因子分析評價的區別，本文以JCR 2015經濟學期刊評價為例進行分析。2015年JCR經濟學期刊共有333種，數據量較大，便于因子分析。JCR評價指標共有11個，分別是：總被引頻次（Z1）、影響因子（Z2）、他引影響因子（Z3）、5年影響因子（Z4）、即年指標（Z5）、特征因子分值（Z6）、論文影響分值（Z7）、標準化特征因子（Z8）、被引半衰期（Z9）、引用半衰期（Z10）、影響因子百分位（Z11）。

由于部分期刊評價指標數據缺失，原因包括期刊辦刊年度較短、0引用等，需要進行數據清洗，經處理后還有278種期刊，指標數據描述統計如表1所示。

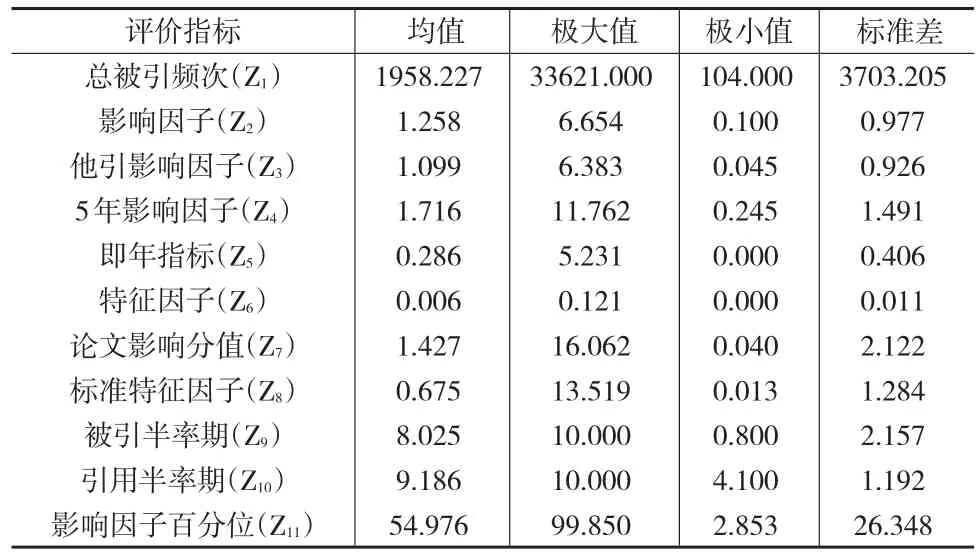
表1 指標描述統計

2.2 實證結果

2.2.1 因子分析法評價的旋轉矩陣與載荷分析

首先采用因子分析法進行評價，KMO檢驗值為0.839，bartlett檢驗值為7933.350，相伴概率為0.000，說明適合采用因子分析方法進行評價。旋轉矩陣如表2所示，特征根大于1的共有兩個公共因子，第一公共因子的方差貢獻率為56.95%，第二公共因子的方差貢獻率為17.37%，合計74.32%。除了即年指標Z5、被引半衰期Z9、引用半衰期Z10屬于第二公共因子外，其他指標均屬于第一公共因子，所以第一公共因子可以命名為期刊影響力因子，第二公共因子可以命名為期刊時效因子。

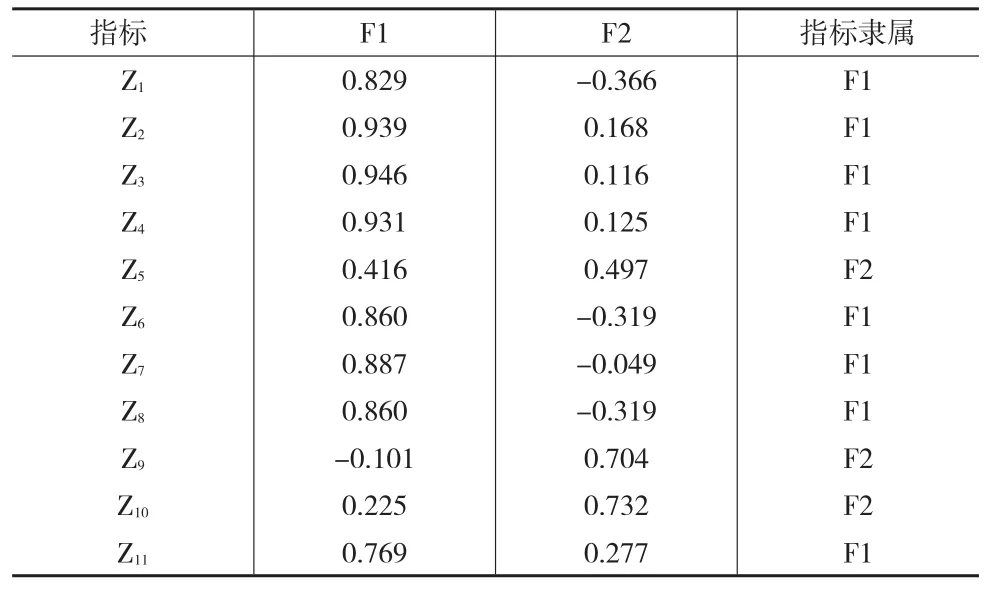
表2 因子分析旋轉矩陣

2.2.2 完全信息因子分析法評價的旋轉矩陣與載荷分析

下面采用完全信息因子分析法進行評價。由于采用完全信息，所以在提取公共因子時，采取可能極大值原則，11個評價指標選取11個公共因子，旋轉矩陣如表3所示。雖然提取了11個公共因子，但是所有指標只能歸到5個公共因子中，第一公共因子包括影響因子Z2、他引影響因子Z3、5年影響因子Z4、論文影響分值Z7、影響因子百分位Z11，可以將其命名為影響因子類指標；第二公共因子包括總被引頻次Z1、特征因子Z6、標準特征因子Z8三個指標，可以將其命名為期刊總體影響力指標；第三公共因子是即年指標Z5，為當年時效性指標；第四公共因子是引用半衰期Z10；第五公共因子是被引半衰期Z9。

表3 完全信息因子分析旋轉矩陣

從平方載荷旋轉旋轉和看（表4），前5個因子的累計方差貢獻率為91.47%。后幾個因子的方差貢獻率很小，F11幾乎為0，F10僅為0.098%，F9僅為0.487%，F8僅為0.848%，均不到1%。當然在具體評價時，為了保持原始數據信息的完整性，全部納入進行評價。

表4 平方載荷旋轉和

2.2.3 兩種方法評價結果比較

因子分析與完全信息因子分析的評價結果如表5所示，由于期刊較多，僅列出了因子分析排名前30的期刊。兩種評價方法的評價結果相差較大，排名前30的期刊區分度本來就大，正常情況下應該具有一定的評價魯棒性，即評價方法的差異不會帶來評價結果排序的較大變化，但在實際情況下并非如此。

表5 評價結果比較

因子分析評價與完全信息因子分析評價的散點圖如下頁圖2所示，很明顯可以看出兩者正相關，通過相關系數分析發現，兩者的相關系數為0.866，并且通過了統計檢驗，具有較高的相關度。但是相關度較高是從總體分析的，對于個體而言，兩種評價方法評價結果還是相差較大的。

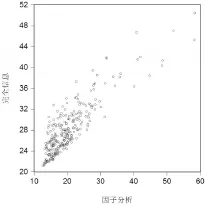
圖2完全信息因子分析與因子分析評價結果對比

2.2.4 最大信息因子分析法評價

從完全信息因子分析的旋轉矩陣看，11個評價指標中共提取了5個公共因子，本文以這5個公共因子為基礎采用最大信息因子分析法進行評價，為了和完全信息因子分析評價結果進行比較，這里繼續采用方差貢獻率賦權，評價結果如表6所示。同樣給出前30種期刊，可以很明顯看出，盡管評價結果排序有所區別，但是評價結果排序的一致性較高。

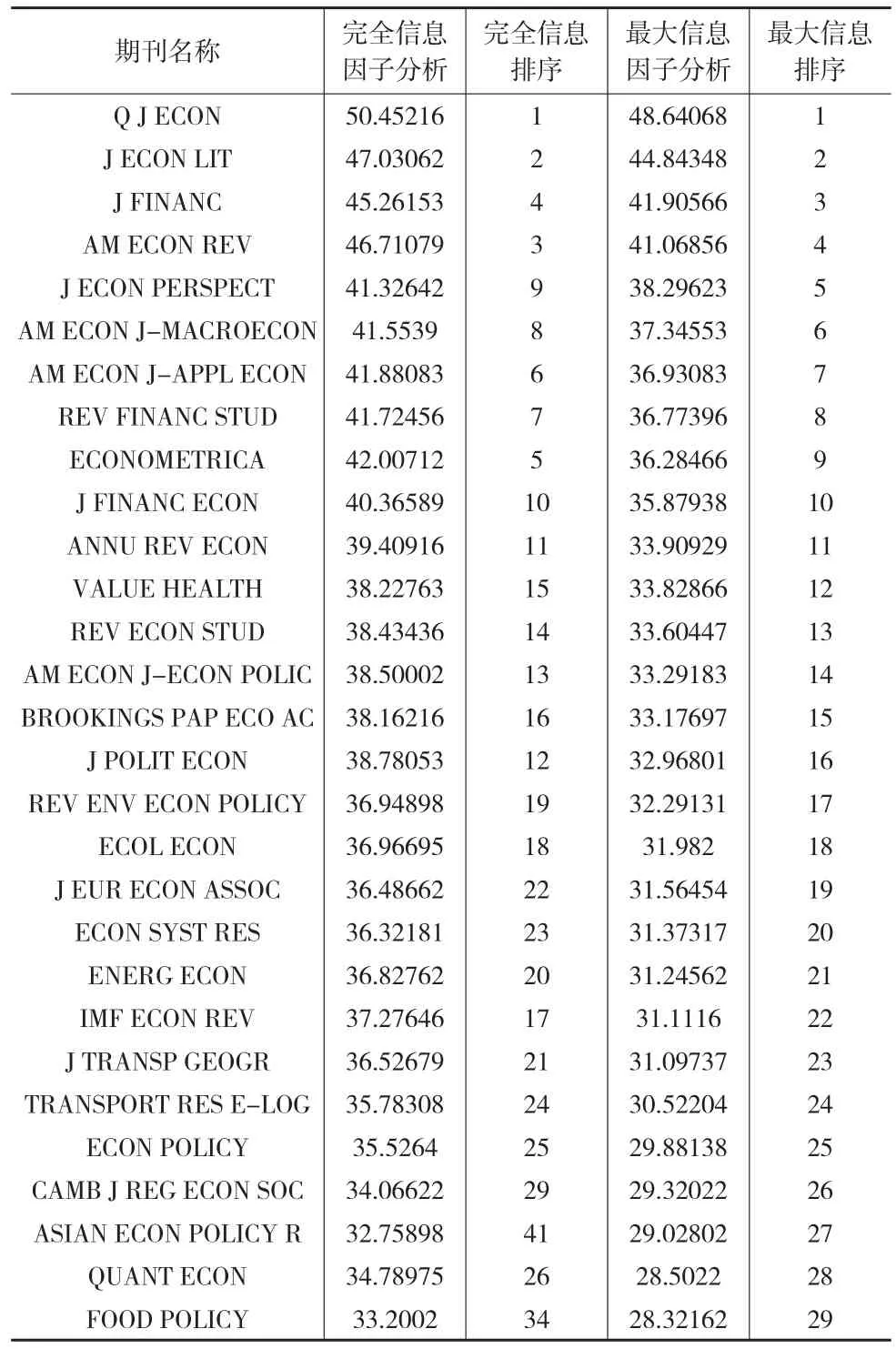
表6 完全信息因子分析與最大信息因子分析結果比較

同樣匯出完全信息因子分析評價結果與最大信息因子分析評價結果的散點圖（見圖3），兩者不僅相關度高，而且幾乎呈現一條直線，兩者的相關系數高達0.982，說明最大信息因子分析評價雖然也犧牲了原始數據的部分信息，但是與因子分析方法評價相比，已經得到很大提升，關鍵是通過其他方法賦予權重體現了評價為管理服務，具有較強的適用性。

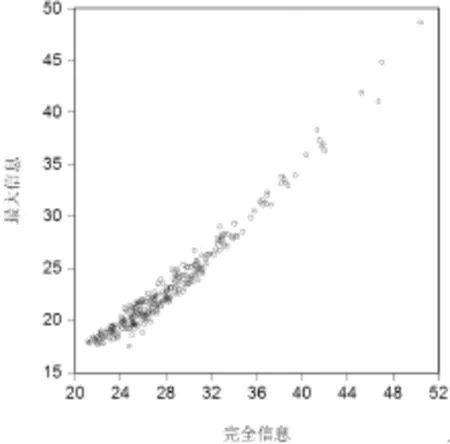
圖3完全信息因子分析與最大信息因子分析評價結果對比

3 結論與討論

（1）因子分析法評價會損失原始數據的大量信息

因子分析法評價由于采用少數公共因子進行加權匯總評價，這樣會丟失原始數據的大量信息，從而影響評價結果。本文分析發現，因子分析法通過降維增加了公共因子的解釋能力，從而便于進行深入分析，但是降維本身并沒有精簡計算，也沒有減少評價指標的數量從而降低評價成本，因此以犧牲原始數據信息為代價的因子分析評價并不具備太多的優勢。

（2）完全信息因子分析評價彌補了因子分析評價的信息不足

完全信息因子分析評價克服了傳統因子分析評價的弊端，完全不會犧牲原始數據信息，而且保留了因子分析方法的優點。本文研究發現，雖然傳統的因子分析評價結果與完全信息因子分析評價結果高度相關，但是對于評價對象個體而言，兩種評價方法結果排序相差較大，不利于科技評價的公平公正。

當然，完全信息因子分析完全采用方差貢獻率大小進行賦權是值得商榷的，這是所有客觀評價方法面臨的問題。

（3）最大信息因子分析評價方便主觀賦權

最大信息因子分析法在盡可能保持原始數據信息的情況下，比傳統因子分析提取了更多的公共因子，而且這些公共因子互不相關，這樣在此基礎上，可以根據評價目的與管理要求采用其他方法確定權重進行評價，克服了完全信息因子分析完全進行客觀賦權的不足。

但最大信息因子分析雖然也犧牲了部分原始數據的信息，但總體上這種影響較小，不像因子分析評價那樣犧牲的信息量較大。

（4）對于傳統因子分析應該重分析輕評價

因子分析方法的優點無可替代，比如降維技術、客觀的洞察力、公共因子不相關等，因此因子分析更適合對數據進行分析，但是從評價的角度，這并不是因子分析的強項，但可以借用。本文在因子分析的基礎上提出了完全信息因子分析與最大信息因子分析兩種評價方法，前者不會犧牲原始數據的任何信息但不宜主觀賦權，后者在盡可能少犧牲原始數據信息的情況下結合主觀賦權進行評價，各有特點，可以根據需要靈活選用。