基于ANSYSworkbench輪軸過盈裝配過程分析

孫林平，伍世云，楊麗萍，王 貴

（四川文理學院 智能制造學院，四川 達州635000）

1 引言

無鍵的過盈配合常常用于高速旋轉主軸中傳遞扭矩和軸向載荷，過盈配合屬于高度非線性問題，傳統依靠厚壁筒的理論公式進行計算，同時借助于有限元對其仿真.

有些研究利用ANSYS參數化對軸套過盈配合進行分析過盈量、彈性模量、內外徑、摩擦因數等對接觸壓力在軸向上分布的影響規律，并總結出代數關系式，方便進行計算.［1－3］有些研究利用有限元分析平臺分析輪軸接觸壓力和拔出力，通過參數綜合，總結出過盈力與設計參數之間的關系方程.［4－5］有些研究建立了高速旋轉主軸與轉子額過盈配合模型數值模擬過盈量、旋轉速度對過盈配合面間的應力、位移、接觸應力的影響.［6－8］

本文從ANSYS workbench平臺入手，對過盈配合的接觸狀態進行分析；并對其拆卸過程進行仿真研究，表明過盈配合是不適合拆卸后再使用.

2 過盈連接相關計算

主軸過盈配合設計主要從材料失效和防止結合面的滑動兩個部分考慮，根據外界需傳遞的扭矩、承受的軸向載荷等因素計算所需的最小接觸應力Pmin：

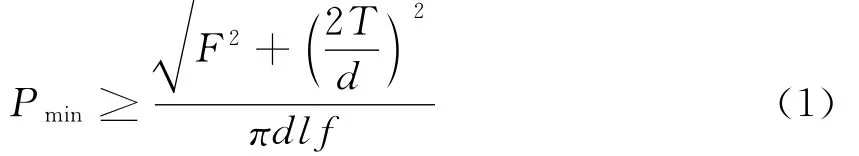
式中：F—軸向力，N；T—轉矩，N.m；d—公稱直徑，mm；l—配合長度，mm；f—摩擦系數.

則最小過盈量：

式中：Eα—包容件彈性模量；Ei—被包容件彈性模量；Cα，Ci—剛性系數νi—泊松比.

根據被連接件不產生塑性變形所應許最大結合面壓力Pmax：

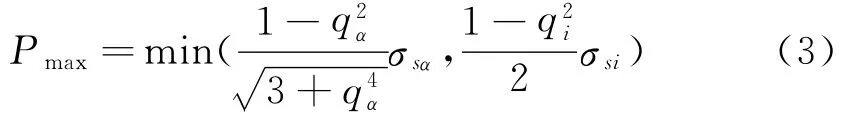
式中：σsα，σsi—材料屈服極限，MPa；

則最大過盈量：

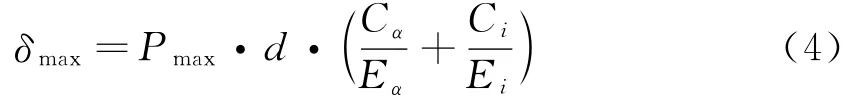
根據δmax，δmin選取公差配合.

3 仿真分析

3.1 模型的建立（過盈情況下的應力與拆卸應力）

由于軸對稱，采用1／4作為研究對象對其進行建模，如圖1所示，網格劃分采用掃描網格（圖2），共計約28000個節點.

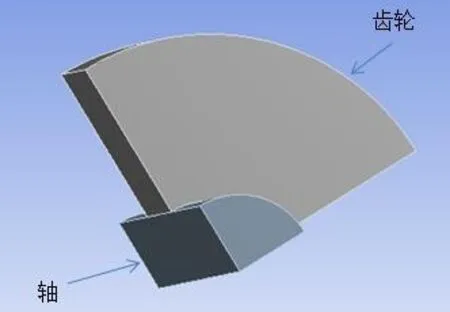
圖1 模型

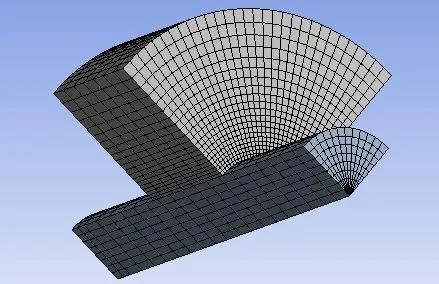
圖2 網格劃分

3.2 邊界條件

在其端面施加對稱約束，摩擦系數取0.2，過盈量設置為20um，本次分析共采用2個分析步，第一個分析步為靜態分析步（3s），第二個分析步為將齒輪外端面固定，給軸施加軸向位移50mm.

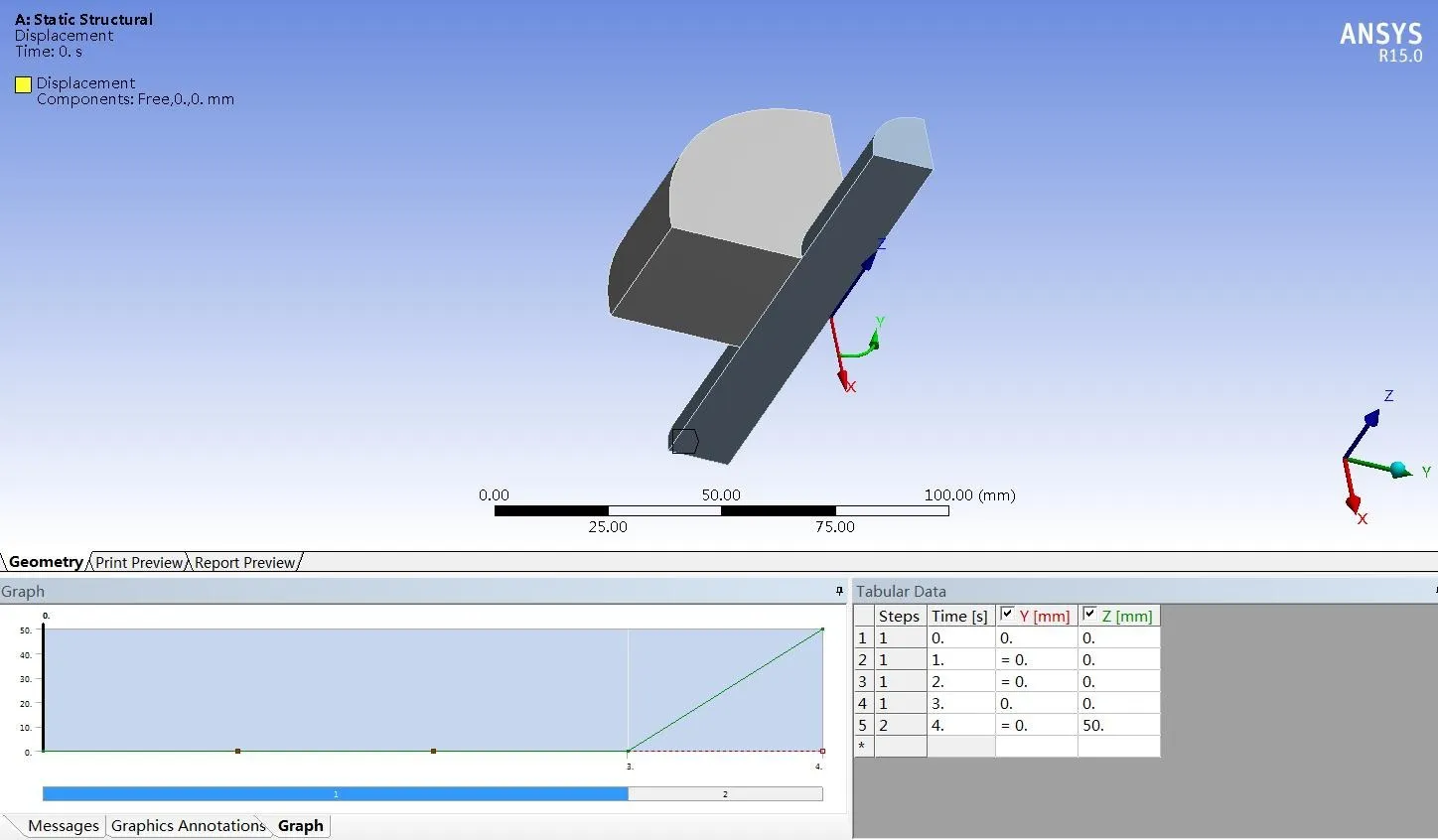
圖3 邊界條件設置

3.3 結果分析

（1）過盈情況下的應力、沿路徑應力分布

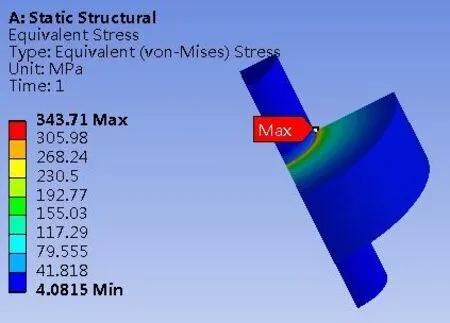
圖4 Mises應力云圖

圖5 接觸壓力分布

從圖4中可以看出在初始靜態情況下的最大應力出現在齒輪的內孔邊緣，最大為343.7MPa，故建議此處應倒圓角，減下應力.圖5中為靜態情況下接觸面的接觸壓力，其最大接觸壓力為188.4 MPa，也出現在齒輪的內孔邊緣.

沿路徑上應力分布情況：

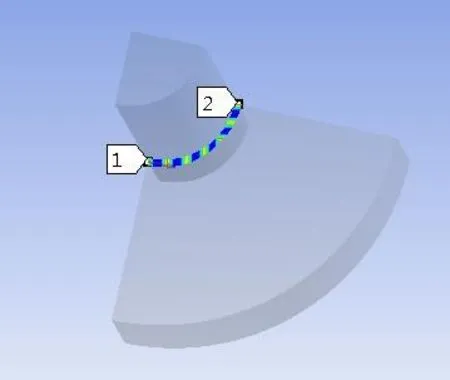
圖6 圓環路徑

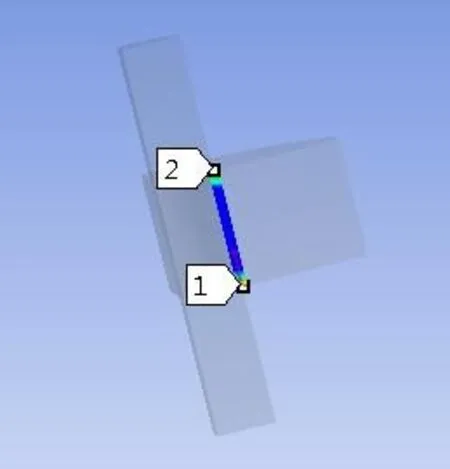
圖7 軸向路徑

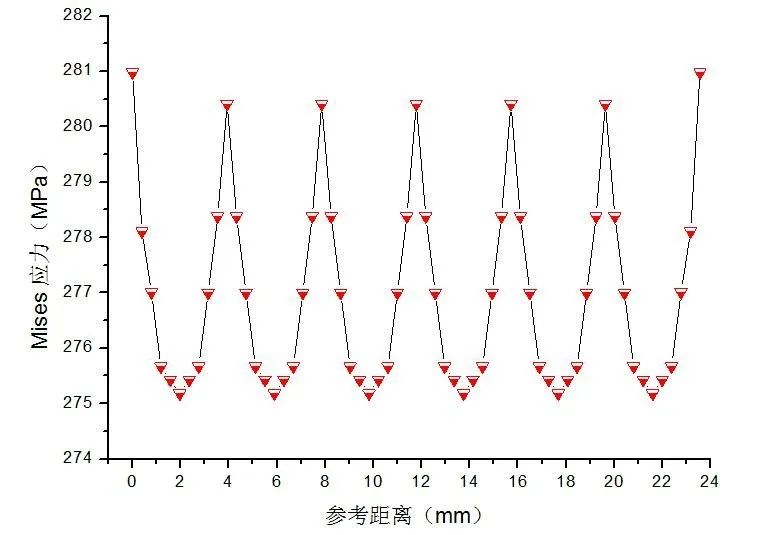
圖8 圓環路徑上的應力分布

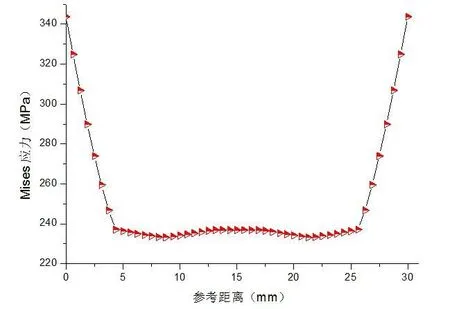
圖9 軸向路徑上的應力分布

圖6 的路徑為齒輪內孔的圓環，從圖8中可以得出：Mises應力在此路徑上呈整蕩起伏循環狀態，其值約在275MPa到281MPa之間，變化幅度不大；圖7的路徑為齒輪內孔軸向方向，圖8可以得出Mises應力沿此路徑呈U型分布，在兩端處應力比較集中約為340MPa，在中間位置應力分布較為均勻，約為238MPa.

（2）拆卸情況下的應力分布

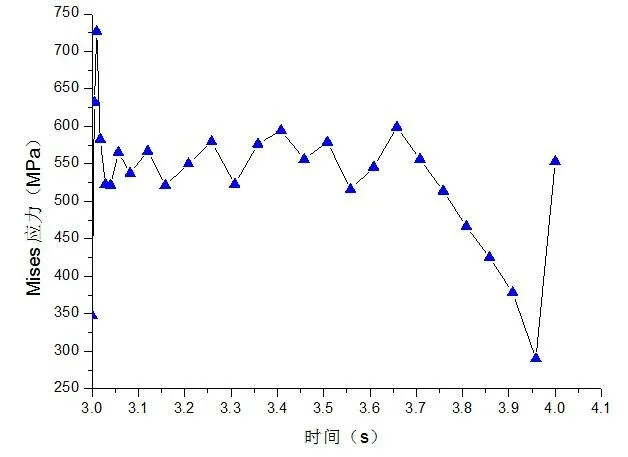
圖10 拆卸應力—時間歷程

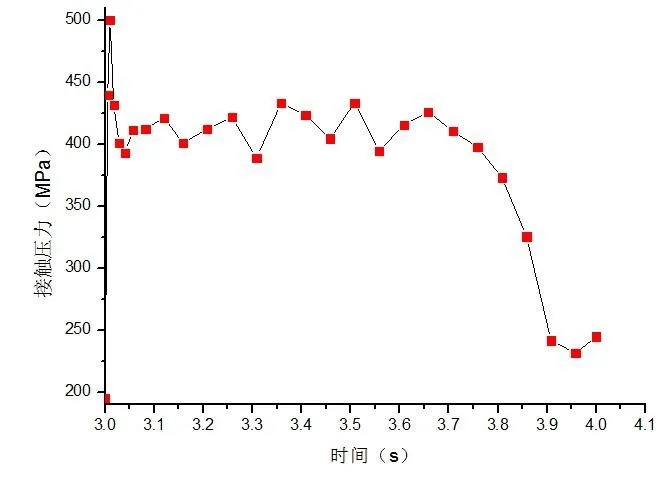
圖11 拆卸過程接觸壓力—時間歷程

圖12 拆卸過程中最大應力位置

圖13 拆卸過程中接觸壓力最大位置

從圖10可以看出拆卸過程中，Mises應力隨著時間的增加出現大幅度的波動，其最大值約為726.7MPa，其位置如圖12所示，已經遠遠超出了材料的許用應力［σ］＝460MPa，所以過盈裝配作為一種典型的不可拆卸原理.圖11為接觸面上的接觸壓力時間歷程，可以得出在拆卸的起始點接觸壓力較大約為499MPa，如圖13所示，整個過程壓力值波動后下降，但其最大接觸壓力也超出了材料的許用應力，在此證明過盈裝配不適合拆卸后再使用.

結 論

（1）利用 ANSYS workbench平臺對過盈裝配的接觸狀態進行分析，配合面的最大Mises應力和接觸壓力都出現在內孔邊緣，但處于安全范圍之內；配合面的最大Mises應力沿圓環路徑呈整蕩起伏循環狀態，但波動不大；沿軸向路徑呈U型分布，兩端應力值較大.

（2）分析過盈裝配在拆卸的情況下，最大Mises應力、接觸壓力都出現了大幅度的波動，最大值都超過了材料的許用極限，表明過盈裝配不適合拆卸后再使用.