基于控制系統工作原理的視線角速度獲取方法

劉浩偉，張衛華，王 興，伍玲玲，吳丹麗

(1. 中國航天科技集團有限公司 紅外探測技術研發中心，上海 201109； 2. 上海航天控制技術研究所，上海 201109)

0 引言

本文基于角跟蹤原理推導了視線角速度方程，建立了3種視線角速度獲取模型，利用卡爾曼濾波方法對3種模型進行了仿真計算，并對其有效性進行了對比分析。

1 導引頭角跟蹤原理

1.1 坐標系定義及符號約定

圖1為典型紅外導引頭目標跟蹤示意圖。定義彈體坐標系OM-XMYMZM：坐標原點OM為彈體質心；OMXM軸為彈體縱軸，指向目標為正；OMZM為彈體俯仰軸；OMYM為彈體偏航軸；三軸方向符合右手定則。彈體坐標系繞彈體俯仰軸和偏航軸旋轉得到導引頭光軸坐標系OP-XPYPZP。定義視線坐標系OS-XSYSZS：原點OS取在平臺旋轉中心處；OSXS為彈目視線方向，指向目標為正。

圖1 紅外導引頭目標跟蹤示意圖Fig.1 Schematic diagram of infrared seeker target tracking

1.2 導引頭角跟蹤原理

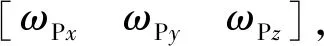
(1)

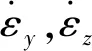
因探測器輸出失調角[εyεz]都是小角度，故可做小角度近似sinεy≈εy，cosεy≈1，且將多于2個正弦項的乘積近似為0，得到角跟蹤簡化方程為

(2)

2 視線角速度獲取數學模型

2.1 直接微分法模型

2.2 基于馬爾科夫模型的視線角速度獲取模型

假設目標做機動運動，則目標的隨機加速機動可被視為修正的瑞利-馬爾科夫過程。此處，目標加速度采用零均值一階時間相關模型。考慮方位與俯仰方向的交叉耦合，可將目標機動模型表示為

(3)

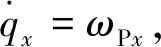
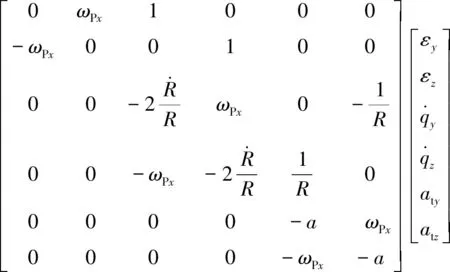
(4)

式中：asx，asy，asz為彈體運動加速度。

角跟蹤系統的量測值為視線角速度εy,εz，量測方程為

(5)

式中：ny，nz為探測器量測噪聲，可近似為白噪聲。

2.3 基于控制系統工作原理的彈目視線角速度獲取模型

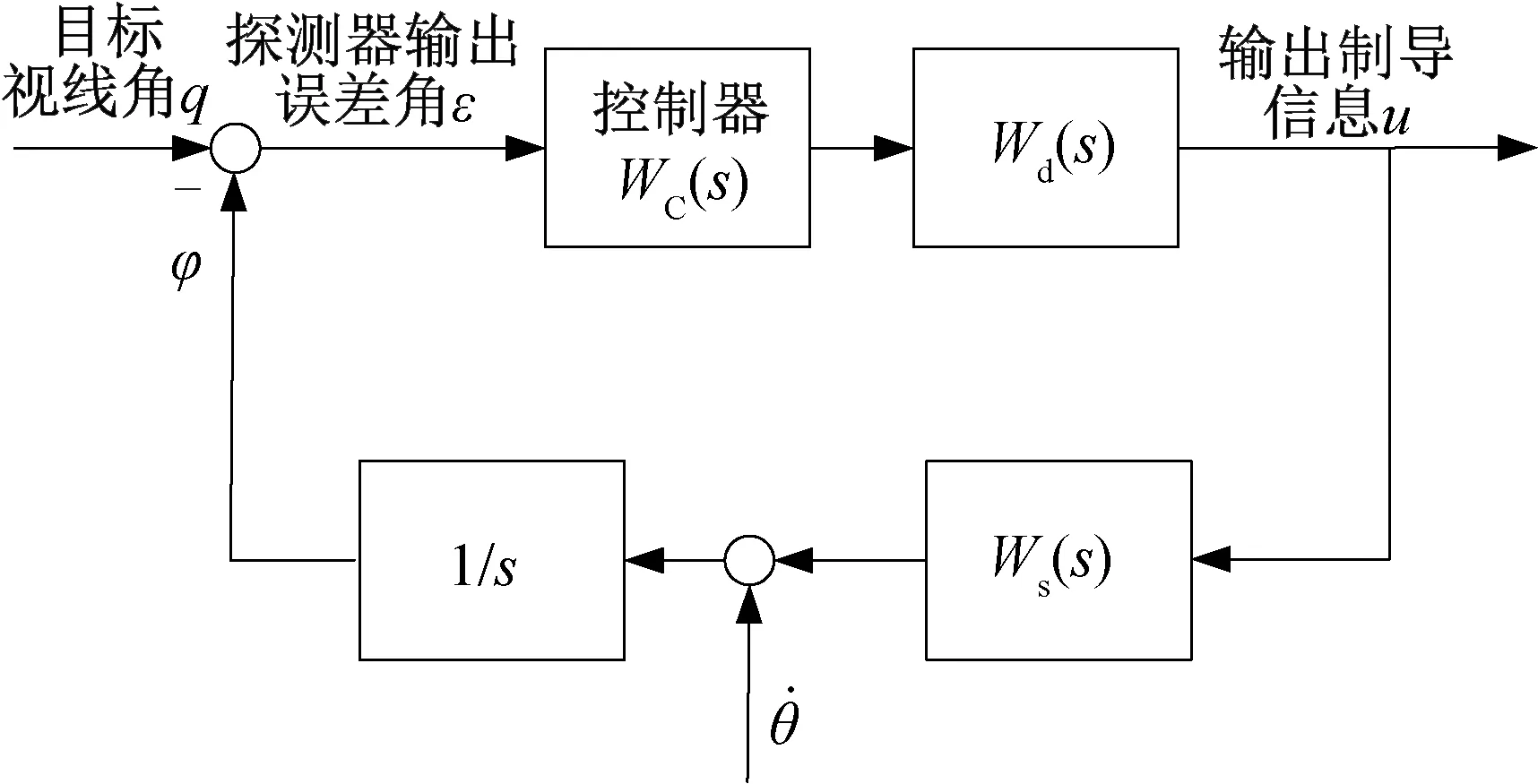
圖2 紅外跟蹤回路簡化結構圖Fig.2 Simplified structure diagram of infrared seeker angle track loop

推導輸出制導信息過程為

(6)

得到導引頭輸出制導信息為

(7)

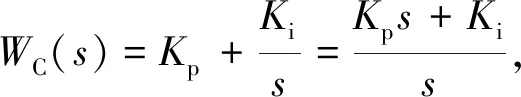
推導在此模型下探測器誤差角ε與目標視線角q的關系為

(8)

(9)

(10)

忽略q(t)的三階以上導數較小，認為是誤差項，可得

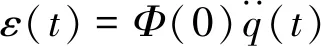
(11)

由式(10)可知，當設計的控制器滿足Φ(0)很小時，探測器輸出的失調角ε(t)可以很小，推導彈目視線角加速度公式為

(12)

將上式與角跟蹤方程聯立，建立狀態方程與量測方程為

(13)

(14)

3 仿真結果與分析

3.1 卡爾曼濾波算法

作為一種線性遞推最小方差估計方法，卡爾曼濾波算法以其廣泛的適用性在多個工程領域發揮重大作用。卡爾曼濾波算法是獲得系統狀態最優估計的有效方法，能根據不同測量量估計出無法直接測量的變量。在陀螺的輸出信號中引入卡爾曼濾波，從概率統計最優的角度估算出陀螺角速度誤差并進行補償，可實現高精度跟蹤和穩定[8-9]。

系統的狀態方程和量測方程為

(15)

式中：Xk為狀態變量；Wk為系統噪聲；Vk+1為量測噪聲；φk+1,k為系統狀態轉移矩陣；Γk+1,k為噪聲輸入矩陣；Hk+1,k為觀測矩陣。

得到自適應卡爾曼濾波算法為

(16)

式中：Pk+1,k為一步預測誤差方差陣；Rk+1，Qk為系統噪聲方差陣，Rk+1=E[Vk+1(Vk+1)T]，Qk=E[Wk+1(Wk+1)T]；Gk+1為濾波增益矩陣；Pk為估計誤差方差陣。

3.2 仿真結果與分析

目標靜止不動，彈體以3(°)/Hz的角速度擺動時的測試結果如圖3所示。

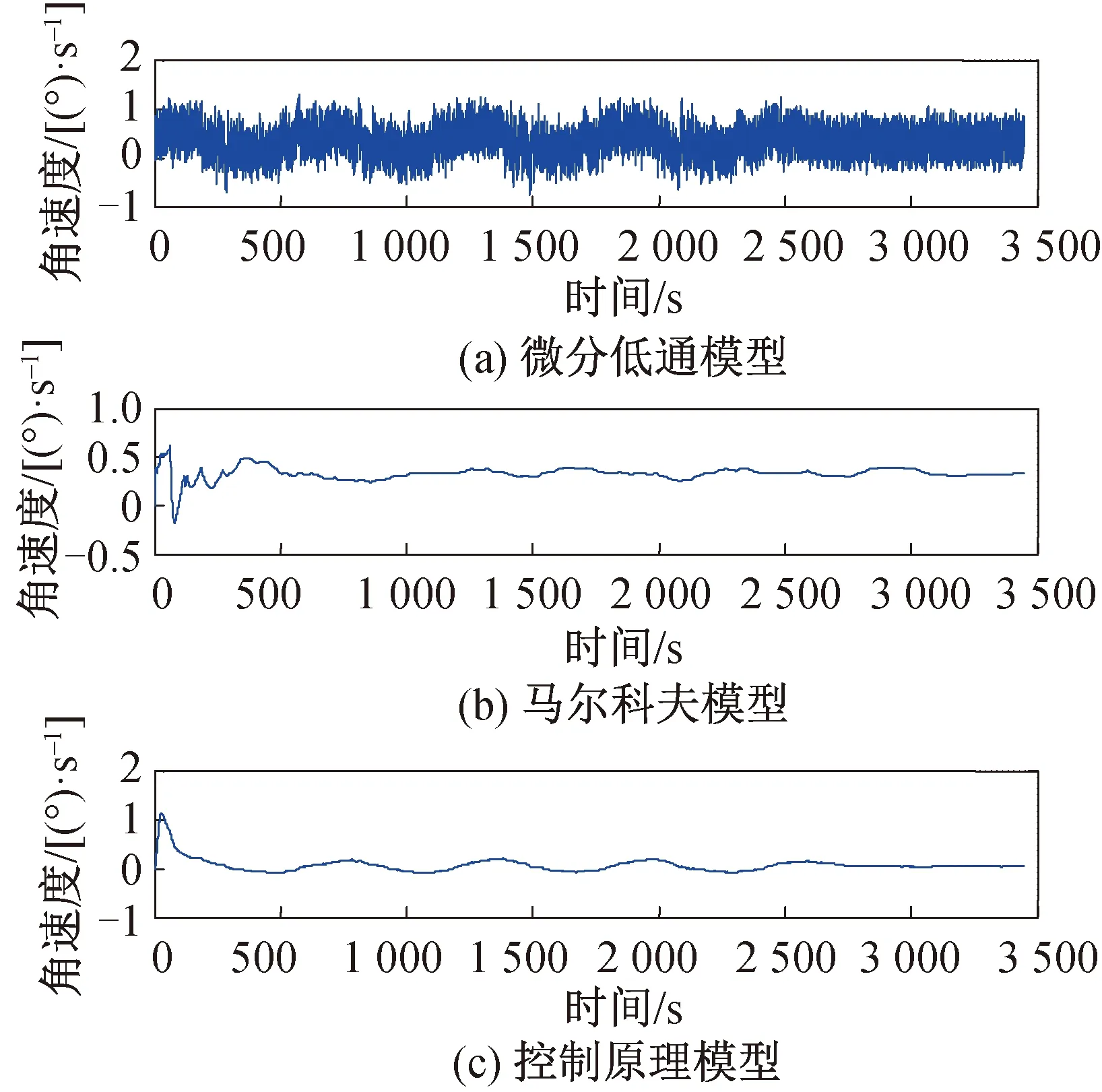
圖3 目標靜止時彈目視線角速度Fig.3 Line-of-sight angle rate for stationary target

目標往返運動時的測試結果如圖4所示。

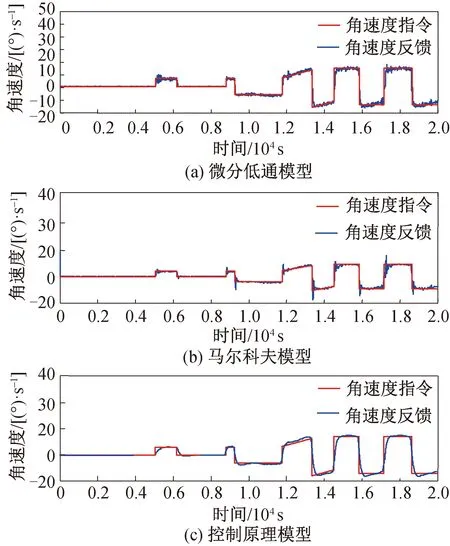
圖4 目標往返運動時彈目視線角速度Fig.4 Line-of-sight angle rate for maneuvering target

分析圖3，4曲線可以發現：微分法帶來的角速度噪聲太大，盡管加上低通濾波，可適當降低噪聲，但難以消除彈體擾動影響，實際應用受限；基于馬爾科夫模型的彈目視線角速度提取算法需要彈目距離信息和彈目接近速度信息，且受限于建立的馬爾科夫模型的準確度，實際應用受限；基于控制原理的彈目視線角速度提取算法實現簡單方便，不需要距離信息，僅需要利用陀螺和探測器失調角，過渡過程平穩，快速性滿足使用要求，角速度穩定精度達到0.05(°)/s以內，滿足彈體制導指標要求。

4 結束語

本文對紅外導引頭視線角速度提取方法進行了研究，比較分析了直接微分法、基于馬爾科夫模型的方法和基于控制系統工作原理的方法3種彈目視線角速度提取方案。微分法需要對陀螺輸出和探測器失調角微分輸出進行傳遞函數匹配，并進行濾波，難度較大，工程實現復雜；基于馬爾科夫模型的彈目視線角速度提取模型需要獲得彈目距離信息和彈目接近速度信息，但因紅外導引頭無法獲得這些信息，故該模型在紅外導引頭中的應用受到限制。本文提出將角跟蹤系統設計成二階無靜差系統，將由控制系統工作原理推導的失調角與彈目視線角加速度成正比這一結論和由角跟蹤原理獲得的彈目視線角速度提取基本模型進行結合，提出了基于控制系統工作原理的彈目視線角速度提取方法。基于控制系統工作原理的彈目視線角速度獲取方法在導引頭中屬于首次應用。該方法不依賴彈目距離信息，只需要陀螺、探測器坐標信息和控制系統模型信息，具有實現簡單、運算量小、精度高的特點。實驗室仿真驗證彈目視線角速度精度由原來的1(°)/s提高到0.05(°)/s以內，滿足使用要求。但是該方法在實際工程應用時，要對陀螺輸出信息進行建模，且要盡可能準確獲取控制系統模型參數，因此需要進一步研究陀螺噪聲建模方法和控制系統辨識方法。