基于脈沖初值的小推力轉移軌道優化研究
王旭生,施偉璜,王 偉,彭玉明
(1.上海衛星工程研究所,上海 201109; 2.上海市深空探測技術重點實驗室,上海 201109)
0 引言
深空探測是當今世界航天活動的熱點研究領域,是一個國家綜合國力和創新能力的體現。我國已將深空探測納入國家重大科技專項,正在實施首次自主火星探測任務,并規劃了多目標小行星探測、火星取樣返回、木星系及行星穿越等任務。其中,小行星探測任務的總速度增量要求大于8 km/s,由于傳統低比沖的化學推進系統無法使用,因此小推力、高比沖、高可靠的電推進系統成為工程實施的優選動力形式。
在小推力作用下,深空探測器的軌道優化在本質上是一個最優控制問題。目前求解方法主要有直接法、間接法和混合法[1],它們都不可避免地需要進行初值猜測。初值猜測不僅在理論上作為算法的啟動值必不可少,而且在工程應用上也是粗略優化的過程,可提供任務可行性、性能指標、各階段大致時間節點等關鍵信息,為進一步優化軌道提供參考。脈沖軌道作為小推力轉移軌道的初值,具有形式簡單、計算方便的優點,被廣泛應用于小推力轉移軌道優化的求解,如:美國噴氣推進實驗室(JPL)基于圓錐曲線拼接法開發了MALTO軟件包的初值,采用一系列脈沖替代小推力軌道[2],該方法已應用于木星冰衛星軌道器任務的軌道設計中[3];陳揚等[4]基于脈沖估算結果設計了電推進軌道,采用間接法求解燃料最優控制問題,得到了小推力的最優軌跡;李九天[5]提出了基于小推力可實現性的脈沖軌道約束,研究了基于該約束的燃料最優脈沖轉移軌道設計方法;蔣小勇等[6]提出了一種基于多沖量能耗估算的任務窗口搜索方法,可用于搜索小推力任務的發射窗口。以上研究均基于單一形式的脈沖初值,在工程應用中未考慮脈沖軌道的多樣性,缺少對不同形式的脈沖初值與小推力優化結果之間影響關系的分析。
本文基于小行星探測任務,以燃料最優為性能指標,提出了一種采取粒子群優化(PSO)和序列二次規劃(SQP)的組合優化算法,可適應于不同形式的脈沖初值輸入,并保證收斂性;設計了地球1∶1共振近地小行星2016HO3交會任務的小推力轉移軌道,給出了軌道設計參數;對比分析了可用于小推力轉移軌道優化初值結果的3種典型脈沖軌道,討論了不同脈沖初值對小推力轉移軌道優化結果的影響。
1 小推力轉移軌道優化問題
在日心黃道慣性坐標系下,探測器典型的二體動力學方程為
(1)
式中:r,v為探測器的位置矢量和速度矢量;U為發動機的推力矢量,U=[FxFyFz];m為探測器的瞬時質量;Isp為發動機比沖;f為除發動機推力加速度之外的攝動加速度;g0為海平面重力加速度。r,v,m為狀態變量,X=[rvm]。將式(1)簡寫為
(2)
將小推力軌道優化問題轉換為尋找最優控制函數U(t),并使性能指標
J=J(tf,Xf)
(3)
達到最小,同時滿足動力學方程約束條件、初末狀態約束條件、路徑約束條件,即
(4)
X(t0)=X0,X(tf)=Xf
(5)
ψ(U(t))≤0
(6)
2 優化數學模型
小推力軌道優化問題的最優控制描述形式會引入無明顯物理意義的協態變量,導致收斂域窄,造成初值猜測困難[7]。本文基于直接法的離散思想,建立非線性規劃(NLP)形式的小推力轉移軌道優化數學模型。以離散節點的中點作為強制匹配點,將微分方程約束轉化為殘差形式的等式約束。
將整個飛行時間分為N個時間段,各節點處的時刻為
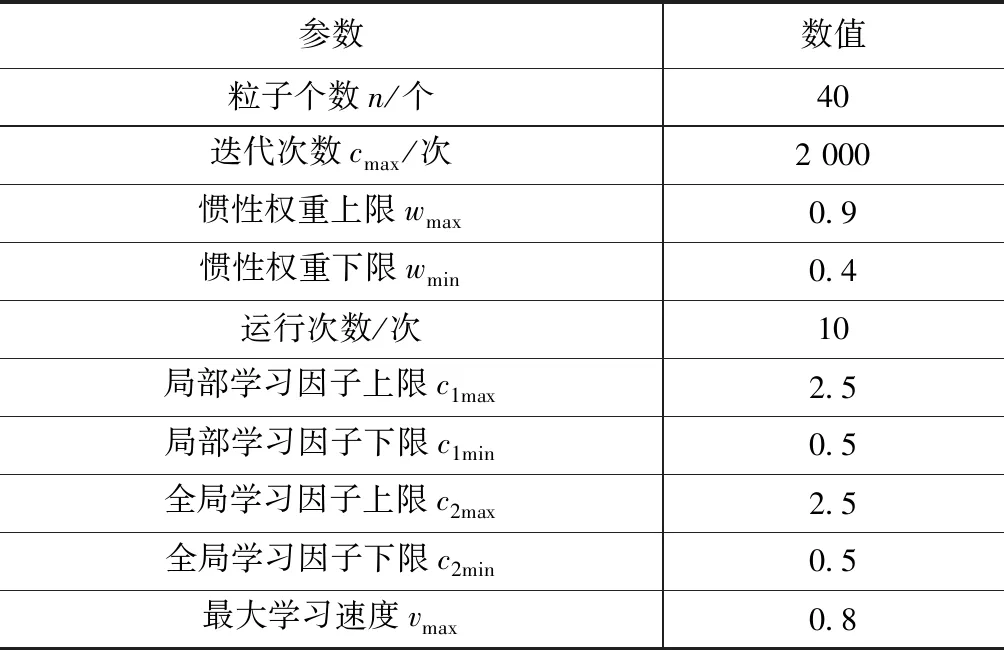
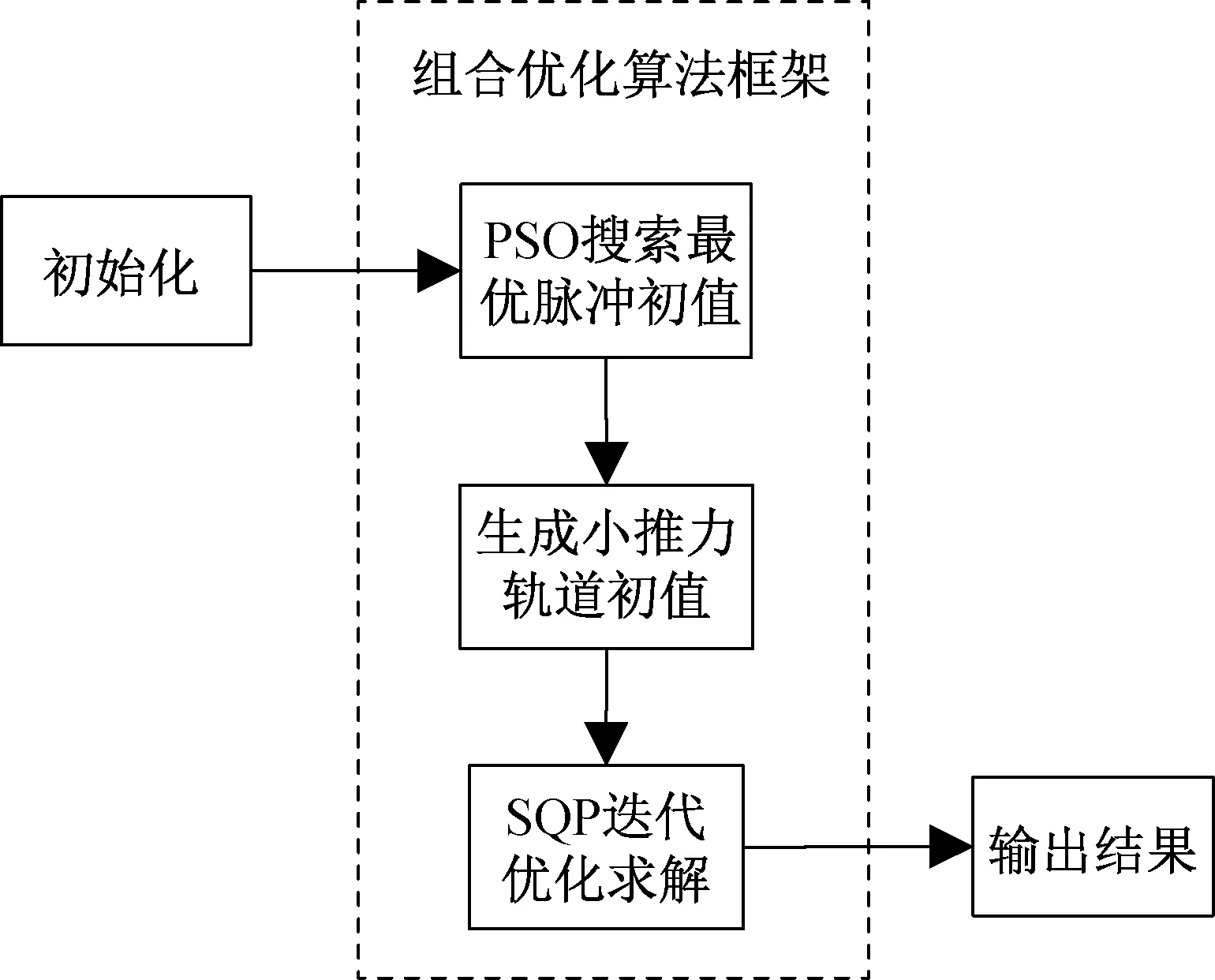
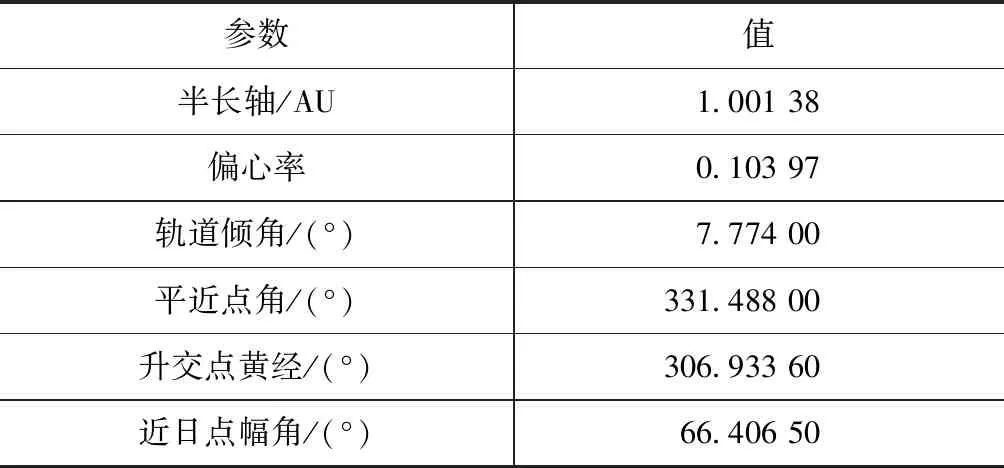
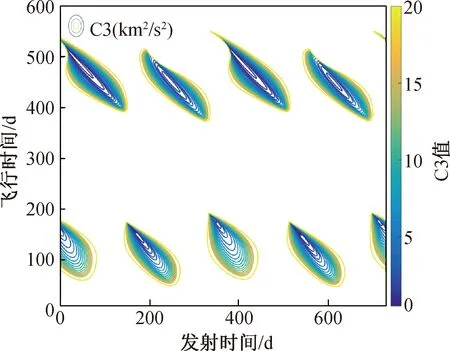
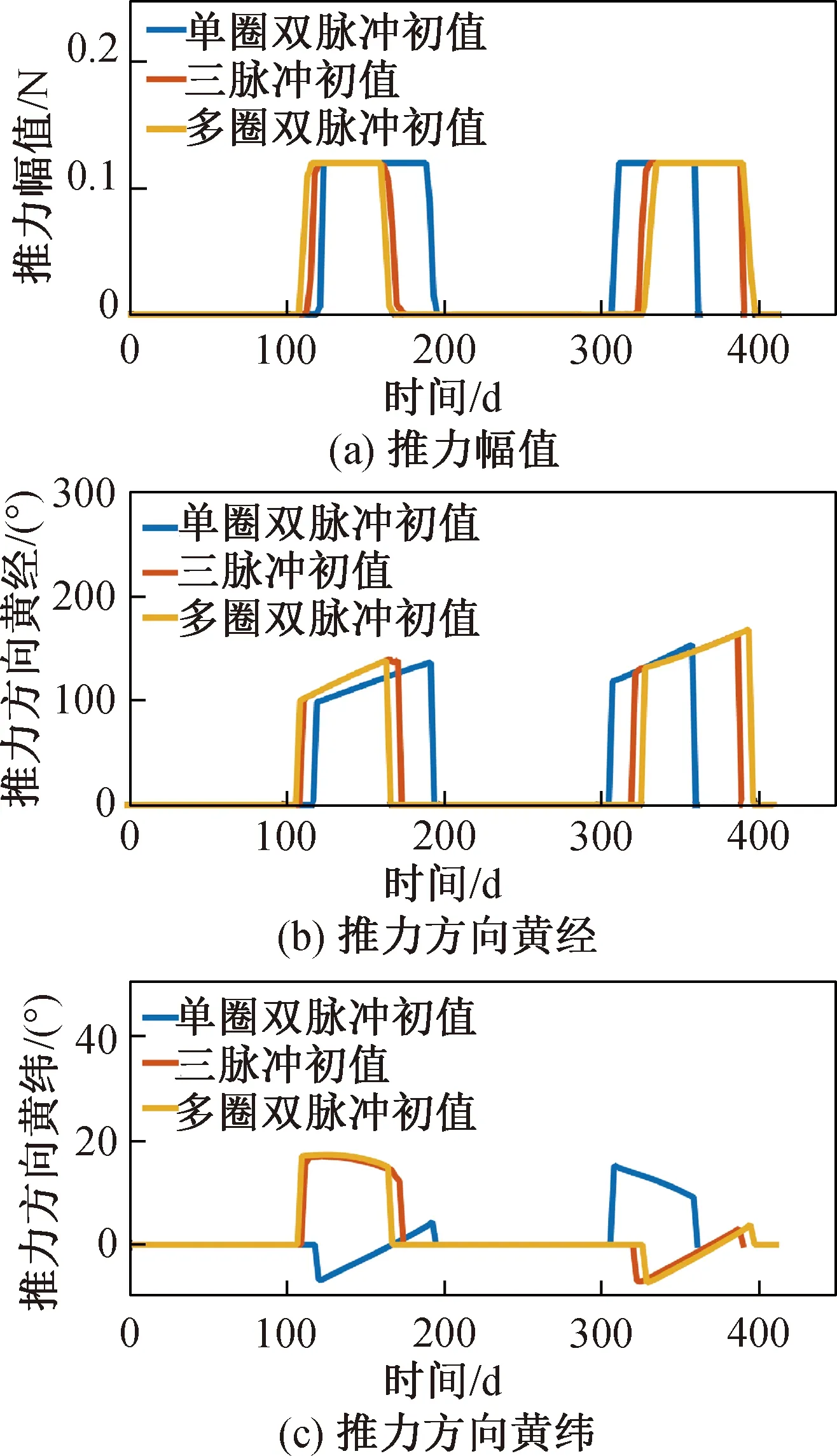
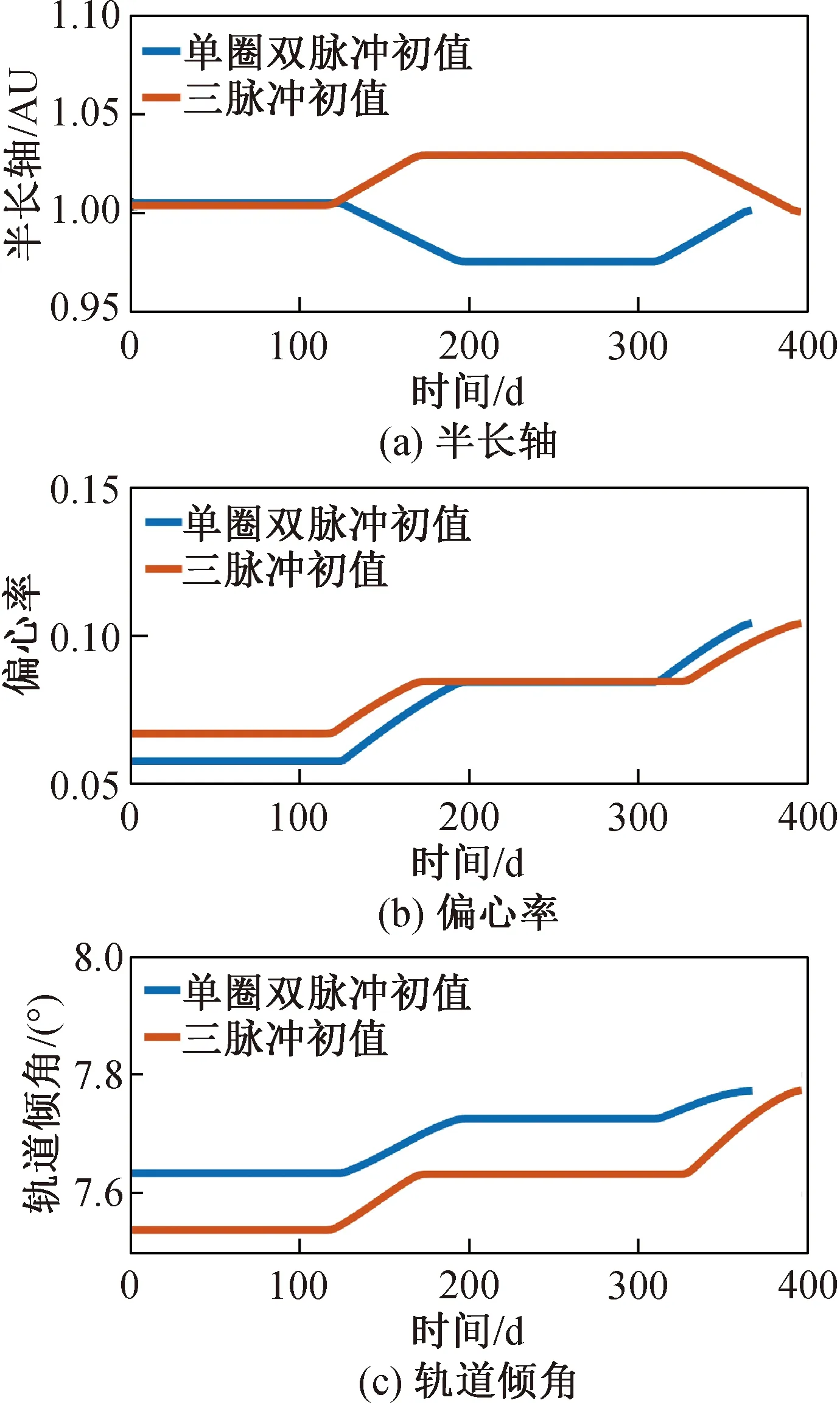
t0 (7) (8) 則S∈[0,1]。對狀態變量進行三階Hermite插值,控制變量采用線性插值。以x代表狀態變量的任一分量,則 x=C0+C1S+C2S2+C3S3 (9) (10) (11) (12) 對于狀態變量中任一分量均可執行上述操作。至此,連續的動力學方程約束轉化為離散的7N個等式約束。 在離散形式下,初始狀態與終端狀態分別與出發天體和到達天體的位置速度相同,即 (13) 給定出發時間和到達時間,通過查找星歷獲取出發、到達天體的位置速度。末端質量自由,初始質量為發射質量,假設發射質量為m0,則 m(t0)=m0 (14) 離散形式的路徑約束為各節點處的推力值小于等于最大推力值Fmax,即 ‖U(ti)‖≤Fmax (15) 以燃料最優為指標,將離散形式表示為 (16) 至此,小推力轉移軌道問題優化的數學模型完成建立。尋優變量Z={t0,tf,X0,…,XN,U0,…,UN},優化指標為式(16),約束條件為式(12)~(15)。其中,約束條件和性能指標可根據具體情況進行相應修改。 傳統PSO算法具有全局優化和并行計算的能力,相比于經典的基于梯度的優化算法具有更好的全局收斂性[9],但PSO算法出現早熟現象的概率較大,以致收斂于局部最優解。為此,本文通過線性減小慣性權重系數和局部學習因子,增大全局學習因子,使算法在初期具備較強探索能力,在后期又有較好的收斂性,使其在最優解附近精細搜索。本文算法主要包括以下步驟。 1) 初始化粒子群位置p和速度v,粒子位置信息包含脈沖作用時刻和脈沖作用矢量。 2) 對每個粒子用構造的位置函數Fitness進行評價,此時Fitness為總速度增量。 3) 更新每個粒子的歷史最優位置pb和群體的全局最優位置gb。 4) 分別按照式(17),(18)更新每個粒子的速度和位置,其表達式為 vi+1=w·vi+c1·rand()·(pb-p)+ c2·rand()·(gb-pb) (17) pi+1=pi+vi+1 (18) 式中:w為粒子的慣性權重系數;c1為局部學習因子;c2為全局學習因子;rand()表示0~1的隨機數。同時設置粒子學習速度在[-vmax,vmax]內,若更新后的速度超出邊界,則取相應的邊界值。w,c1,c2的更新依據為 (19) (20) (21) 式中:c為運行代數;cmax為最大運行代數。 5) 判斷終止循環條件。若條件不滿足,則循環執行步驟2~4;若滿足,則輸出結果,生成初值Z0={t0,tf,X0,…,XN,U0,…,UN}0。其中,{t0,tf}和{X0,X1,…,XN}中的位置和速度分量可直接從結果中生成,質量可基于其消耗特性按等差遞減生成;{U0,U1,…,UN}0可在[0,Fmax]內隨機猜測。為避免隨機性對結果帶來的影響,Ui0=Fmax[0.5, 0.5, 0.5]。算法相關參數設置見表1。 表1 粒子群算法參數 SQP算法是求解NLP問題的有效算法[10],但SQP算法是基于可行方向搜索的一種約束優化方法,其只具有局部優化能力,因此將SQP與PSO算法結合可充分發揮兩者優勢。算法的主要步驟如下。 1) 給定PSO算法搜索后生成的初值Z0,選定正定矩陣H0。 2) 求解的二次規劃問題為 mindT s.t. con(Zk)+dTcon(Ζk)≤0 (22) 式中:obj為目標函數;con為約束;dk為搜索方向,當‖dk‖<10-6時,迭代結束。 3) 更新Zk+1=Zk+αkdk,其中αk由線性搜索確定。 4) 修正Hk,使Hk+1保持正定。 5) 判斷是否滿足迭代終止條件:若迭代次數超過2 000次或‖dk‖<10-6,則迭代結束;否則重復步驟2~4。 為便于計算,初值生成過程和優化求解過程的尋優變量均進行歸一化處理。組合優化算法的流程如圖1所示。 圖1 組合優化算法流程Fig.1 Combinatorial optimization algorithm flow 2016HO3是2016年發現的1顆阿波羅型地球1∶1共振近地小行星,其日心軌道周期與地球公轉周期呈現1∶1的關系。雖然2016HO3為繞日小行星,但是其相對地球的軌道較穩定,因此被稱為地球的第2個月亮。該小行星具有獨特的探測價值,是我國小行星探測任務的首要備選目標,其軌道參數見表2。表中:AU為天文單位;MJD為約化儒略日。 分析不同初值對優化結果的影響。假設探測器的發射質量為1 500 kg,發射日期在2022年1月1日至2024年1月1日之間,飛行時間小于700 d。發射C3(離開地球引力影響球時與地球相對速度的平方)不大于20 km2/s2,2016HO3交會任務的發射C3等高線如圖2所示,發射時間從2022年1月1日開始。由圖可見:若僅從發射C3的角度考慮,則每年有4個發射窗口,平均每季度出現1次波谷,分為長轉移和短轉移,兩者交替出現。其中,長轉移時間約為380~550 d,短轉移時間約為50~200 d。 表2 2016HO3小行星軌道參數(MJD=58 000.0) 圖2 發射C3等高線Fig.2 Contour line of launch C3 假設小推力大小為120 mN,發動機比沖為3 500 s,推力大小和方向可調。選取單圈雙脈沖、三脈沖、多圈雙脈沖3種典型的脈沖初值軌道。將轉移軌道等時間間隔離散為150個軌道段,經PSO算法搜索后的初值軌道參數及經SQP算法優化后的小推力軌道參數見表3,由表可得: 1) 3種初值軌道優化后得到了2022年11月29日和2022年5月28日這2個發射窗口,其中三脈沖初值和多圈雙脈沖的初值總速度增量差距最大,但優化結果最為接近。 2) 優化軌道和初值軌道的發射時間與飛行時間具有強耦合關系,提供的初值飛行時間越長,優化得到的結果飛行時間也越長。SQP算法只是局部優化,因此優化軌道與初值軌道的飛行時間非常接近。 表3 2016HO3小行星交會任務軌道優化結果 3) 3種形式的脈沖轉移軌道總速度增量差距最大達58%,而3種小推力轉移方案燃料消耗差距不超過6%。由此可見,本文算法對初值的敏感度小,具有一定的全局優化能力。 各初值對應的小推力轉移軌道的控制曲線如圖3所示。圖中,推力方向以黃經、黃緯表示。 圖3 不同初值的最優控制Fig.3 Optimal control curves of different initial values 由圖3可見: 1) 小推力發動機基本符合滿推或關機的形式,即為Bang-Bang控制的小推力軌道最優控制形式[11]。 2) 最優小推力轉移軌道總體上存在2個主推進段,不同的脈沖軌道初值對應的最優控制曲線的差異主要體現在推力器開關機時刻的不同上。 3) 對于不同初值對應的優化結果,其推力方向的變化在相位上有明顯差別,可看出2個發射窗口對應2種推力變化形式。 4) 從飛行時間來看,多圈雙脈沖初值優化得到的小推力轉移方案在第2個推進段關機后有約10 d的自由飛行段。由此可見,三脈沖初值具有更優的性能。 圖4 燃料最優小推力轉移軌道根數變化Fig.4 Time histories of fuel-optimal low-thrust transfer orbital elements 單圈雙脈沖初值和三脈沖初值對應的小推力轉移軌道根數變化過程如圖4所示。由圖可見:對應于日期為2022年11月29日的發射窗口,發動機的工作序列為“先長后短”;對應于日期為2022年5月28日的發射窗口,發動機的工作序列為“先短后長”。11月的發射窗口與5月的發射窗口相比,當探測器從地球出發時,前者為小偏心率大軌道傾角,后者為大偏心率小軌道傾角。從半長軸變化趨勢來看,前者為先減小后增大,后者為先增大后減小。 為解決小推力軌道優化未考慮脈沖初值多樣性的問題,利用不同形式的脈沖軌道初值對小推力轉移軌道優化結果的影響進行了研究,提出了能適應不同脈沖初值的組合優化算法,以我國深空探測規劃背景任務中的小行星探測任務為例進行了仿真分析。針對近地小行星2016HO3交會任務,以3種典型的脈沖軌道優化得到了3種具體的小推力轉移軌道方案和2個發射窗口。其中,三脈沖軌道初值與多圈雙脈沖軌道初值對應的優化結果主要體現在開關機時刻的不同,單圈雙脈沖初值與三脈沖初值、多圈雙脈沖初值的優化結果主要體現在推力方向變化的差異,3種初值軌道對應最優小推力軌道燃料消耗量差距不超過6%。研究結果表明:本文算法對初值的敏感度低,能收斂于Bang-Bang最優控制形式;不同初值對小推力軌道的整體性能指標影響較小,但開關機時刻和推力方向的變化會產生較大差異,從而得到不同的最優控制曲線。該研究成果對小推力軌道優化初值的選取、我國未來小行星探測任務的工程實施具有一定的參考價值。由于本文未對2個窗口的控制策略進行優劣性分析,且優化模型僅以燃料消耗作為評價指標,未考慮軌道設計中飛行時間、控制誤差、多體模型等其他重要參考因素,因此后續將綜合考慮多種評價指標,進一步優化設計。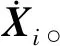
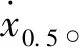
3 基于PSO和SQP的組合優化算法
3.1 PSO算法搜索脈沖初值
3.2 SQP算法求解NLP問題
4 近地小行星2016HO3交會任務

5 結束語

