航天器相對運動建模及周期性相對運動求解

劉柔妮，陳 杰，孔祥龍，周世宏

(1.上海衛星工程研究所，上海 201109； 2.上海航天技術研究院，上海 201109)

0 引言

航天器相對運動建模是編隊飛行等航天領域的研究熱點，研究空間自然條件下周期性相對繞飛軌道對長期編隊飛行航天器有十分重要的意義。通過找到不消耗能量的自然繞飛軌道，可節省編隊航天器系統的能量損耗，延長系統壽命。文獻[1]利用Hill方程和Clohessy-Willshire方程(簡稱HCW方程)進行編隊衛星構型設計，在圓參考軌道、無攝動和線性化的假設條件下，找到了周期性相對運動軌道存在的初始條件。LAWDEN[2]研究了橢圓參考軌道的相對運動。TCHAUNER等[3]以真近點角為獨立變量，通過限制參考基準軌道偏心率避免了Lawden方程存在的奇點問題。TILLERSON等[4]研究了橢圓軌道中編隊飛行衛星的控制問題。ALFRIEND等[5]率先采用相對軌道要素描述相對運動。肖業倫等[6]也采用相對軌道要素描述相對運動。之后，韓潮等[7-8]在該概念的基礎上進行了一定的研究工作。但以上研究成果均存在不足：Hill方程和Clohessy-Willshire方程使用條件苛刻，需要圓參考軌道、線性化的假設前提，工程應用受到限制；真近點角、相對軌道要素等描述方式較難考慮周期性相對運動的初始條件，求解難度較大。

本文采用哈密爾頓-雅可比(HJ)方程和正則攝動理論，引入適當的正則變量描述相對軌道運動，建立適用于橢圓參考軌道，便于考慮各種攝動的相對運動模型。經推導發現，在各種攝動下相對運動的哈密爾頓方程可分解為線性項和攝動項，而相對運動在任意攝動情況下的解可通過求解包含正則變量的微分方程和修正線性項得到，且模型滿足攝動疊加原理，即如已得到一定攝動下的相對運動狀態，則其他攝動下的相對運動狀態只需通過攝動項的疊加即可得到。得出周期性相對運動條件后，用時域配點法和列文伯格-馬夸爾特法(LM)對該條件的初值求解，可得到不消耗任何燃料的周期性繞飛軌道。

1 橢圓參考軌道相對運動建模

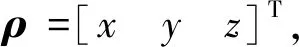
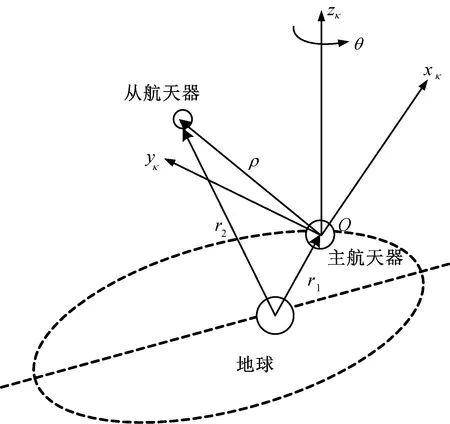
圖1 旋轉Euler-Hill參考坐標系示意圖Fig.1 Schematic diagram of rotating Euler-Hill reference coordinate system

建立拉格朗日函數[9]，設主航天器在任意橢圓軌道上運動，考慮活動坐標系之間的相對導數關系，可得從航天器的速度

(1)

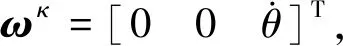
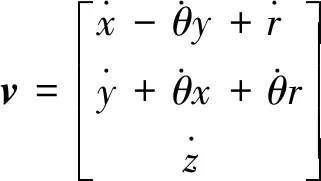
(2)

動能表示為

(3)

勢能Ep(先只考慮正常引力勢)為

Ep= -μ/‖r2‖=-μ/‖r1+ρ‖=

(4)

式中：μ為地球引力勢；Pk(cosα)為勒讓德多項式,其中,

(5)

從而得拉格朗日函數

(6)

只取正常引力勢中的第1，2階可得

(7)

哈密爾頓系統的正則動量(px,py,pz)為

(8)

(9)

由式(9)可見，哈密爾頓函數不顯含時間t，則根據哈密爾頓動力學原理可知，HJ方程有如下形式，即

(10)

考慮由(q,p)→(β,α)的正則變換，其中，q,p,β,α為正則變量。S為雅可比完全積分，其形式一般為

S=W(q1,q2,…,qf;α1,α2,…,αf)-

E(α1,α2,…,αf)t

(11)

式中：W(q1,q2,…,qf;α1,α2,…,αf)為哈密頓特征函數，(q1,q2,…,qf)為廣義坐標；E(α1,α2,…,αf)為不含時間t的函數，(α1,α2,…,αf)為積分常數；t為時間；f為系統的自由度。則正則變換表示為

(12)

系統自由度f現為3，令式(11)中E(α1,α2,…,αf)=-α′1，則可得雅可比完全積分S為

(13)

從而可將HJ方程表示為W(x,y,z)的偏微分方程，即

(14)

將z方向單獨分離出來，W(x,y,z)=W′(x,y)+W3(z)，則HJ方程變為

(15)

(16)

將式(15)積分得

(17)

再令

(18)

同時令

(19)

由式(19)可得

(20)

(21)

積分得

W1(x)=

(22)

因此，可將雅可比完全積分S表示為

(23)

(24)

(25)

(26)

再根據正則變換式(12)可得βi，經過一系列化簡和小量忽略可得表達式

(27)

(28)

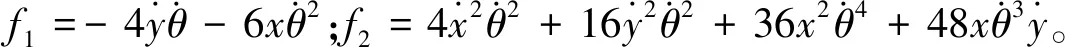
再聯立式(24)，(26)，(27)，(28)，解出x(t)，y(t)關于α1，β1，α3，β3的表達式，經化簡后可得

(29)

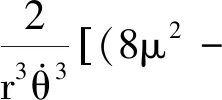
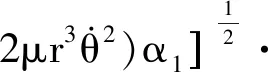
(30)

由此可得x，y方向上的運動形式與正則變量α1，β1，α3，β3的關系。如已知α1，β1，α3，β3的函數表達式，就可得到x(t)和y(t)的表達式，從而可知從航天器相對于主航天器在x-y平面內的運動模式。

由上文推導過程可知，z方向的運動和x，y方向是完全解耦的。可先研究x-y平面內的運動特性，再通過分別控制x-y平面的運動和z方向的運動得到三維空間的運動模式。因此，本文主要針對x-y平面內的運動特性進行分析，未專門對z方向上的運動進行研究。

以上推導都是基于正常引力勢的第1，2階項得出，將此時得到的哈密爾頓函數(9)記為H(0)，當考慮引力勢的更高階項或J2項時，將哈密爾頓函數記作H=H(0)+H(1)+H(2)+…+H(n)。其中，H(1)，H(2)，…，H(n)是考慮攝動或非線性引力勢附加的哈密爾頓函數ΔH，其被稱為攝動哈密爾頓函數，即ΔH=H(1)+H(2)+…+H(n)。

當考慮攝動時，由哈密爾頓理論可能較難得出相對運動的顯示解析表達式，但無攝情況下的運動模型已精確得到，即式(29)，(30)。因此，根據正則攝動理論，當ΔH很小時，可對無攝條件下得到的動力學模型作適當修正，從而得到攝動下動力學模型的近似解。

將不考慮攝動情況下精確的哈密爾頓函數記作H0(p,q,t)，則可將雅可比完全積分S(q,α,t)作為廣義函數，得到從(q,p)→(β,α)的正則變換，且變換后的新的哈密爾頓函數為零，則(β,α)是一組與時間無關的正則變量，由此可以得出相應的在無攝情況下關于模型的精確解。當考慮攝動時，將哈密爾頓函數寫成

H(p,q,t)=H0(p,q,t)+ΔH(p,q,t)

(31)

考慮到對于給定坐標變換的正則性與哈密爾頓函數的具體形式無關，因此，由S(q,α,t)作為廣義函數而產生的正則變換(q,p)→(β,α)在攝動條件下還是一組正則變換，只是在攝動下得到的新哈密爾頓函數將不再為零，新的正則變量(β,α)也不再是與時間無關的變量。新哈密爾頓函數的形式為

(32)

因此，正則變量滿足關系式

(33)

(34)

求解上述2f個方程(f為自由度，本文有4個自由度)，得到αi，βi關于時間的函數表達式，則由(q,p)→(β,α)的變換，可得相應的qi，pi關于時間的表達式，從而得到動力學模型。

將上述理論運用到考慮非線性引力勢第3，4階，以及J2項的建模中。非線性引力勢第3階的攝動哈密爾頓函數可表示為

(35)

非線性引力勢第4階的攝動哈密爾頓函數可表示為

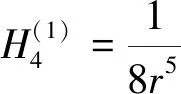
24μx2y2+24μx2z2-6μy2z2)

(36)

考慮J2攝動項的攝動哈密爾頓函數為

(37)

式中：Z=(r+x)sinisinθ+ysinicosθ+zcosi；引力常數μ=3.960 05×105km3/s2；地球赤道平均半徑Re=6 378.140 km；帶諧系數J2=0.001 082 63；i為參考軌道傾角；θ為真近點角。

將上述攝動哈密爾頓函數代入求解后可得αi(t)，βi(t)關于時間t的表達式，再代入(q,p)→(β,α)變換關系式中，即式(29)，(30)中，可得x(t)和y(t)在攝動情況下的表達式，即攝動情況下的模型為

(38)

y(t)=-3α3(t)(t+β1(t))+β3(t)+

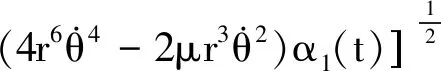
(39)

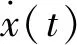
(40)

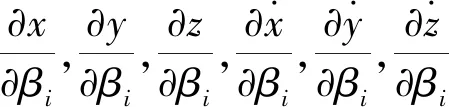
綜上，求解攝動情況下的動力學模型只需求解一組非線性方程組，即

(41)

(42)

則可得動力學方程(38)，(39)。

2 周期性相對運動條件

橢圓基準軌道的動力學模型為式(38)，(39)，經分析不難發現，獲得周期為T的周期性相對運動的條件為：?t滿足關系式

α1(t)=α1(t+T)

(43)

α3(t)=α3(t+T)

(44)

f1(t)=β3(t)-3α3(t)(β1(t)+t),

f1(t)=f1(t+T)

(45)

即

α1(t)=α1(t+T)

(46)

α3(t)=α3(t+T)

(47)

β1(t)=β1(t+T)

(48)

(49)

3 周期性相對運動初始化條件求解

將周期條件截斷為含有N項的傅里葉級數的形式，即

(50)

(51)

(52)

(53)

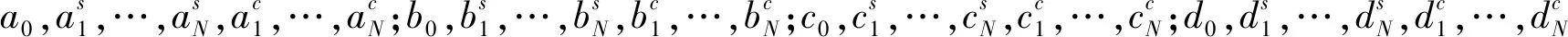
(54)

則周期性相對運動的初值條件為

(55)

(56)

(57)

(58)

時域配點法是一種非線性系統的求解方法。它將常微分方程組轉化為非線性代數方程組，再用其他求解非線性代數方程組的方法對得到的方程組進行求解，避免了直接求解常微分方程組，對于周期解的處理十分有效。該方法在文獻[10-11]中被提出，本文不對此作詳細說明。

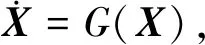
(59)

利用時域配點法進行相應變換，式(59)左端有

(60)

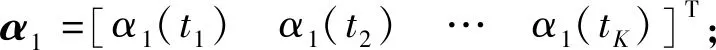
因此，微分方程組轉化后的非線性代數方程組表示為

(61)

求解該非線性代數方程組，可得4×(2N+1)個配點的值，有

(62)

(63)

由此可求得4×(2N+1)個傅里葉系數，將其代入式(55)，(56)，(57)，(58)可得周期運動初值。

采用LM方法對式(61)的非線性代數方程組

(64)

(65)

進行求解，可避免采用牛頓-拉斐森迭代法(NR)進行求解時由于方程形式過于復雜，雅可比矩陣出現奇異或病態嚴重，無法繼續迭代的情況。

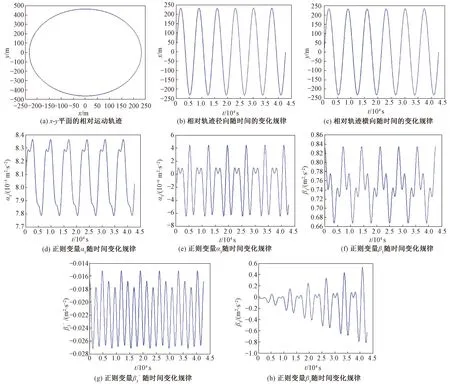
圖2 參考橢圓軌道偏心率為0.02仿真結果Fig.2 Simulation results of elliptical orbit with eccentricity of 0.02

采用一種全局收斂的LM算法[12-15]，考慮矢量形式的非線性方程組F(x)=0。利用線性方程組的解dk作為在點xk上的一個搜索方向：((Jk)T·Jk+μkI)dk=-(Jk)TFk。其中，I為單位矩陣，Jk為雅可比矩陣。通過引進非負參數μk可保證矩陣((Jk)TJk+μkI)非奇異，同時也能避免出現過大的‖dk‖。同時，對于迭代步((Jk)TJk+μkI)dk=-(Jk)TFk，選取參數μk=αk(θ‖Fk‖+(1-θ)‖(Jk)TFk‖),θ∈[0,1]。其中，對于參數αk的選取采用信賴域技巧來修正。定義價值函數φ(x)=‖F(x)‖2，第k步迭代的實際下降量Ak=‖Fk‖2-‖F(xk+dk)‖2,預估下降量Pk=‖Fk‖2-‖Fk+Jkdk‖2，實際下降量與預估下降量的比值rk=Ak/Pk，由此來決定是否接受試探步dk和調整迭代過程中αk因子的大小。rk越大，表明目標函數φ(x)=‖F(x)‖2下降越多，則接受dk，同時希望下一試探步dk+1更長，故減小αk；反之，rk越小，則拒絕dk，同時增大αk。

4 仿真算例

對考慮正常引力勢的非線性3，4階項進行仿真，取橢圓參考軌道長半軸a=8 000 km，過近地點時刻tp=0，偏心率e=0.02，其余3個軌道根數均取為0，將傅氏級數截斷為N=3，在一個周期上均勻地取7個配點，仿真6個軌道周期，結果如圖2所示。

為定量描述每個周期的軌道漂移量的大小，以衡量周期運動的好壞，引入如下指標來粗略描述經過一個周期T的漂移量，即

(66)

經計算可得ΔT=0.315 9 m。由此可見：每過一圈的漂移量是很小的。這充分說明周期條件初值在用于軌道計算時能保持較好的周期性，在軌道保持和控制等方面具有工程應用價值。仿真結果驗證了模型和求解方法的有效性。

5 結束語

本文主要基于哈密爾頓力學建立橢圓參考軌道的相對運動模型，利用正則攝動理論將哈密爾頓函數分解為線性項和攝動項。線性項的精確解很容易得到，攝動項則可通過線性項的修正獲得，且各攝動項滿足線性疊加的特點，各種軌道攝動和人為控制易于加到運動模型中。同時，針對模型特點推導了周期性相對運動條件，利用時域配點法和LM方法對周期性相對運動的初始值進行求解，得到了不消耗任何燃料的周期性繞飛軌道，為空間交會、編隊飛行、機動伴飛等航天領域的研究提供了有益參考。