基于神經(jīng)網(wǎng)絡的直升機適航噪聲預估方法研究

仲唯貴

(中國直升機設計研究所，江西 景德鎮(zhèn) 333001)

0 引言

民用直升機用途廣泛，執(zhí)行任務時往往要在人口稠密的城市中心地帶起降和飛行，以完成緊急醫(yī)療服務、城市消防、治安維護等任務。直升機較高的外部噪聲水平直接影響城區(qū)居民的生活環(huán)境，城市中往往會采取限制直升機在城區(qū)運輸?shù)娘w行路線和飛行時間的措施，以保證城區(qū)良好的生活環(huán)境，這成為阻礙直升機在城區(qū)服務和商業(yè)應用中發(fā)展的重要環(huán)節(jié)。因此國內(nèi)外的民用航空適航規(guī)定中，都對直升機的噪聲水平進行了嚴格的限定[1]。

在民用直升機的設計中，直升機的適航噪聲水平分析是重要的設計流程。為進行直升機外部噪聲的分析，研究人員建立了基于CFD技術和FW-H聲學方程的直升機氣動噪聲計算方法，并開發(fā)了眾多的分析程序[2-4]。但是利用這些方法進行直升機適航噪聲計算需要大量詳細的數(shù)據(jù)，需要考慮旋轉(zhuǎn)噪聲、脈沖噪聲和寬帶噪聲等噪聲成分，同時要進行適航狀態(tài)的飛行模擬給出配平結果，需要復雜的分析模型和較長計算周期。因此，建立高效的直升機適航噪聲分析方法對民用直升機的設計具有重要意義。

本文考慮直升機外部噪聲的主要影響因素，基于神經(jīng)網(wǎng)絡模型建立了簡單有效的直升機適航噪聲分析方法，用于直升機適航噪聲的快速分析。

1 直升機適航狀態(tài)噪聲分析問題描述

民用直升機的研發(fā)必須滿足噪聲適航規(guī)范(CCAR-36)的要求。直升機噪聲水平在CCAR36部中有明確規(guī)定，包含了三種飛行狀態(tài)：起飛狀態(tài)、飛越狀態(tài)和進場狀態(tài)[5]。適航規(guī)范對直升機三種飛行狀態(tài)的飛行高度、速度、過程以及噪聲數(shù)據(jù)的處理進行了嚴格規(guī)定，并以重量為函數(shù)給出了相應的噪聲水平限定要求(圖1)。

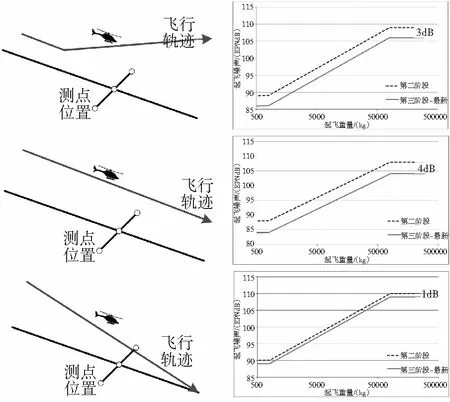
圖1 直升機適航噪聲要求

在民用直升機的研發(fā)過程中，適航噪聲水平分析是基本的設計流程(圖2)。根據(jù)直升機的設計參數(shù)，建立三種適航狀態(tài)的計算分析模型，實現(xiàn)直升機噪聲水平計算。進行精確的直升機適航噪聲分析，要完成飛行狀態(tài)的配平計算、載荷計算以及聲學計算等流程，需要的計算參數(shù)多，計算周期長。本文在提煉直升機噪聲的主要影響參數(shù)基礎上，利用神經(jīng)網(wǎng)絡適用于非線性預估的特點，采用美國聯(lián)邦航空局(FAA)的資訊通報發(fā)布的直升機適航噪聲飛行試驗數(shù)據(jù)[6]，進行神經(jīng)網(wǎng)絡的設計和訓練，建立基于神經(jīng)網(wǎng)絡的直升機適航噪聲分析方法。方法可用于概念設計和方案設計階段的直升機適航噪聲分析以及總體參數(shù)的優(yōu)化，并且隨著大量的試驗和試飛數(shù)據(jù)的積累，可進一步完善神經(jīng)網(wǎng)絡模型，實現(xiàn)直升機噪聲的準確預估。

圖2 直升機適航噪聲預估流程

2 神經(jīng)網(wǎng)絡模型及模型訓練

基于神經(jīng)網(wǎng)絡模型進行直升機適航噪聲水平分析是應用神經(jīng)網(wǎng)絡模型的非線性函數(shù)近似功能，獲得給定參數(shù)的直升機適航噪聲水平。應用神經(jīng)網(wǎng)絡模型進行函數(shù)近似的主要優(yōu)點是通過訓練數(shù)據(jù)能夠獲得網(wǎng)絡輸入和輸出的高度非線性關系，設計的網(wǎng)絡能夠適用于新的數(shù)據(jù)，并且保證誤差在有限的范圍內(nèi)，同時網(wǎng)絡輸入和設計參數(shù)的合理選擇能夠保證神經(jīng)網(wǎng)絡模型的魯棒性[7]。

2.1 神經(jīng)網(wǎng)絡模型

本文建立了五層結構的反向傳播(BP)神經(jīng)網(wǎng)絡模型，中間層為3層，輸出為3項，其中為xi為神經(jīng)網(wǎng)絡輸入，yi為神經(jīng)網(wǎng)絡實際輸出(見圖3)。

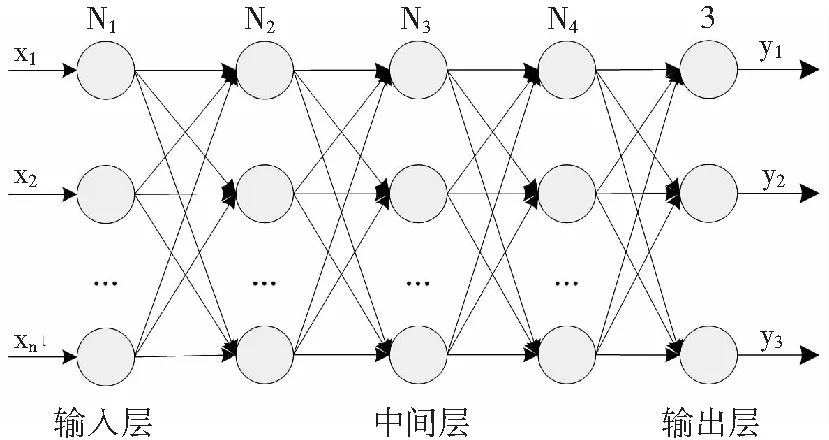
圖3 神經(jīng)網(wǎng)絡模型

神經(jīng)網(wǎng)絡的數(shù)學模型表示如下。隱蔽層第j個神經(jīng)元的輸入為：

netj=∑iωjiOi

(1)

其中：ωji為第j個神經(jīng)元的權值，Oi為輸入層第i個神經(jīng)元輸出。

第j個神經(jīng)元的輸出為：

Oj=f(netj)

(2)

其中：f()為激勵函數(shù)，采用雙曲正切函數(shù)，表示為：

(3)

神經(jīng)網(wǎng)絡訓練涉及迭代優(yōu)化神經(jīng)元權重和偏差，提升網(wǎng)絡的性能，通過測量訓練網(wǎng)絡的輸出與期望輸出的誤差評估網(wǎng)絡性能。本文采用神經(jīng)網(wǎng)絡容差的均方值作為網(wǎng)絡性能的度量。

(4)

其中：tk是目標輸出，Ok是神經(jīng)網(wǎng)絡輸出。

2.2 神經(jīng)網(wǎng)絡的訓練

為保證神經(jīng)網(wǎng)絡具有較好的通用性，能夠有效模擬不在訓練序列中的輸入數(shù)據(jù)，訓練網(wǎng)絡時采用了提前停止法。有效數(shù)據(jù)的一部分用于訓練網(wǎng)絡，另一部分用于驗證網(wǎng)絡的訓練結果。在訓練迭代的每一步，神經(jīng)網(wǎng)絡模擬驗證序列中的輸入數(shù)據(jù)并計算MSE，驗證序列的容差會隨著訓練序列的容差下降，但是隨著神經(jīng)網(wǎng)絡的訓練達到過擬合，驗證序列的容差開始增加，此時訓練停止并且認為神經(jīng)網(wǎng)絡訓練達到了較優(yōu)的性能。

訓練和驗證序列中的數(shù)據(jù)數(shù)量和構成對神經(jīng)網(wǎng)絡的訓練有重要影響。在研究中，所有數(shù)據(jù)的近80%用于訓練，20%用于驗證。為避免訓練序列和驗證序列中數(shù)據(jù)的傾向性，進行序列構建時進行數(shù)據(jù)隨機分配構建多組方案的序列，訓練多組神經(jīng)網(wǎng)絡，用于神經(jīng)網(wǎng)絡性能的橫向?qū)Ρ取Ｓ捎谟柧氶_始前神經(jīng)元的初始權重和誤差是隨機給出的，對神經(jīng)網(wǎng)絡的每次訓練都會對最終性能產(chǎn)生一點差別，所以采用多組神經(jīng)網(wǎng)絡訓練可以更好地評估訓練的神經(jīng)網(wǎng)絡的性能。每組神經(jīng)網(wǎng)絡訓練10次直到提前停止發(fā)生，通過MSE的平均值進行判定。

3 直升機適航噪聲分析設計參數(shù)影響分析

直升機適航噪聲水平受到起飛重量、旋翼和尾槳參數(shù)的影響，考慮到神經(jīng)網(wǎng)絡的性能受到輸入?yún)?shù)的影響較大，合理選擇輸入?yún)?shù)會使神經(jīng)網(wǎng)絡產(chǎn)生較好的性能和對新數(shù)據(jù)的適應性。為了分析神經(jīng)網(wǎng)絡性能隨輸入?yún)?shù)的變化，進行了參數(shù)化的影響研究。用于直升機適航噪聲預估的神經(jīng)網(wǎng)絡的輸入?yún)?shù)選擇范圍在表1中給出，完整的全局輸入共含10個參數(shù)。

表1 計算輸入?yún)?shù)選擇

根據(jù)輸入?yún)?shù)，制定了四組輸入?yún)?shù)序列：

(1)序列1：W、Dm、Vtm、σm、Nm

(2)序列2：W、Dm、Vtm、σm、Nm、P

(3)序列3：W、Dm、Vtm、σm、Nm、Dt、Vtt、σt、Nt

(4)序列4：W、Dm、Vtm、σm、Nm、Dt、Vtt、σt、Nt、P

第一組輸入?yún)?shù)序列包含了5個參數(shù)，主要針對起飛重量和旋翼參數(shù)；第二組輸入?yún)?shù)序列在第一組的基礎上增加了起飛功率；第三組輸入?yún)?shù)序列包含了9個參數(shù)，主要針對起飛重量、旋翼和尾槳參數(shù)；第四組輸入?yún)?shù)序列包含了所有的10個參數(shù)。

以四組不同的設計輸入對神經(jīng)網(wǎng)絡進行訓練和確認，每組訓練10次，并取10次訓練網(wǎng)絡性能的平均值，通過對比研究不同輸入?yún)?shù)對直升機適航噪聲預估神經(jīng)網(wǎng)絡的性能的影響，結果在圖4中給出。

圖4 采用不同輸入?yún)?shù)的神經(jīng)網(wǎng)絡性能

從圖中可以看出，采用四組輸入?yún)?shù)進行神經(jīng)網(wǎng)絡訓練，都能獲得性能較好的神經(jīng)網(wǎng)絡,但是采用全部輸入?yún)?shù)訓練的神經(jīng)網(wǎng)絡性能最優(yōu)，說明訓練的神經(jīng)網(wǎng)絡能夠反映直升機總體參數(shù)對適航噪聲的影響。

4 直升機適航噪聲預估模型訓練結果

以10個參數(shù)為輸入，利用訓練的性能較優(yōu)的神經(jīng)網(wǎng)絡，對飛越狀態(tài)、起飛狀態(tài)和進場狀態(tài)三個適航狀態(tài)的直升機噪聲水平進行了對比，評估神經(jīng)網(wǎng)絡的直升機適航噪聲預測水平，結果見圖5至圖7。圖中包含了用于訓練和試驗的所有數(shù)據(jù)，試驗數(shù)據(jù)從所有數(shù)據(jù)中隨機選擇，不低于總數(shù)據(jù)的20%。圖5給出了飛越狀態(tài)直升機噪聲的預測值與測試值的對比，可以看出神經(jīng)網(wǎng)絡的預測值與測試值具有較好的一致性，線性相關系數(shù)R=0.965；從預測結果的誤差帶來看，低于2EPNdB。圖6給出了起飛狀態(tài)直升機噪聲的預測值與測試值的對比，可以看出神經(jīng)網(wǎng)絡的預測值與測試值一致性較好，線性相關系數(shù)R=0.947；從誤差帶來看，僅有一個點的噪聲預測值與測試值偏差較大，接近2.5EPNdB。圖7給出了進場狀態(tài)直升機噪聲的預測值與測試值的對比，可以看出神經(jīng)網(wǎng)絡的預測值與測試值一致性較好，線性相關系數(shù)R=0.929；從誤差帶來看，僅有一個點的噪聲預測值與測試值偏差較大，超出了2EPNdB。從三種狀態(tài)的線性相關系數(shù)變化來看，飛越狀態(tài)的直升機噪聲預測結果最好，起飛和進場狀態(tài)的預測結果偏差較大，主要是由于起飛和進場狀態(tài)的直升機噪聲成分更復雜，其準確分析需要更詳細的輸入?yún)?shù)，并建立更復雜的神經(jīng)網(wǎng)絡。

圖5 直升機飛越噪聲預估結果

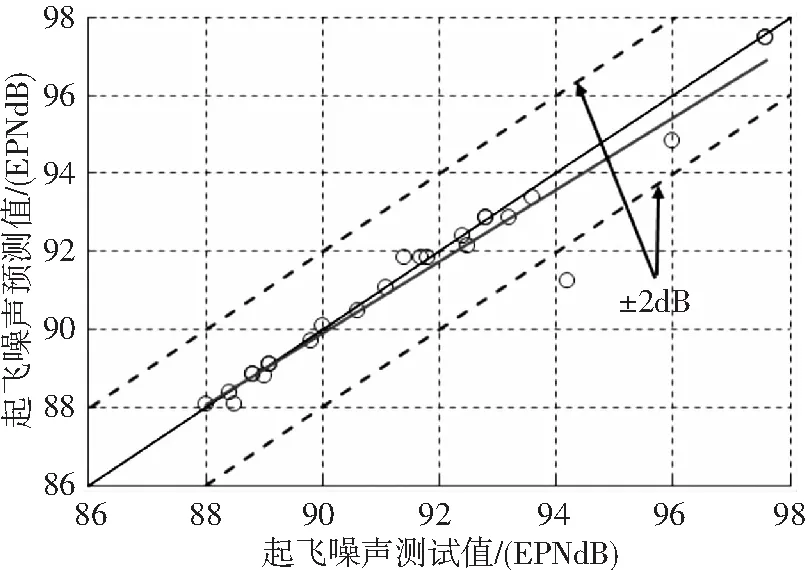
圖6 直升機起飛噪聲預估結果

圖7 直升機進場噪聲預估結果

5 結論

本文以直升機適航噪聲的預估方法為研究對象，進行了基于神經(jīng)網(wǎng)絡的直升機適航噪聲預估方法研究，建立直升機適航噪聲預測神經(jīng)網(wǎng)絡模型，并進行了神經(jīng)網(wǎng)絡的測試和評估，主要結論如下：

1)基于神經(jīng)網(wǎng)絡模型，利用直升機適航噪聲的飛行試驗數(shù)據(jù)，采用合理的訓練方法，能夠訓練出有效預估直升機適航噪聲的神經(jīng)網(wǎng)絡模型；

2)以直升機起飛重量、旋翼和尾槳的主要參數(shù)為輸入，通過訓練的神經(jīng)網(wǎng)絡模型，能夠進行直升機適航噪聲的有效預估；

3)對直升機適航噪聲預估結果的分析表明，通過對神經(jīng)網(wǎng)絡的有效訓練，能夠使直升機適航噪聲的預估結果誤差小于2.5EPNdB。