基于分形特征和ILST-KSVC的調(diào)制方式識別
張子, 羅正華,陳紹祥
(1.電信科學(xué)技術(shù)第五研究所,四川 成都 610062; 2.成都大學(xué) 信息科學(xué)與工程學(xué)院,四川 成都 610106)
0 引 言
數(shù)字調(diào)制信號的識別,是指在未知接收信號信息的前提下判斷出數(shù)字信號的調(diào)制方式,從而為下一步進(jìn)行信號的解調(diào)處理提供所需信息.如何在復(fù)雜多變的環(huán)境下高效地識別出不同調(diào)制方式的信號,科研人員提出了不同的解決方案[1-3].在此基礎(chǔ)上,本研究提出了一種基于分形理論及多分類最小二乘雙支持向量機(jī)(Least squares twin multi-class classification support vector machine,ILST-KSVC)分類器[4-5]的數(shù)字信號調(diào)制識別方法.仿真測試結(jié)果表明,與傳統(tǒng)的數(shù)字調(diào)制信號識別方法相比,本識別方法具有信號識別率更高且識別性能更好的優(yōu)點,并能夠有效提高信號識別的抗干擾能力.
1 數(shù)字調(diào)制信號的分形特征提取
分形維數(shù)是分形理論研究中的一個重要內(nèi)容,而通信信號作為一種時間序列,利用分形維數(shù)就能夠區(qū)分信號的不規(guī)則程度.分形維數(shù)中的盒維數(shù)描述了分形集的幾何尺度情況,而信息維數(shù)描述了分形集在區(qū)域空間上的分布信息,故本研究結(jié)合這2種維數(shù)作為通信信號調(diào)制方式識別的特征參數(shù).
1.1 分形盒維數(shù)
假設(shè)有集合C是Rn空間中的任一有界非空子集,那么對于任何ε>0,N(f,ε)可看作中心為f、最大直徑為ε且能完全覆蓋集合C的最小數(shù)目,如果存在,
(1)
則稱DB為C的盒維數(shù).實際應(yīng)用中,可根據(jù)不同需要采用球、線段或立方體等作為盒.
1.2 分形信息維數(shù)
由于盒維數(shù)只能對空間內(nèi)的幾何尺度情況進(jìn)行表達(dá),而不能反映集合在平面空間上的分布疏密,故引入信息維數(shù)的概念進(jìn)行補(bǔ)充.
設(shè){Aj,j=1,2,3,…,K}是集合C的一個有限ε-格形覆蓋,同時設(shè)Pj表示C的元素落在集合Aj中的概率,則有信息熵,
(2)
且信息熵滿足以下關(guān)系[6],
I(ε)~-lgεDI(f)
(3)
式中,DI(f)是集合C的信息維數(shù),其表達(dá)式為,
(4)
不同尺度分解下的調(diào)制信號的盒維數(shù)和信息維數(shù)包含了不同調(diào)制信號之間幅度、頻率和相位的區(qū)別,因此可將所提取的信號分類特征用盒維數(shù)和信息維數(shù)表征為,
T=[DB(f),DI(f)]
(5)
根據(jù)文獻(xiàn)[7]對分形特征在不同噪聲環(huán)境下特征性能的分析得出,在一個恰當(dāng)?shù)腟NR以上時,各種噪聲對特征的影響比較緩慢,能有效保證分類特征在決策空間內(nèi)存在一個較為清晰的界限.
2 基于ILST-KSVC的分類器設(shè)計
目前,在機(jī)器學(xué)習(xí)中所使用的大部分分類算法都基于多分類支持向量回歸機(jī)(Support vector machine for multi-class classification,KSVCR),該支持向量機(jī)能直接對三分類問題求解,對多分類的問題有很好的分類效果.其中,ILST-KSVC[8-9]就是在KSVCR的基礎(chǔ)上加以改進(jìn)而成,其結(jié)構(gòu)更加簡單,運算速率更快,大大改善了處理多分類問題時的訓(xùn)練速度和準(zhǔn)確率.
在醫(yī)學(xué)統(tǒng)計學(xué)教學(xué)全部完成后,利用課間進(jìn)行調(diào)查,采用無記名、自填問卷、當(dāng)場回收方式開展調(diào)查。由醫(yī)學(xué)統(tǒng)計學(xué)教師發(fā)放問卷,組織學(xué)生填寫。問卷內(nèi)容包括個人基本信息、對醫(yī)學(xué)統(tǒng)計學(xué)教學(xué)效果的評價、各章節(jié)教學(xué)內(nèi)容難易度評價、個人學(xué)習(xí)效果自我評價及教學(xué)建議。
2.1 “一對一對余”方法
“一對一對余”方法就是將支持向量回歸機(jī)與傳統(tǒng)的標(biāo)準(zhǔn)支持向量分類機(jī)進(jìn)行結(jié)合,從而達(dá)到對三分類問題求解的目的.
假定一個三分類的訓(xùn)練集P={(x-n,y-n)|n=1,2,…,k},其中,
(6)
使矩陣E?Rk1×m表示標(biāo)簽分類是+1的訓(xùn)練樣本,矩陣F?Rk2×m表示分類標(biāo)簽為-1的訓(xùn)練樣本,矩陣G?Rk3×m是屬于其他分類的訓(xùn)練樣本,用標(biāo)簽0表示.其中,k是訓(xùn)練樣本數(shù)據(jù)的總和,且k=k1+k2+k3.
對于D類的多分類情況,選取訓(xùn)練數(shù)據(jù)中的第i、j(i≠j)類作為數(shù)據(jù)樣本中的正、負(fù)類,其余的D-2類作為0類,則將這種方法稱作“一對一對余”.本方法對全部i、j類進(jìn)行訓(xùn)練后獲得D(D-1)/2個三分類器,即得到對應(yīng)的D(D-1)/2個判決函數(shù)的輸出,并利用“投票法"完成了對全部測試樣本所屬類別的判定,規(guī)則如下:對分類標(biāo)簽未知的樣本α,如果在經(jīng)過決策函數(shù)判別后輸出為1,記作α為正類,投第i類1票;與此相反,如果在經(jīng)過決策函數(shù)判別輸出為-1,則將α記作負(fù)類,投第j類1票;如果判決函數(shù)輸出為0時,不進(jìn)行投票.所有D(D-1)/2次投票完成后,對投票結(jié)果進(jìn)行計算,最終取α為得票數(shù)最多的測試樣本.若2種投票數(shù)相同時,只需任選其中1種作為投票最終結(jié)果.根據(jù)投票規(guī)則可以看到,此類結(jié)構(gòu)的分類器分類準(zhǔn)確率更高且效果更明顯.
2.2 基于ILST-KSVC的信號調(diào)制識別系統(tǒng)架構(gòu)設(shè)計
數(shù)字信號對時效性的要求比較高,所以要求算法訓(xùn)練時間盡量短.目前應(yīng)用在數(shù)字調(diào)制信號識別的常用方法有:判決樹、高階積累量、概率神經(jīng)網(wǎng)絡(luò)(Probabilistic neural network,PNN)及支持向量機(jī)(Support vector machine,SVM)等.本研究將ILST-KSVC應(yīng)用到數(shù)字信號調(diào)制方式識別的問題上,針對CW、2ASK、4ASK、2FSK、4FSK、2PSK、4PSK與16QAM共8種調(diào)制方式進(jìn)行識別仿真.識別流程架構(gòu)設(shè)計如圖1所示.
圖1系統(tǒng)架構(gòu)設(shè)計流程圖
3 模擬結(jié)果及分析
為驗證所提出的方法的有效性,本研究將各種數(shù)字調(diào)制信號混雜并加入噪聲作為接收到的信號來設(shè)計仿真實驗,選擇的信號包括未調(diào)載波CW及已調(diào)信號2ASK、4ASK、2FSK、4FSK、2PSK、4PSK、16QAM共8種數(shù)字信號.本研究對每種調(diào)制信號類型在-5、0、5、10及15 dB時分別采用120個樣本進(jìn)行訓(xùn)練,再用1 200個樣本進(jìn)行測試.其中:實驗1對8種不同的調(diào)制方式提取了分形盒維數(shù)和信息位數(shù)作為提取的信號調(diào)制特征;實驗2測試了在不同信噪比的條件下本研究提出的ILST-KSVC分類器與傳統(tǒng)分類器對8種數(shù)字信號調(diào)制方式的識別效果.
實驗的取樣頻率為80 kHz,選用的接收機(jī)帶寬為20 kHz,中頻為10 MHz.已調(diào)信號的信號碼元速率為1 200 bit/s,其中BFSK和QFSK信號的頻偏分別為5和2.5 kHz.本研究使用MATLAB R2016a編程完成仿真.
3.1 2種分形特征的均值和方差
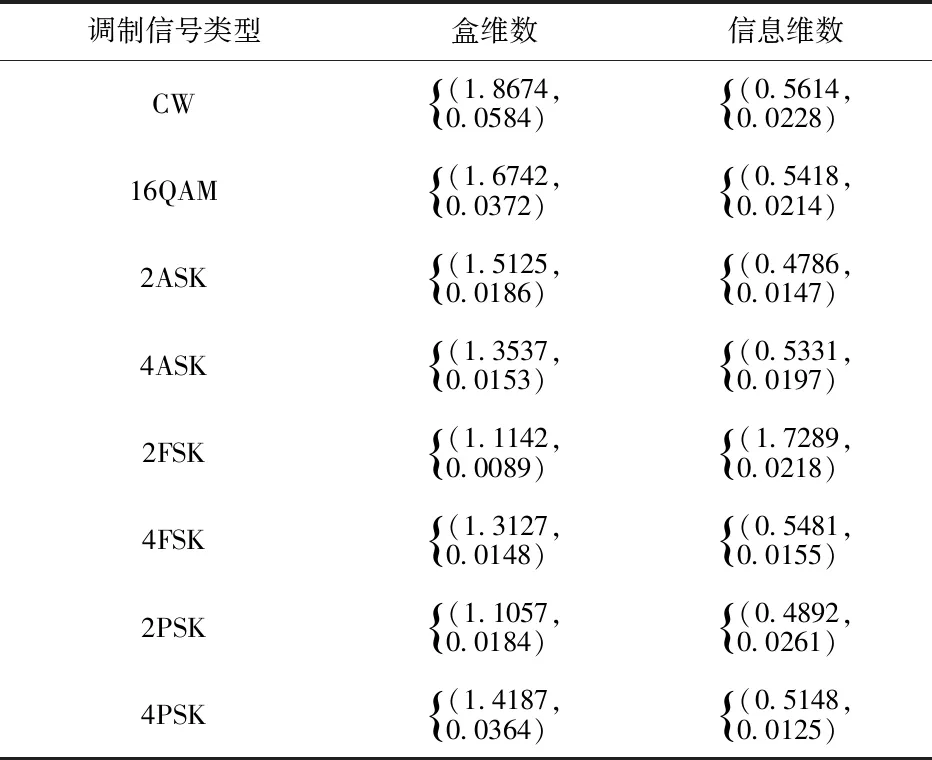
MATLAB仿真定量給出了如下表1所示每種信號在-5~15 dB的SNR范圍內(nèi)分形盒維數(shù)及信息維數(shù)的均值和方差.
數(shù)字調(diào)制信號分形特征的均值表明其特征空間中的位置與中心點的偏離程度,較小的方差說明在中心點處特征的聚集成度非常高,而分形特征的方差又能有效地表明不同信號特征之間的內(nèi)部波動程度.本研究通過將這2種分形特征組合成特征向量來實現(xiàn)對差異信息的描述.從每類的每個SNR點上取50個特征樣本, 總共2 000個,的特征分布圖.
制作出如圖2所示
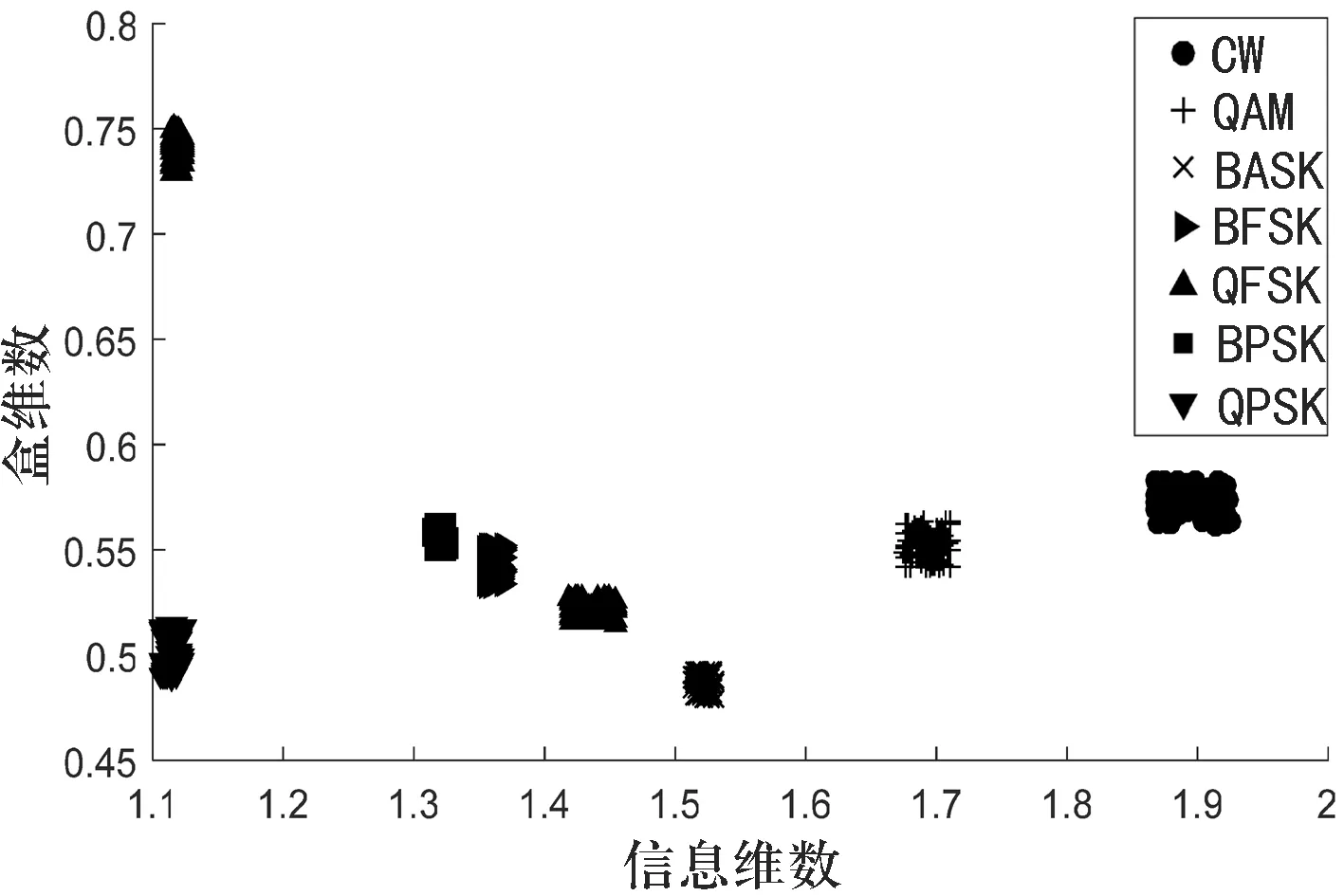
圖2信息維數(shù)與盒維數(shù)的聯(lián)合特征分布圖
從圖2可知,本研究通過提取數(shù)字調(diào)制信號的分形維數(shù)的聯(lián)合特征,能有效地對每種調(diào)制方式進(jìn)行區(qū)分,為下一步調(diào)制信號的分類提供了很好的支持.
3.2 不同分類器仿真性能測試
針對已提取的2種分形維數(shù)組合成的特征向量,本研究完成了SVM、PNN、ILST-KSVC 3種分類器分類性能的測試.測試過程中,每次只對某種調(diào)制方式進(jìn)行識別,結(jié)果如表2所示.

表2 不同分類器的識別效果/%
從表2結(jié)果可知,針對同種調(diào)制方式而言,不同分類器的識別率也有所不同,在低信噪比的條件下,PNN分類器要比SVM分類器對數(shù)字信號調(diào)制方式的識別率高,而ILST-KSVC分類器識別率最優(yōu).
同時,本研究進(jìn)一步做了以下2組實驗,以測試不同分類器的識別性能.
1)實驗1.不同信噪比環(huán)境下,3種算法的分類識別率對比.
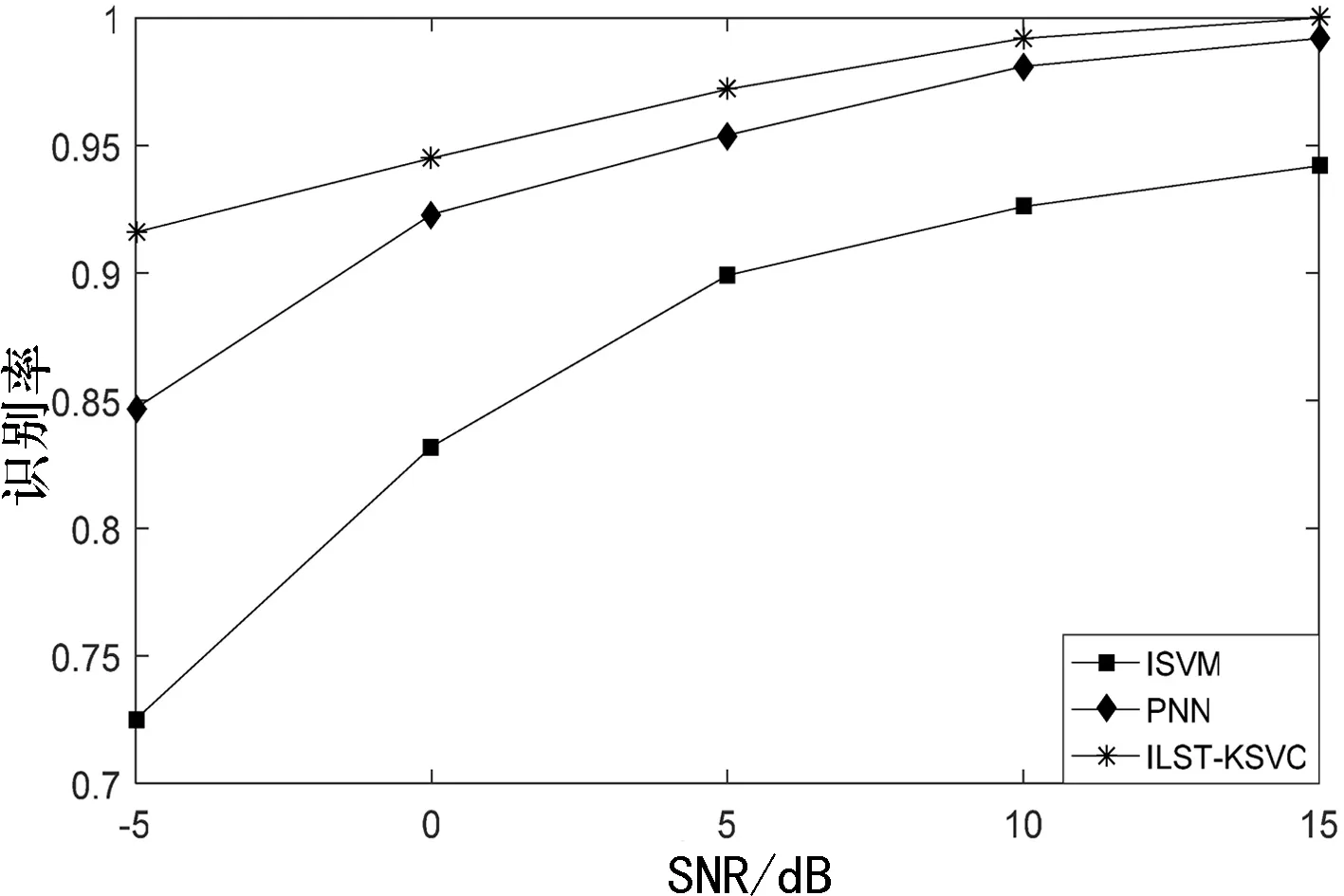
圖3不同信噪比下3種算法識別率對比圖
從圖3可知:基于3種算法的分類器對調(diào)制信號的識別率都隨著信噪比的增加而增加,且在5 dB之后識別率漸漸趨于平穩(wěn);基于ILST-KSVC分類器的識別率明顯優(yōu)于PNN及ISVM分類器,其識別性能最優(yōu).
2)實驗2.當(dāng)信噪比固定在5 dB時,3種算法訓(xùn)練耗時對比.
信噪比在5 dB的環(huán)境下,3種算法分類器對調(diào)制信號識別所需的訓(xùn)練時間,如圖4所示.
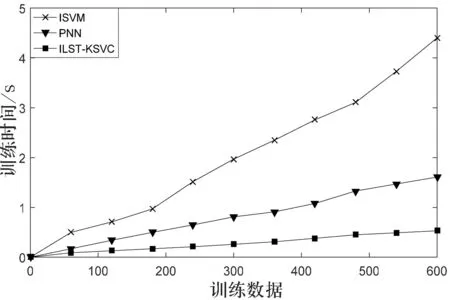
圖4信噪比在5 dB時不同算法訓(xùn)練耗時對比
從圖4可知:當(dāng)信噪比固定在5 dB時,基于ILST-KSVC算法的分類器在計算過程中所需要的時間明顯要少于基于PNN算法分類器及ISVM算法分類器.
此外,本研究通過實驗仿真了在信噪比從-5到15 dB時ILST-KSVC分類器對8種數(shù)字調(diào)制方式的識別準(zhǔn)確率,結(jié)果如圖5所示.
測試結(jié)果表明,在數(shù)字調(diào)制信號方式識別的分類器選擇中,基于ILST-KSVC算法的分類器無論在分類識別率還是在訓(xùn)練所需時間上性能明顯優(yōu)于基于PNN算法與ISVM算法分類器.
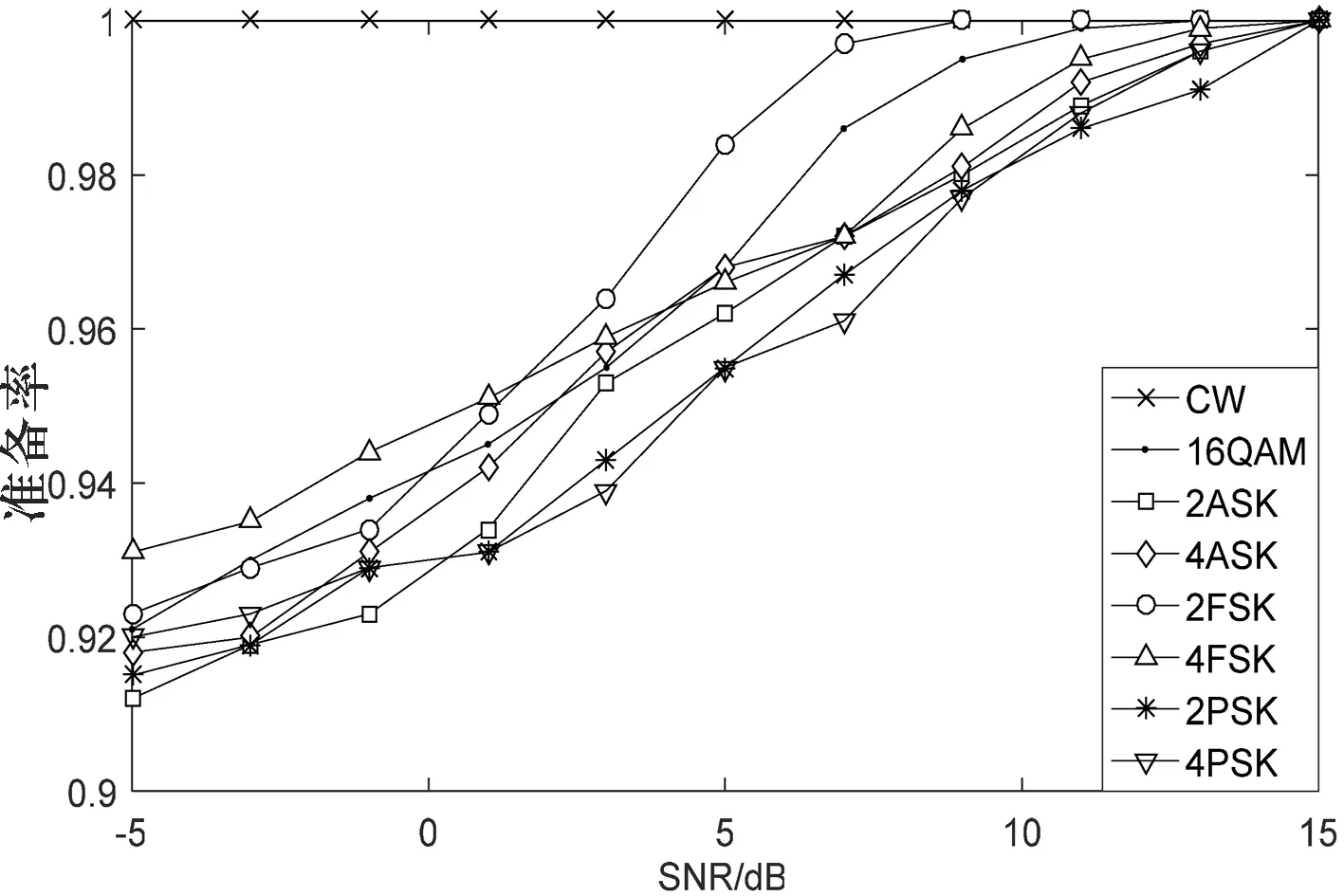
圖5基于ILST-KSVC分類器在不同信噪比下對多種調(diào)制方式的識別率
4 結(jié) 論
數(shù)字通信信號調(diào)制類型識別的難點在于信號經(jīng)過無線信道的傳輸后,信噪比變化范圍較大,這樣就使得同類信號的不同信噪比樣本提取的特征可能產(chǎn)生嚴(yán)重的畸變,即特征對信噪比變化很敏感.本研究通過分形理論,提出了一種對通信信號提取特征的有效方法.所提取的分形特征包含了區(qū)別不同調(diào)制類型所需的幅度、頻率和相位等主要信息,具有較好的抗干擾特性.本研究使用ILST-KSVC作為分類器,與使用PNN及SVM分類器的識別方法相比,能夠在低信噪比的條件下較好地完成不同數(shù)字信號調(diào)制方式的識別.

