基于整體最小二乘的空間直線擬合算法

崔立魯，楊 蓉，錢江宇，張惠妹，陳科潔

(1.成都大學 建筑與土木工程學院，四川 成都 610106； 2.武漢大學 測繪學院，湖北 武漢 430079)

0 引 言

關于利用測量數據如何對物體進行擬合的研究已成為工業測量系統發展的難題，其中常遇到的就是三維空間直線擬合問題[1].通常二維平面直線擬合可以直接利用最小二乘方法(Least squares,LS)和整體最小二乘方法(Total least squares,TLS)進行參數計算，但對于三維空間直線擬合由于其方程并不是一個簡單的線性關系，因此無法直接采用LS方法和TLS方法[2]，而需要對該方程進行一定的轉換.目前，常用的空間直線擬合方法有LS方法、牛頓—梯度最優化算法、無迭代算法、特征分解和選權迭代算法和結構總體最小二乘擬合等[3-7].本研究通過一定方式將空間直線方程轉變為TLS方法中的系數矩陣含有誤差(Error-in variable,EIV)模型，從而可以直接利用TLS方法進行參數擬合，且在計算過程中充分考慮了X、Y和Z坐標分量的測量誤差，最后利用工程測量中的大型構件的實際測量數據對上述方法進行參數擬合處理，并與其他幾種方法的結果進行了比較.

1 擬合算法

1.1 模型轉換

假設空間上的一條直線經過點P0(x0,y0,z0)，其方向向量為(D，E，F),則其空間直線標準方程為，

(1)

可改寫為，

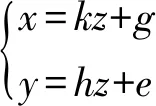
(2)

式中，k=A/C，g=x0-A/Cz0，h=B/C，e=y0-B/Cz0.

將式(2)寫成矩陣形式，即，

(3)

(4)

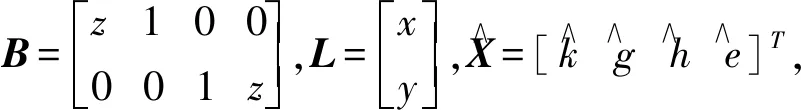
即為間接平差模型的形式.

1.2 LS方法

對式(2)的方程組進行改寫，其改正值如下，

(5)

當Vx和Vy取最小時，k、g、h與e即為方程的系數.因此，對式(5)中2個方程式分別求偏導數，其值等于0.經整理可得，

(6)

(7)

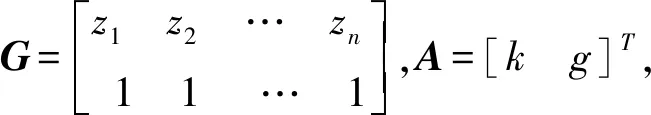
X=[x1…xn]T，B=[he]T，

Y=[y1…y2]T，

則改寫式(6)和式(7)成矩陣形式為，

(8)

對式(8)求解得到矩陣A、B的值，即為k、g、h與e的值.

1.3 TLS方法

1.3.1 基本思路.

TLS方法不僅考慮了觀測值的誤差，而且還顧及了系數矩陣的誤差，因此在理論上比LS方法更加嚴謹，其參數估值是最優的.建立顧及系數矩陣和觀測值誤差的EIV模型，即，

(9)

目前，針對EIV模型的求解，主要有SVD法、QR法和迭代法[10-11].其中，SVD法是認為系數矩陣B中的所有元素都是帶有誤差的，但是只有元素z才具有誤差，其他元素都是0或者1，因此從理論上來說沒有考慮完整而不夠嚴密.而迭代法計算簡單，又適用于編程計算，因此本研究采用迭代法來求解空間直線參數擬合中的EIV模型[12].

1.3.2 TLS的迭代法求解.

本研究提出的方法在式(6)的基礎上引入了平差準則，

(10)

將式(6)代入上式并對系數矩陣B和參數向量X中的各個元素求導，得到迭代法的方程式為，

(11)

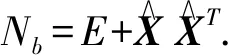
迭代法的計算流程如圖1所示.

2 擬合精度評定

衡量空間直線擬合精度的指標主要是直線度和點到直線的距離和.直線度是指實際直線與理論直線之間的變動量，即點到直線的距離最大差值，是最基本也是比較重要的評價指標.

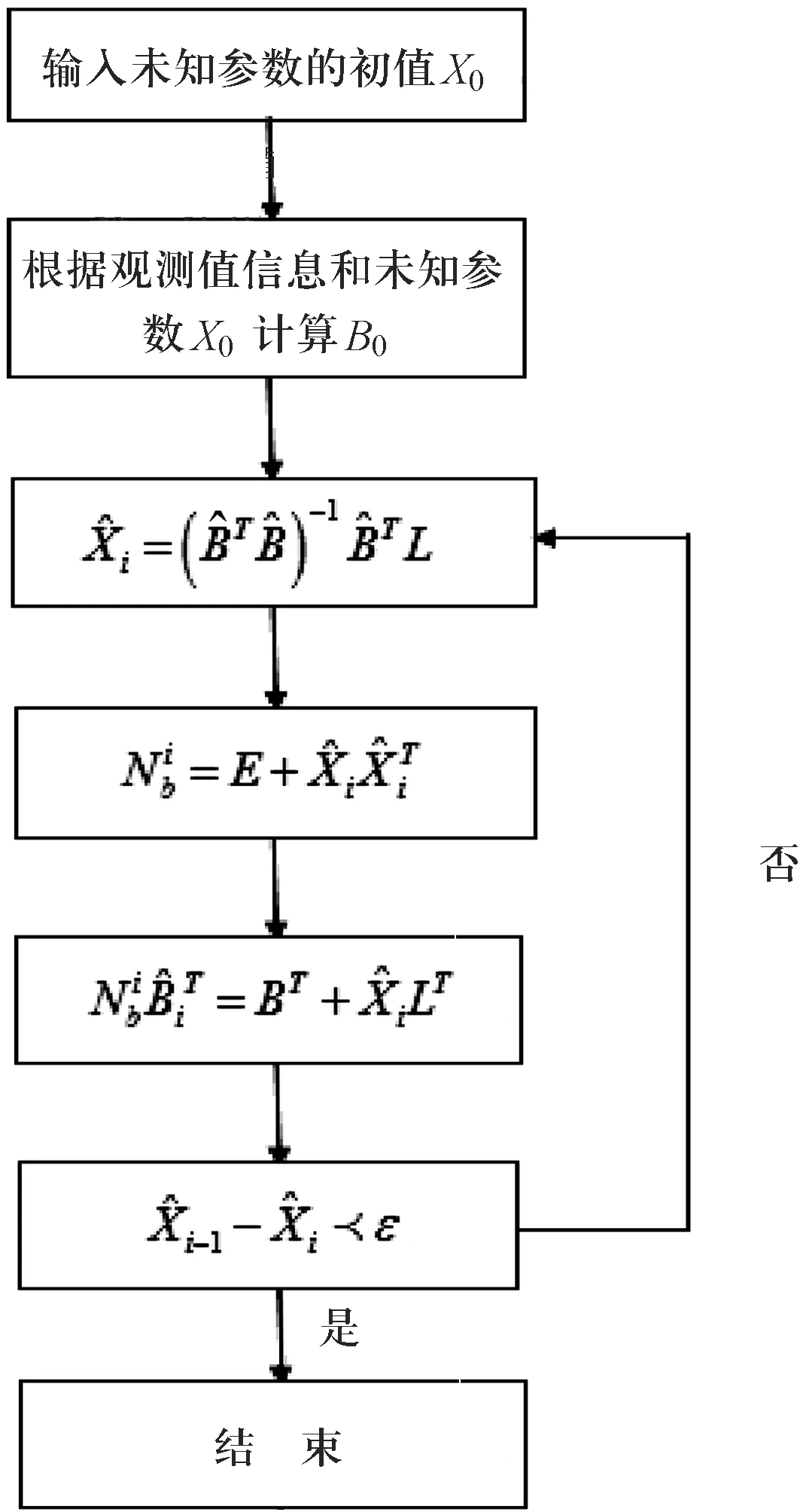
圖1迭代法流程圖

(12)

(13)

式中，(x0,y0,z0)是所有空間直線擬合點(xi,yi,zi)的平均值；(α，β，γ)為空間直線的方向向量，即式(1)中的(D，E，F).

3 算例分析

為了驗證本研究所提出的算法的正確性，采用工業測量中大型構件的測量數據進行計算，共計10個點，實際測量數據如表1所示[1].

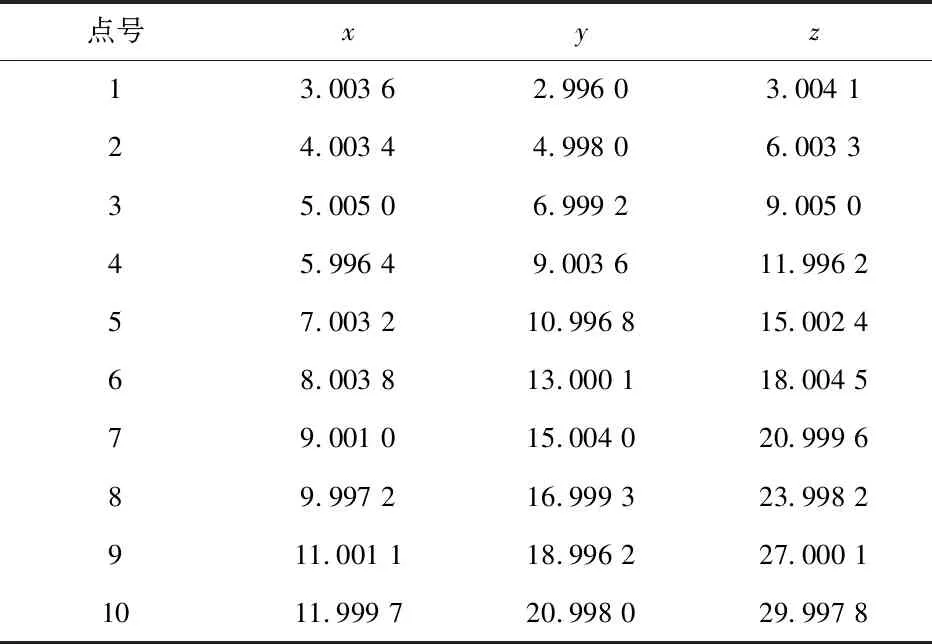
表1 空間直線實測數據

根據TLS方法和LS方法的基本原理，分別利用此2種方法對上述實測數據進行處理，得到計算結果如表2所示.

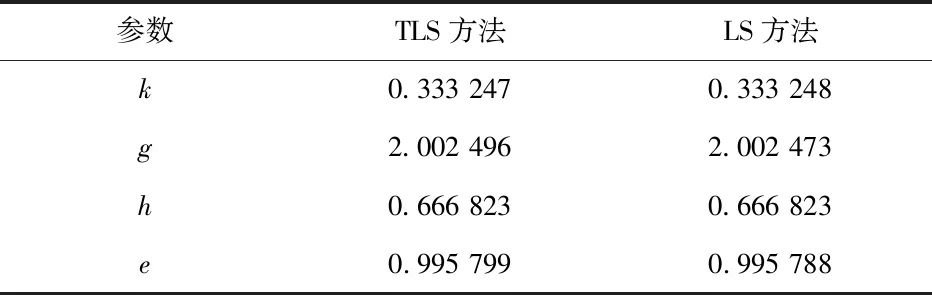
表2 空間直線參數擬合結果

由表2可知，TLS方法和LS方法擬合得到的4個參數基本一致，其中第3個參數完全一樣.將上述結果代入式(2)可得到關于4個參數的方程組分別為，

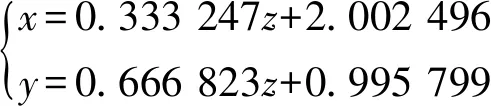
(14)

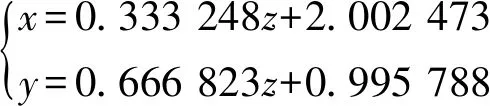
(15)

由于空間直線標準方程式的表達不是惟一的，所以同一組數據得到的參數形式是多樣的.根據式(1)和式(2)得到相應的空間直線標準方程式為，

(16)

(17)

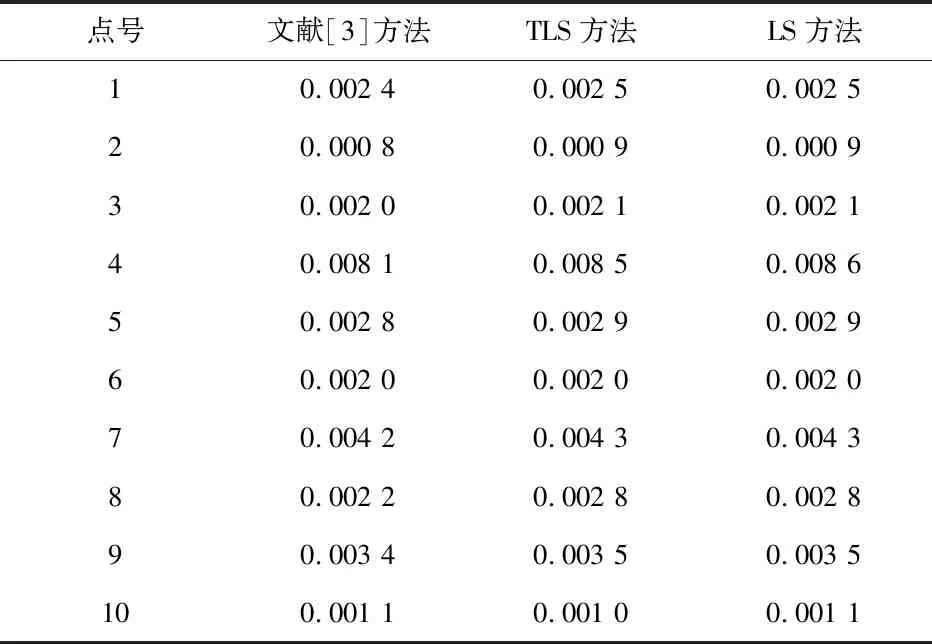
表3 2種方法計算結果的Δi統計

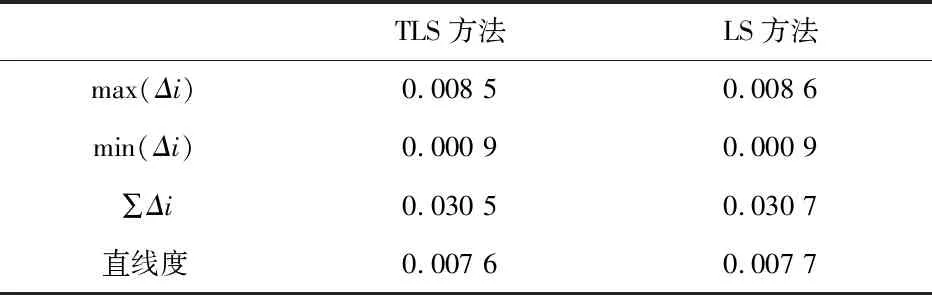
表4 2種方法的直線度比較

表3將文獻[3]方法、TLS方法和LS方法計算結果中每個點的點到直線距離誤差進行了比較.從表3可知，文獻[3]方法和本研究提出的TLS方法計算結果基本一致，這是因為本研究采用的是文獻[3]中的方法.因此，表3的計算結果從側面驗證了本研究編程計算結果的正確性，同時也證明了TLS方法精度高于LS方法.而表4的結果表明TLS方法的各項精度指標均優于LS方法，與表3結果得到的結論完全一致.

表5將文獻[1]、[3]、[5]和[7]的結果和本研究的計算結果進行了比較.從表5可知，本研究的結果精度高于文獻[1]，與文獻[5]和[7]基本一致，略低于文獻[3]，同時，本研究方法計算出來的方向向量和此4個文獻里計算得到的方向向量都非常接近(1∶2∶3).因此，表5的比較結果也充分證明了本文算法的正確性、可行性和有效性.

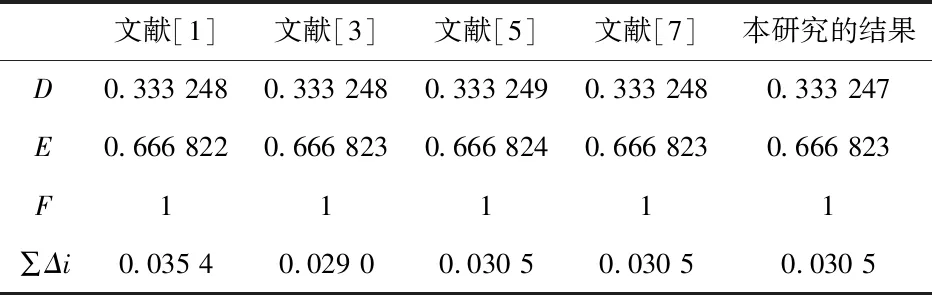
表5 各種方法計算結果的比較

4 結 語

鑒于TLS方法和LS方法不能直接應用于空間直線擬合計算，因此，本研究采用參數變換的方式將三維問題轉化為二維問題，構建出TLS方法中的EIV模型，并利用迭代法對EIV模型的結果進行求解[13-14]，然后分別利用TLS方法和LS方法對工業測量中的大型構件的實際測量數據進行參數擬合處理，并對2種方法的計算結果進行比較，以及本研究方法的結果與文獻中的結果進行詳細對比，充分驗證了本研究所提方法的正確性、可行性和有效性.