基于神經網絡自適應算法的機械手控制器的設計與仿真

李 斌 馬小瑞

（1.甘肅省工業和信息化廳信息中心，甘肅 蘭州 730000；2.甘肅省知識產權事務中心，甘肅 蘭州 730000）

0 引言

隨著機械、自動控制、計算機、人工智能和傳感器等技術的飛速發展，機器人已進入人們的現實生活。目前，工業機器人已成為現代制造系統中不可或缺的一種自動化裝備，被廣泛地應用在汽車、飛機、電子產品等行業的制造中，機器人不僅被應用在軍事、航天等尖端領域，而且正逐步走向社會、家庭領域，服務機器人已經進入人們的生活中。機器人技術已成為衡量一個國家綜合技術水平的標志之一。該文以雙臂機械手為例，首先確定機械手的動力學模型，根據已確定的被控對象進行控制方法的選擇和控制器的設計。由于機器人是高度非線性的不確定模型，因此采用李亞普諾夫穩定性理論進行穩定性分析和控制器設計。建立Lyapunov函數V，根據已經提出的控制器結合被控對象模型證明V＞0，V˙≤0，充分說明控制系統是全部或者局部漸進穩定的；最后，利用S-函數，在MATLAB的Simulink中設計控制系統主程序框圖，并且調用S-函數進行系統仿真或者利用純M文件編寫控制器和被控對象的命令函數。針對不同的控制方法構建主程序，并結合輸出圖形進行穩定性分析和控制性能比較。確定一個相同的雙臂機械手作為被控對象，利用不同的控制方法進行仿真比較，通過仿真結果比較得出各種控制方法的利弊。

1 機器人PID控制

1.1 S-函數與方程

S-函數模塊是整個Simulink動態系統的核心。Simulink在每個仿真階段都會對S-Function進行調用，不同的flag值調用不同的功能子函數，參數flag與S-函數回調函數的關系見表1。

1.2 機器人動力學模型及其結構特性

一個N關節機器人，其動態性能可由二階非線性微分方程描述：

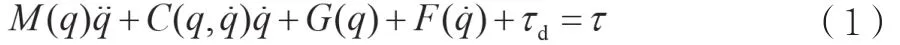
公式（1）中，q∈Rn*n為關節角位移量；M（q）∈Rn*n為機器人的慣性矩陣；∈Rn表示離心力和哥氏力；G（q）∈Rn是重力項；∈Rn表示摩擦力矩；τ∈Rn為控制力矩；τd∈Rn為外加擾動。

1.3 雙臂機械手的運動方程

當忽略重力和外力干擾時，采用獨立的PD控制，能滿足機器人定點控制的要求。

設雙臂機械手方程為：

2 機器人神經網絡自適應控制

主要對RBF網絡的基本原理、高斯基函數、網絡參數對逼近效果的影響以及基于RBF網絡逼近的Simulink連續系統仿真和M語言離散數字化仿真方法。

2.1 RBF網絡

2.1.1 RBF網絡結構

在RBF網絡結構中，X=[x1，x2，…xn]T為網絡的輸入向量。設RBF網絡的徑向基向量H=[h1，h2，…hm]T，其中hj為高斯基函數：

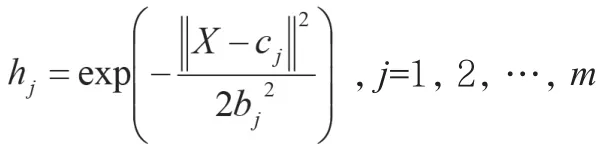
表1 參數flag與S-函數回調函數的關系

其中，網絡第 j個節點的中心矢量為cj=[cj1，…，cjn]。

設網絡的基寬向量為：

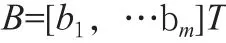
其中，bj為節點j的基寬度參數，且為大于零的數。網絡的權向量為：

RBF網絡的輸出為：

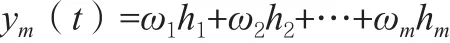
因此，任意連續函數都能利用RBF網絡來逼近。

2.1.2 RBF網絡逼近模型不確定部分

RBF網絡算法為：

其中，x 為網絡的輸入信號；φ=[φ1，φ2，…，φn]為高斯基函數的輸出；θ為神經網絡權值。

假設：

其中，θ*為n×n階矩陣，表示對f（x）最佳辨識的神經網絡權值。

2.2 基于模型不確定補償的RBF網絡機器人自適應控制

2.2.1 基于不確定補償的機器人建模

在實際中，對公式（2）所示對象很難建立具體模型，只能建立理想的名義模型。分別用D0（q），，G0（q）來表示機器人的名義模型。

根據模型精確建模時設計的控制律，針對名義模型，控制律設計為：

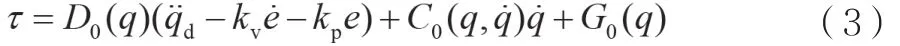
將控制律公式（3）帶入公式（2）中，得：

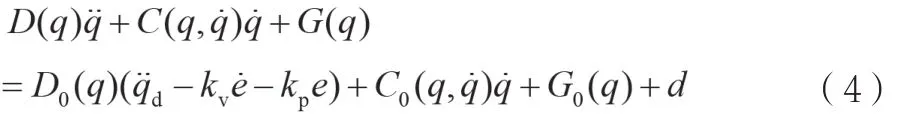
取ΔD=D-D，ΔC=C-C，ΔG=G-G則：

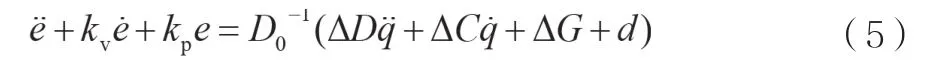
由公式（5）可知，由于模型建模不精確會導致控制性能的下降。因此，需要對模型不精確的部分進行辨識。

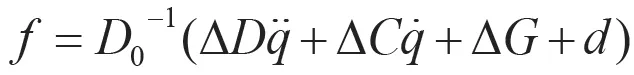
則得到在控制律公式（5）下的誤差方程為：

其中

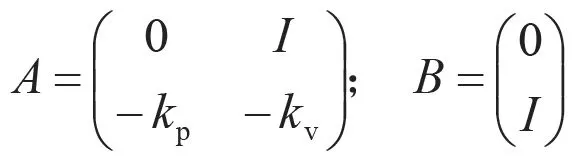
假設模型不確定項f已知，則修正的控制律為：

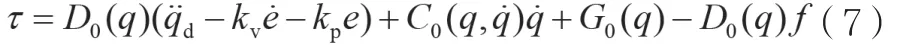
將控制律公式（7）帶入公式（2）中，得到穩定的閉環系統：

2.2.2 控制器的設計

控制器設計為：

其中，

取Lyapunov函數為：

可以采用2種自適應律設計方法。

2.2.2.1 自適應律之一

取自適應律為：

則

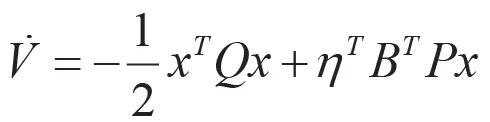
2.2.2.2 自適應律之二

取自適應律為：

則

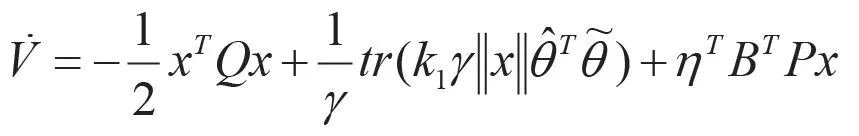
這種方法可以保證權值的有界性。

2.2.3 仿真實例

以雙力臂機械手控制為例進行控制器的仿真和結果比較。

對于雙關節機器人系統(忽略摩擦力)，其動力學模型為：

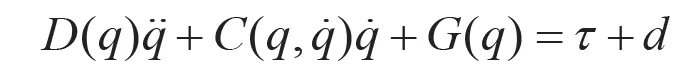
其中，

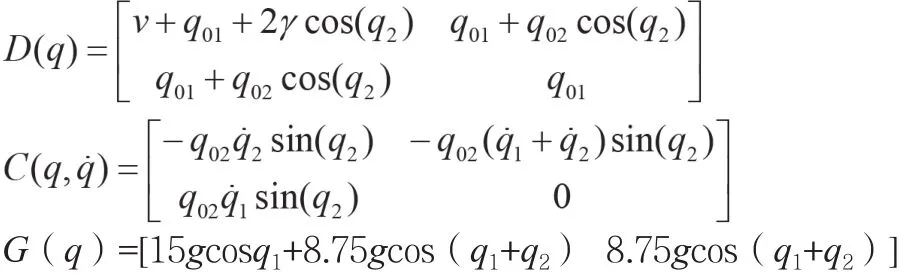
其中，v=13.33；q01=8.98；q02=8.75；g=9.8。

擾動誤差、位置指令和系統的初始狀態分別為：

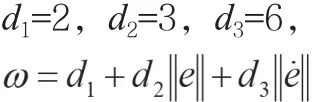
位置指令為：

控制參數取：

運行Simulink仿真主程序圖如圖1所示。

仿真結果如圖2所示。

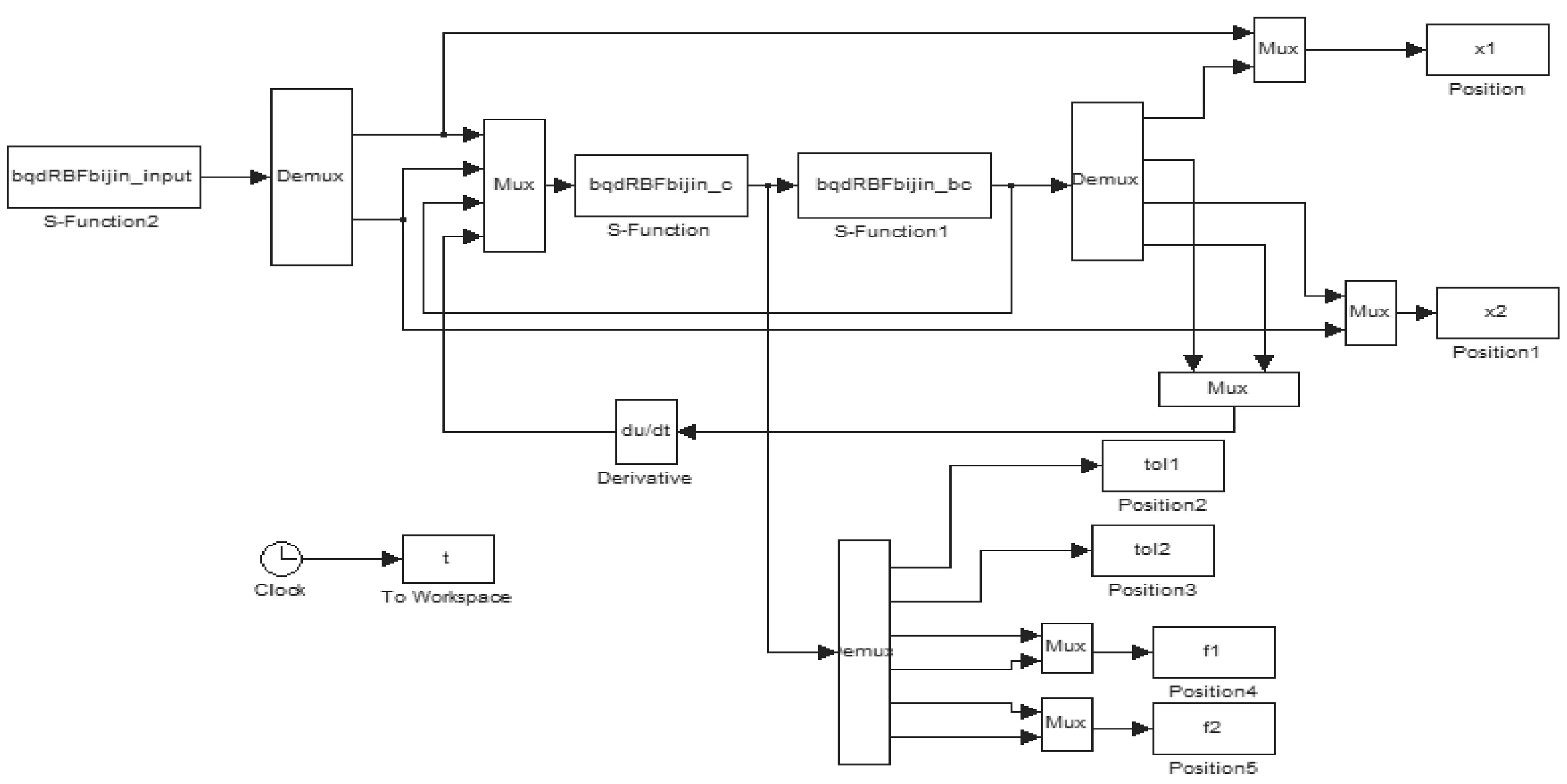
圖1 基于模型不確定補償的RBF網絡機器人自適應控制主程序圖

由仿真結果可知，采用此控制律可以保證權值的有界性，解決神經網絡權值的UUB（Unknown Upper Bound）問題，同時對機器人的不確定部分進行了補償。通過改變一些控制參數的特征值大小，象Q的特征值越大，P的特征值越小，并且減小神經網絡建模誤差η的上界，就可以使x的收斂半徑變小，從而達到改善跟蹤效果的目的。

2.3 基于模型分塊逼近的機器人RBF網絡自適應控制

2.3.1 基于分塊逼近的機器人建模

其中，ED、EC和EG分別為神經網絡對D（q）、和G（q）的建模誤差。

2.3.2 控制律的設計

定義

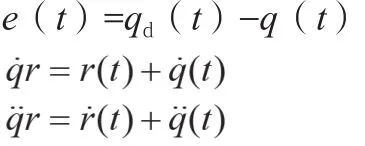
其中，qd（t）為理想的位置指令；q（t）為實際的位置。

定義

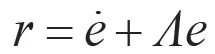
則

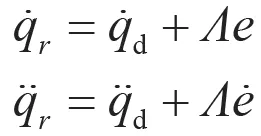
其中，Λ＞0。

設對神經網絡建模項DSNN（q）、CDNN、GSNN（q）的估計值為：

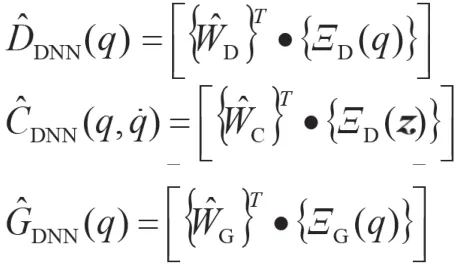
控制律設計為：

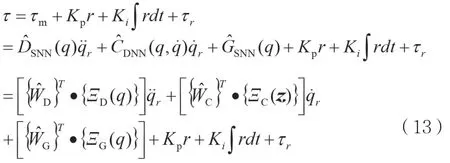
其中，Kp＞0 ；Ki＞0。

自適應律設計為：

2.3.3 穩定性分析

取Lyapunov函數為：

圖2 基于模型不確定補償的RBF網絡機器人自適應控制

其中，ΓDk，ΓCk，ΓGk為對稱正定矩陣；，

則

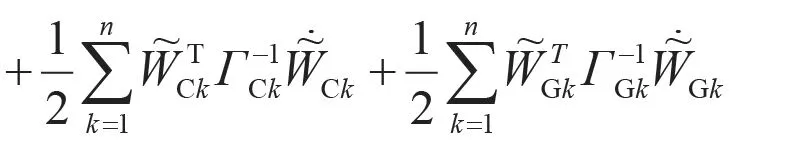
經分析得到：

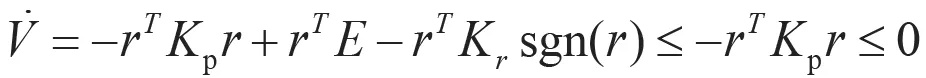
2.3.4 仿真實例

以雙力臂機械手控制為例進行仿真和比較。選二關節機器人系統（不考慮摩擦力和干擾），其動力學模型為：

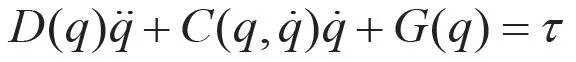
其中，

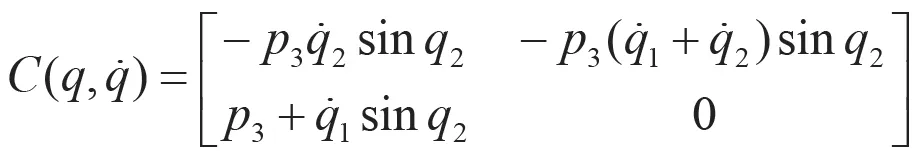
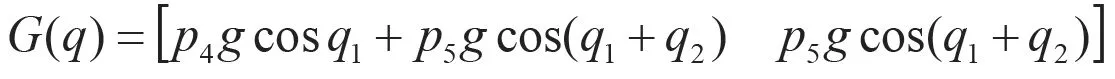
取控制器參數為

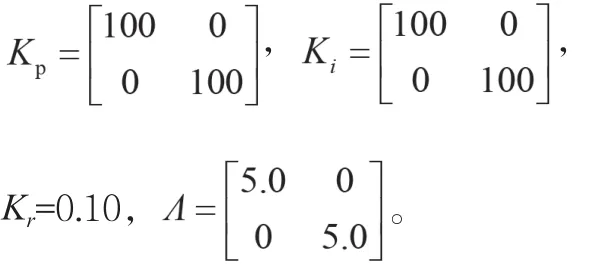
仿真結果如圖4所示。

由仿真結果可知：各關節的位置均能跟蹤系統所給的理想軌跡。控制律能夠在一定的范圍內有規律的變化。可以實現對實際模型中未知部分D（q）、和G（q）的高效逼近。因此，基于模型分塊逼近的RBF神經網絡自適應控制性能較好。

3 基于RBF網絡的雙機械力臂自適應數字控制

選擇雙力臂機械手作為被控對象。在不考慮摩擦力和外界干擾的情況下，其動力學模型為：

仿真中采用了MATLAB函數“ode45”積分求解。采樣時間取ts=0.001，將控制律公式（13）和自適應律公式（14）（15）（16）離散化，取，。取控制律參數為

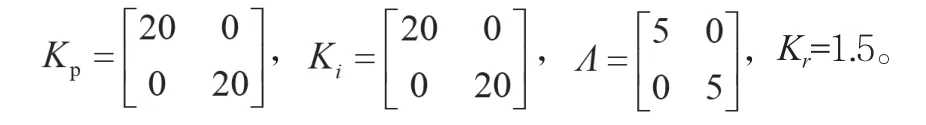
位置指令為qd1=qd2=0.5si（n2πk·ts）。自適應中，神經網絡權值調節矩陣ΓDk，ΓCk和ΓGk中的元素值分別取5、10、10。RBF網絡的隱含層節點數取5，用于逼近的，，的高斯基參數見控制器子程序。仿真結果分別如圖5和圖6所示。

由仿真結果可知：該例中RBF網絡隱含層節點采用了node=5，從t=1.25之后各關節的位置基本可以跟蹤理想軌跡；改變隱含層節點個數，當node=2時，關節1和關節2均不能完全跟蹤理想軌跡；當node=3時，從t=1.5之后各關節的位置可以完全跟蹤理想軌跡；當node=10時，從t=0.75之后各關節的位置可以完全跟蹤理想軌跡。因此，基于RBF網絡的雙機械力臂自適應數字控制可以通過增加神經網絡隱含層節點的個數，達到更迅速更逼近的控制效果。同樣，隱含層節點的個數太多會增加網絡運算的復雜性。

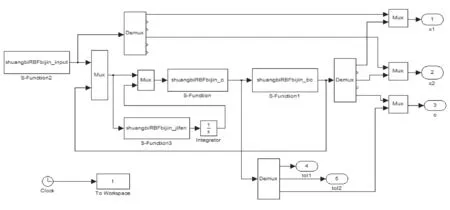
圖3 基于模型分塊逼近的機器人RBF網絡自適應控制

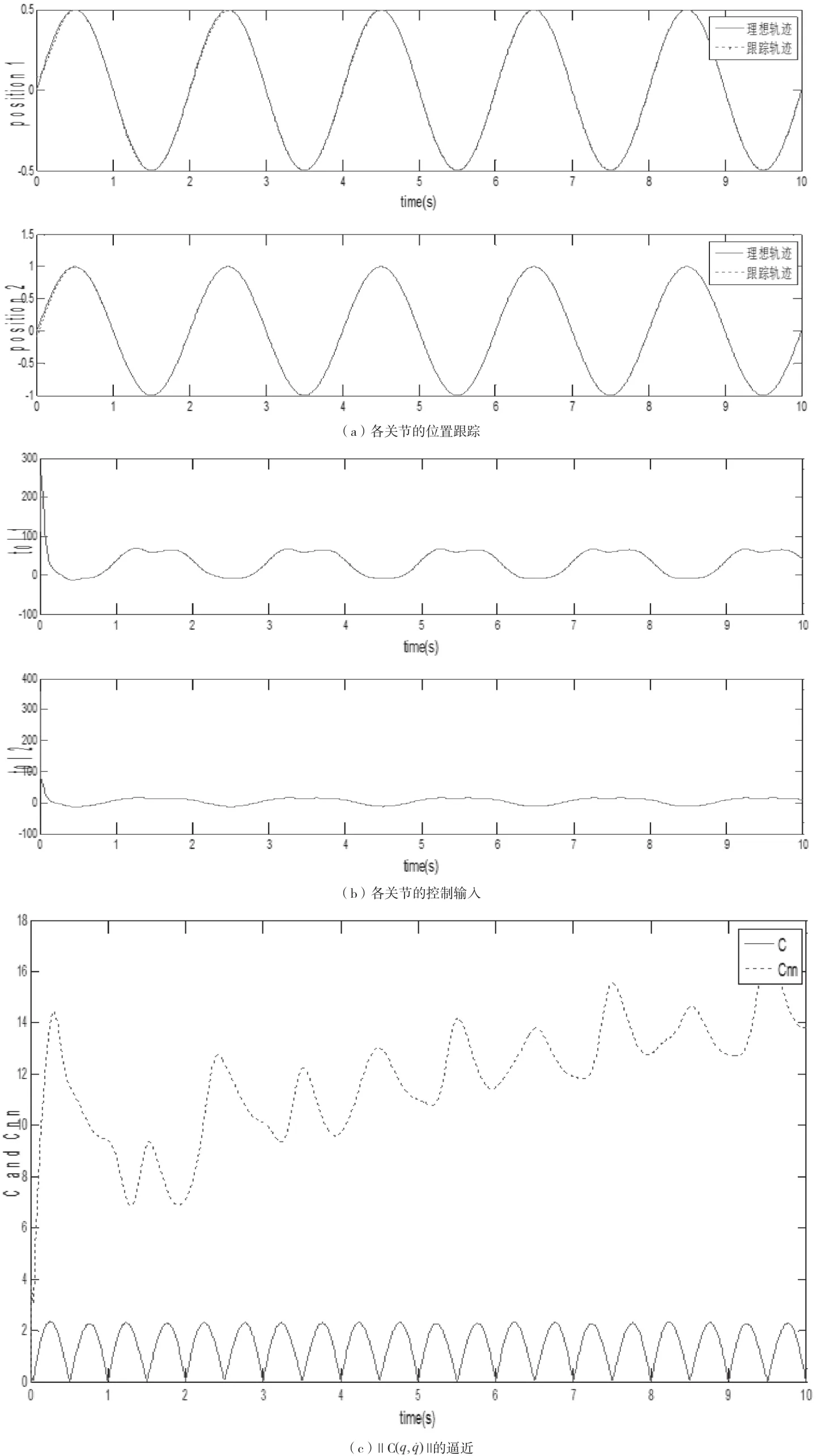
圖4 基于模型分塊逼近的機器人RBF網絡自適應控制

4 結論

該文在分析機器人雙臂機械手控制的基礎上，提出了機器人雙臂機械手的神經網絡控制算法。在被控對象為非線性模型的情況下，利用RBF網絡自適應方法設計控制器。通過編寫控制器和被控對象的S-函數或M文件，運用仿真知識并對運行結果進行比較和穩定性分析。

通過Lyapunov穩定性理論得到的控制器可使系統要么達到局部漸進穩定，要么達到全局漸進穩定。采用RBF神經網絡控制可以實現對機器人動力學方程中未知部分的在線精確逼近，從而可通過在線建模和前饋補償的方式，實現機器人的高精度跟蹤，其結果與被控對象已知時基本一致，控制性能良好。雙臂機械手是在單臂機械手的基礎上又增加了一維標量，它的控制方法與單臂類似。以此類推，以后多關節機械手的控制器設計，也可以認為是多個單臂的綜合，只是設計問題會隨著關節數的增多而變得更復雜、更困難。該文提出的RBF神經網絡算法對機器人雙臂控制的仿真結果可以看出，該算法可以提升各關節的控制性能，使其更好地完成控制需求。

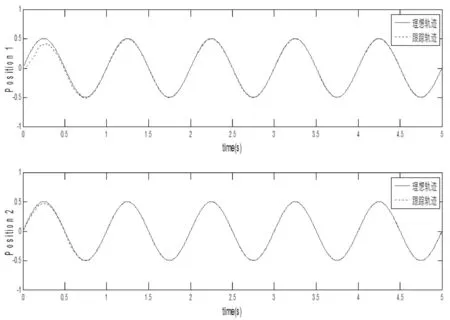
圖5 各關節的位置跟蹤

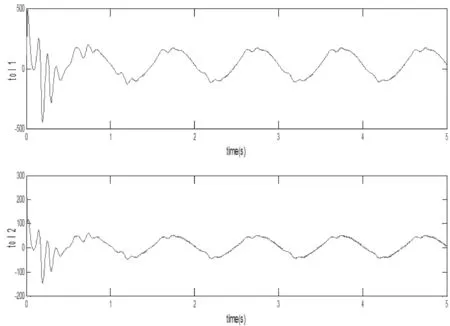
圖6 各關節的控制輸入