基于時效規則的數據修復方法?

2019-04-18 05:06:46段旭良申云成董祥千

軟件學報 2019年3期

段旭良,郭兵,沈艷,申云成,董祥千,張洪

1(四川大學計算機學院,四川成都 610065)

2(成都信息工程大學控制工程學院,四川成都 610054)

3(四川農業大學信息工程學院,四川雅安 625014)

時效性是數據的重要屬性,在數據挖掘、數據分析、數據增值應用中,準確的數據時效決定著諸如時間序列分析、關聯、推薦等一系列算法的效果.相關學者采用直接觀測、社會調查、理論推導等方式對數據質量問題展開研究,并分析得出對數據可用性影響較大的性質有:精確性、完整性、一致性、時效性和實體同一性[1].2002年有專家報告指出:在商業數據領域,由于客戶信息的變化,每月有2%的商業數據陳舊過時[2,3].大量時效不精確的數據充斥在數據集中,如果不能識別哪些是最新的,數據查詢可能會返回錯誤結果,數據分析可能產生相悖的結論,隨之而來的是數據質量下降、數據價值降低.大數據時代,人們的各類數據非集中化地分布于各類平臺和系統中,形成數據孤島,數據時效不精確、數據過時帶來的問題愈加嚴重.

不確定數據的產生原因很多,但總體可以歸結為客觀條件限制和人為故意兩大因素:客觀條件限制包括環境影響、采集設備精度限制、傳輸錯誤和意外事故導致的數據缺失或不精確;人為故意則是為了滿足特定需求,如隱私保護等,對原始數據進行模糊化處理.針對數據修復工作的相關研究主要集中在數據不一致、不精確、不完整等問題上,研究者和工程技術人員提出了一系列針對這些問題的數據修復方法.從20世紀80年代開始,針對不確定性數據的概率數據庫(probabilistic database)相關研究一直在進行,這類研究工作將不確定性引入到關系數據模型中去,研究領域涵蓋了模型定義、預處理與集成、存儲與索引、查詢與分析等基礎和應用研究的各個方面[4,5].針對不完全、不確定數據查詢的研究較早地涉及到時效缺失或者時效不精確等問題,包括時態數據庫模型構建、相關查詢語言定義與分析等[6,7].

大數據和人工智能時代,個人大數據蘊藏著不可估量的社會和經濟價值,個人數據銀行模式是一種有效整理整合個人數據、提高個人數據質量和價值、增強個人數據可控性和可用性、有效保護個人數據隱私的新模式[8].在數據匯聚過程中,由于個人數據的分散度高、可管理性差,面臨著更多的冗余和數據不一致問題,數據質量也難以保證,很大程度上影響著數據銀行模式的健康發展.同時,個人數據又是一種典型的動態數據,反映個人屬性、狀態的各項數據是不斷動態變化的,這個特性也是個人數據清洗過程中面臨的最大挑戰.在數據銀行模式下,為了保證數據質量、提高數據價值,需要匯聚來源眾多的數據,其時間屬性往往是不精確的[9].對數據某些屬性來說,不同時間對應不同值或狀態,如一個人的學歷變化、婚姻狀況變化等,如果時間戳不完整或不精確,無法判定記錄先后關系,會給數據增值應用帶來極大的困難.

當前,國內外針對數據時效性修復的相關文獻總體較少,專門應用到數據時效恢復的方法不多,大致可以分為兩種:基于語義規則的方法和基于統計的方法.基于語義規則的方法根據領域專家知識或函數依賴、條件依賴、時效依賴,發現數據錯誤進行修復[10,11];基于統計的方法通過分析數據規律,如可能世界模型及概率數據庫等相關方法,目的是尋求最大正確可能的修復策略[5,12].

雖然數據時效性問題面臨的形勢非常嚴峻,但并不是毫無希望.2011年前后,Fan等人提出了基于數據語義信息推斷數據缺失值的數據時效性修復問題,在同一個實體具有多個元組的假設下,對數據時效性模型(a model for data currency)、數據時效性推理(reasoning about data currency)、時效性復制(currency preserving copy functions)等領域問題進行了深入研究,對相關概念進行了形式化的描述及定義,將這一領域的基礎理論研究向前推進了一大步[13,14].在此工作的基礎上,又有一系列卓有成效的研究在理論和實踐上推動了數據時效性修復相關研究進展.文獻[10]基于數據時效和數據一致性解決同一實體不同元組屬性不一致的情況,提出采用數據的局部時效順序表示數據的可用時間信息,在數據中提取時效約束條件表示數據時效關系,根據常量條件函數依賴確定數據的最新值.文獻[15]研究了包含冗余記錄的集合在給定時效約束下的時效性判定問題,提出了時效性判定問題的求解算法;文獻[16]研究了規則和統計相結合的過時數據修復方法,既能夠以傳統規則的方式表達領域知識,又可以使用其特有的分布表來描述數據隨時間變化的統計信息;文獻[17]提出了一種結合質量規則和統計技術的提高數據時效性的修復方法;文獻[18,19]提出在動態數據集上通過構建實體查詢 B-樹和實體存儲靜態/動態鏈接列表提高數據時效性確定效率和加速數據時效更新,提高了在大數據集上時效處理效率.

數據時間戳的恢復是研究的一個難點,如果數據時間戳缺失,是很難進行精確修復的;而根據一些規則,還原數據先后關系,確定缺失時間戳的區間范圍,是一種可行、有效的策略.文獻[20]提出了采用時序約束修復數據時間戳的方法,采用最小化修改原則使事件滿足時序約束條件,一方面可以恢復缺失時間戳事件的所在時間范圍;另一方面,也可以用于異常發現,對違背時間約束的事件進行檢測和修復.實際上,在大多數數據分析和應用中,對數據先后關系的依賴相對于精確的時間顯得更為重要,如廣泛應用的時間序列、關聯、推薦等一系列算法,基本都是以數據順序作為基礎實現相關功能.因此,對缺失時間戳數據的時間順序進行修復既可以滿足大多數分析應用對順序的要求,又可以確定記錄的新舊滿足時效性查詢需求,有利于數據質量和數據價值的提升.

數據時效性是決定數據質量的關鍵因素之一,本文主要研究時間戳缺失或者不精確的情況下,同一實體不同屬性值的時序修復問題,在之前學者研究的基礎上,重點針對“時序”即記錄時間順序開展研究工作.第 1節進一步明確時效規則的形式化定義,分類和定義值類型時效規則、狀態類型時效規則,并對時效規則的支持度進行了定義.第2節提出狀態類型時效規則提取和數據修復算法,并以實際算例展示算法過程和原理.第3節為實驗結果與分析,在真實的數據集上驗證規則和算法的效率和有效性,分析與討論影響時效修復算法效率和正確率的相關因素.最后總結全文,并對未來值得關注的研究方向進行初步探討.

1 時效規則概念和定義

本文定義的時效規則是指同一實體在不同時間階段的數據記錄在某些屬性上隨時間推移表現出的一些規律性特征.令關系數據庫模式R=(EID,A1,…,An),其中,EID為實體標識符,具有相同EID的不同的元組對應同一實體(entity),EID可以由實體識別技術生成[21,22];Ai為第i個屬性,其值域為dom(Ai).

定義1(屬性的時效規則).對于關系R上同一數據實體的元組,某些屬性依元組的時間順序表現出遞增、遞減或服從特定的狀態轉換序列,我們稱該屬性滿足時效規則.若屬性Ai滿足時效規則,參照Fan等人關于數據時序的定義,將其表示為

即:對于關系R中同一實體的元組t1,t2,如果t2比t1新,則元組t2的Ai屬性比t1元組的新.

在此,我們假定數據是一致的,不違背函數依賴和條件依賴關系,即:不存在t1中的某一屬性Ai比t2中的新,則以下關系依然成立:

即:對于同一實體的兩個元組t1,t2,如果Ai滿足時效規則,且t2的Ai屬性值比t1新,則元組t2比t1新.

例如,年齡隨時間遞增,一個人的學位狀態為學士、碩士、博士,婚姻狀態為未婚、已婚、離婚等,則年齡、學歷、婚姻狀況等均滿足時效規則.反過來,如果記錄一個人的兩條數據中學歷狀態分別為博士、碩士,則學歷為博士的數據更加的新一些.

定義2(值類型時效規則).關系R上對于隸屬于同一實體的兩個元組t1,t2,如果某一數值屬性Ai滿足:

我們稱Ai為值類型時效規則.反過來也成立:

例如,人的年齡、一般情況下的薪酬都是隨時間遞增的.

定義3(狀態型時效規則).關系R上,屬性Ai的所有不重復值作為有限狀態集合,表達屬性時效規則的狀態圖是一個有向圖G(V,E),其中,頂點集V表示屬性值(狀態)的有限集合,有向邊集E表示隨時間先后順序狀態遷移的方向.對于關系R上隸屬于同一實體的兩個元組t1,t2,其屬性Ai的值分別為v1,v2,且v1,v2為圖G的狀態結點,若t2比t1新,則在狀態圖G中,v1到v2可達且v2到v1不可達,稱v1→v2為一條狀態型時效規則,表示如下:

同理,在一致的數據集上:

如,學位狀態或學生不同學期選課狀態可用有向圖如圖1所示.

Fig.1 Directed graph of attribute state changing圖1 表示屬性狀態變化的有向圖

其中,如果兩個狀態之間無環,則這兩個狀態存在確定的時序關系,否則時序關系不確定;如在學位狀態中,“本科”“碩士”“博士”存在先后關系;選課狀態中,“C 語言”狀態在“計算機基礎”狀態之后,而僅依靠“C 語言”“數據結構”或“C語言”“離散數學”無法確定先后順序.一般地,考慮到數據記錄的缺失,從無環規則起點狀態到后續狀態節點形成的路徑依然是有時序關系的,如“學士”到“博士”、“計算機基礎”到“數據結構”、“計算機基礎”到“離散數學”等.

定義4(強時效規則).在一致的數據集上,如果所有實體上都滿足某屬性的一條時效規則,則稱為強時效規則.如,沒有某人的年齡會逐年遞減.所有人的年齡都是隨時間非遞減的,就是一條強時效規則.

定義5(弱狀態時效規則).在一致的數據集上,如果只有部分實體滿足某屬性的一條時效規則,則稱為弱狀態時效規則,用支持度來衡量該規則的強弱.實際上弱狀態時效規則用支持度對狀態型時效規則進行了擴充,若某條狀態時效規則的支持度為1,則它是一條強時效規則,否則即為弱時效規則.

定義6(狀態時效規則的支持度).在一致的數據集上,對于某屬性的一條狀態時效規則,滿足該規則實體數與滿足和違背該規則實體數之和的比值稱為該時效規則的支持度,表示如下:

其中,sr表示規則r的支持度,S(r)表示滿足規則r的實體集合,|S(r)|表示求集合中實體數量,V(r)表示違背該規則的實體集合,|V(r)|表示違背規則r的實體數量.

例如在選課狀態圖中,邊的權值表示數據集中滿足這條路徑規則的實體數量,對于學生的選課規則“C語言→數據結構”,圖2表示有99人先修“C語言”后修“數據結構”,有1人先修“數據結構”后修“C語言”,則“C語言→數據結構”這條規則的支持度為99/(99+1)×100%=99%.同理,“C語言→離散數學”這條規則的支持度為50%.

Fig.2 Calculation of rule support in a directed graph圖2 有向圖中規則支持度的計算

定義7(狀態時效規則的強度).規則的強度直觀上描述的是規則的重復次數越多,強度越高.需要說明的是:參見對支持度的定義,如果從某個狀態節點v1到v2有且僅有一條有向邊,但是v2到v1不可達,規則v1→v2的支持度依然為 100%,但這條規則可能是一個特殊的個例,重復性極低、代表性差,對數據時效修復價值不大.考慮到這種情況,引入了規則強度的概念,即規則的重復次數越多,強度越高.強度函數應根據數據實際特征進行定義.本文在實驗測試中使用了Logistic函數作為強度函數.

2 時效規則提取及數據修復

2.1 狀態時效規則提取

本文重點討論狀態類型時效規則識別.在一個數據集中,不同實體某些字段的狀態轉換是符合特定順序的.根據在數據集中提取的狀態時效規則,可實現對部分實體記錄的缺失時序進行修復.在某屬性的狀態類型時效規則提取過程中,首先按時間順序提取每個實體在該屬性上的狀態變化有向圖,然后對圖進行清理合并,計算圖中存在關聯關系狀態轉移的支持度.規則提取的結果可用有向圖G(V,E)結構表達,結點集V表示有限的狀態集合,有向邊集E表示一條邊連接的兩個結點的狀態轉移方向,有向邊的權值為兩個狀態轉移支持度大小.

下面用實例說明狀態類型時效規則提取方法和流程.

例1:狀態類型時效規則提取.

首先用示例說明狀態類型時效規則提取流程.設兩個學生A,B選課序列按時間順序排序后,分別為:

·A:計算機基礎→C語言→數據結構→數據庫;

·B:計算機基礎→數據結構→C語言→數據庫.

將課程作為狀態,通過以下操作即可完成狀態類型時效規則識別.

(1) 提取A的時效規則,分別為“計算機基礎→C語言”“計算機基礎→數據結構”“計算機基礎→數據庫”“C語言→數據結構”“C語言→數據庫”“數據結構→數據庫”;

(2) 提取B的時效規則,分別為“計算機基礎→數據結構”“計算機基礎→C語言”“計算機基礎→數據庫”“數據結構→C語言”“數據結構→數據庫”“C語言→數據庫”;

(3) 合并A,B規則,生成狀態屬性的有向圖,如圖3所示;

(4) 清理后狀態屬性有向圖如圖4所示,邊的權值表示滿足該時效規則的實體數;

(5) 計算規則支持度.根據定義6,計算所有規則的支持度.由圖4可知:除規則“數據結構→C語言”“C語言→數據結構”支持度為50%外,其他所有規則支持度為100%.不難推算,假設學生C的選課序列和A一致,則“C語言→數據結構”支持度為66.7%,“數據結構→C語言”支持度為33.3%,其他規則支持度依然為100%.

Fig.3 Directed graph of state attributes derived from data set圖3 從數據中提取的屬性狀態有向圖

Fig.4 Calculating the weight of edges in directed graph圖4 計算有向圖中邊的權值

需要說明的是:該算法支持動態增量數據集,當有新數據實體的記錄加入時,可在原來基礎上進行動態更新,不必在整個數據集上重新計算.由例1可見:當狀態數比較多、規則比較復雜時會形成非常復雜的狀態圖,使用鄰接矩陣表示會造成很大的存儲開銷.同時,查找路徑、遍歷圖代價也很高.考慮到每條時效規則實際上就是連接兩個狀態節點的一條邊,算法實現采用哈希表“鍵-值”(Hashtable,key-value)數據結構,以規則作為鍵,以滿足該規則的實體數量作為值,實現規則的高效添加和檢索.理論上,一個哈希表結構存儲的“鍵-值”對可以是無限多個,但是檢索的時間代價為常數復雜度O(1),回避了對復雜圖結構的高代價遍歷,可極大提升算法運行效率.狀態類型時效規則提取算法詳見算法1.

算法1.狀態類型時效規則提取算法.

輸入:已完成實體識別的、一致的、包含時序標簽的數據集R;E為實體集,e為某個實體,e∈E,一個實體e對應數據集中n條記錄;

輸出:哈希表表示的“規則-規則支持度”集合.

2.2 基于規則的時序修復

時間作為一個連續值,一旦缺失,幾乎沒有辦法被精確恢復.數據時效修復算法的目的是根據特定規則恢復同一實體記錄間的時間順序,根據時間順序判斷記錄的早晚和某些屬性值的新舊,滿足數據分析處理應用和查詢時效性需求.

例2和例3通過實例直觀地展示了基于狀態時效規則進行時序修復的原理和過程.

例2:數據時效修復實例.

下面用示例說明時效修復算法流程,我們已經通過例 1的學生A,B選課序列得到了全部規則及其支持度,見表1.

Table 1 Support of different rules in example 1表1 算例1中不同規則的支持度

假設已知學生C的選課序列:①計算機基礎→②C語言→③數據結構,①～③表示數據記錄時間索引,順序排列;一門課“數據庫”的時間屬性缺失,下面要做的是通過時效規則匹配還原“數據庫”這門課程在選課序列中的位置.

(1) 以“數據庫”為起始結點窮舉路徑,得到“數據庫→計算機基礎”“數據庫→C語言”“數據庫→數據結構”;

(2) 以“數據庫”為終止結點窮舉路徑,得到“計算機基礎→數據庫”“C語言→數據庫”“數據結構→數據庫”;

(3) 在“規則-支持度”哈希表中依次檢查滿足大于支持度(如要求支持度>60%)的步驟(1)中的規則是否存在:若存在,將規則后件時間索引添加到后繼時序列表中.檢查發現,“規則-支持度”哈希表中無步驟(1)中的規則,后繼時序列表為空;

(4) 在“規則-支持度”哈希表中依次檢查滿足大于支持度(如要求支持度>60%)的步驟(2)中的規則是否存在:若存在,將規則前件時間索引添加到前驅時序列表中.檢查發現:“計算機基礎→數據庫”“C 語言→數據庫”“數據結構→數據庫”均滿足支持度要求(100%>60%),規則“計算機基礎→數據庫”的前件“計算機基礎”時間索引為①,規則“C 語言→數據庫”前件“C語言”時間索引為②,規則“數據結構→數據庫”的前件“數據結構”時間索引為③,因此,前驅時序列表為{① ,②,③};

(5) 處理步驟(3)、步驟(4)生成的后繼前驅時序列表,確定當前狀態“數據庫”時序.此例中,后繼時序列表為空,可確定“數據庫”狀態結點出度0是圖的一個終點,前驅時序列表為{① ,②,③ } ,因此可確定“數據庫”時序索引為④,完成時效順序恢復:①計算機基礎→②C語言→③數據結構→④數據庫.

例3:假設已知學生C的選課序列:①計算機基礎→②C語言→③數據庫,①～③表示數據記錄時間索引,順序排列;一門課“數據結構”的時間屬性缺失,通過時效規則匹配還原“數據結構”這門課程在選課序列中的位置.

根據例 2的處理流程,可得“數據結構”的前驅時序列表為{①},后繼時序列表為{③},可確定“數據結構”時序索引為②,但其與“②C 語言”先后關系不確定.修復后,各狀態時序為:①計算機基礎→{②C 語言,②數據結構}→③數據庫.

但是如果假定“C語言→數據結構”支持度為66.7%,“數據結構→C語言”支持度為33.3%,其他規則不變,依然要求支持度>60%,則“數據結構”的前驅時序列表為{①,②},后繼時序列表為{③},可通過插值確定“數據結構”時序索引,如2.5,修復后各狀態時序為:①計算機基礎→②C語言→③數據結構→④數據庫.

算法2描述了對數據進行時效順序修復算法原理和流程,其返回結果為補充了時序標簽的記錄集.

算法2.數據時效修復算法.

輸入:哈希表表示的“規則-規則支持度”集合RuleSupportHash,完成實體識別的、一致的、包含時序標簽的數據集R,待修復的缺失數據標簽的記錄集R′;

輸出:補充了時序標簽的記錄集R″.

3 實驗結果與分析

3.1 實驗配置

實驗硬件環境為Intel i3 2130 3.4GHz CPU,6G內存,操作系統為Windows10,所有算法均采用C#實現.

測試數據集為某高校教務系統選課數據,無異常數據,數據記錄字段包括課程名、教學班編號、學號、學期等.必修課按培養方案一般安排在固定學期,具有較強的時序性,選修課則沒有明確限制.但該高校在處理學生選課過程中較為靈活,學生可以根據自己情況選修本專業或其他專業必修、選修,也可提前選修本專業必修課,如某學生可能在大一選修大四某門必修課,在大二選修大三某門必修課,因此時效規則面臨更多的不確定性,個別學生的隨意選課也可視作噪聲數據.根據實驗需求分兩部分.

(1) 數據集1為2014級8 626人的7個學期532 417條選課數據,平均每人60條選課記錄,覆蓋全校2 200多門課程,主要用于時效規則提取;

(2) 數據集2為2015級9 500人的5個學期472 962條選課數據,平均每人50條記錄,主要用于時效修復測試.

數據預處理:在數據集中,選課時間形如“2017-2018-1”的字符串,表示2017-2018學年第1學期,為方便處理,針對每一個實體的全部記錄,按選課學期升序排列,依次將選課學期處理為 1,2,3,…,7數值形式,“1”表示學生入校后第1學期,“2”表示學生入校后第2學期,依此類推.

算法針對每個學生每門課程選課學期的先后順序提取時效規則,并進行時效修復實驗.實驗中提到的相關術語解釋如下.

(1) 狀態:指狀態圖中的狀態結點.這里測試我們選取課程名作為狀態,相同的課程名表示相同的圖結點,不同的課程名表示不同的圖結點.采用的測試數據中,總計有2 200多門課程,意味著狀態圖中最多有2 200多個結點;

(2) 實體:測試中的實體即學號.測試數據集中,一個實體對應多條數據記錄,即:同一個學生有多條選課記錄,學號相同的記錄是同一個人的選課數據;

(3) 狀態類型的時效規則,下文敘述中簡稱規則.對于實驗數據集來說,規則可以解釋為選課的先后順序.

3.2 狀態時效規則提取算法參數及效率分析

實驗主要測試算法執行效率及影響算法效率的相關因素.時效規則生成需掃描數據集1中每個學生的7個學期選課記錄,學生越多,掃描工作量越大,所以通過增加實體數量即可完成測試.實驗依次隨機選取數據集中的200,400,600,…,8000個實體,分別統計不同實體數量情況下狀態數、規則數、支持度超過60%的規則數、支持度超過80%的規則數、支持度超過95%的規則數、規則掃描耗時、計算支持度消耗時間.

(1) 數據特征分析

實體數與狀態數關系如圖5所示.總體上看,狀態數隨實體數增加呈現對數增長趨勢.開始階段,隨實體數增加,狀態數迅速增加;當實體數增加到2 000左右時,狀態數增長明顯放緩.針對選課數據,可以解釋為25%左右的學生選課范圍覆蓋了全校大部分課程.

規則數隨實體數增加依然呈現對數增長狀態,關系如圖6所示.圖中 4條曲線分別為全部規則數、支持度大于60%、大于80%以及大于95%規則數,其中,支持度計算中未考慮定義7中的強度影響.隨著支持度要求的提升,規則數量增長愈加緩慢.針對測試數據集,這種趨勢表現出數據兩個特點:一是有一小部分實體的狀態序列是缺乏規律性的,可以解釋為選課的隨意性或者有課程重修,時效規則中環路較多,選擇合適的支持度即可過濾掉大部分這類規則;另一方面,數據又表現出大多數實體的狀態序列是較為規律和穩定的,只要支持度設定合理,可以用來實現較高可靠性的時效順序恢復.

Fig.5 Trend chart of the number of states increases with number of entities圖5 測試數據集中狀態數隨實體數增加變化情況

Fig.6 Trend chart of the number of rules with different supports varies with number of entities圖6 不同支持度的規則數隨實體數增加變化情況

(2) 考慮強度參數的規則支持度

參見定義7及相關解釋說明,部分高支持度規則重復出現次數是很少的,是個別現象甚至是特例,不足以作為規則用于數據修復.為了使測試更加客觀,實驗測試了規則強度對規則數量的影響.引入強度函數后,新的支持度為原支持度與強度函數的乘積.實驗中采用Logistic函數作為強度函數:

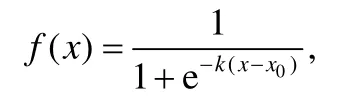
其中,k和x0應根據數據特征和具體需求設置:k>0,其值越小,f(x)增長越慢;x0≥0,當x=x0時,f(x)=0.5.加入x0的目的是使函數向右平移,以滿足函數f(x)值域為(0,1).本次實驗中,設定k=0.5,分別測試了x0=5,x0=10對規則數量及修復數據正確率的影響.x0=5時,當某條規則出現5次時,其強度函數值為0.5;出現10次時,強度已超過0.9;出現15次時,函數值已超過0.99.出現次數越多,強度值無限接近于1.

未考慮強度的規則數隨狀態數增長情況如圖7所示.理論上,n個結點的完全有向圖含有n(n-1)條邊,狀態數為結點數,規則數為邊數.但對于絕大多數數據集來說,用于時效規則提取的狀態都不會是無限的,應該是一個有限集合,這也決定了規則數量也是有上限、可預期的.在圖7中也可以明顯看出,高支持度規則數的增長速度是明顯慢于低支持度規則增長速度的.

Fig.7 Trend chart of the number of rules with different supports varies with number of states圖7 不同支持度的規則數隨狀態數增加變化情況

加入支持度強度指標后,規則數與狀態數關系如圖8所示.當實體數為8 000,k=0.5,x0=5時,支持度大于60%,80%,95%規則數分別是總規則數的 30.7%,23.7%,16.5%;x0=10時,上述 3個支持度的規則數分別是總規則數的21.7%,18.2%,13.7%,且3個百分比梯度更小,規則的集中度更高.可見:強度的設置清理了大量重復率低、時效代表性差的規則,大幅縮減了規則數量.x0的取值可根據噪聲粒度合理選擇,較大的取值雖然可以過濾更多低重復規則,但也可能把一些重復次數較少但有效的規則排除在外.

Fig.8 Low frequency rules are greatly reduced after considering rule strength圖8 考慮規則強度后低頻次規則大幅減少

(3) 提取規則算法效率測試

效率實驗中,主要記錄了提取規則耗時和整理規則耗時情況.整理規則的主要任務是對規則進行清理和計算規則支持度.提取(或發現)規則耗時與實體數增加呈線性關系,整理規則耗時隨實體數增加呈現對數增長趨勢.實際上,整理規則耗時隨規則數增長線性增加,規則數隨實體數對數增長(如圖9所示),所以整理規則耗時隨實體數對數增加.算法 1具體實現中使用了哈希表數據結構,計算規則支持度等處理效率非常高,能在 3 000ms數量級處理60萬條原始規則.而且算法1是可以進行并行化改造的,規則的提取可以分布式完成,滿足大數據集處理的時效性要求.

Fig.9 Efficiency test of rule discovery and rule post-processing圖9 規則發現和規則整理運行效率測試

3.3 數據時效修復結果分析

(1) 數據時效修復測試方案

(A) 依次設置時效修復規則的支持度S>60%,S>80%,S>95%,執行步驟(B);

(B) 在數據集1中依次隨機選取實體數N=200,400,600,…,8000完成時效規則的提取,執行步驟(C);

(2) 數據時效修復效率測試

實驗設置在數據集1中取不同數量實體用于規則提取, 采用相同的支持度(S>0.6)分別對數據集2的2000～8000條記錄進行時效修復實驗.實體數與記錄修復耗時關系如圖10所示.

Fig.10 Time-consuming of data currency repairing algorithm圖10 數據時效修復算法耗時情況

實體數增加到一定程度之后,時效修復耗時基本穩定不變.分析算法 2可知:由于時效修復中也采用了哈希表數據結構,理想情況下,每條記錄的時效修復耗時與實體數、規則數無關,為常數階復雜度O(1).實際測試中,普通PC可在800ms數量級完成8 000個實體記錄修復,執行效率可以滿足大規模數據時效修復要求.

(3) 規則支持度對數據修復正確率的影響

實驗設置在數據集1中取不同數量實體用于規則提取,分別采用不同支持度的規則(S>0.6,S>0.8,S>0.95)對數據集2的8 000條記錄進行時效修復實驗.實驗分兩輪:

· 第1輪測試中,強度函數k=0.5,x0=5;

· 第2輪k=0.5,x0=10.

分別測試強度函數x0的取值和不同支持度規則對數據修復正確率的影響.不同規則支持度下,修復 8 000條記錄正確率隨實體數增加變化情況如圖11所示.由圖可見:

· 第1輪實驗中,在實驗數據集上實體數2 000左右是個轉折點:在此之前,使用支持度S>0.6的規則修復正確率最高,使用支持度S>0.95的規則修復正確率最低;其后則逐漸反轉,規則支持度越高,時序修復正確率越高;

· 第2輪實驗中,轉折點出現在實體數3 000左右,且實體數較少時相較第1輪實驗的數據恢復正確率明顯偏低,體現出x0取值對低重復規則的過濾作用較強.

結合圖11可以發現:當實體數達到 2000～3000左右時,狀態數增長明顯放緩.產生這種情況的原因是:實體數小于一定閾值時,狀態數不足,此時強度函數中x0的取值對結果影響較為明顯,可用的高支持度規則少,數據修復正確率低;當實體數超過某一值后,狀態圖中的絕大多數結點都已出現,可用的高支持度規則增加,時序修復正確率提高.實驗結果表明:當用于規則提取的實體數量足夠多時,選擇支持度(S>0.95)時,數據時效修復正確率達93%左右,可滿足一般應用數據時效修復需求.

Fig.11 Trend chart of the accuracy of repairing with different rule-supports varies with number of entities圖11 不同支持度規則修復數據正確率隨實體數變化情況

(4) 規則強度對修復正確率的影響

實驗設置在數據集 1中取不同數量的實體用于規則提取,分別在考慮規則強度和不考慮規則強度情況下的支持度(S>0.6)對數據集2的2000～8000條記錄進行時效修復實驗.實驗結果表明,

· 考慮規則強度的情況下(k=0.5,x0=5),數據修復正確率波動小,修復數據一致性好,但是實體數少時正確率偏低,如圖12(a)所示;

· 未考慮規則強度時,數據修復正確率波動較大,但實體數少時正確率相對較高,如圖12(b)所示.

導致這種現象的原因是:實體數偏少時,高支持度規則數量不多,造成數據修復正確率波動較大;隨著實體數量增加,高支持度規則數量逐漸趨于穩定,數據修復正確率也趨于穩定.在考慮規則強度的情況下,選擇合理的支持度是穩定提高數據修復正確率的有效方法.

Fig.12 The effect of rule strength on data currency repairing accuracy圖12 規則強度對數據時效修復正確率的影響

4 小結

本文針對同一實體對應的多條記錄存在時間戳缺失或不精確條件下的數據時效修復問題進行研究,進一步明確了數據時效問題的相關概念和定義,給出了通用的狀態類型時效規則提取算法,不需專門領域知識即可完成基于時效規則的提取.研究還給出了基于時效規則的數據時效修復算法,并在真實數據集上對算法參數設置、運行效率、時效修復正確率進行了測試和驗證.時效規則提取算法直觀易于實現,時序修復算法效率、修復正確率較高,可滿足一般應用要求.

在此基礎上,下一步研究工作將重點集中在以下幾個方面:

(1) 研究在存在違背函數依賴、條件依賴等情況的非一致的數據集上的時效修復問題;

(2) 研究時序修復方法在檢測數據集可能存在的時效沖突中的應用,用以改進數據質量;

(3) 研究結合時效規則的函數依賴、條件依賴方法在數據質量評價中的綜合應用.