面向交通流量預測的多組件時空圖卷積網絡?

馮 寧,郭晟楠,宋 超,朱琪超,萬懷宇

1(北京交通大學 計算機與信息技術學院,北京 100044)

2(交通數據分析與挖掘北京市重點實驗室(北京交通大學),北京 100044)

智能交通系統(ITS)[1]正在大力發展,交通數據預測問題是其中的重要組成部分.車流量是反映公路運行狀態的主要參數之一,如果能夠提前準確地對車流量進行預測,事先對車輛進行疏導,可以提高路網的運行能力和效率,減少交通事故,降低人們的出行時間和成本,降低環境污染.

交通流量預測是典型的時空數據預測問題,不同類別的交通數據內嵌于連續空間,并且隨時間動態變化,因此,有效提取時空相關性對解決這類問題至關重要.圖1所示為流量數據(也可以是車速、車道占用率等其他交通數據)的時空相關性示意圖,時間維包含 3個時間片,空間維的 6個節點(A～F)表示公路的網狀結構.在空間維上,節點的交通狀況之間會相互影響(綠色虛線);時間維上,某節點歷史不同時刻流量會對該節點未來不同時刻流量產生影響(藍色虛線);同時,節點歷史不同時刻的流量值也會對其關聯節點未來不同時刻的流量產生影響(紅色虛線).可見,交通流量在時空維度都存在很強的相關性.而如何從這些復雜、非線性的時空數據中挖掘出隱含的時空模式,并對這些模式進行分析從而提取出有價值的信息,是時空數據挖掘任務的一項極大挑戰.

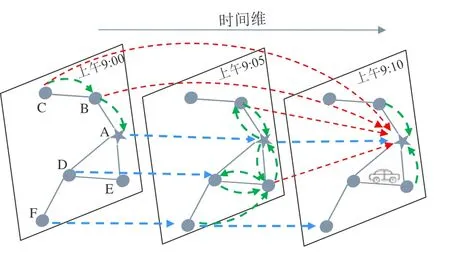
Fig.1 Spatio-Temporal correlation of traffic flow data圖1 交通流量數據的時空相關性

隨著交通行業的發展,道路上部署了許多攝像頭、傳感器等信息采集設備,這些設備擁有獨特的地理空間位置,不斷采集各類交通數據,如流量、車速、車道占用率等,積累了大量豐富的帶有地理信息的交通時間序列數據,為流量預測提供了很好的數據基礎.目前,已有很多學者在這類問題上進行了大量嘗試.早期的時間序列預測模型只能用于數據相對穩定、呈線性變化的預測問題,很難適應實際需求.隨后發展起來的傳統機器學習方法雖然能對更復雜的數據進行建模,但仍然很難同時考慮交通數據的時空相關性,而且這類方法的預測效果很大程度上依賴于特征工程,這往往需要依賴領域專家的經驗和大量的實驗.近年來,很多人將深度學習的方法應用于時空數據預測問題,如利用卷積神經網絡(CNN)可以有效提取網格數據的空間特征,但對于圖結構的時空數據的特征描述和時空相關性分析,目前仍然還在探索之中.

為了應對上述挑戰,我們提出了一種基于深度學習的交通流量預測方法——多組件時空圖卷積網絡(MCSTGCN)模型,使用基于時空卷積網絡的深度學習模型來處理交通路網這類圖結構數據,能夠同時有效捕獲數據的時空特性.該模型分別設置近期、日周期和周周期等 3個組件來描述交通數據的時空特征,最后將 3個組件的輸出進行融合得到最終的預測結果.本文的主要貢獻概括如下:

· 同時考慮并建模了交通流量數據固有的3種時間維特性,即近期依賴、日周期性和周周期性,并利用3個學習組件分別建模這3種特性;

· 提出了MCSTGCN模型,能夠直接從基于圖結構的交通數據中同時有效捕獲空間和時間維特征;

· 在真實的高速公路流量數據集上進行實驗,驗證本文提出模型的預測效果優于其他現有的預測方法.

1 相關工作

交通量預測問題歷經多年的不斷研究和實踐,取得了大量的成果.傳統的統計學方法有歷史均值法、自回歸積分滑動平均法(ARIMA)[2]等.歷史均值法是以歷史一段時間數據的均值為依據進行預測,ARIMA將預測對象隨時間推移而形成的數據序列視為一個隨機序列,用一定的數學模型近似描述這個序列.這類方法對復雜非線性的交通數據處理能力不足,因為它們都要求數據滿足一些前提假設,但實際中的數據往往很難滿足這些假設.K近鄰、支持向量機等機器學習方法能對更復雜的數據進行建模.采用K近鄰方法的思想是識別相似的交通狀況用于預測[3],而采用支持向量機方法的思想是通過核函數將低維非線性流量數據映射到高維空間后再進行線性分類[4].這類方法仍然無法同時有效考慮交通數據的時空相關性,且需要大量的特征工程.隨著深度學習在語音識別、圖像處理等領域取得的成果,越來越多的人將深度學習應用于時空數據預測問題.Zhang等人[5]設計了基于殘差卷積單元的ST-ResNet來對城市人流量進行預測,這種方法雖然提取了流量數據的時空特征,但將輸入限制為標準的2維或3維網格數據,因而不能用于圖結構的高速路網上的交通預測問題.

傳統的卷積神經網絡可以有效提取數據的局部特征,但只能作用于標準的網格數據.而圖卷積可以直接在圖結構的數據上實現卷積操作.目前,主流的圖卷積方法包括空間方法和譜圖方法.空間方法直接把卷積核應用到圖上的節點及其鄰域,這種方法的核心在于如何選擇節點的鄰域.Niepert等人[6]為中心節點啟發式線性選擇鄰域,將其映射為向量再進行卷積,在社交網絡任務中取得了不錯的效果;Li等人[7]在人體動作識別任務中引入圖卷積,提出多種劃分策略將節點的鄰域劃分為不同子集,通過控制子集的個數,保證不同節點可以共享卷積核權重.譜圖方法通過圖拉普拉斯矩陣將網格數據上的卷積操作推廣到圖結構數據上.Bruna等人[8]提出了一個通用的圖卷積框架,將拉普拉斯矩陣的特征向量變換到譜域,再通過樣條插值的方法近似求解;隨后, Defferrard等人[9]優化了該方法,將樣條插值替換成切比雪夫多項式的K階截斷近似求解,并證明了卷積核的范圍嚴格限制在中心節點的K階鄰居內,同時降低了模型復雜度;Seo等人[10]提出了圖卷積循環網絡(GCRN),但在特定設置下很難確定循環網絡和圖卷積的最佳組合;隨后,Li等人[11]成功地使用門控循環單元(GRU)和圖卷積進行長期交通預測;Yu等人[12]提出了一個帶有門控機制的圖卷積網絡,并應用于交通量預測問題.但這些模型都沒有考慮交通數據在時間維度上的周期性和趨勢性等多種固有特性.

交通流量預測問題的核心在于如何有效捕獲數據的時空維特征及相關性.圖卷積可以直接對圖結構數據進行特征提取,自動挖掘交通數據的空間模式.沿時間軸做卷積操作,可以挖掘交通數據的時間模式.因此,本文采用基于時空圖卷積網絡的深度學習模型,將二者結合起來同時捕獲交通數據的時空特性,有效解決交通流量預測問題.

2 問題定義

2.1 空間路網

我們將空間路網定義為無向圖G=(V,E,A),如圖2(a)所示,其中,V為節點集,|V|=N為節點個數;E為邊集,表示節點間的連通性;A∈?N×N為圖G的鄰接矩陣.設在空間路網G上的每個節點都會檢測F個采樣頻率一致的時間序列數據,即每個節點在每個時間戳都會產生一個長度為F的特征向量,如圖2(b)(數據歸一化后的示意圖)實線所示.

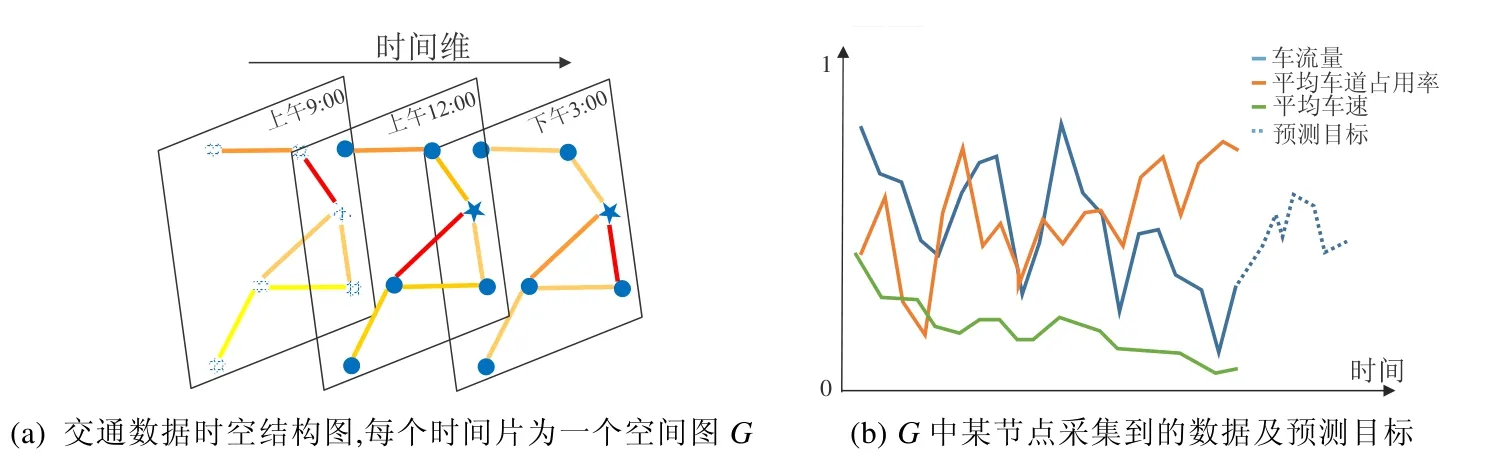
Fig.2圖2

2.2 流量預測

設路網G中各節點的第f∈(1,…,F)個時間序列為流量序列,未來某一段時間范圍內的流量為我們的預測目標.用表示第i個節點的第c維時間序列在t時刻的值,表示所有節點的第c維時間序列在t時刻的值,表示所有節點的第c維時間序列在τ時段內的值,表示所有節點的所有時間序列在t時刻的值,表示所有節點的所有時間序列在τ時段內的值.設是第i個節點在t時刻的流量值,已知路網上所有節點的歷史τ時段內的所有時間序列值X,我們的預測目標是未來所有節點在窗口長度為Tp的流量序列,其中,表示節點i的預測目標,如圖2(b)中的藍色虛線所示.表1列出了本文的符號約定.

Table 1 Mathematical notation表1 符號約定

3 基于深度學習的多組件時空圖卷積網絡

圖3展示了本文提出的多組件時空圖卷積(MCSTGCN)網絡的總體架構,它由3個主要部分組成,分別用來建模預測目標的近期、日周期及周周期信息(GCN:空間維圖卷積;Conv:時間維卷積;FC:全連接).例如,對某地下午2點的車流量進行預測,那么與預測時段直接相鄰的歷史1小時內的交通數據、對應的1天前及1周前下午2點的交通數據都會對該預測問題提供有用信息,而當天上午9點的交通狀況往往與預測目標關系不大.為了得到充足的時間維信息,同時減少處理不相關歷史信息帶來的開銷,我們設計了 3個組件分別用于描述交通數據的3種時間維特性:近期特性、日周期特性及周周期特性.

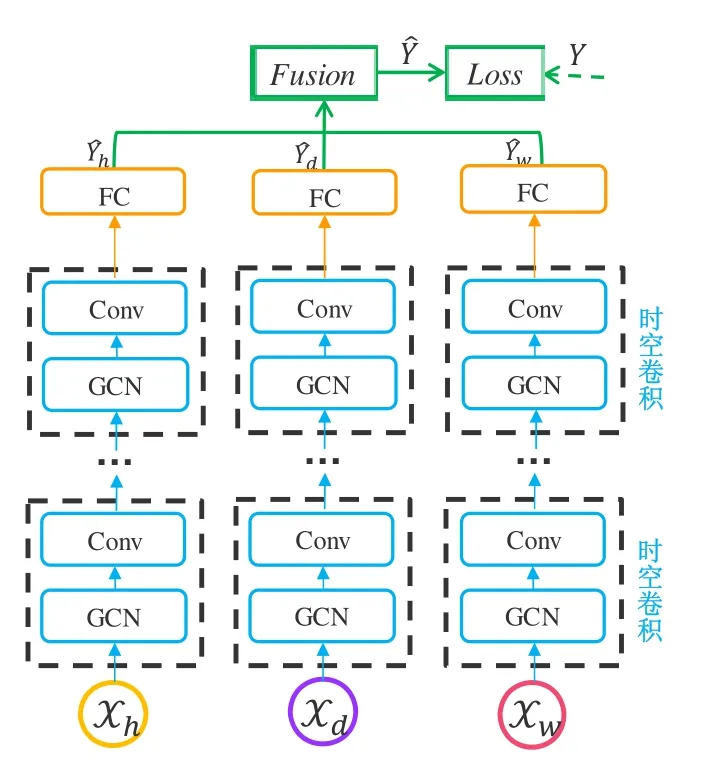
Fig.3 Architecture of MCSTGCN圖3 MCSTGCN模型架構圖

假設采樣頻率為每天q次,即時間序列上每天包含q個數據點.設當前時刻t0,待預測的時間窗口長度為Tp,我們沿時間軸分別截取長度為Th,Td和Tw的3個時間序列片段作為模型中近期、日周期和周周期3個組件的輸入,如圖4所示(設預測時段長度Tp為 1小時,Th,Td和Tw均取Tp的 2倍),其中,Th,Td和Tw均為Tp的整數倍.3個時間序列片段分別如下.

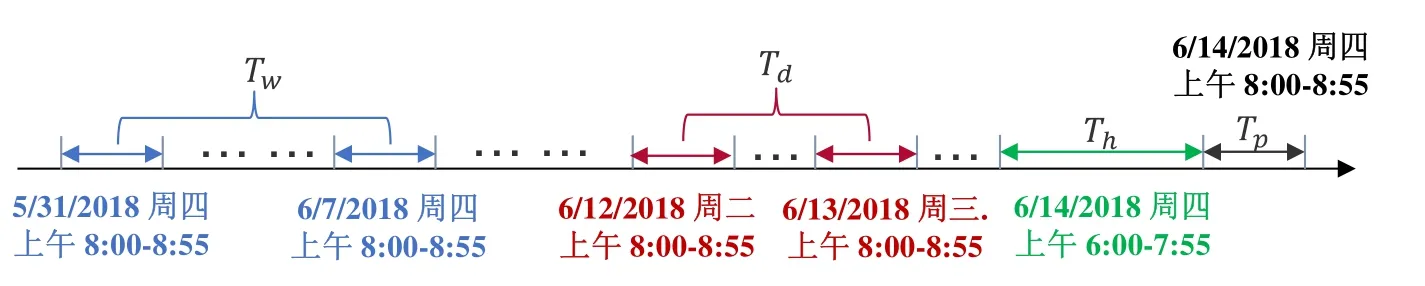
Fig.4 An example of constructing the input of time series segments圖4 輸入時間序列片段構建示例

3個組件共享相同的網絡結構,由時空卷積模塊(如圖5所示)和全連接層組成,其中,時空卷積模塊包括空間維度的圖卷積和時間維度的標準 2維卷積兩部分.模型最后將 3個組件的輸出結果基于參數矩陣進行融合,得到最終的預測結果.這種結構能夠有效捕獲交通數據的時間維和空間維特征及其時空相關性.

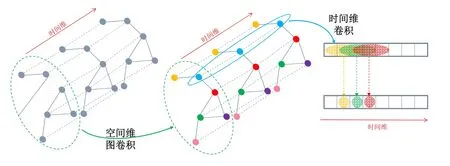
Fig.5 Architecture of spatio-temporal convolutions of MCSTGCN圖5 MCSTGCN模型的時空卷積結構

3.1 空間維圖卷積

我們首先只考慮某一時間片上的空間圖G,以了解空間特征的建模過程.在我們的模型中,采用譜圖方法[9]將卷積操作推廣到圖結構數據,將數據視為圖上的信號,然后直接在圖上對圖信號進行處理,來捕獲空間中有意義的模式和特征.

譜圖方法主要通過將圖轉化為代數的形式來分析圖結構,在本文中,我們主要關心圖結構中節點間的連通關系及相互影響,在譜圖論中,可以將一個圖用其對應的拉普拉斯矩陣來表示.通過分析拉普拉斯矩陣及其特征值就可以得到圖結構的性質.圖的拉普拉斯矩陣定義為L=D-A,其規范化形式為,其中,A為鄰接矩陣,IN為單位陣,度矩陣是節點度數組成的對角矩陣,.對拉普拉斯矩陣進行特征值分解L=UΛUT,其中,是L的特征值組成的對角矩陣,U是傅里葉基[12].以t時刻流量數據為例,圖信號為,對圖信號進行傅里葉變換可表示為.根據拉普拉斯矩陣的性質可知U是正交矩陣,因此得到逆傅里葉變換.圖卷積是利用定義在傅里葉域中對角化的線性算子來等價代替經典卷積算子[13]實現的卷積操作,用卷積核gθ對圖G進行卷積操作[9]:

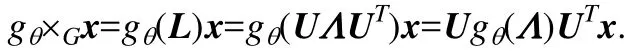
由于對圖信號進行卷積操作再做傅里葉變換等于對這些信號進行傅里葉變換后的乘積[14],上式可以理解為對gθ和x分別做傅里葉變換到譜域,然后對二者的變換結果進行乘法操作,再做傅立葉逆變換得到卷積操作的結果.

將圖變換到譜域實現圖上的卷積操作即為圖卷積,但當圖的規模較大時,直接對拉普拉斯矩陣進行特征值分解代價昂貴,因此,本文采用切比雪夫多項式近似展開求解:

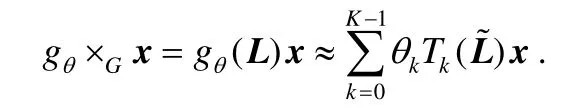
θk∈?K為切比雪夫多項式系數,表示拉普拉斯矩陣的最大特征值.切比雪夫多項式的遞歸定義:Tk(x)=2xTk-1(x)-Tk-2(x),其中,T0(x)=1,T1(x)=x.用切比雪夫多項式近似展開求解,相當于對圖中的每個節點采用卷積核提取了以該節點為中心的周圍 0～K-1階鄰居的信息[9].圖卷積模塊使用線性修正單元(ReLU)為激活函數,即ReLU(gθ×Gx).

以K=2為例,對每個節點提取其0～1階鄰居信息,對拉普拉斯矩陣特征值進行縮放使λmax=2,上述圖卷積操作表示為

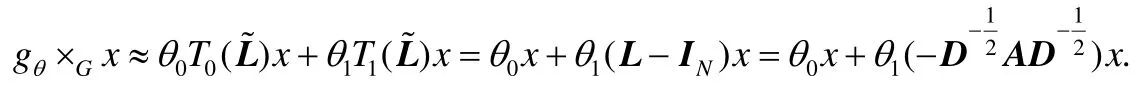
令θ0=-θ1=θ∈?以減少參數,則,圖上所有節點共享卷積核權重θ.同時,為避免數值不穩定、梯度爆炸或梯度消失[15],我們令,得到:.拓展到多維數據,第r層卷積的輸入數據是,其中:r∈{1,…,l}(l是時空卷積層數);Cr-1是第r層網絡的輸入數據的通道數,當r=1時,是輸入數據時間維長度,當r=1時,近期組件T0=Th(日周期組件T0=Td、周周期組件T0=Tw).對進行圖卷積操作,表示為,其中,是卷積核參數.

以Cr-1=1為例,圖6展示了圖卷積過程中對空間節點的0～1階鄰居信息進行提取的過程.圖6(a)為空間路網結構,圖6(b)為根據圖6(a)計算得到鄰接矩陣A和度矩陣及輸入數據的矩陣表示如圖6(c)所示,由此計算出用卷積核對數據進行圖卷積操作的結果如圖6(d)所示,其中,節點F在t=2時刻的值由原來的變為,即,輸入數據被其0～1階鄰居的信息更新.其他特征及卷積核同理,對整個輸入數據進行一次圖卷積操作,得到,每個節點被該節點的 0～K-1階鄰居的信息更新.

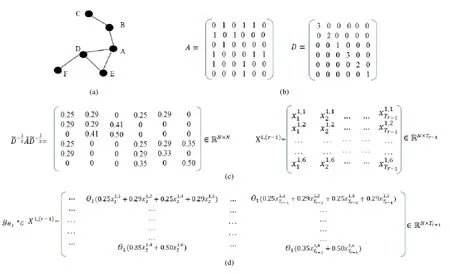
Fig.6 An example of graph convolutions and its matrix representation圖6 圖卷積示例及其矩陣表示

3.2 時間維卷積

通過空間維圖卷積操作對輸入數據的空間特征進行建模之后,再用標準 2維卷積捕獲時間維特征.我們用線性修正單元激活函數,以提取近期特征為例,得到(Ψ為時間維卷積核的參數),具體卷積過程如圖5所示.

經過一層時間維卷積之后,節點的信息被該節點相鄰時間片信息更新,而節點及其相鄰時間片信息在經過圖卷積操作后已包含其相鄰節點同時刻的信息.因此,通過一層時空卷積操作之后,就會捕獲到數據的時間維和空間維特征以及時空相關性.我們使用多層時空卷積,以提取時空維上更遠的信息,再通過全連接操作使時空卷積的結果與預測目標維數一致,全連接模塊同樣使用線性修正單元作為激活函數.

3.3 多組件融合

在本節中,我們將討論如何融合近期、日周期和周周期組件的輸出.以對整個路網周五上午 8點的流量進行預測為例,有些地方早晚高峰周期規律明顯,其日周期、周周期組件的預測結果更為重要;而有些地方不存在明顯的交通周期規律,日周期、周周期組件對預測目標起到的幫助較小.可見,不同節點受不同組件的影響程度是不一樣的,在融合不同組件的輸出結果時,其影響程度也應該不同.因此,應該從歷史數據中進行學習.融合后的最終預測結果表示為

其中,⊙是矩陣對應元素相乘的哈達馬積;Wh,Wd,Ww是學習參數,反映了近期、日周期、周周期這3種時間維特性對預測目標的影響程度.

4 實驗與結果分析

為了檢驗本文提出模型的性能,我們在兩個真實世界的數據集上進行了對比實驗.本節將對數據集和實驗設置進行說明,并對實驗結果進行詳細的對比分析.

4.1 數據集介紹

我們使用美國加利福尼亞州的真實高速公路數據集 PeMSD4和 PeMSD8來驗證我們的模型.PeMS是由Caltrans Performance Measurement System實時采集的高速公路交通數據,該系統擁有超過39 000個傳感器站,部署在加利福尼亞州高速公路系統的主要大都市區[16].數據集是基于 30s/次的頻率采樣得到的原始數據匯總成的以5m為時間間隔的樣本.數據集包含帶時間戳的車流量、平均車速、平均車道占用率這3個維度的特征及采集這些信息的檢測器的地理位置信息.

· PeMSD4:San Francisco Bay區域的數據,共包含29條路上的3 848個檢測器,我們選取時間范圍為2018年1月～2月的數據進行實驗,其中,前50天作為訓練集,后9天作為測試集;

· PeMSD8:San Bernardino區域的數據,共包含8條路上的1 979個檢測器,我們選取時間范圍為2016年7月～8月的數據進行實驗,其中,前50天作為訓練集,后12天作為測試集.

4.2 數據預處理

我們對道路上的檢測器進行篩選,去掉那些距離過近的檢測器,保證檢測器節點間距離大于 3.5英里.樣本以5m為時間間隔,因此,道路上每個節點每天包含288個數據點.用線性插值法填充缺失值.另外,對數據進行0均值標準化(zero-mean)操作x′=x-mean(x),即讓數據的平均值為0.

4.3 實驗參數設置

我們基于Pytorch框架實現了MCSTGCN模型,圖卷積使用32個相同大小的卷積核.時間維卷積同樣使用32個相同大小的卷積核,這些卷積核沿空間軸維度為1,沿時間軸維度為3,通過控制步長調整時間維長度.整個模型訓練時間大約為20s/輪.3個組件的輸入數據長度會對實驗結果產生影響,我們通過實驗選定Th=3,Td=1和Tw=1為最佳的組合.均方誤差是反映估計量與被估計量之間差異程度的一種度量,因此,本文采用該度量指標作為損失函數.

4.4 基準方法

我們將本文提出的模型與以下7種已有的時間序列預測方法進行比較.

· HA:歷史均值法,其預測值為近期歷史流量狀況的平均值.在本文中,我們使用最近12個時間片的平均值來預測下一個時間片的值;

· ARIMA[2]:自回歸積分滑動平均法,是時間序列分析中的一種經典方法;

· LSTM[17]:長短期記憶網絡,一種特殊的RNN模型.LSTM單元由細胞、輸入門、輸出門和遺忘門組成;

· GRU[18]:門控循環單元網絡[18],一種特殊的RNN;

· STGCN[7]:一種基于空間方法定義的時空圖卷積模型,采用了多種劃分策略將中心節點的鄰居劃分到不同子集,實現卷積核的參數共享;

· GCGRU[11]:一種將門控循環單元網絡與圖卷積網絡結合的方法;

· GLU-STGCN[12]:一種帶有門控機制的圖卷積網絡,在交通數據預測問題上取得了很好的效果.

本文采用均方誤差(RMSE)和平均絕對誤差(MAE)作為評價指標,具體計算公式下:

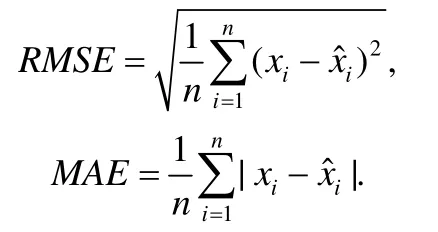
4.5 實驗結果及分析

我們將MCSTGCN模型在數據集PeMSD4和PeMSD8上與前述7種基準方法進行了比較,表2展示了對未來1h內的流量進行預測的結果.

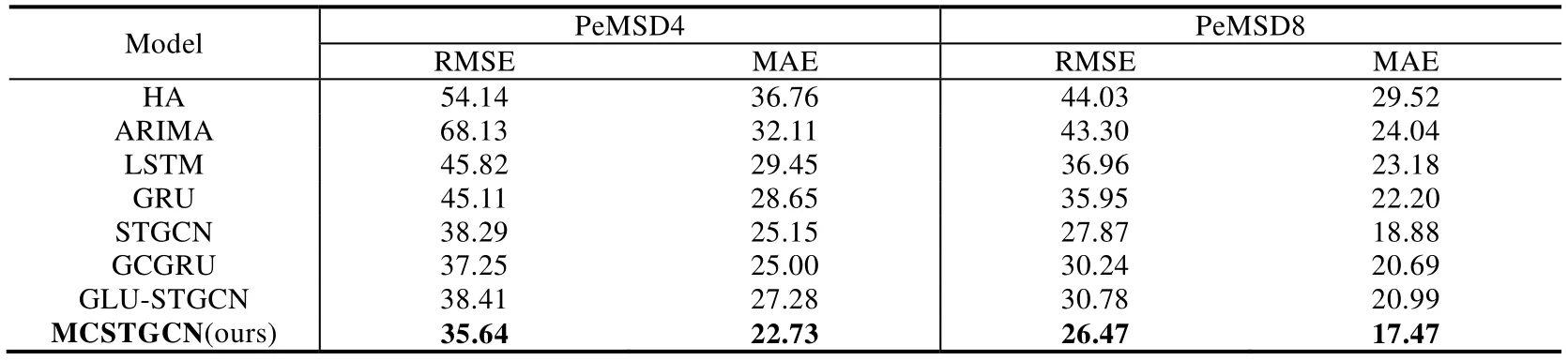
Table 2 Performance comparison of different approaches on the PeMSD4 and PeMSD8 dataset表2 不同方法在數據集PeMSD4和PeMSD8上的性能比較

從表2可以看出,我們的模型在兩種評價指標中均達到最佳性能.我們還可以觀察到,傳統的時間序列預測方法由于建模能力有限,預測結果并不理想.基于深度學習的方法獲得了比傳統方法更好的預測結果,而包含時空圖卷積機制的模型由于考慮了時空依賴性,預測結果要優于一般的深度學習模型.

此外,我們還比較了各種方法隨著預測時長的增長性能變化情況.我們以5m為間隔,讓預測時長從5m增長到1h,實驗結果如圖7所示.

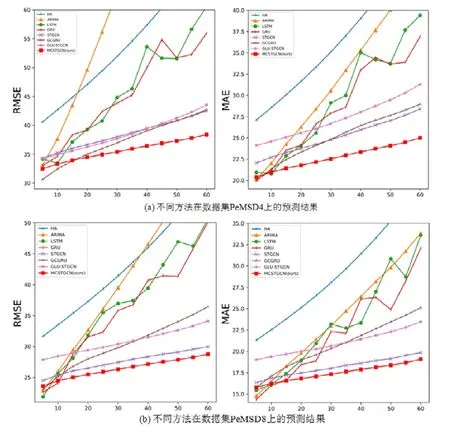
Fig.7 Performance changes of different methods along with the forecasting duration圖7 不同方法隨著預測時長的性能變化情況

從圖7可以看出,從整體上,隨著預測時長的逐步增大,預測難度越來越大,誤差整體呈上升趨勢.我們的MCSTGCN模型在短期預測中就取得了較優的的預測結果,這表明了多組件與時空圖卷積結合的策略能充分挖掘數據的時空模式;而隨著預測時長的增大,我們的模型預測誤差比其他方法增長更加緩慢,這是由于該模型顯式建模了時間維度上的多種周期特性,因而在中長期預測中顯示更加明顯的優勢.

最后,為了觀察每個組件的輸入數據的長度變化對預測結果的影響,我們在 PeMSD8數據集上將各組件的輸入數據長度分別設置為Th∈{1,2,3},Td∈{1,2,3},Tw∈{1,2,3}進行了實驗對比,其結果見表3.

Table 3 MAE with different component input lengths on dataset PeMSD8表3 不同組件輸入數據長度在數據集PeMSD8上的MAE

可以看出,Th的變化對預測結果影響較大,而Td和Tw影響相對較小.我們選定Th=3,Td=1和Tw=1為最佳的組合.

5 總 結

本文提出一種新穎的多組件時空圖卷積網絡 MCSTGCN,該模型結合圖卷積和標準卷積構造時空卷積塊來同時捕獲交通數據的時空特性.在真實的高速公路流量數據集上的實驗表明,本文提出的模型的預測效果優于其他已有的交通數據預測方法,驗證了該模型在捕獲時空特征及時空相關性方面具有優勢.事實上,除了高速公路流量預測任務外,我們提出的模型也適用于處理其他基于圖結構表示的時空交通數據.未來,我們將進一步通過注意力機制等策略來優化模型的網絡結構,進一步提升模型的預測能力.