CFD在螺旋槳飛機滑流影響研究中的應用

馬率，邱名，王建濤，繆濤，江雄

中國空氣動力研究與發展中心 計算空氣動力研究所，綿陽 621000

螺旋槳旋轉時，槳葉撥動空氣，一方面使空氣向后加速流動,另一方面又使空氣順著螺旋槳的旋轉方向扭轉流動，這種由于螺旋槳作用使氣流加速和扭轉的非定常復雜流動特性就是螺旋槳滑流效應。預測螺旋槳滑流對螺旋槳飛機氣動特性的影響一直是螺旋槳飛機設計中亟待解決且難度很大的問題[1]。

目前,CFD方法模擬螺旋槳滑流主要分為3種方式：一種是采用由動量-葉素理論發展而來的作用盤/激勵盤模型的定常方法[2-5]，一種是運用多參考坐標系(MRF)模型的準定常計算方法[6-7]，一種是基于雙時間推進法的非定常數值模擬。隨著計算機技術的飛速發展和計算方法的不斷進步，用基于雙時間推進法求解非定常雷諾平均Navier-Stokes(URANS)方程來數值模擬螺旋槳飛機滑流流場變得可行，相比于文中提到的前兩種方法，求解URNAS方程能更真實地描述螺旋槳裝機后槳葉旋轉運動的繞流細節，滑流尾跡發生及演化的非定常過程，從而有益于研究分析螺旋槳/機身干擾流動現象及背后的影響機理。

近年來，國外已有學者開始采用非定常數值模擬方法開展螺旋槳及滑流的氣動特性影響研究，例如Roosenboom和Heider[8]采用基于URNAS的DLR-TAU程序對A400M螺旋槳運輸機半模的翼身組合體進行了滑流研究，并用螺旋槳轉軸剖面處的渦量云圖與粒子圖像測速(PIV)試驗結果進行了詳細的流場對比，Ruiz-Calavera和Perdones-Diaz[9]分別采用試驗和CFX軟件對單獨螺旋槳和將螺旋槳安裝在飛機模型上的狀態進行了對比研究。在國內，非定常數值模擬螺旋槳滑流的研究起步較晚但發展較快，許建華等[10]用URNAS方程和動態重疊網格完成了單獨雙槳葉模型的流場數值模擬，許和勇和葉正寅[11]對某單發簡單螺旋槳飛機構型進行了URANS模擬研究，升力的計算結果高于試驗值4%左右；段中喆和劉沛清[12]開展了某型螺旋槳滑流對機翼氣動性能影響的數值研究；楊小川等[13]用非定常Euler方程數值模擬了螺旋槳飛機的滑流影響并進行了分析,夏貞鋒[14]用動態面搭接網格技術的非定常數值模擬方法和激勵盤理論研究了滑流對翼身組合體的影響及對開式轉子的非定常氣動特性。

以往的螺旋槳滑流影響研究往往集中在單槳的宏觀氣動力驗證、滑流對掃過部件的氣動力影響上，對于在滑流作用下的飛機部件氣動力和全機穩定性分析工作還很少。本文運用自主開發的大型三維可壓縮RANS方程解算器——PMBNS3D軟件,數值模擬了某螺旋槳飛機巡航構型低速特性下的流動，并與試驗結果進行了對比，計算值與試驗值吻合，驗證了程序的可靠性。并在此基礎上總結了螺旋槳滑流動對飛機全機及部件氣動特性和操控性能的影響規律，然后通過對螺旋槳滑流影響邊界區域的定義及分析，對滑流干擾現象以及背后的物理流動機理進行了研究和探索。

1 數值方法

1.1 控制方程

在慣性坐標下，針對任意運動控制體的可壓縮Navier-Stokes方程的積分形式為

(1)

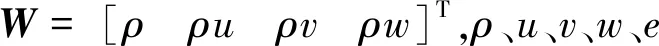
p=ρRT=ρ(γ-1)ε

(2)

(3)

式中：R為氣體常數；T為開爾文溫度;γ為氣體等壓熱容與等體積熱容的比值。無黏項的空間離散采用Roe平均迎風通量差分分裂格式，黏性項采用中心差分格式離散，計算分別采用了S-A一方程湍流模型和k-ω剪切應力輸運(SST)二方程湍流模型。非定常計算采用雙時間步方法，除了真實時間t之外，引入偽時間τ，好處是使原來只適用于定常計算的隱式時間迭代、局部時間步長、多重網格等方法都可以運用到非定常計算的偽時間迭代當中[15-16]。

1.2 多重網格方法

限制URANS非定常Navier-Stokes方程應用的一個重要因素是對計算資源的要求過高，對雙時間步方法來說，提高子迭代過程的收斂速率是衡量方法的一個重要指標，而在加速方法中多重網格法被證明是最有效的手段之一[17-18]。多重網格方法的原理是利用高頻誤差比低頻誤差更容易被迭代格式消除的特點，通過引入系列逐步粗化網格的辦法，將低頻誤差轉化為高頻誤差，消除各種誤差分量，再用套迭代技術將粗網格上的解返回到各級細網格上。多重網格法從理論上被證明至少對于線性橢圓型問題是一種最優化的數值方法，其計算工作量僅與網格節點數的一次方成正比，并且收斂速度與網格的尺度大小無關，從而特別適合應用在超大型工程數值計算問題中。本文采用了多重網格法中非線性方程的全近似格式(FAS)，套迭代技術為W循環。

1.3 動態重疊網格技術

在采用時間精確的數值方法求解中，網格運動是一個比較棘手的問題，較為成熟的方法是結構網格框架下的動態重疊網格方法[19-20]。由于不要求與各子網格共享邊界，網格塊之間允許重疊嵌套，從而極大降低了網格生成難度，彌補了結構網格對構型適應能力差的缺點,尤其是對于模擬螺旋槳相對機身運動的問題而言，能夠充分利用重疊網格動態插值的特點，當螺旋槳運動到新的位置時，只需要在流場空間重新建立重疊關系即可。重疊網格方法的核心是首先通過“挖洞”的方式剔除流場中落在計算域外的點，然后使用插值方法完成各子網格間必要的數據通信，提供各子網格流場求解所需的內邊界條件，從而實現全流場求解的匹配和耦合，它的計算主要包含以下步驟：① 重疊洞邊界的確定；② 貢獻單元搜索，建立插值關系。流場解算流程見圖1。

本文分別對帶動力全機的運動部件(槳葉及輪轂)和靜止部件(全機其他部分)生成各自的網格，槳葉網格隨槳葉一起運動，動態地與全機背景網格構成重疊關系，具體關系見圖2，另外運動的螺旋槳網格在旋轉過程中，背景網格的洞點和洞邊界不會發生變化，即在運動過程中背景網格只需要搜索一次洞點和洞邊界，然后在不同時刻確定洞邊界點在運動部件網格中新的插值位置即可。

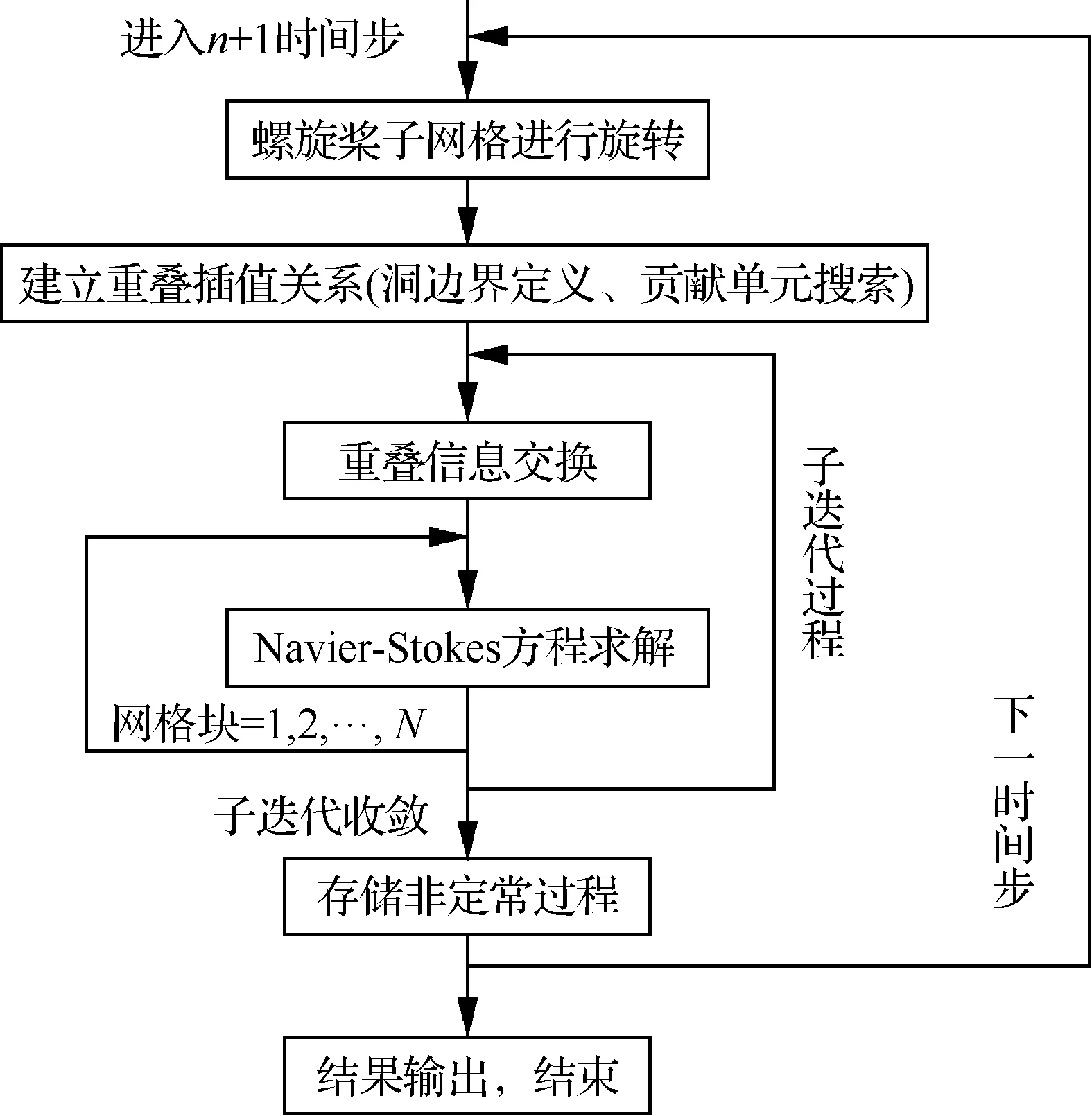
圖1 動態重疊網格數值計算流程圖Fig.1 Flowchart of dynamic chimera grids in numerical simulation

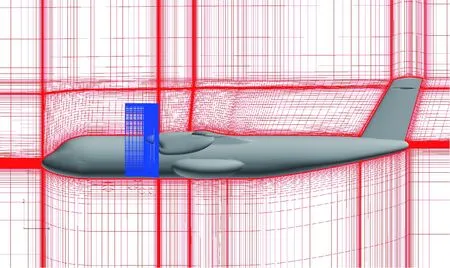
圖2 槳葉網格和全機其他部分的重疊關系Fig.2 Overlapping relationship between propellers and airplane grids

1.4 并行化計算

并行計算采用基于消息傳遞接口(MPI)的并行化算法，用區域分割方法將計算域映射到多個CPU上分別進行計算[21-22]。利用MPI技術實現消息傳遞，建立了滿足負載平衡的自動網格剖分方法，對隱式格式而言，每個網格塊“內邊界”值由相鄰塊處前一時刻的值來確定，對每塊獨立進行隱式求解，然后再根據通量守恒原理對相鄰塊重合點值進行修正。此外，各區塊網格還可以同時采用多重網格法等技術手段來提高整體計算效益。

在并行計算之前，需要將網格比較“平均”地分配到各個計算節點上，使各節點的負載大致平衡。由于計算網格采用多塊結構網格方法，在網格塊數小于節點數或者現有網格分塊不足以使負載平衡的情況下，對最大塊進行剖分，剖分需要滿足兩個條件，一是沿最大維數方向進行剖分，這樣保證信息交換量最少；第二要求剖分后網格滿足多重網格計算條件，如果最大維數方向滿足不了該條件的話就沿次大維數方向進行剖分，依次進行，按這種方法劃分的網格可以在各計算節點上進行多重網格計算，提高整體計算效率[23]。在網格剖分過程中，本文將網格單元數偏差控制在7%以內，這樣既能滿足負載平衡的要求，同時又不會把網格分得過于零碎，增加額外的通信需求。

在發展了動態重疊網格的快速自動查詢方法基礎之上，實現了重疊網格挖洞、插值關系建立的完全并行化。其中找插值關系的具體過程可以描述如下：對任意插值點而言，首先在本節點查找貢獻單元，在沒有找到的情況下將該插值點信息發送到其余各個節點上，由這些節點同時查找該插值點的貢獻單元，如果找到將該貢獻單元信息返回，則建立兩個節點之間的消息傳遞關系。這種做法的最大好處就是去掉了所謂的根節點，即任何節點的重疊網格計算不須收集網格全局信息，降低了單節點的內存要求，同時避免了單個節點計算重疊插值關系，其余節點等待的局面，提高了計算效率。

2 滑流對螺旋槳飛機宏觀氣動特性的影響

某螺旋槳飛機巡航無動力及帶動力構型如圖3所示，模型及計算的基本參數包括：模型縮比為1∶12，機翼面積為0.462 6 m2，機翼平均氣動弦長為0.201 25 m，試驗風速V=30 m/s，螺旋槳轉速n=4 977 r/min，名義拉力系數CT=0.15，機身迎角α=-4°～20°(2°一個間隔)，機身側滑角β=0°。

螺旋槳旋轉方向為雙發同向順時針旋轉(飛行員視角),為了模擬黏性附面層的需要，第1層網格距離物面的距離約為3×10-5m，滿足y+=O(1)，湍流模型采用了k-ωSST二方程湍流模型。無動力全機網格采用半模的對接網格方法，網格單元總數約為1 400萬，無動力全機單個定常計算狀態采用16核并行計算，迭代計算20 000步取收斂結果，耗時約為24 h。

全機網格規模約3 500萬，流場計算是以螺旋槳停止旋轉時的定常狀態作為初場，從此開始進行螺旋槳旋轉的非定常計算，計算采用在慣性坐標系下求解URANS方程的方法，在時間上計算采用雙時間步方法，每個真實時間步槳葉在周向運動了3°，即每個旋轉周期包含真實時間步數120步，每個真實時間步內的子迭代步數為40步，采用隱式LU-SGS(Lower-Upper Symmetric Gauss-Seidel)方法進行迭代，空間格式采用Roe通量差分分裂方法。單個非定常計算狀態采用64核并行計算，加速比為48，并行效率約為75%，迭代計算2 520個真實時間步數(螺旋槳旋轉21轉)，取一個周期內平均的氣動力作為最終結果。圖4給出了迎角α=0°時全機氣動特性隨真實時間步迭代的收斂曲線，可以看見升力系數CL在計算到約1 100步(螺旋槳旋轉約9轉)后呈良好的周期性化，而俯仰力矩系數Cm約1 600步(螺旋槳旋轉約13轉)后才收斂較好。圖5給出了0°迎角下周期性建立以后的子迭代殘差收斂曲線，可以看到密度殘差L2模下降了近2個量級，顯示了較好的子迭代收斂性。

值得一提的是，由于位于槳盤后方的飛機機翼對上游來流產生了阻擋作用，螺旋槳在對空間做功的同時，空間壓力場也會對螺旋槳施加一個反作用力，這樣使得安裝在飛機上的螺旋槳拉力相比名義上的單槳拉力要大，本機巡航狀態計算模擬得到的螺旋槳拉力系數為0.166 2，相比名義拉力系數0.15增大了10.8%，見圖6。

同時扭矩系數由原來的0.080增加到了0.093，增大了約16.2%，由于扭矩的相對增幅比拉力更大一些，所以螺旋槳裝機后的效率有小幅降低。圖7給出的是巡航構型無動力和帶動力全機低速試驗和計算所得的全機氣動特性隨迎角的變化，需要指出的是為了和試驗結果對比，圖中帶動力的升力系數CL和阻力系數CD曲線扣除了槳葉的直接拉力，而俯仰力矩系數Cm曲線則是加入了槳葉的俯仰力矩。從試驗和計算結果的對比情況來看，升力系數在線性段的總體偏差不超過2%，在失速點附近因為機翼上出現的分離區導致計算與試驗出現一些偏差；阻力系數計算結果相對試驗值而言整體偏大，但偏差基本控制在8%左右，偏大原因應該來自于數值計算解的耗散行為以及采用全湍流模型帶來的摩阻增加；俯仰力矩曲線趨勢對比良好，在線性段帶動力情況的計算值與試驗值相當吻合，而在勺型區域計算值與試驗值差別較大，只有帶動力情況的計算值與試驗值出現拐點的迎角一致；升阻比K曲線的計算結果與試驗值趨勢相似，但由于阻力的計算值總體偏大導致計算結果的升阻比小于試驗值。

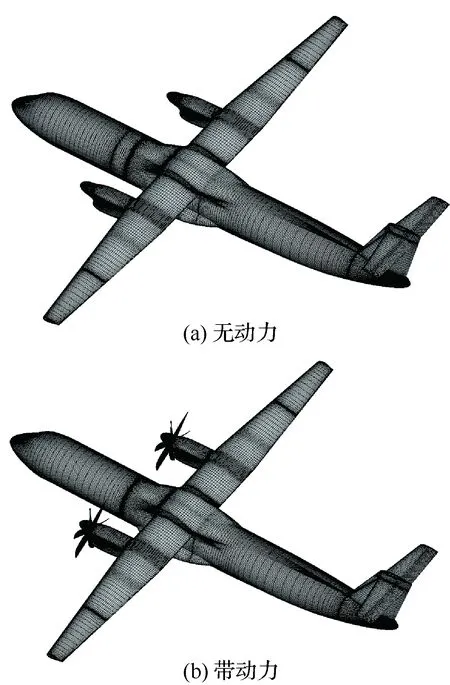
圖3 全機無動力及帶動力構型物面網格Fig.3 Grid of airplane surface without and with propellers

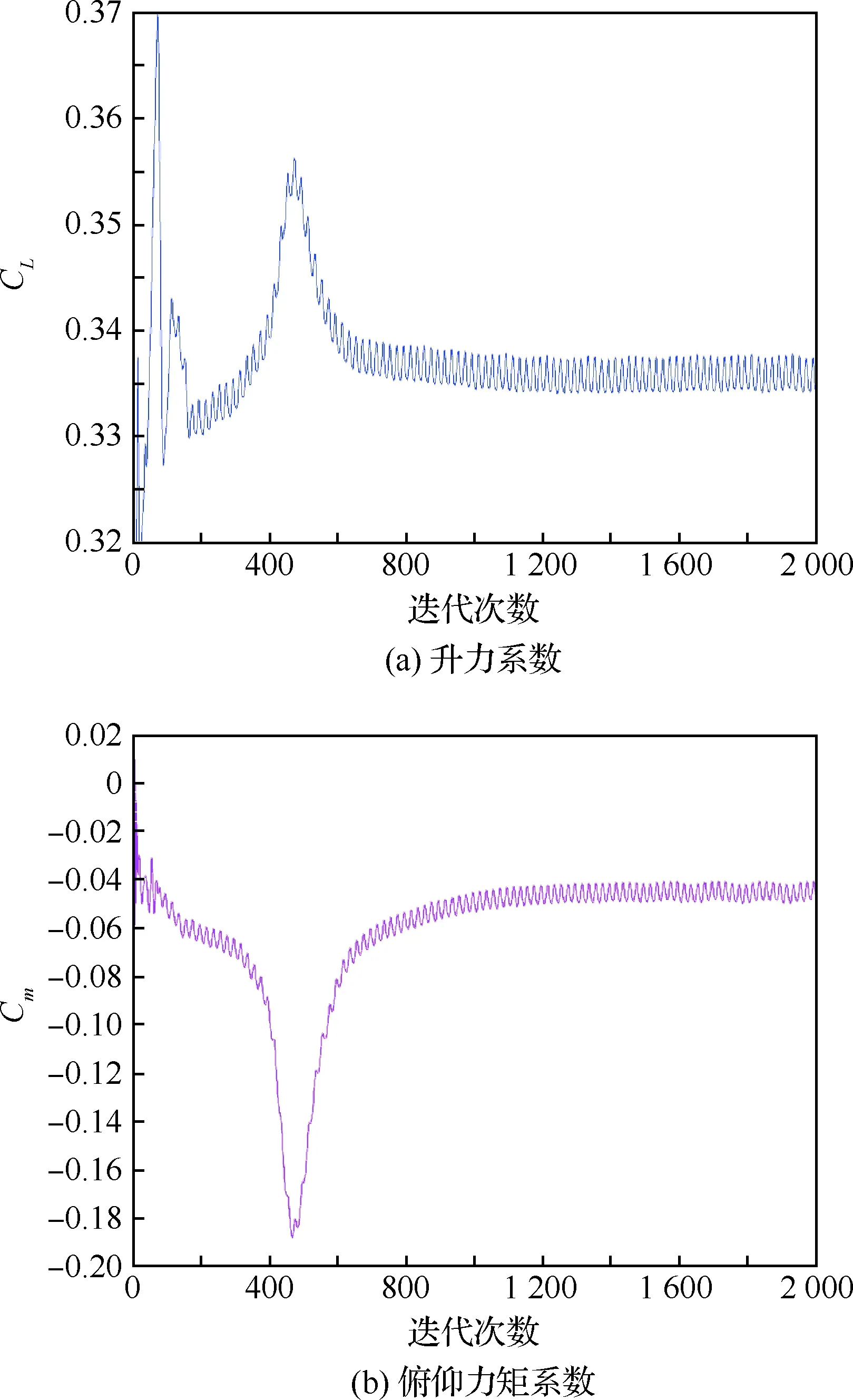
圖4 全機氣動特性隨真實時間步的收斂曲線(α=0°)Fig.4 Convergence history of airplane’s aerodynamics characteristics vs time step (α=0°)

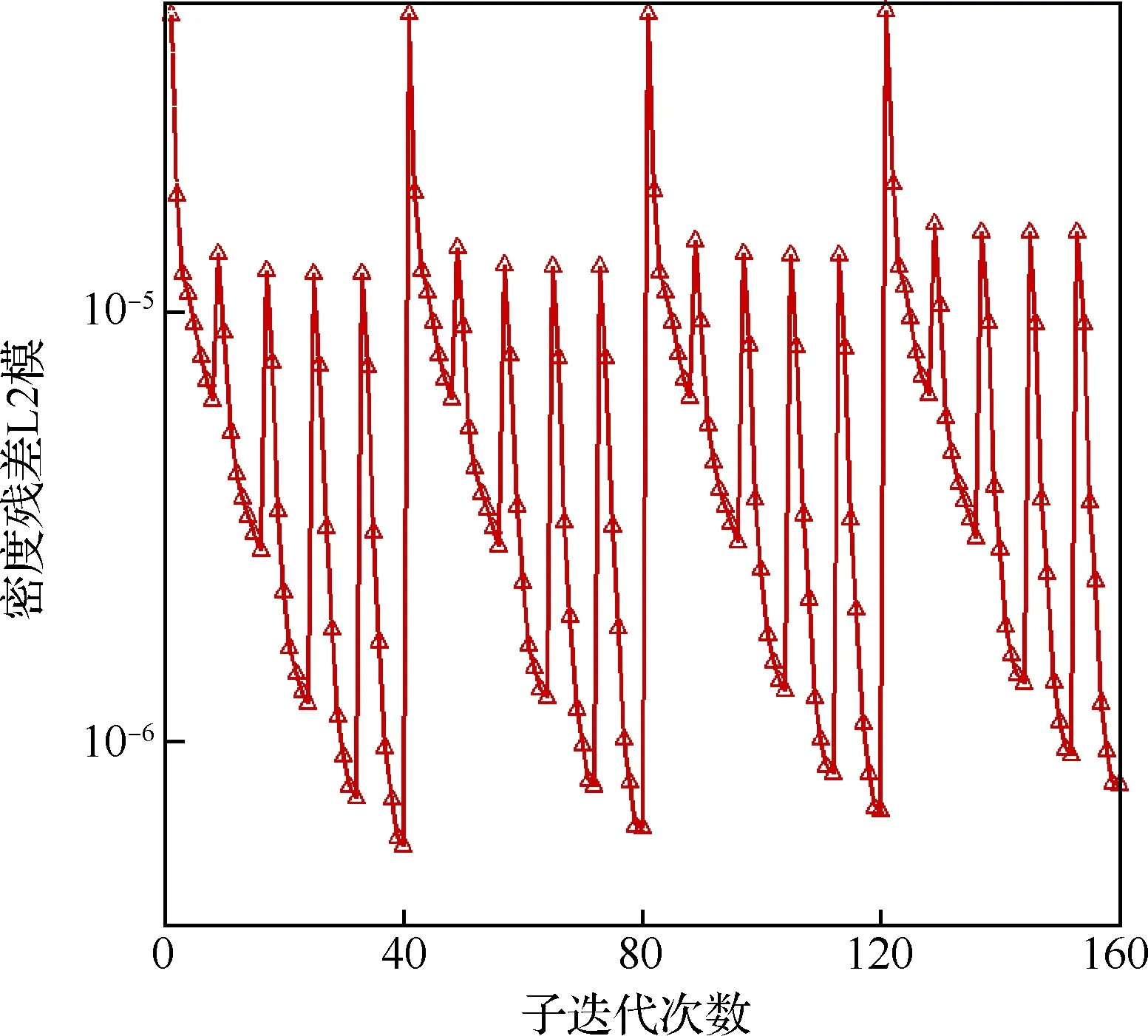
圖5 子迭代的殘差收斂曲線(α=0°)Fig.5 Convergence history of sub-iteration residual (α=0°)

圖6 計算得到的螺旋槳裝機拉力系數Fig.6 Computed thrust coefficient of propeller loading on airplane

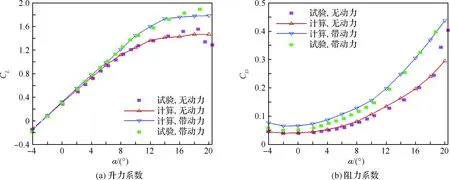
圖7 全機無動力與帶動力的氣動特性變化(n=4 977 r/min)Fig.7 Variation of airplane’s aerodynamics characteristics (without and with propellers, n=4 977 r/min)

在滑流作用影響下，全機升力、阻力系數隨著迎角的變大有明顯提升，例如在迎角4°以前，升力和阻力增量變化的絕對值都不太大，但在迎角4°以后，隨著迎角增大，升阻系數的增量也開始迅速放大，比如迎角12°時升力系數增幅達到19%，阻力系數增幅達到42.2%。而俯仰力矩系數斜率的絕對值小，說明帶螺旋槳動力的全機俯仰安定性對比無動力有所降低。

圖8給出的是對全機氣動特性起主要貢獻的部件隨迎角的變化情況，可以看到在滑流影響下，全機升力和阻力增量主要來自機翼變化的貢獻；滑流的扭轉給機身和發動機吊艙帶來明顯的側力影響，機身側力的非線性導致了全機側力在迎角增大后的振蕩特性，在后面的流場分析中可以看到滑流拖出的尾渦干擾是造成部件側力的主要原因；在不考慮螺旋槳自身的俯仰力矩情況下，全機俯仰力矩的變化主要來自于平尾和機身的貢獻，在滑流影響下左右平尾產生的俯仰力矩并不對稱且隨著迎角的增大它們的差別也在變大。

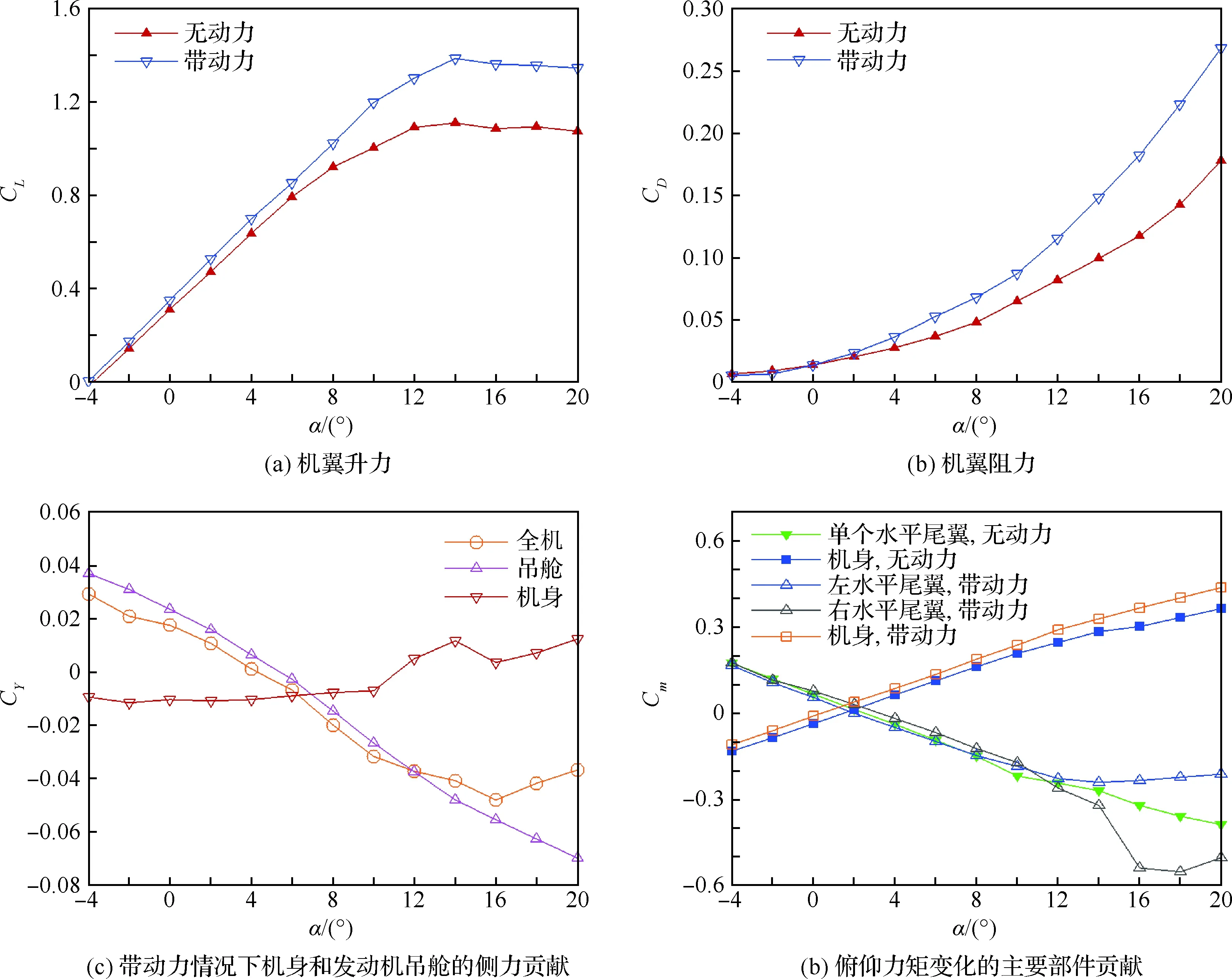
圖8 無動力和帶動力全機氣動特性的主要貢獻部件Fig.8 Parts of main contribution in airplane’s aerodynamics characteristics(without and with propellers)

3 滑流干擾的機理分析

3.1 滑流對全機物面的影響

圖9給出了無動力和帶動力巡航構型隨迎角變化的物面極限流線圖。與無動力構型相比，由于螺旋槳的轉動給氣流注入了能量，在2°小迎角條件下，短艙后面的分離被抑制，從而使得逆流向分離渦明顯減弱；8°迎角時短艙處流動分離區明顯被抑制，整流鼓包背部的回旋渦不再對稱，受到左側螺旋槳的旋轉影響被顯著削弱并向右側機翼偏移，展向分離消失；14°迎角時機翼外翼段出現了由翼梢引起的大面積展向分離，螺旋槳轉動帶來氣流偏轉效應的增強重新誘發了整流鼓包背部及右側機翼根部的較大面積弦向分離。造成以上現象的原因經過分析認為：首先螺旋槳的轉動會給氣流注入能量，但同時也會帶來氣流的偏轉效應，這樣就造成了機翼上表面克服弦向逆壓梯度的能力增強，即氣流弦向流動分離被抑制，但氣流的偏轉效應造成的側洗流場同時對機翼的展向分離帶來復雜影響，這與螺旋槳的旋轉方向密切相關，一般在滑流旋轉與機翼翼尖渦方向同一側時，機翼的展向分離會有所提前，反之，會推遲機翼展向分離。

由于低速迎角2°為典型狀態，下面對該狀態進行細節上的分析，圖10給出了低速巡航迎角2°時無動力及帶動力機翼的弦向截面站位壓力系數，由于螺旋槳的轉動給氣流注入了能量，滑流區域機翼上的動壓和靜壓都有所增加，在圖10中表現為駐點壓力增加，即壓力系數的正峰值明顯超過1而大于無滑流狀態；其次，由于氣流的旋轉，滑流區域機翼上的局部迎角發生顯著改變，滑流對短艙對稱兩邊機翼剖面的當地氣流迎角的影響作用也是不同的，反映在飛機前視圖中可以看到機翼前緣壓力在吊艙兩側出現了明顯的不同變化。參照圖10中對稱于吊艙兩邊的截面站位壓力系數比較，在槳葉上行一側Y=3 240，-5 500 mm處，機翼前緣的吸力峰在螺旋槳滑流影響作用下明顯增大，這對提升機翼的升力和減小阻力帶來了有利影響，但是在槳葉下行一側Y=5 500，-3 240 mm處，機翼前緣的吸力峰消失甚至在下翼面出現負壓力值(圖中機翼弦向站位x/c≈0～0.15處屬于向下壓力峰的作用范圍)，該處會抵消動壓升高對這部分機翼升力的作用。

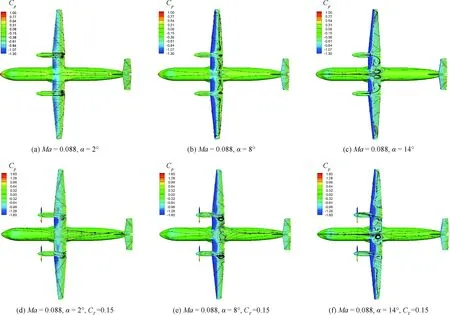
圖9 全機巡航狀態物面壓力系數和極限流線隨迎角變化情況(無動力和帶動力)Fig.9 Pressure coefficients and streamlines on cruise state airplane’s surface vs angle of attack (without and with propellers)

圖11反映的是無動力及帶動力機翼的展向截面站位壓力系數，η為展向站位系數可以發現在機翼的前緣位置，滑流對當地的壓力系數有著非常明顯的改變，而隨著流動在弦向的發展，螺旋槳滑流對機翼的影響沿展向是逐漸減弱的，在機翼后緣位置附近時，展向上的壓力分布除了在吊艙位置有所不同外，其他地方的分布與無動力狀態相似。

圖10 全機無動力和帶動力不同機翼弦向站位的壓力系數分布(Ma=0.008,α=2°,CT=0.15)Fig.10 Cp distributions for different stations located on wing chordwise (without and with propellers Ma=0.008,α=2°,CT=0.15)

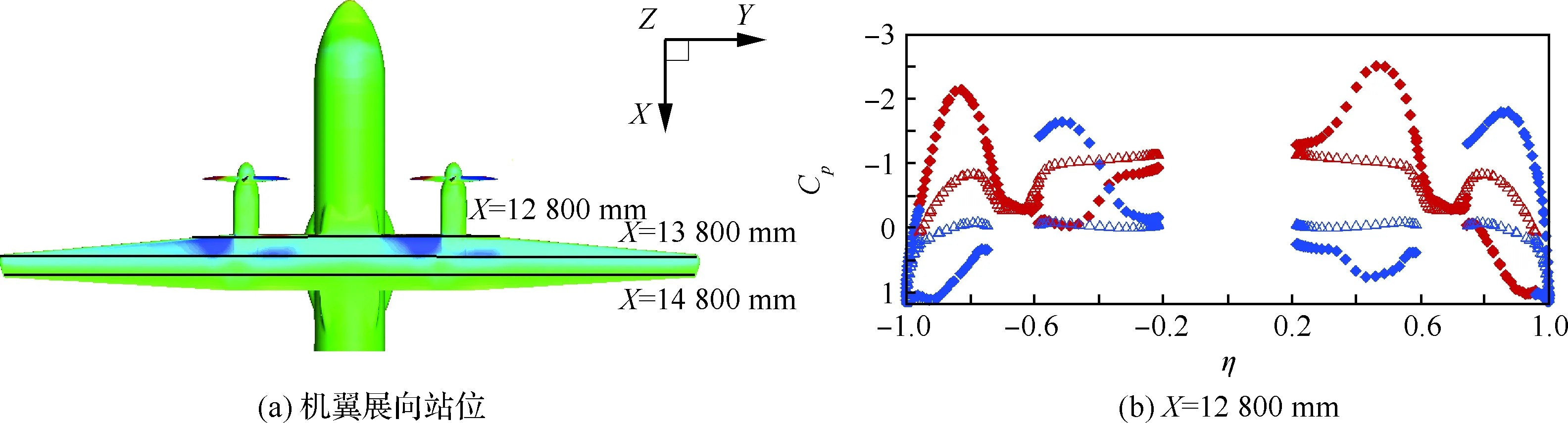
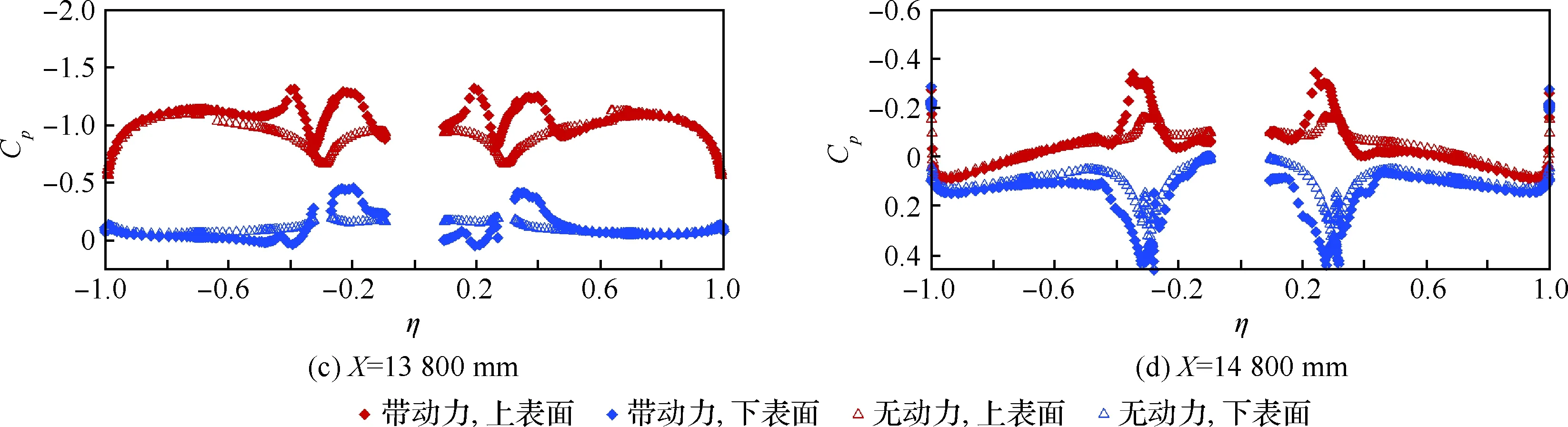
圖11 全機無動力和帶動力不同機翼展向站位的壓力系數分布(α=2°)Fig.11 Cpdistributions for different stations located on wingspan direction(without and with propellers, α=2°)

3.2 滑流對空間流場的影響

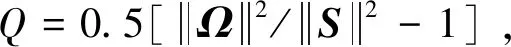
圖13給出的是螺旋槳轉軸位置Y=-4 370 mm處的弦向剖面的Q值云圖，可以看到螺旋槳槳葉卷起的尾跡渦和由輪轂和發動機吊艙產生的渦結構，槳葉的尾跡渦隨尾跡圈數的增加，旋渦直徑增大，旋渦強度減弱，而發動機短艙產生的渦從物面脫出后呈狹長的條狀帶，尤其是下翼面吊艙后部的分離渦強度大且貫穿到了機身尾部。

圖12 帶動力巡航狀態空間渦量等值面Cp圖Fig.12 Iso-surfaces of Q-criterion colored by Cp on cruise state with propellers

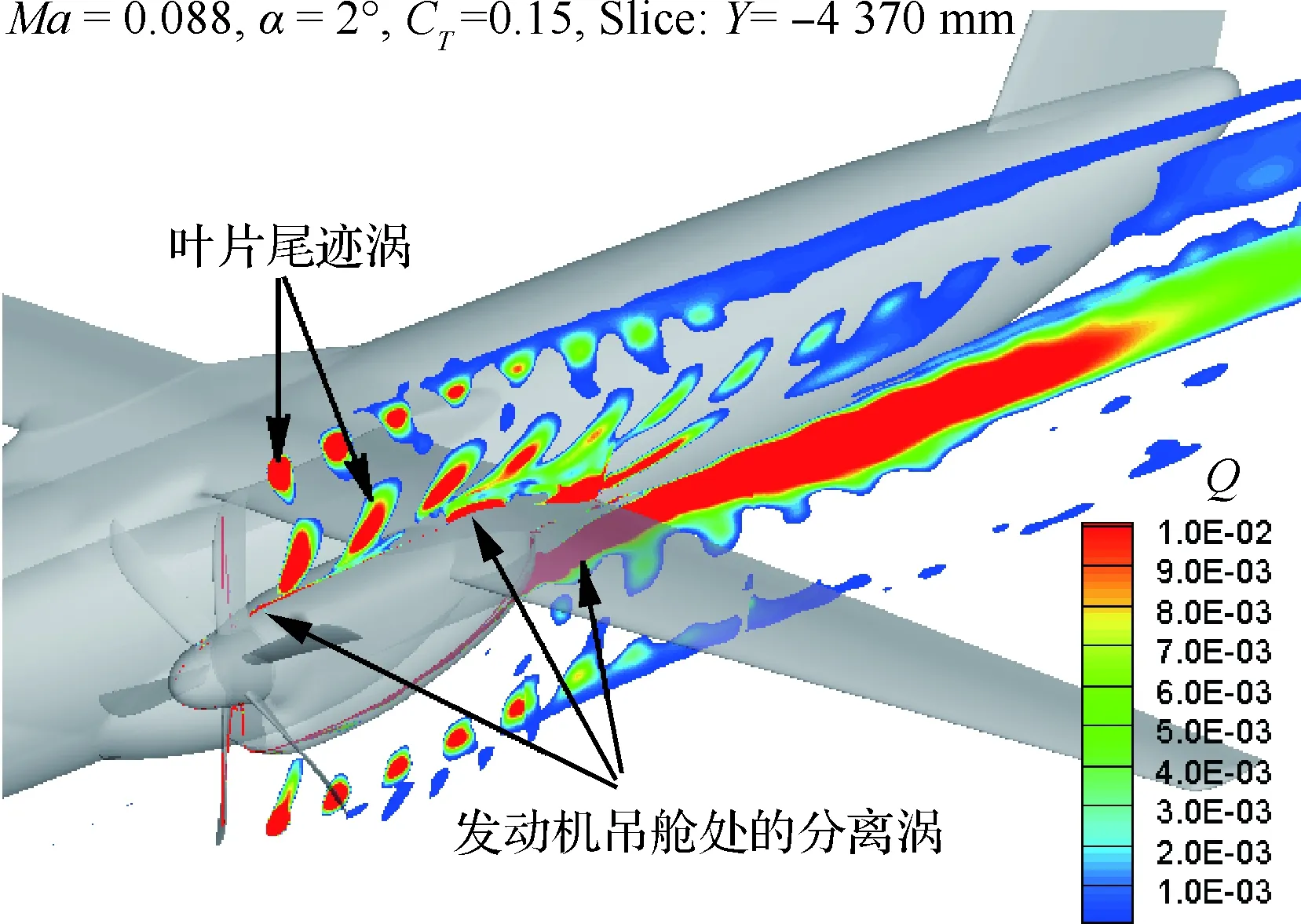
圖13 螺旋槳轉軸位置弦向剖面的渦量分布Fig.13 Vorticity contour at propeller rotation axis chordwise

在飛機開始設計階段就需要考慮螺旋槳滑流對掃過飛機的氣動操縱面的影響，最好能避開滑流影響區域，如確實無法避免則需迫切知道滑流對當地流場的影響。但由于滑流和射流相似，在空間發展過程中不斷與周圍空氣相混合，并受到黏性耗散，使得滑流向外擴散減速并不斷“模糊”其邊界，滑流流管沿流向發展的巨大畸變對滑流影響的分析工作帶來了巨大困難。水平尾翼如果部分或完全浸沒在螺旋槳滑流中，會承受較高的動壓，從加速作用的角度來看，這會增大尾翼有效升力線斜率，加強尾翼對穩定性的貢獻；同時螺旋槳槳葉的旋轉對流場帶來了洗流的作用——不限于滑流的流管，而是近似遍及整個流場，壓強分布(以及隨之的氣動力和力矩)與無滑流時有很大的不同。圖14～圖16分別給出了不考慮螺旋槳自身力矩情況下，有/無動力的全機在2°迎角時各部件的力矩系數貢獻圖,可以看到在滑流影響下，機翼和吊艙存在低頭力矩，而機身和右側平尾存在明顯的抬頭力矩，左右平尾俯仰力矩差別巨大的原因是由于滑流對它們產生了明顯的不對稱下洗作用，此時平尾對飛機縱向穩定性的貢獻是下降的；飛機的左偏航力矩貢獻主要來自機身和立尾，左右吊艙和機翼的偏航力矩各自反向近似抵消；全機的滾轉力矩主要來自于飛機左右機翼滾轉力矩的不對稱性，由于螺旋槳同向旋轉的原因，機翼升力偏置導致左側機翼升力相對于飛機重心的力臂距離比右側機翼升力更長，這樣即使在左右機翼升力相近的情況下,左側機翼產生的滾轉力矩自然會更大，可見滑流使飛機部件的氣動特性明顯復雜化。

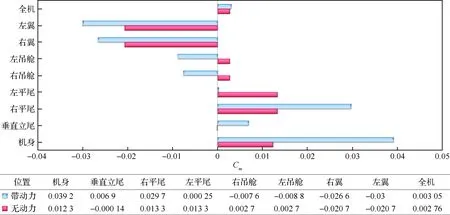
圖14 無動力和帶動力的部件俯仰力矩系數貢獻(α=2°)Fig.14 Parts contribution in airplane’s Cm (without and with propellers, α=2°)

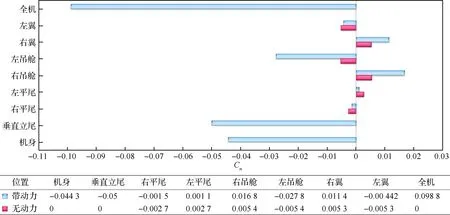
圖15 無動力和帶動力的部件偏航力矩系數貢獻(α=2°)Fig.15 Parts contribution in airplane’sCn (without and with propellers, α=2°)

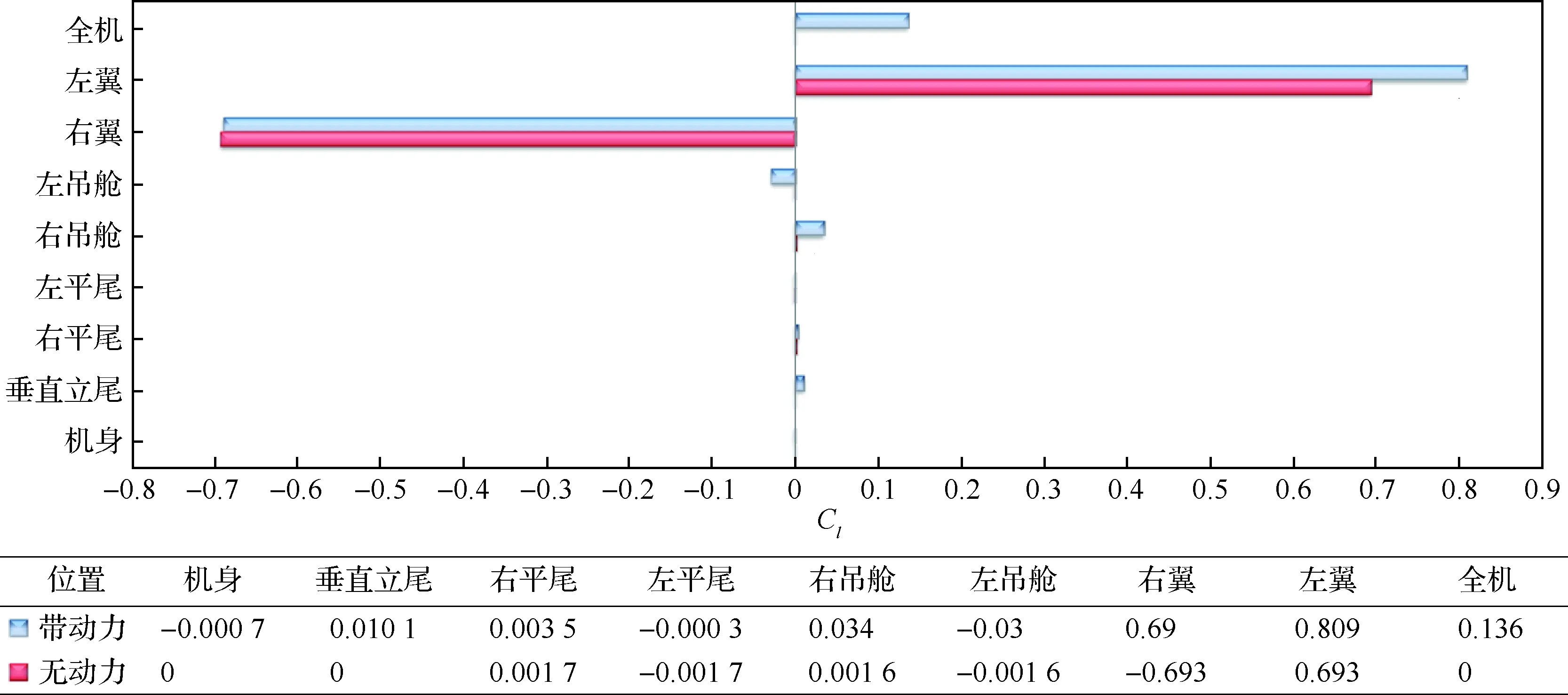
圖16 無動力和帶動力的部件滾轉力矩系數貢獻(α=2°)Fig.16 Parts contribution in airplane’s Cl (without and with propellers, α=2°)

本節前文中曾分析到滑流對流場的影響主要是來自加速作用和洗流,并且滑流為非定常的周期性變化流場，為了研究滑流的周期時均影響效果，本文采用有/無滑流不同情況下對比當地動壓增量來定義滑流的加速效應邊界，對比當地氣流角增量來定義滑流的洗流效應邊界，期望通過對滑流起主要影響作用的參數分解來判定滑流的影響區域。為了達到以上目的，需要將螺旋槳停止旋轉時定常狀態的流場和螺旋槳正常旋轉的非定常滑流的周期時均流場進行對比，得到兩者間的加速作用和洗流的增量變化。圖17～圖19分別給出的是在滑流影響作用下，空間流場不同截面的動壓增量Δq、當地迎角增量Δα和當地側滑角增量Δβ的變化情況。

圖17中的動壓增量Δq為無量綱量,可以發現空間中除槳葉卷出的滑流流管以外的地方動壓增量Δq近似為0，流管中機翼上下翼面附近處的動壓增量達到0.004左右，相比流場遠處來流的動壓q增加了一倍以上(遠場來流動壓q=0.003 87)，動壓的變化在向下游發展的過程中逐步減弱，由于飛機采用T尾布局形式，遠離了動壓劇烈變化區域，動壓變化對平尾位置沒有明顯的影響。圖18給出的是有/無滑流情況下當地氣流迎角增量Δα的空間剖面圖，可以明確看到滑流在空間上下洗流的影響情況，在槳葉后方的機翼吊艙兩側，槳葉上行側的Δα=7°～15°，下行側的Δα=-5°～-14°，而當流動經過機翼后，機翼后方的絕大部分區域下洗被明顯增強，只有位于槳葉上行側的機翼下表面后方區域有較大的上洗，而在空間流場中的平尾前方區域可以看到右側平尾的前方有約-2°左右的下洗增量，左側平尾的前方卻有約0.5°左右的上洗增量，這就導致了前文中提到的左右平尾俯仰力矩差別巨大的現象，同時右側平尾產生明顯的抬頭力矩，導致飛機縱向靜安定度下降。圖19反映的是有/無滑流情況下當地氣流側滑角增量Δβ的空間剖面圖，能夠看到滑流對空間流場側洗的影響，對于順時針旋轉的螺旋槳，機翼上面的滑流向右偏斜，下面滑流向左偏斜，在機翼后匯合起來，一般在機翼上仍近似圓形，離機翼后緣越遠，畸變越大，而立尾上左右側面Δβ在-5°～5°范圍呈不對稱變化，最終導致立尾有較大的右向側力和左偏航力矩。

圖17 帶動力巡航狀態動壓增量變化的空間剖面圖(α=2°)Fig.17 Incremental of dynamic pressure for different sections in flow field on cruise state with propellers (α=2°)

圖18 帶動力巡航狀態當地迎角增量變化的空間剖面圖(α=2°)Fig.18 Incremental of local angle of attack for different sections in flow field on cruise state with propellers (α=2°)

圖19 帶動力巡航狀態當地側滑角增量變化的空間剖面圖(α=2°)Fig.19 Incremental of local angle of sideslip for different sections in flow field on cruise state with propellers (α=2°)

4 結 論

對有/無滑流影響作用的某雙發同向旋轉螺旋槳飛機進行了巡航構型低速狀態的數值模擬，與試驗結果進行了對比,并對滑流的影響作用開展了詳細的分析，得到了以下結論：

1) 在現有計算條件下，線性段范圍內升力系數與試驗數據的誤差能控制在2%左右，阻力系數計算結果相對試驗值偏大，但誤差能基本控制在8%左右，俯仰力矩曲線在線性段與試驗值趨勢一致，但在勺型區域開始與試驗值有較大偏差。

2) 從宏觀的氣動力特性來看，在不計入槳葉直接氣動力情況下，受滑流影響的全機升力系數、阻力系數有明顯提升，它們主要來自機翼變化的貢獻，且隨著迎角的變大，升、阻系數的增量也開始放大；俯仰力矩的變化主要來自于平尾和機身的貢獻，左右平尾俯仰力矩呈現巨大的不對稱性，全機俯仰力矩系數斜率的絕對值減小；同向旋轉的滑流不對稱性使機身和立尾產生了明顯的附加偏航力矩,使機翼產生了附加的滾轉力矩。由于非對稱滑流帶來的非對稱氣動力，飛機的操縱效能相比無動力時嚴重下降，這就要求飛機在飛行過程中要不停調整各操縱面進行氣動力補償。

3) 螺旋槳后拖出的滑流改變了機翼的流態，其影響大致可以分為兩個方面：首先增加了滑流區機翼上的動壓，產生了一個升力增量和誘導阻力增量；其次改變了機翼上的局部迎角，使滑流區內螺旋槳上行槳葉側有效迎角增大(相當于誘導出一個機翼正彎度)，從而在機翼上誘導出一個正升力增量，同理滑流區內螺旋槳下行槳葉側有效迎角減小(誘導出一個機翼負彎度)，該處會抵消動壓升高對這部分機翼升力的作用。

4) 螺旋槳滑流對飛機機翼的失速影響也非常復雜。概括來說，首先螺旋槳的轉動會給氣流注入能量，這樣就造成了機翼上表面克服弦向逆壓梯度的能力增強，即氣流弦向流動分離被抑制，但螺旋槳也會帶來氣流的偏轉效應，它造成的側洗流場會對機翼的展向分離帶來復雜影響，這與螺旋槳的旋轉方向密切相關，一般在滑流旋轉與機翼翼尖渦方向同一側，機翼的展向分離會有所提前，反之，會推遲機翼展向分離的出現。

5) 本文采用有/無滑流不同情況下對比當地動壓增量和當地氣流角增量來定義滑流的加速效應和洗流效應邊界，采用該方法能較好地捕捉和解釋由于滑流對飛機尾翼干擾而使得飛機方向安定性呈現的很大非線性現象，增進了滑流對掃過飛機部件的氣動干擾作用機理的認識。

致 謝

感謝中航工業第一飛機設計研究院許瑞飛給予的幫助。