考慮故障風險的動車組部件機會維修優化策略
王 紅, 熊 律, 何 勇, 蔣祖華
(1. 蘭州交通大學 機電工程學院, 甘肅 蘭州 730070; 2. 上海交通大學 機械與動力工程學院, 上海 200240)
在激烈的市場競爭體制下,預防性維修策略的重要性和復雜性越來越受關注。在過去的數十年間,生產設備維修費用快速增長,據統計,在不同工業生產領域,其維修費用占據生產費用的15%~70%[1]。作為一般預防性維修策略(PM)研究的核心內容,為生產設備制定科學合理的預防性維修計劃受到了越來越多的重視。
文獻[2]采用機會維修策略將風機關鍵部件的維修有機的結合起來,從而實現分攤固定維修成本的目的;張耀周等[3]根據維修效果和外部環境工況,提出了設備的衰退演化規則,并利用設備停機的組合維修機會,建立了多設備維護優化調度的聯合區間軸策略;廖雯竹等[4]針對設備可靠度隨役齡和維修次數的增長而降低的實際情況,提出了一種基于可靠度的順序預防性維修模型。以上文獻在對設備的PM進行研究時,設備的故障危害僅局限于故障維修費用和停機損失費,即只考慮經濟損失[5-6]。然而對于運行中的動車組,某些部件如果發生突發故障,則其故障危害可能不僅僅局限于經濟損失,輕則導致動車晚點,重則可能導致重大的鐵路運營安全事故。所以,對高速鐵路動車組這類運行速度快、載客量大的運輸設備,在衡量其故障后果時,不能僅停留在經濟損失層面。文獻[7]根據部件故障對系統安全性影響的大小,進一步將部件分為關鍵部件和輔助部件,對關鍵部件采取以可靠性為中心的維修策略,但文中對部件的重要程度僅局限于定性分析。文獻[8]在研究港口設備的PM時,綜合考慮了可用度和維修成本率,提出了一種動態預防性維修策略,并考慮到設備故障導致集裝箱內產品變質和帶來的違約以及時間問題,但對部件維修效果的刻畫較單一,即在部件的設計壽命周期內只有一種預防性維修方式。但是,依據我國現行的高速鐵路動車組檢修制度,除了對到達壽命周期的部件執行更換操作之外,更多的是采用“多級別非完美”維修策略。
本文首先對動車組部件PM作了基本的問題描述和假設;其次,對兩級非完美故障率演化規則進行了詳細地闡述,并建立了部件故障風險的評價函數和維修總成本模型;然后,建立了部件層PM優化模型,根據對該模型的求解得出各部件的預防性維修可靠度閾值,以及對應的PM計劃,進而引入機會維修里程窗ΔL的概念,利用動車組停機的組合維修機會,對關聯部件的維修作業計劃進行合并,從而得到系統層多部件預防性機會維修策略(POM)下的維修計劃;最后選取動車組某機械系統進行算例分析并得出結論。
1 基本假設
我國現行的動車組檢修制度將動車組的檢修分為五個等級,其中四級修程時會對某些部件進行更換。動車組每運行2萬km獲得一次檢修機會,因此選擇動車組整車運行到偶數里程時對部件進行維修。部件在里程區間(0,lmax)內共進行了N次預防性維修,部件i的第j次維修時機為li,j=2v,其中,v=0,1,2,…,N,li,j-1到li,j為部件i的第j個預防性維修周期。
基于所研究的內容,作出如下假設:
(1) 部件的初始工作狀態為全新。
(2) 部件只有在動車組整車停機檢修時才獲得預防性維修的機會。
(3) 部件之間的故障率分布函數不存在關聯關系。
(4) 故障維修可以使部件恢復工作且維修資源充足。
(5) 在一個完整的壽命周期內,對部件的預防性維修只采取高級維修和初級維修兩級非完美維修方式。
2 部件層預防性維修優化建模
2.1 兩級非完美維修故障率演化規則
Zhou[9]結合文獻[10]提出的役齡遞減因子和文獻[11]提出的故障率遞增因子,給出了混合式故障率演化模型,其故障率演化規則如下
λi,j+1(l)=bi,jλi,j(l+ai,jLi,j)
( 1 )
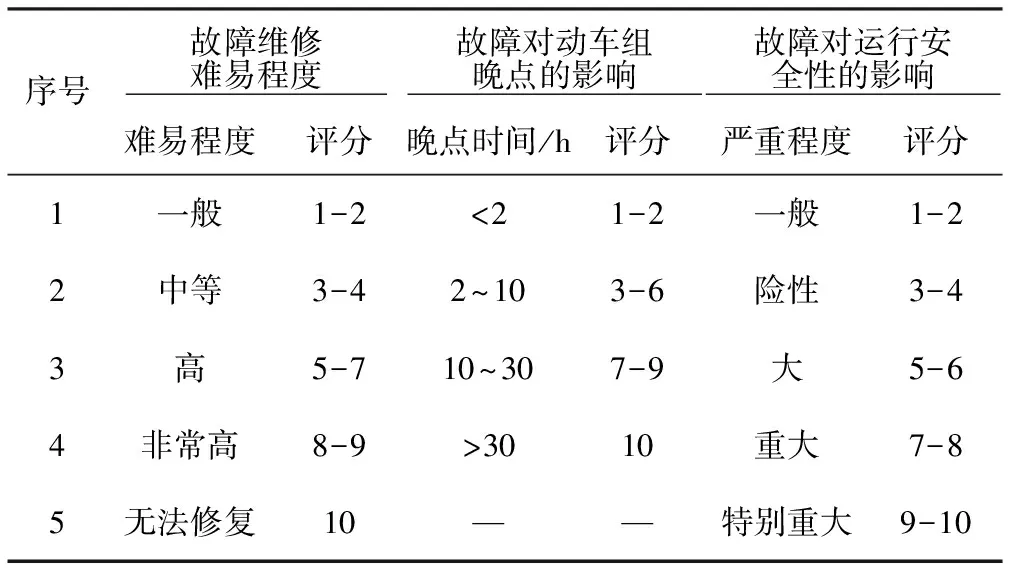
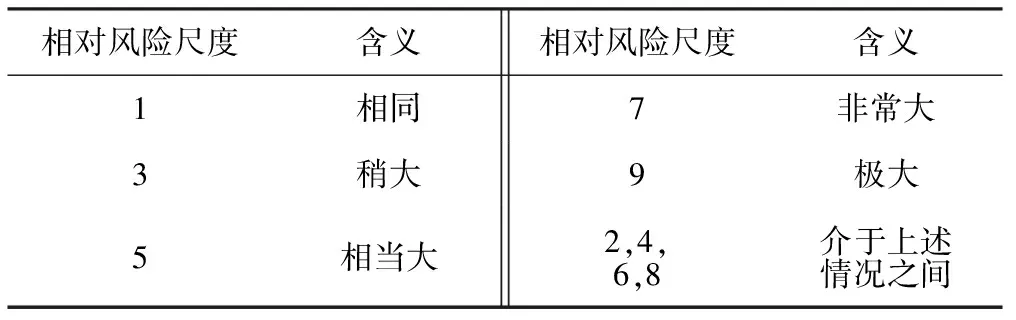
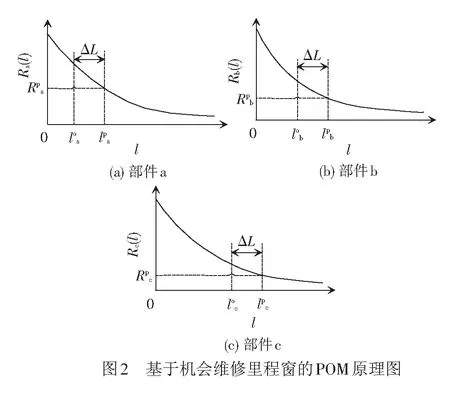
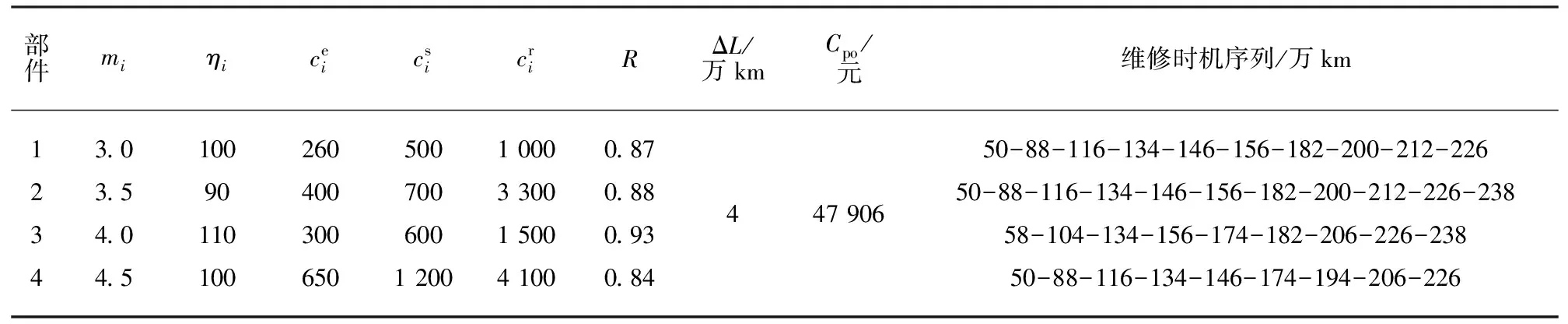
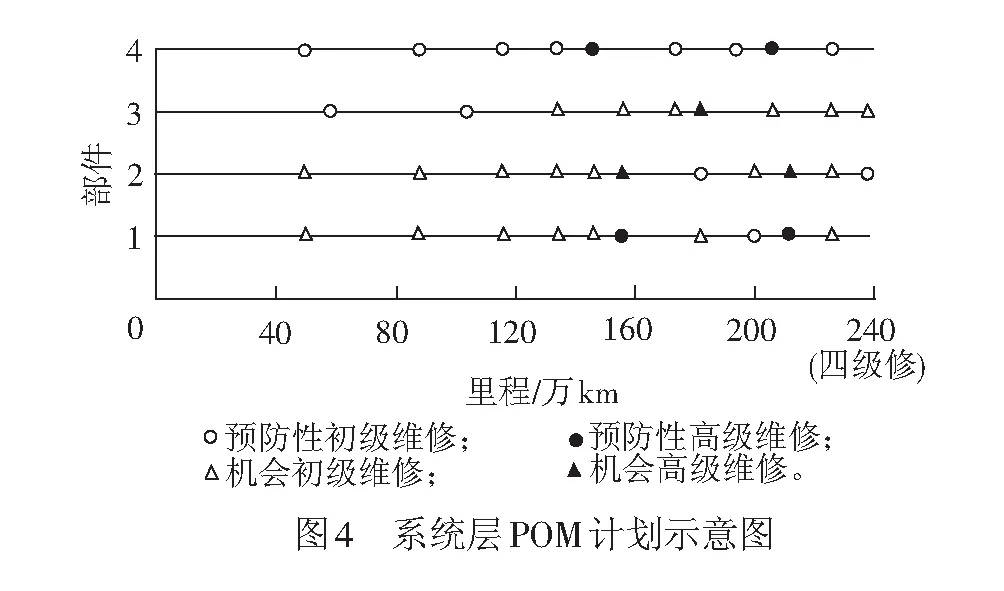
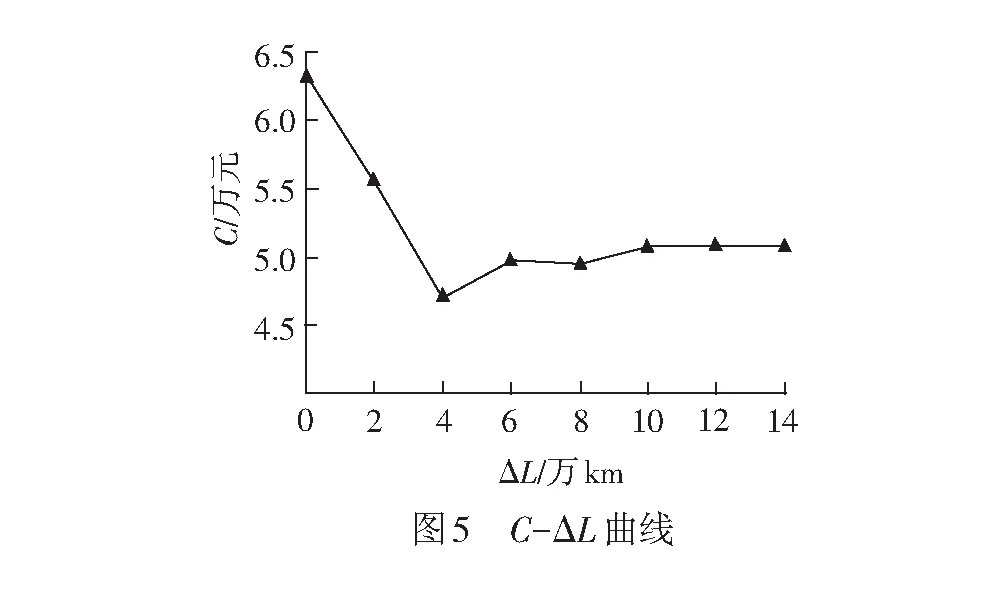
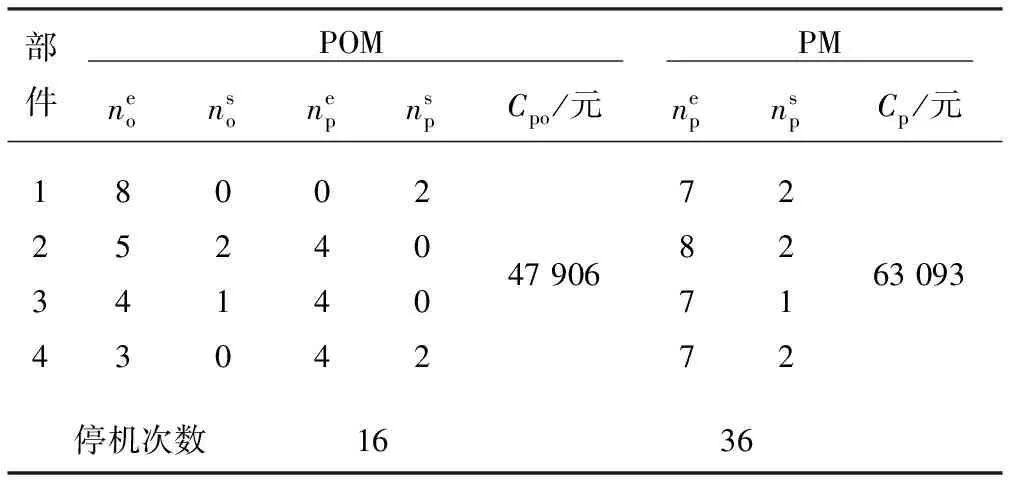
0 式中:ai,j為役齡遞減因子;bi,j為故障率遞增因子;Li,j為相鄰2次預防性維修之間的里程間隔,且有Li,j=li,j-li,j-1;λi,j為故障率函數。 據既定的預防性維修策略,在壽命周期內對部件的預防性維修方式只有高級維修和初級維修2種非完美維修方式,即“兩級非完美”維修方式。圖1以部件i在第j-1次預防性維修時,分別采用初級維修和高級維修闡述兩級非完美維修方式的故障率演化規則。 由圖1可知,初級維修后部件的故障率高于上一次維修(無論初級或者高級)后部件的故障率,而高級維修后部件的故障率只高于上一次高級維修之后的故障率。 根據兩級非完美維修故障率演化規則,對部件采取不同的預防性維修方式,維修之后部件的故障率遞增速率和役齡遞減速率也不同。部件的役齡遞減因子和故障率遞增因子的表達式為 ( 2 ) ( 3 ) ( 4 ) 當部件到達預防性維修時刻時,部件有2種維修方式可供選擇。在此,以效費比作為具體維修方式的衡量標準。部件預防性維修前后的故障率分別為 ( 5 ) ( 6 ) ( 7 ) 進而式( 4 )可為 ( 8 ) 本文對動車組部件發生突發故障所導致的風險[12]主要考慮了3個方面:故障維修的難易程度;故障對動車組晚點的影響;故障對動車組運行安全性的影響[13]。 引入故障風險因子 ( 9 ) 式中:n為決定因素的個數;τi,k為對決定因素k的評分;αi,k為決定因素k的權重。 參照文獻[14-16]對設備重要度的評價方法,確定各決定因素的評分標準,見表1。 表1 各決定因素的評分標準 對于各決定因素權重的確定,采用層次分析法為[17-18] 首先,構造各決定因素間相對風險判斷矩陣M (10) 式中:umn為m相對于n的風險大小。 各決定因素之間相對風險的取值見表2。 表2 相對風險尺度及含義 然后,求解矩陣M的最大特征根ζmax,并代入方程組 (11) 求得ζmax對應的特征向量即為各決定因素的權重值。 最后,參照文獻[14]中的方法檢驗并校對M的一致性,直至M具有滿意的一致性。 綜上可得,部件的故障風險表達式為 (12) 式中:cu為單位故障風險成本。 在(0,lmax)內,部件的總成本包含預防性維修成本、故障維修成本和故障風險成本。 (1) 預防性維修成本 (13) (2) 故障維修成本 (14) 綜上可得,部件i在(0,lmax)內的維修總成本可表示為 (15) 通過求解minCp可得各部件的預防性維修計劃。此時,各部件之間的預防性維修計劃彼此獨立,不存在關聯性。 POM的基本原理是對某部件執行PM計劃時,對還未到達預防性維修時機的部件提前進行預防性維修。從某種意義上講,POM可能意味著生產設備的過維修或者維修資源的浪費,但也可降低設備的停機維修次數,提高生產設備的運營效率。對由M個部件組成的某機械系統,POM可以減少動車組的停機次數,從而降低固定維修成本和停機損失成本。 由圖2可知。對于部件i,存在 (16) 基于ΔL的系統層POM決策[19]步驟如下: Step1求解部件層minCp所對應的R值及其對應的預防性維修計劃。 Step2對ΔL進行賦值,取ΔL=2x,x為自然數。 (17) Step5確定li,j是否超出lmax,若li,j小于lmax,則轉入Step2進行下一周期的計算,直至所有部件的累積運行里程都超出lmax為止。此時,系統的POM總成本為 (18) 最后,通過比較ΔL在不同取值情況下的Cpo,選取最佳的ΔL作為機會維修里程窗,并得出系統層各部件的預防性機會維修計劃。 以故障率函數服從Weibull分布的動車組內某個由4個串聯部件組成的機械系統為例,進行分析 (19) 式中:m為形狀參數;η為生命特征參數。 對部件2的預防性維修計劃在取不同ψ值的情況進行分析。根據2.2節中部件故障風險的確定方法,求得部件2在不同情況下的ψ值。表3是部件2的預防性維修計劃在ψ取不同值情況下優化結果的對比;圖3是部件2的可靠度在ψ取不同值情況下的演化對比。 由表3可知,部件在一個壽命周期內的維修計劃對ψ的取值具有很高的敏感性。當ψ取值不同時,部件在其一個壽命周期內的預防性維修計劃也有較大的差異。例如:當ψ=0,在一個壽命周期內對部件只需要執行3次初級維修;而當ψ=5.09時,對部件執行了8次初級維修和2次高級維修。因此,在生產實際中,應根據部件故障后果的實際情況,對其故障風險因子進行賦值。 表3 不同ψ取值情況下PM優化結果對比 由圖3不難看出,考慮故障風險可以使部件在一個完整的壽命周期內保持更高的可靠度水平。并且ψ取值越高,部件在一個壽命周期內的可靠度水平越高,這說明對于故障風險高的部件,使其在壽命周期內保持較高的可靠度水平不僅符合安全性的要求,也符合維修經濟性的要求。 系統層POM的優化結果見表4,對應各部件的POM計劃示意見圖4。 由表4可知,系統層機會維修里程窗的優化結果為ΔL=4萬km,維修總成本為47 906元。由圖5可以看出,在一定的優化區間內,存在唯一ΔL值使得系統層維修總成本最低,所以選取合適的ΔL值對降低系統維修總成本具有重要的經濟價值。 表4 系統層POM優化結果 表5是在同等條件下POM與PM的維修總成本和維修次數的對比。分析表5可知,相比于PM,雖然POM對部件1、2、3各多執行了1次初級維修,但是POM的停機維修次數比PM減少了20次,使得POM的維修總成本(47 906元)比PM的維修總成本(63 093元)降低了24.1%。 表5 維修總成本和維修次數對比 部件POM PM neonsonepnspCpo/元nepnspCp/元1234854302100444200247 9067877221263 093停機次數1636 本文基于高速鐵路動車組運行速度快,故障危害大等特點,引入機會維修思想,建立了考慮故障風險的動車組部件機會維修優化模型。算例分析表明: (1) 考慮故障風險,有助于動車組部件在一個完整的壽命周期內保持更高的可靠度水平。對于故障風險較高的部件,應提高其預防性維修的頻率,并且在其壽命周期的后半階段,應適當采取高級別的維修措施,這與實際情況相符。 (2) ΔL的合理取值對降低多部件系統的維修總成本具有重要作用。ΔL取值太大容易造成過維修,浪費維修資源;ΔL取值太小則會造成系統停機頻繁,無法體現POM的優勢。 (3) 當ΔL=4萬km時,POM相比于PM的維修總成本下降了24.1%。因此,對于動車組這類停機損失大的系統,POM比PM具有顯著的經濟優越性。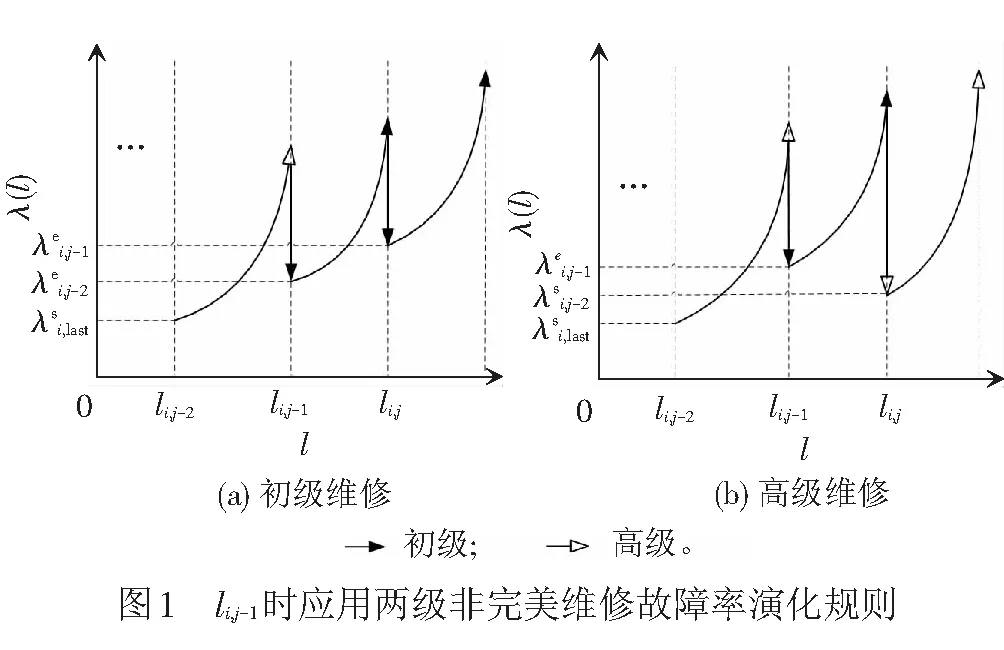

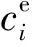
2.2 故障風險的確定
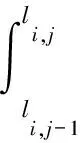
2.3 總成本建模
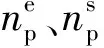
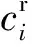
3 系統層預防性機會維修原理
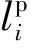
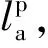
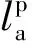
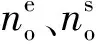
4 算例分析


5 結論

