物理模型及邊界條件對直流蒸發管兩相流不穩定性邊界影響研究

蘇 陽，李曉偉，閻慧杰，吳莘馨，梁 騫

(清華大學 核能與新能源技術研究院，先進核能技術協同創新中心， 先進反應堆工程與安全教育部重點實驗室，北京 100084)

高溫氣冷堆憑借其固有安全性及高溫工藝熱應用前景，具有很好的發展前途。螺旋管式直流蒸汽發生器作為高溫氣冷堆一、二回路的熱量傳輸樞紐，其安全運行至關重要。蒸汽發生器的兩相流不穩定現象會導致二回路流量、溫度和壓力脈動，不僅干擾控制系統，甚至還會導致傳熱管發生機械振動及熱疲勞而損壞。因此，研究和避免發生兩相流不穩定性是蒸汽發生器熱工水力設計及分析的重要內容。

Boure等[1]將兩相流動不穩定性分為兩類最基本的類型，即靜態不穩定性和動態不穩定性，其中動態不穩定性又分為密度波、壓力降和熱力型等。Lahey等[2]運用頻域法研究了沸水堆(BWR)中的密度波脈動，同時總結了前人關于單通道和并聯通道的研究結果。Ma等[3]運用時域法研究了流動方向上熱流密度均勻分布和熱流密度遞減分布對不穩定性邊界的影響，得到均勻分布比遞減分布更穩定。Hirayama等[4]運用集總參數法研究了自然循環并聯管道的兩相流不穩定性，觀察到并聯管道入口流量相位差為180°。馬越等[5]運用時域法對垂直上升管內兩相流不穩定性進行研究，建立了垂直上升直管內流動沸騰過程的一維模型，并編制計算程序，同時分析了密度波不穩定性發生的機理。

近年來，很多學者使用RELAP5程序來研究兩相流不穩定性。RELAP5運用有限差分法對一維瞬態控制方程組進行離散，通過數值求解離散方程組得到各參數隨時間的變化，屬于時域法。Ambrosini等[6]運用RELAP5計算不穩定性時，認為時間步長和空間節點的參數設置對平衡、均勻(EVET, equal velocity equal temperature)模型影響更大，且EVET模型計算結果過于保守。付文等[7]運用RELAP5程序模擬了垂直并聯直流蒸發管道的流動工況，得到的脈動特性和不穩定性邊界與實驗結果吻合很好。Marco等[8]運用RELAP5模擬了不同工況下的兩相流不穩定性邊界情況，發現不穩定性邊界無明顯區別。Xia等[9]運用RELAP5研究了恒定流量下2、4和9根并聯直流蒸發管的兩相流不穩定性，得到的流量脈動曲線無明顯區別。

雖然很多學者運用RELAP5計算不穩定性邊界，但對不同邊界條件及物理模型對不穩定性邊界的影響研究較少。本文模擬單根直流蒸發管和2根并聯直流蒸發管實驗，驗證RELAP5模型及計算方法，在此基礎上，研究恒定流量和恒定壓降兩種邊界條件下并聯管數量、軸向功率非均勻分布及熱容對不穩定性邊界的影響。

1 模型及計算方法驗證

首先根據王芊[10]和Takitani等[11]的實驗數據驗證RELAP5/MOD3.4計算直流蒸發管兩相流不穩定性邊界的可行性，其中王芊[10]的實驗為出口未過熱的單根直流蒸發管流動不穩定性，Takitani等[11]的實驗為出口過熱2根并聯直流蒸發管流動的不穩定性。

圖1示出實驗段的節點劃分。圖1中，202TMD控制入口過冷度，224TMD控制出口壓力，201SJ控制入口流量，207J和307J控制入口節流系數，209J和309J控制出口節流系數。并聯直流蒸發管在下腔室用206B連接，在上腔室用220B連接。200P和300P用來模擬加熱通道，使用電加熱的方式對其加熱。204S、222S、210S、310S、214S和314S為單一控制體，215J為單一接管。

Ambrosini等[6]認為非平衡、非均勻(UVUT, unequal velocity unequal temperature)模型和半隱式數值方法是最可靠的組合。因而，本文在預測直流蒸發管不穩定性邊界時也采用UVUT模型和半隱式數值方法的組合。

界限熱負荷隨網格數的變化如圖2所示。由圖2可見，網格數大于80后界限熱負荷變化很小，因此計算時網格數取為80。綜合考慮柯西準則和時間步長對數值結果的影響，取時間步長為10-3s。

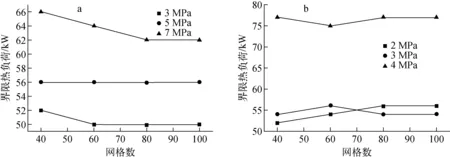
a——單根管；b——2根管圖2 界限熱負荷隨網格數的變化Fig.2 Boundary power variation with node number

在用RELAP5進行不穩定性邊界計算時，流量脈動幅值超過10%便認為該系統出現不穩定現象[12]。在確定不穩定性邊界時，采用逐漸增加功率的方法。當系統處于功率A下是穩定的，但增加到功率B下是不穩定的，為保守評估不穩定性邊界，便認為功率A是界限熱負荷[12]。根據Takitani等[11]的實驗幾何條件，以出口壓力為4.1 MPa、入口過冷度為104.83 ℃、進口質量流速為177 kg/(m2·s)、入口阻力系數為520、出口節流系數為5的工況為例具體說明不穩定性邊界的判定，圖3示出加熱功率變化時的流量脈動曲線。由圖3可知，在44 kW下，流量的振幅小于10%，系統處于穩定狀態。當功率上升到46 kW時，流量的振幅大于10%，系統處于不穩定狀態，可認為該工況下系統的界限熱負荷為44 kW。

圖3 出口流量隨功率的變化Fig.3 Oulet flow rate variation with power

根據王芊[10]的實驗工況，分別在3、5和7 MPa壓力下計算界限熱流密度，結果如圖4所示。由圖4可見，RELAP5計算與實驗界限熱流密度的相對誤差基本在40%以內，且是保守的。根據Takitani等[11]的實驗工況，按照上述的流程和標準，得到界限熱流密度如圖5所示。由圖5可見，RELAP5計算與實驗界限熱流密度相對誤差均在30%以內，且是保守的。

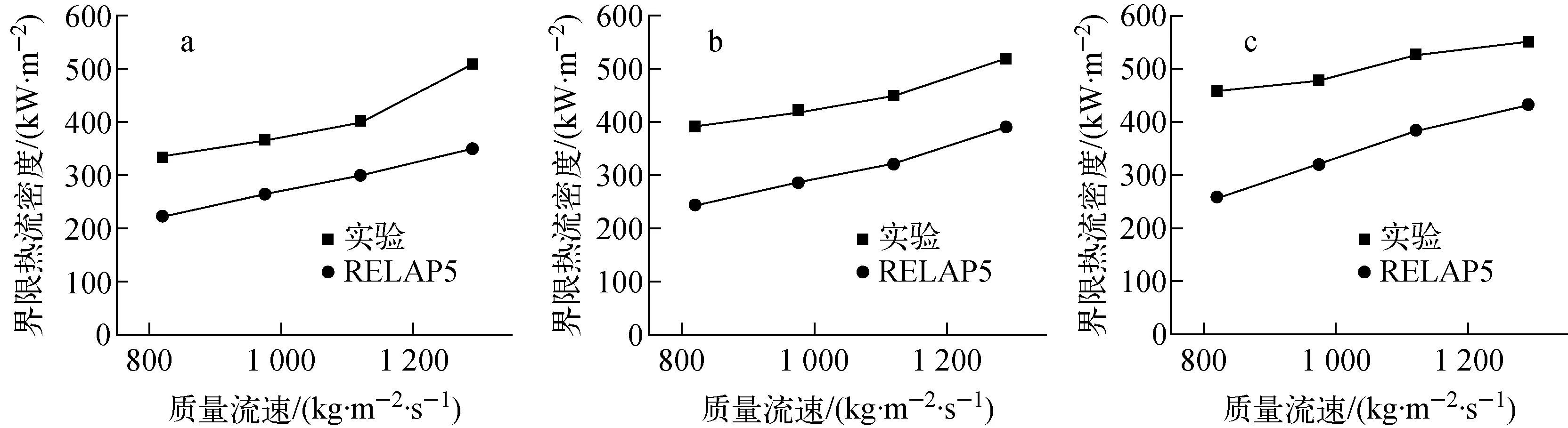
壓力：a——3 MPa；b——5 MPa；c——7 MPa圖4 單根直流蒸發管界限熱流密度對比Fig.4 Comparison of boundary heat flux of single once-through evaporation tube

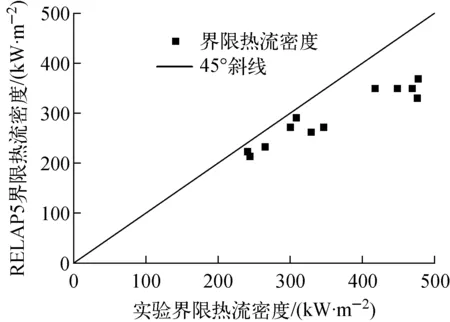
圖5 2根直流蒸發管界限熱流密度對比Fig.5 Comparison of boundary heat flux of two once-through evaporation tubes

2 并聯管數量及進出口邊界條件的影響

實驗條件下，由于驅動方式的不同，直流蒸發管進出口邊界條件介于恒定壓降與恒定流量之間。本文分別研究恒定流量與恒定壓降下，單根、2根、5根和8根并聯管對不穩定性邊界的影響。RELAP5算例的邊界條件及運行參數列于表1。算例的幾何模型與Takitani等[11]實驗的相同。

2.1 恒定壓降下并聯管數量對不穩定性邊界的影響

當邊界條件為恒定壓降時，需將圖1中的201SJ(TMDPJUN，控制入口流量)改成201J(SNGLJUN，只起連接作用)，此時202TMD控制入口過冷度和入口壓力，流量由進出口壓降決定。5根和8根管的計算，只需在圖1b的基礎上增加并聯管數量即可。

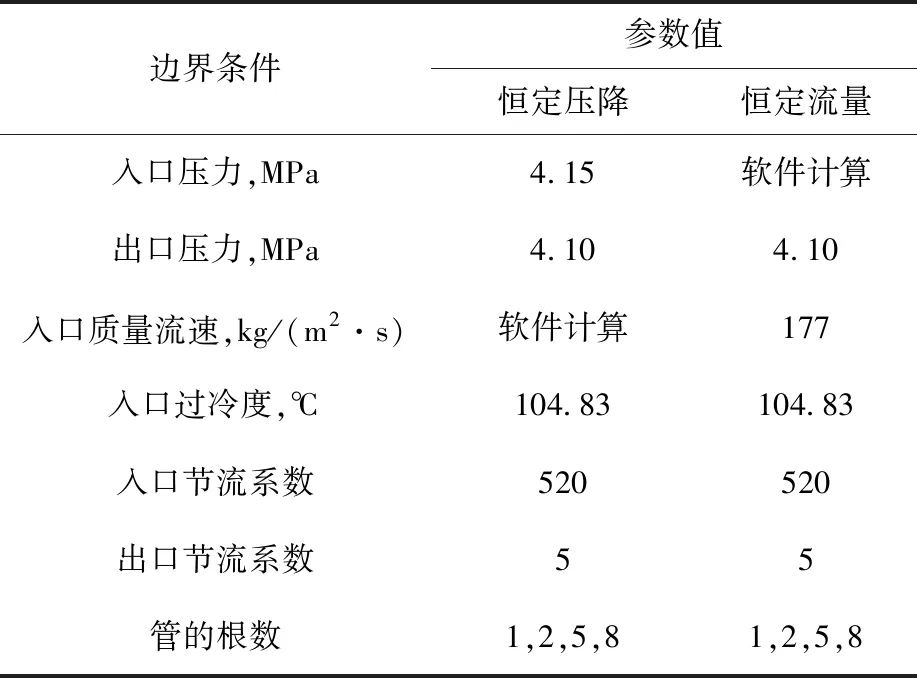
表1 算例的邊界條件和運行參數Table 1 Boundary condition and operating parameter of case

恒定壓降下并聯管數量對不穩定性邊界的影響如圖6所示。由圖6a可看出，在并聯管進出口壓力一定的條件下，單根和2根管的兩相流不穩定性邊界均為34 kW，且流量脈動曲線的波型、振幅和周期也幾乎相同。這說明進出口壓力一定的情況下，單根直流蒸發管可代替2根直流蒸發管進行不穩定性邊界的計算。由圖6b可看出，并聯管進出口壓力一定的條件下，5根和8根管的兩相流不穩定性邊界均為34 kW，且流量脈動曲線的波型、振幅和周期也幾乎相同。這說明恒定壓降邊界條件下，每根管的行為基本一致，不需各通道進行水力學聯系。

a——單根和2根管；b——2根、5根和8根管圖6 恒定壓降下并聯管數量對不穩定性邊界的影響Fig.6 Effect of number of parallel tube on instability boundary under constant pressure drop condition

2.2 恒定流量下并聯管數量對不穩定性邊界的影響

當邊界條件為恒定入口流量時，5根和8根管的計算只需在圖1b基礎上增加并聯管數量即可。

恒定流量下并聯管數量對不穩定性邊界的影響如圖7所示。由圖7a可看出，恒定流量情況下，直流蒸發管為單根時，功率達到90 kW時系統仍處于穩定。圖3顯示直流蒸發管數量為2根時不穩定性邊界為44 kW，這說明在恒定流量下單根和2根直流蒸發管的不穩定性邊界不相同，且差別較大。單根管時，如果進口流量恒定，則此時只會出現出口流量脈動。而恒定壓降邊界條件下，進出口均會產生脈動，因而更易發生密度波不穩定性。

從圖7b可看出，并聯管數量為5根或8根時，界限熱負荷為42 kW，并聯管數量為2根時，界限熱負荷為44 kW。因此，并聯管數量為2根、5根或8根時，不穩定性邊界幾乎無區別，在恒定流量下2根管可代替多根管進行不穩定性邊界的計算。

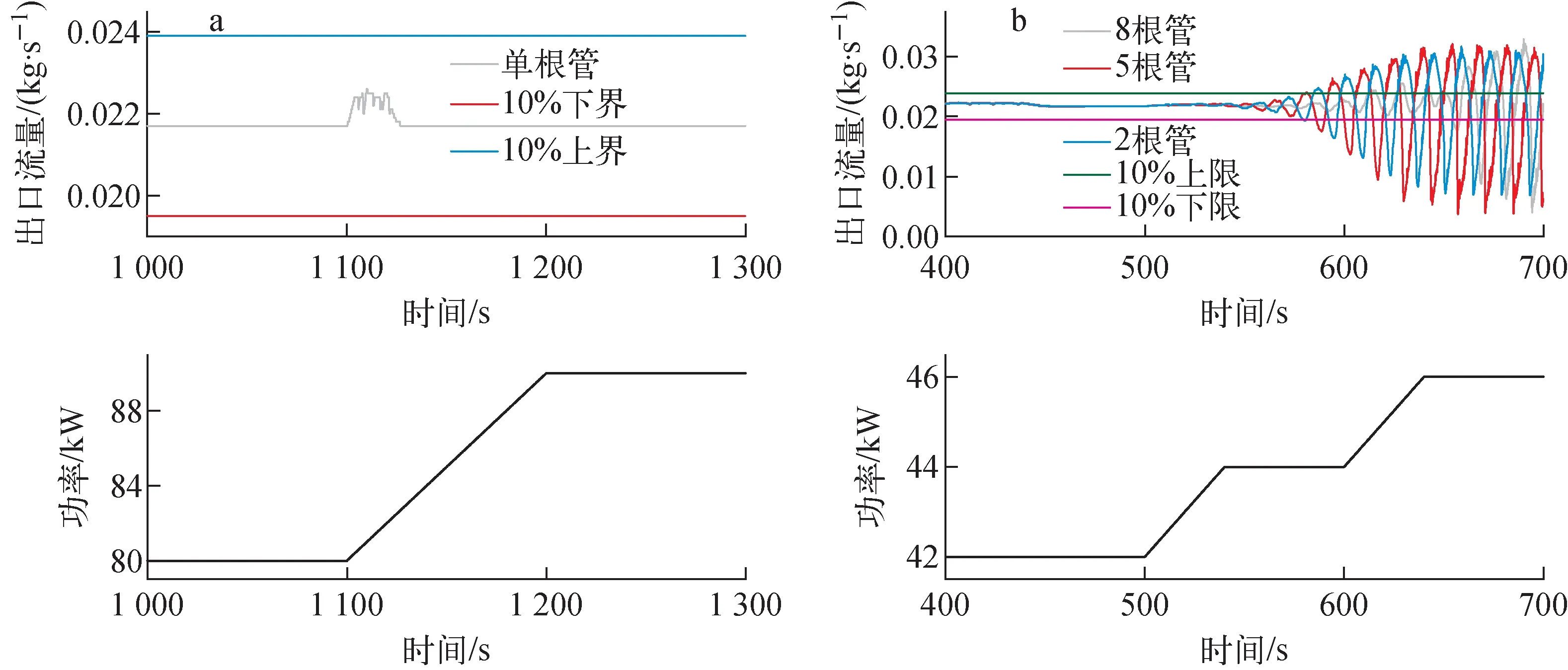
a——單根管；b——2根、5根和8根管圖7 恒定流量下并聯管數量對不穩定性邊界的影響Fig.7 Effect of number of parallel tube on instability boundary under constant flow rate condition

2.3 相同并聯管數量下進出口邊界條件對不穩定性邊界的影響

恒定壓降邊界條件下，單根、2根、5根和8根管的界限熱負荷均為34 kW；恒定流量邊界條件下，單根管的界限熱負荷大于90 kW，2根管的界限熱負荷為44 kW，5根和8根管的界限熱負荷為42 kW。因而可知，并聯管數量相同時，恒定流量邊界條件的穩定性好于恒定壓降邊界條件。單根管時，如果進口流量恒定，則此時只會出現出口流量脈動。而恒定壓降邊界條件下，進出口均會產生脈動，因而更易發生密度波不穩定性。2根及多根管時，恒定壓降邊界條件下，每根管的行為基本一致，不需各通道進行水力學聯系，因而更易發生密度波不穩定性。

綜上可見：當進行兩相流不穩定性邊界計算時，恒定壓降邊界下單根管便可代替多根管進行不穩定性邊界的計算；恒定流量邊界條件下，2根管可代替多根管進行不穩定性邊界的計算；并聯管數量相同時，恒定流量邊界條件的穩定性好于恒定壓降邊界條件。在實際情況下，進出口邊界條件一般介于恒定流量和恒定壓降兩者之間。因而，在分析多根管系統時，考慮到恒定壓降邊界條件不穩定性邊界過于保守，可運用2根并聯直流蒸發管結合恒定流量邊界條件分析系統的不穩定性邊界。

3 軸向功率分布和管壁熱容的影響

在一些實驗中，往往采用電加熱方式對直流蒸發管加熱，其軸向熱流密度是均勻分布的。而實際蒸發器大多是對流加熱形式，對流加熱形式使熱流密度非均勻分布。如高溫氣冷堆螺旋管式蒸汽發生器，由于二次側出口處氦氣-水蒸氣溫差大，二次側入口處氦氣-水溫差小，所以其過熱蒸汽段熱流密度最大，蒸發段其次，而預熱段熱流密度最小。因此需分析軸向功率密度分布對不穩定性邊界的影響。另外，有些分析方法對兩相流不穩定性進行分析時不能考慮管壁熱容，而管壁熱容會影響瞬態的熱流密度，因此也有必要分析管壁熱容對不穩定性邊界預測準確性的影響。

3.1 軸向功率分布的影響

采用3種軸向功率分布形式來研究軸向功率分布對不穩定性邊界的影響，如圖8所示。圖8中，up指沿流動方向上功率線性增加，uniform指沿流動方向上功率均勻分布，down指沿流動方向上功率線性減小。

圖8 3種軸向功率分布形式Fig.8 Three axial power distribution patterns

軸向功率遞增和遞減分布下的不穩定性邊界如圖9所示。由圖9a可看出，軸向功率遞增分布下，在80 kW下未發生脈動，界限熱負荷大于80 kW。由圖9b可看出，軸向功率遞減分布下，系統的界限熱負荷為30 kW。由圖3可知，軸向功率均勻分布下，界限熱負荷為44 kW。在其他條件一致的情況下，系統穩定性趨勢為：沿流向功率遞增分布穩定性好于沿流向功率均勻分布，沿流向功率均勻分布穩定性又好于沿流向功率遞減分布。其原因為當入口功率較小時，單相液區較長，有利于系統的穩定；而入口功率較大時，兩相區及過熱區較長，不利于系統的穩定。

3.2 管壁熱容的影響

在工業應用中，傳熱管壁厚一般小于10 mm，因而在0～20 mm厚度范圍內分析傳熱管壁熱容對不穩定性邊界的影響。

分別取壁厚為0.05、1.25、3、5、8、10、12和20 mm，得到的界限熱負荷如圖10所示。在管壁逐漸變厚過程中，即熱容不斷增大，界限熱負荷先稍微增加然后減小最后趨于穩定，但變化的范圍很小。因而可認為管壁熱容對不穩定性邊界幾乎沒有影響。管壁熱容會吸收一部分脈動，起到穩定系統的作用。

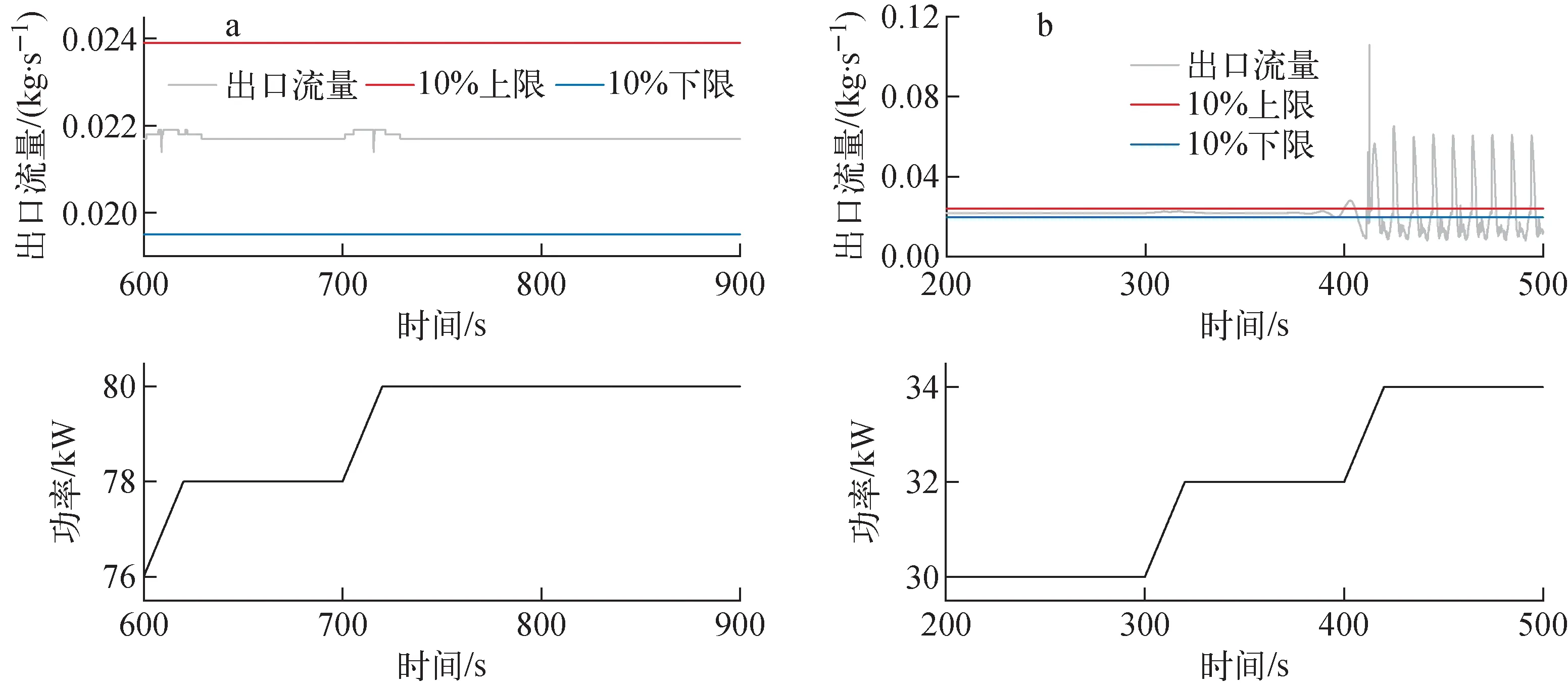
圖9 軸向功率遞增(a)和遞減(b)分布下的不穩定性邊界Fig.9 Instability boundary under increasing (a) and decreasing (b) axial power distribution conditions

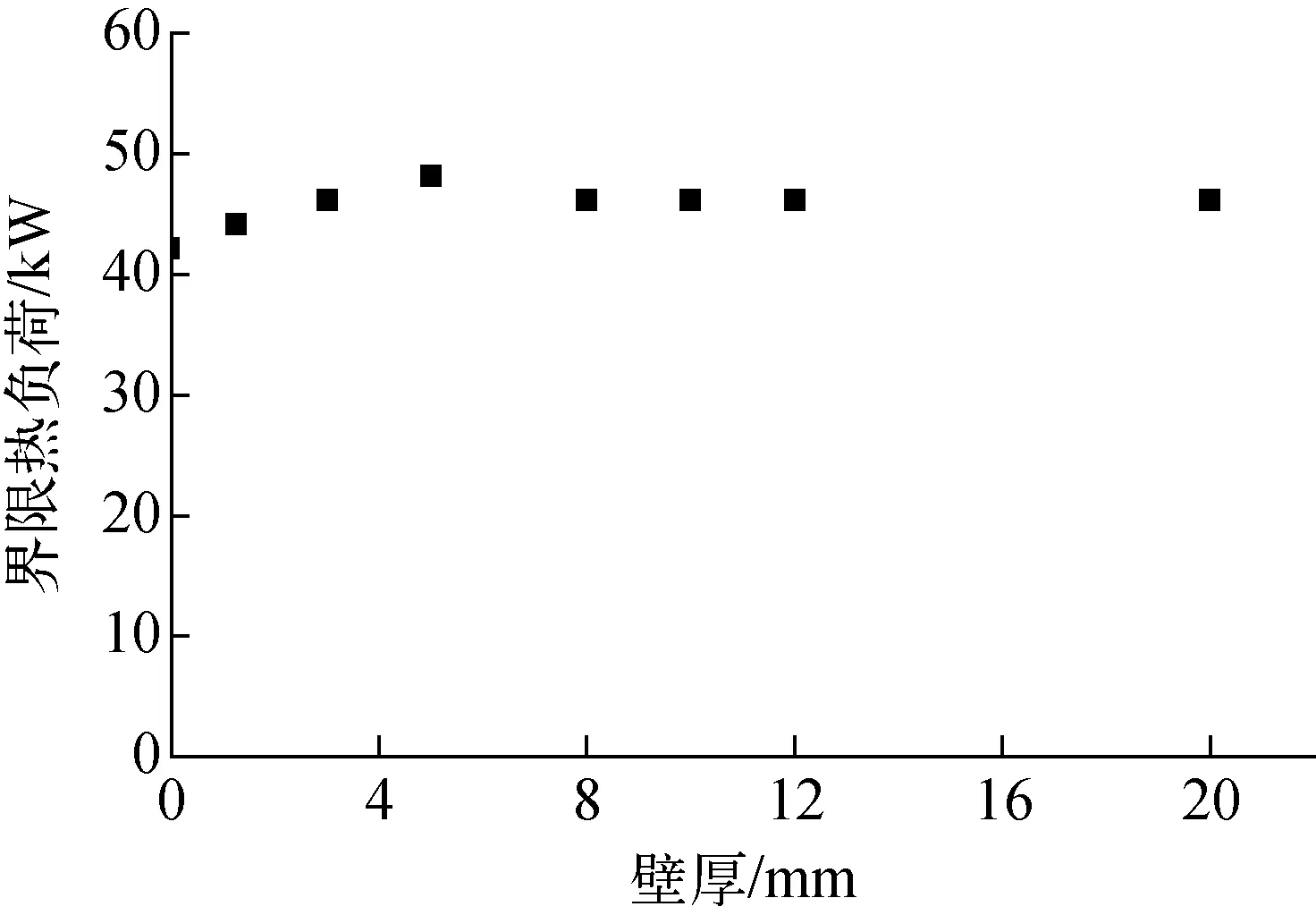
圖10 不同壁厚下的不穩定性邊界Fig.10 Instability boundary with different tube wall thicknesses

4 結論

采用RELAP5研究了進出口邊界條件、并聯管數量、軸向功率分布形式及傳熱管壁熱容等不同物理模型及邊界條件對直流蒸發管兩相流不穩定性邊界的影響，得到的主要結論如下。

1) 當進出口邊界條件為恒定壓降時，單根、2根和多根直流蒸發管的不穩定性邊界無明顯差別。當進口邊界條件為恒定流量時，單根直流蒸發管系統較2根和多根的穩定性好，而2根和多根系統不穩定性邊界基本相同。并聯管根數相同時，恒定流量邊界條件的穩定性好于恒定壓降邊界條件。因此，在分析多根管系統時，可保守地運用2根并聯直流蒸發管結合恒定流量邊界條件分析系統的不穩定性邊界。

2) 軸向功率分布形式對不穩定性邊界的影響較大，在其他條件相同的情況下，沿流向功率遞增分布穩定性好于沿流向功率均勻分布，沿流向功率均勻分布穩定性又好于沿流向功率遞減分布。

3) 在一般傳熱管壁厚(0～20 mm)條件下，傳熱管壁熱容對直流蒸發管兩相流不穩定性邊界基本沒有影響。