一種基于等效源法的表面阻抗現場測量方法
李曷冰,胡定玉,劉馨悅,方 宇
(上海工程技術大學 城市軌道交通學院,上海201620)
材料的表面阻抗能夠反映材料的聲學性質,是材料的重要聲學參數之一。在室內噪聲控制、戶外環境噪聲的治理、汽車車內噪聲控制等領域具有廣泛的應用。準確測量吸聲材料的表面阻抗,具有重要的工程意義。
常用的表面阻抗測量方法有傳遞函數測量法[1]和駐波比法[2–3],這些方法需要在阻抗管中進行測量,并不能測得材料在現場實際條件下的吸聲性能,此外測量時需要將材料切割成特定的小塊,通常會對材料造成損傷[4]。采用近場聲全息技術進行阻抗測量可以彌補這些不足,Tamura[5–6]使用空間二維傅里葉變換法來測量材料的阻抗,通過采集平行于待測材料表面的兩個平行面上的聲壓值,計算其反射系數,利用反射系數與材料表面阻抗之間的關系間接計算阻抗值,國內聶佳[7]等采用主動聲源進行全息計算,對該方法進行了進一步研究;Zhang[8]采用等效源法進行表面阻抗測量,該方法通過采集平行于材料表面上方兩條平行線上的聲壓值,利用基于等效源法的近場聲全息技術計算聲壓和質點振速,直接得到阻抗值。這兩種方法不需要將材料切割成特定的小塊,但仍需要在消聲室環境內進行測量。除此之外,Nava[9]采用邊界元法來測量材料的表面阻抗,雖然不需要在消聲室環境內進行測量,但要求測量面覆蓋整個內空間表面,同時該方法在計算過程中使用了大量的插值運算,導致其計算效率較低。
一般在現場測量環境中,不僅有入射聲和反射聲,傳感器陣列未能覆蓋到的區域還會有背側干擾聲。針對這種現場環境,本文提出一種基于等效源法[10]的材料表面阻抗測量方法,通過構造虛擬腔體,來充分考慮測量面各個方向上的聲信號,最終對材料表面阻抗進行全息計算。本文以數值仿真的形式,對該測量方法的有效性以及該方法對復雜測量環境的適應能力進行分析驗證,最后對主動聲源以及等效源的位置等參數進行分析并給出建議。
1 理論基礎
1.1 基于等效源法的近場聲全息原理
等效源法的原理是[11]布置一系列的簡單源(即等效源)來擬合實際聲場,通過確定所有等效源的源強實現聲場的重建。如圖1所示。

圖1 等效源法基本原理圖
要重建腔體內部的聲場,可在腔體外部布置等效源,則腔體內部任一點r處的聲壓可表示為[12]
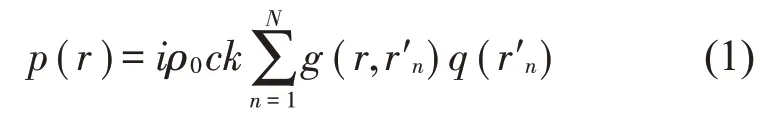
式中:i 為虛數單位,ρ0為空氣密度,c 為聲速,k 為波數,q(r′n)為r′n處的等效源源強,N 表示所布置的等效源個數,g(r,r′n)為自由聲場格林函數
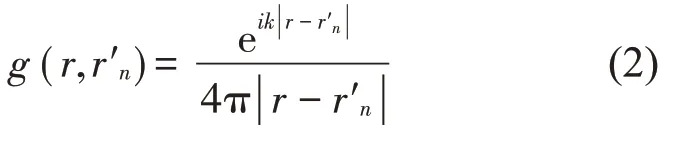
當測量面上有M 個測點時,測量面上的聲壓以矩陣形式表示為

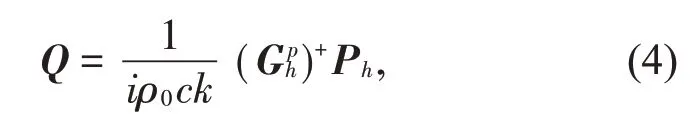
式中:“+”代表求解矩陣的廣義逆。
由于重建聲場時涉及聲波反向傳播的問題,因此,在式(1)求解廣義逆的過程中,需要采用正則化方法[13]來穩定求解。本文采用的是Tikhonov正則化法,并通過L 曲線法[14]選取正則化參數。利用式(4)進一步求出材料表面的聲壓和質點振速為
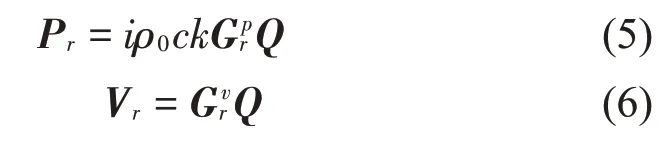
1.2 基于等效源法的表面阻抗測量方法基本原理
本文提出的材料表面阻抗的測量方法原理如圖2所示。
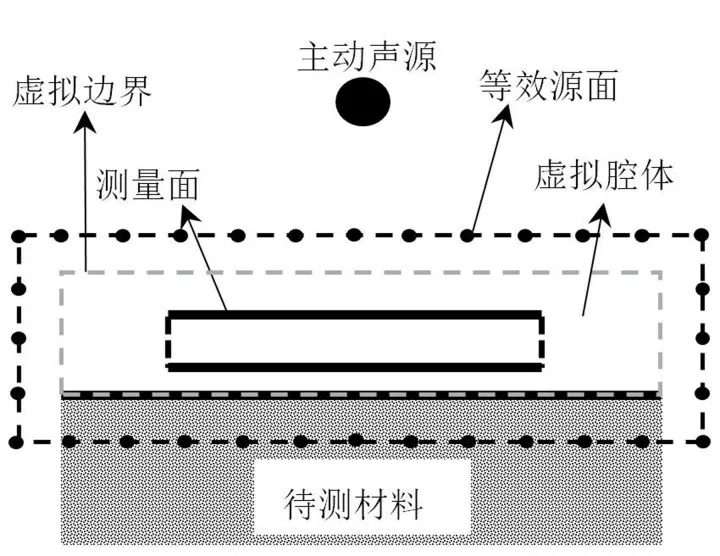
圖2 基于等效源法的表面阻抗測量方法基本原理圖
首先在材料表面上方布置一個主動聲源,然后在主動聲源和待測材料中間區域定義一個虛擬腔體,在腔體內部用封閉測量面采集聲壓。利用基于等效源法的近場聲全息技術,計算出虛擬腔體邊界處的聲壓和質點振速。通過式(1)至式(6)求得材料表面任意一點r 處的聲壓和振速,從而獲得表面阻抗為
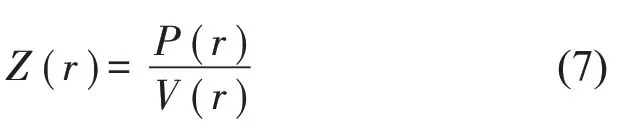
從本文方法原理可以看出,該方法可在現場測量環境下使用,且測量面不需要覆蓋整個內空間表面,僅對自己感興趣的區域進行測量即可。
2 數值仿真
如圖3 所示,主動聲源置于材料表面上方(0,0,0.3 m)處,干擾聲源位于材料表面上方(-0.35 m,0.35 m,0.25 m)處。在等效源面內定義一個封閉的虛擬腔體并在其內部采集聲壓,測量面由兩個距離很近的正方形平面構成,邊長均為0.35 m,與待測材料之間的距離分別為0.03 m 和0.01 m,其上共有98個測點,間隔為0.05 m,由于2 個測量面距離很近,因此可以視作是一個封閉的測量面。210 個等效源分布在邊長(0.39′0.39′0.16)m3的立方體面上,相鄰間隔為0.05 m。仿真時加入信噪比為30 dB 的高斯白噪聲。
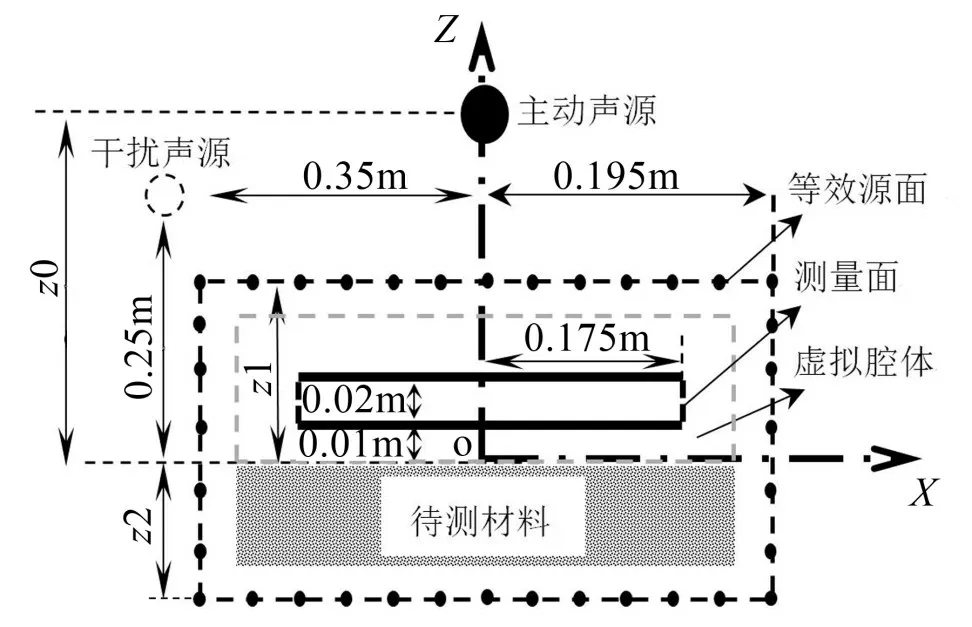
圖3 測量模型示意圖
為了定量地評價本文方法,定義計算誤差為
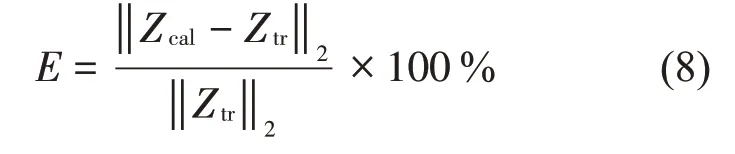
式中:Zcal為材料表面上49 個點處的表面阻抗平均值,Ztr為真實的表面阻抗值。
待測材料為纖維狀吸聲材料,假設材料的厚度為無限大,則其特征阻抗為[15]

式中:σ(流阻率)=50 cgs,Z0=ρ0c 表示空氣的特征阻抗。
2.1 方法有效性驗證
仿真中分別以單極子和偶極子為主動聲源,驗證本文方法的有效性。圖4(a)和圖4(b)分別給出了材料表面阻抗實部與虛部的測量值,可以看出在500 Hz~4 000 Hz 頻率范圍內,表面阻抗的測量值與理論值吻合較好。
圖5給出了采用單極子和偶極子作為主動聲源時的測量誤差,可看出,在500 Hz~4 000 Hz頻率范圍內其誤差都在10%以內。證明了本文方法對兩種不同類型聲源的有效性。
2.2 測量環境的適應能力分析
仿真中以偶極子作為主動聲源,同時在待測材料上方布置一個偶極子作為干擾聲源,其它參數與2.1小節一致。
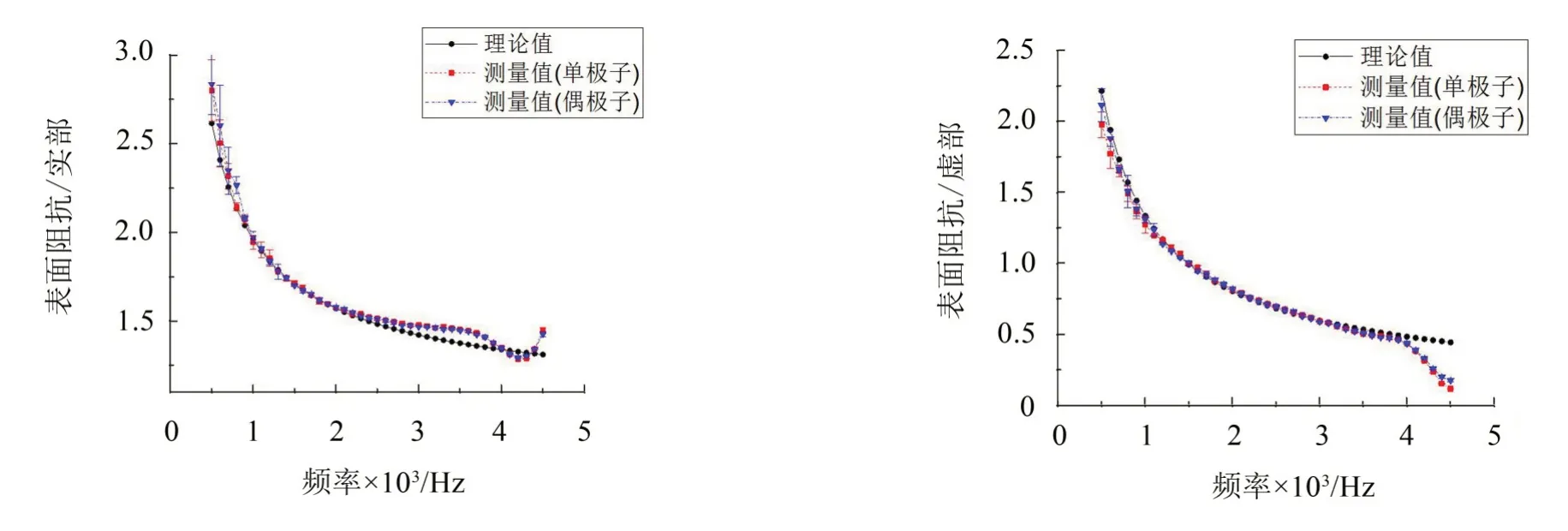
圖4 表面阻抗測量值與理論值的比較
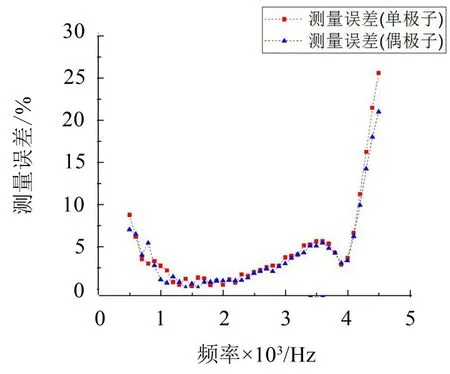
圖5 測量誤差曲線圖
圖6給出了本文方法測量值與理論值的比較結果,從圖中可看出,在500 Hz~4 000 Hz 頻率范圍內,本文方法得到的實部和虛部都與理論值吻合較好。圖7給出了測量誤差曲線,可看出,在500 Hz~4 000 Hz內,誤差依然在10%以內,證明了本文方法對復雜測量環境有較好的適應能力。
2.3 主動聲源位置分析
保持2.2小節中的仿真設置不變,改變主動聲源位置(如圖3 所示)z0,來分析其對測量誤差的影響。圖8給出了500 Hz、1 000 Hz和2 000 Hz頻率下不同位置處的測量誤差。可看出,在0.2 m~0.4 m 范圍內誤差最小。因此,建議將主動聲源放置于材料表面上方0.2 m~0.4 m處。
2.4 等效源位置分析
保持2.2小節中的仿真設置不變,改變等效源面上下表面的位置(如圖3所示)z1和z2,來分析其對阻抗測誤差的影響。圖9 給出了500 Hz、1 000 Hz 和2 000 Hz 3個頻率的分析結果。
可看出,當等效源面上下表面距材料表面0.075 m~0.175 m 時測量誤差最小。因此,建議等效源面上下表面到材料表面距離為0.075 m~0.175 m,且關于材料表面對稱。

圖6 存在干擾條件下表面阻抗測量值
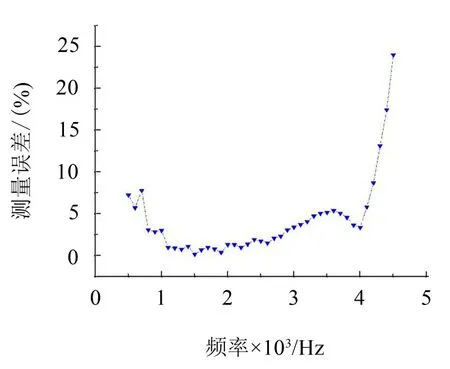
圖7 存在干擾條件下表面阻抗測量誤差曲線圖
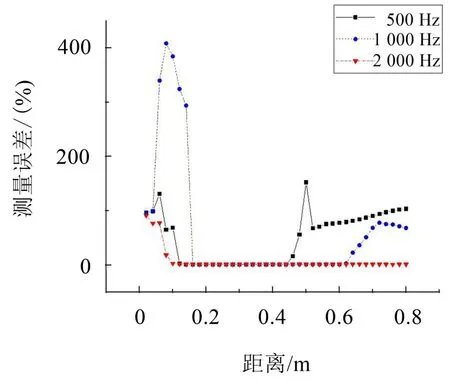
圖8 聲源位置對精度的影響
3 結語
本文提出了一種基于等效源法的材料表面阻抗測量方法,通過引入虛擬腔體,將問題轉換成近場聲全息的內部問題,實現了復雜環境下對材料表面阻抗的測量,且該方法只需要對感興趣的部分單獨測量。分別采用單極子和偶極子聲源模型作為主動聲源,并在測量環境中加入干擾聲源進行數值仿真,結果表明,在500 Hz~4 000 Hz內,本文方法能準確獲取表面阻抗,且對測量環境具有良好的適應能力。通過分析主動聲源以及等效源位置對測量誤差的影響,得出主動聲源的最優位置為材料表面上方0.2 m~0.4 m處;等效源面上下表面最優位置為距材料表面0.075 m~0.175 m處,且關于材料表面對稱。
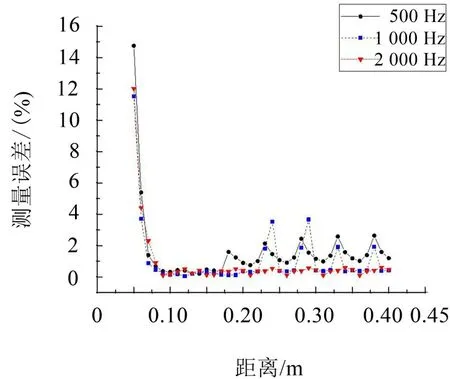
圖9 測量誤差隨等效源位置的變化圖

