庫水位漲落和降雨入滲對岸坡浸潤線的影響分析

張澤東

（新疆吉木薩爾城鎮水管所，新疆 吉木薩爾 831700）

庫水位漲落和降雨入滲是影響水庫庫岸邊坡穩定并引起岸坡滑坡的重要原因，統計資料顯示，日本大約有65%的水庫滑坡出現在庫水位驟降期間，其余35%則發生在庫水位上升時期，而《中國典型滑坡》中所列舉的水庫滑坡案例至少有90%與庫水位漲落和降雨密切相關，可見，研究庫水位漲落、降雨以及庫水位漲落和降雨聯合作用對庫岸浸潤線的影響，進而研究水庫岸坡浸潤線位置對滑坡穩定性的影響對于岸坡穩定性意義重大。近年來，國內外大量學者運用數值方法進行了地下水浸潤線的研究，如吳越，陸新等基于有限差分法進行了庫水位漲落和降雨入滲聯合作用的工況下滑坡過程中地下水位的計算[1]；林志紅，項偉等運用飽和滲流模型和非飽和滲流模型進行了庫水位漲落對浸潤線變化可能影響情況的模擬，并對降雨入滲機制進行深入探討[2]，然而數值方法原理復雜，僅適用于理論研究，在工程實際中運用較少。為此，筆者采用均質岸坡地質模型，充分考慮庫水位漲落、降雨入滲以及庫水位漲落和降雨入滲聯合作用，進行庫岸岸坡浸潤線的非穩定滲流計算，并據此對岸坡浸潤線變動規律進行分析。

1 岸坡浸潤線計算模型

1.1 假設條件

含水層具有均質性和各向同性，無側向延展性，底部主要是水平向非透水層，潛水流則表現為一維流態勢，庫水位漲落前庫岸岸坡初始浸潤線為H(x,0)；庫水位漲落范圍內垂直庫岸較小，則一維非穩定滲流方程為：

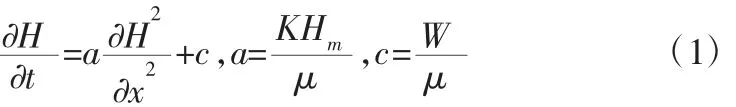
式中：α 為壓力傳導系數值，m2/d；Hm為含水層厚度均值，m；μ為重力給水度；K 為滲透系數，m/d；W 為降水入滲強度，m/d；c為降水有效強度，m/d；t 為降水持續時間，d。

1.2 岸坡浸潤線計算模型

在初始時刻t=0 時，庫岸岸坡初始浸潤線為H(x,0)，與庫岸相距x 處的地下水位變幅為S(x,t)，則t 時刻浸潤線方程表示如下：

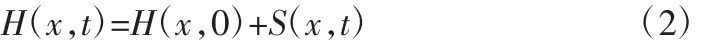
對于庫水位漲落與降雨入滲的聯合作用，地下水非穩定滲流模型表示如下：

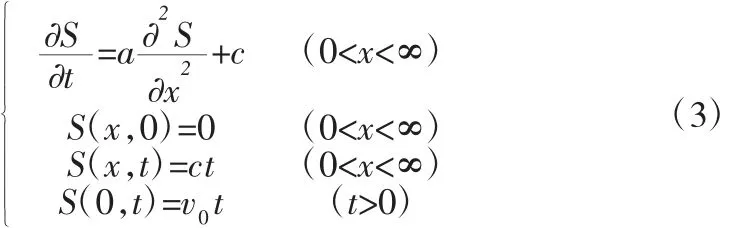
1.3 浸潤線方程求解

將方程組（3）進行拉普拉斯正逆變換求解，得：

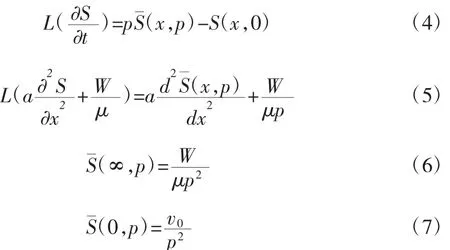
根據式（4）和（5）可知：

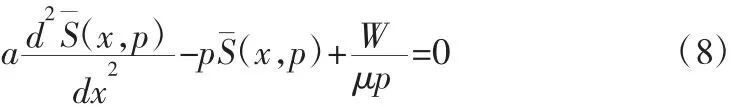
求得二階線性齊次微分方程（8）的通解如下：

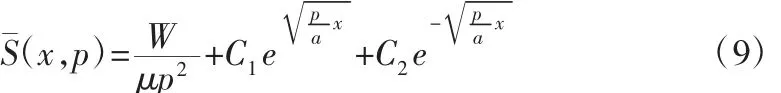
將式（6）和（7）代入式（9）可得：

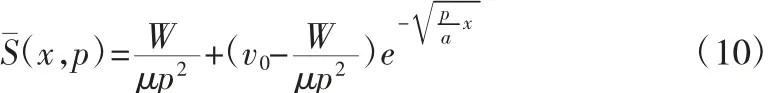
運用拉氏逆變換進行式（10）的化簡，得：

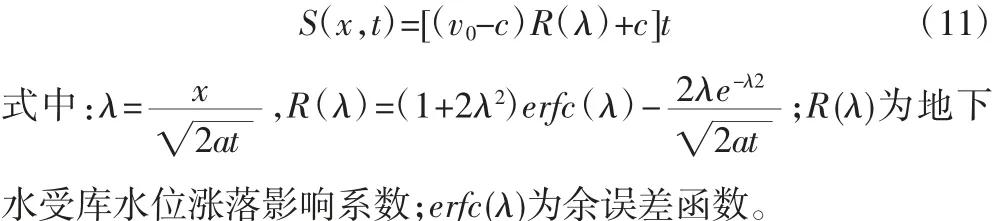
通過式（2）和（11）可以得到時刻t 庫水位漲落和降雨聯合作用下庫岸岸坡浸潤線方程[3]，即：

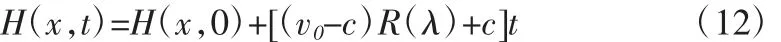
2 算例及分析

2.1 工程概況

東大龍口水庫座落于吉木薩爾縣吉木薩爾鎮東大龍口河流的中下游，是一座以防洪、農業灌溉、城市居民供水為主的中型水庫。東大龍口水庫規模為中型，水庫總庫容1250 萬m3。大壩壩型為粘土心墻土石壩，壩頂長度698 m，最大壩高35.5 m，壩頂寬5 m，壩頂高程(黃海)981.5 m。

為進行庫水位漲落和降雨入滲對岸坡浸潤線影響的分析，筆者結合東大龍口水庫工程實際，設計庫水位漲落范圍為145 m～175 m，落差30 m，分析模型見圖2。具體計算時采用MATLAB 分析工具繪制各種工況下岸坡浸潤線的分布情況[4]。

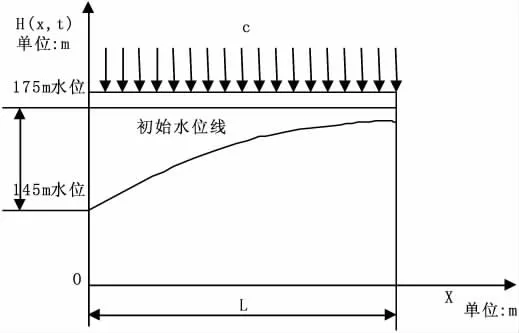
圖1 東大龍口水庫工程浸潤線計算模型

2.2 壓力傳導系數對岸坡浸潤線的影響

在圖1 計算模型中取L=100 m，求壓力傳導系數α 和下降時間不同且庫水位均勻下降情況下岸坡浸潤線的變動規律。由于東大龍口水庫水位調度方案中水位降速最大值為2.5 m/d，故計算時假設降速v0=2.5 m/d，得到岸坡浸潤線變動規律，見圖2、圖3。結合東大龍口水庫工程實際，相同斷面的岸坡水頭、水力梯度與壓力傳導系數α 呈相反變動，考慮到庫水位的作用，水力梯度呈動態變動趨勢，由圖2 可知，壓力傳導系數α隨著庫水位勻速下降而減小，浸潤線隨庫水位勻速下降而變得更加陡峭。

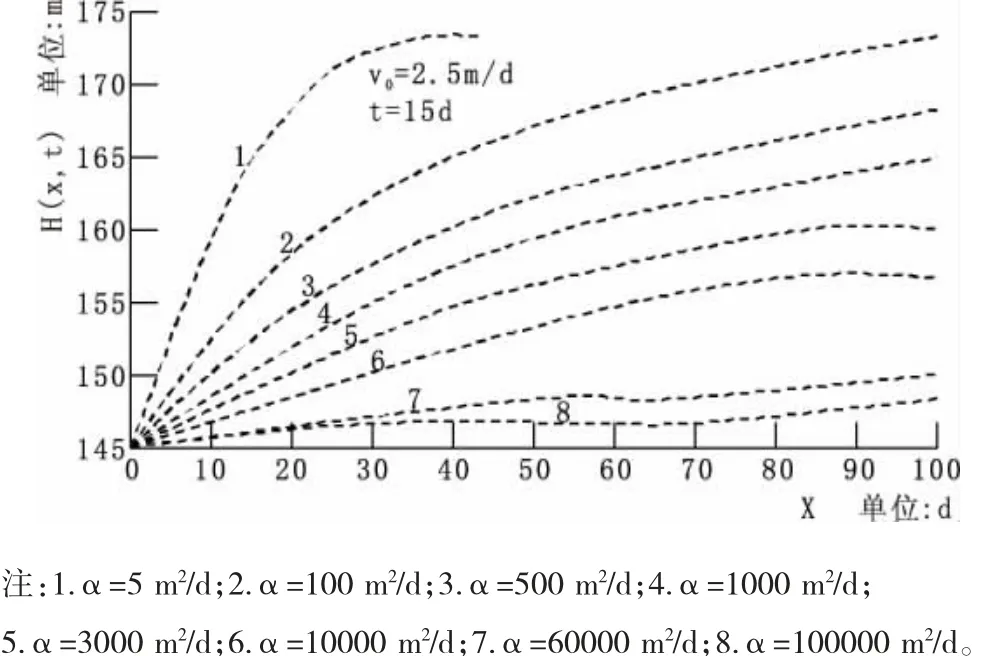
圖2 壓力傳導系數與浸潤線關系示意圖

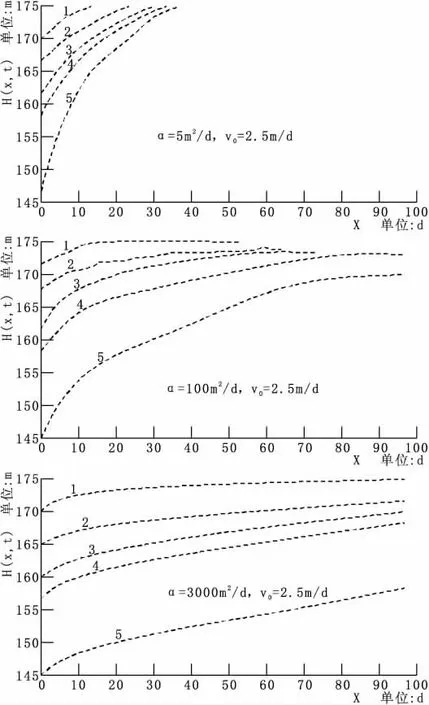
圖3 壓力傳導系數α 不同且庫水位均勻下降岸坡浸潤線的變動規律

從圖3 可以看出，在庫水位勻降的過程中，岸坡浸潤線的位置和形狀變化與壓力傳導系數α 取值大小有關，當α＜5 m2/d時，岸坡浸潤線與原來位置相比并無明顯變化，而且此種情況下，水力梯度與滲透力均較大，對岸坡穩定最為不利；當5 m2/d＜α＜3000 m2/d，岸坡浸潤線呈上凸形狀，水利梯度與滲透力逐漸減小；當3000 m2/d＜α＜4000 m2/d 時，岸坡水位與庫水位同時下降，浸潤線近似于傾斜的直線，變化緩和，斷面水力梯度達到很小；當α＞4000 m2/d 時，浸潤線為水平直線，岸坡滲透力趨于零，此時已無滲流穩定性計算的必要。

2.3 庫水位漲落速度對岸坡浸潤線的影響

在圖1 計算模型中取L=100 m，壓力傳導系數α=4000 m2/d，t=10 d，庫水位漲落速度 v0分別為0.1 m/d、0.5 m/d、1.0 m/d、1.5 m/d、2.5 m/d 和3.5 m/d 時浸潤線變化趨勢見圖4。岸坡斷面浸潤線呈非穩定變化趨勢，即相同時刻t，斷面水位變幅隨v0的增大而增大，浸潤線也更加陡峭；當v0＜0.5 m/d 時，浸潤線較為緩和，且與庫水位保持平行；而當v0=2.5 m/d 時，浸潤線滯后于庫水位，且水位差將達到5 m 高度。總之，隨著庫水位漲落速度v0的增大，岸坡浸潤線變幅與水力梯度均呈增大趨勢。

2.4 降雨入滲對岸坡浸潤線的影響

在圖1 計算模型中取L=100 m，壓力傳導系數α=4000 m2/d，有效降雨強度c 分別取0.5 m/d 和0.06 m/d，則降雨量相同的情況下，降雨持續時間為10 d（降雨強度c=0.5 m/d）的連續降雨比50 d（c=0.06 m/d）的連續降雨對岸坡浸潤線的影響更為明顯，兩種情況下的水位差分別為2.21 m 和1.32 m。所以在相同降雨量情況下，岸坡浸潤線的變動隨有效降雨強度的增大而增大，且越不利于岸坡穩定。

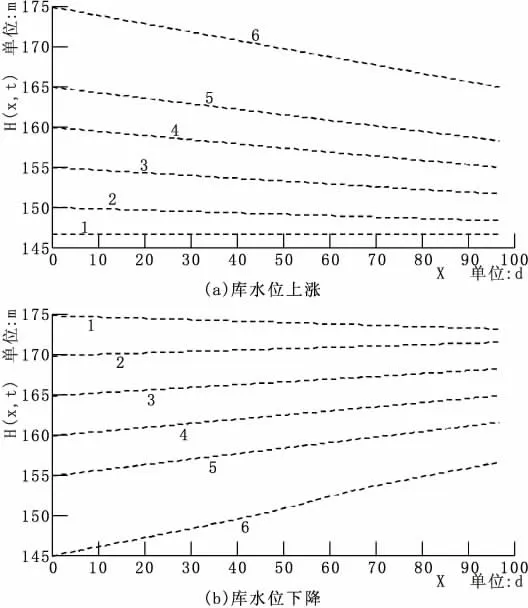
圖4 庫水位漲落時浸潤線變化趨勢

2.5 庫水位漲落和降雨入滲聯合作用對岸坡浸潤線的影響

在圖1 計算模型中取L=100 m，壓力傳導系數α=4000 m2/d，庫水位漲落速度0.5 m/d，有效降雨強度c 分別取0.1 m/d、0.2 m/d、0.3 m/d、0.5 m/d 和 1 .0 m/d，t=30 d，則根據庫水位勻速漲落和降雨入滲聯合作用時岸坡浸潤線的變動趨勢，庫水位由145 m 開始上漲，當有效降雨強度c 恰好等于庫水位漲速，則浸潤線平行于庫水位，此時水力梯度趨于零；而當有效降雨強度c 大于庫水位漲速，則隨x 的增大，岸坡地下水位隨之增大，并呈現上凸態勢；當有效降雨強度c 小于庫水位漲速，則隨x的增大，岸坡地下水位反而下降，并呈現下凹態勢。庫水位由175 m 開始下降時，岸坡浸潤線呈陡峭上凸態勢。

3 結論

文章從滲流基本原理出發，以非穩定滲流方程及邊界條件為依據，進行了庫水位勻速漲落和降雨入滲聯合作用下浸潤線變動規律的計算與分析，并推導出庫水位漲落與降雨入滲作用下浸潤線的近似解，計算過程中主要以穩定滲流狀態下的浸潤線作為非穩定滲流情況的初始值，使所求得的浸潤線結果更加合理。計算結果同時表明，岸坡浸潤線的位置與形狀與壓力傳導系數α 的大小有關，在相同的降雨量情況下，有效降雨強度越大則岸坡浸潤線變幅越大，越不利于岸坡穩定。