P2混動汽車傳動系統的數學建模方法

劉劍 黃良宇

廣州汽車集團股份有限公司汽車工程研究院 廣東 廣州 511400

前言

由于社會和政治的需要，混合動力汽車在過去十年間受到了極大的關注。一方面是由于氣候的不斷變化：根據歐盟2012年的數據，其22.4%的CO2排放來自于交通工具的排放；另一方面則是由于石油資源的限制和政治等因素導致燃油價格不斷上漲，因此對于更高效的低油耗汽車的需求越來越大。僅通過進一步發展車輛本身以及發動機技術，如減少摩擦損耗和結構輕量化等，無法滿足嚴格的排放限制，因此新型的混合動力汽車是一個很有前景的選擇[1-2]。

混合動力汽車包括一系列電氣部件以及機械部件，其動力總成的控制非常復雜，這些控制通常都是非線性的，建立仿真數學模型有利于提前對此類車型的研發前期進行數據評估及參數優化[3-5]。

1 P2構型組成

本文采用P2混動汽車作為建模的基礎，其所用混動總成的系統結構如下圖所示。

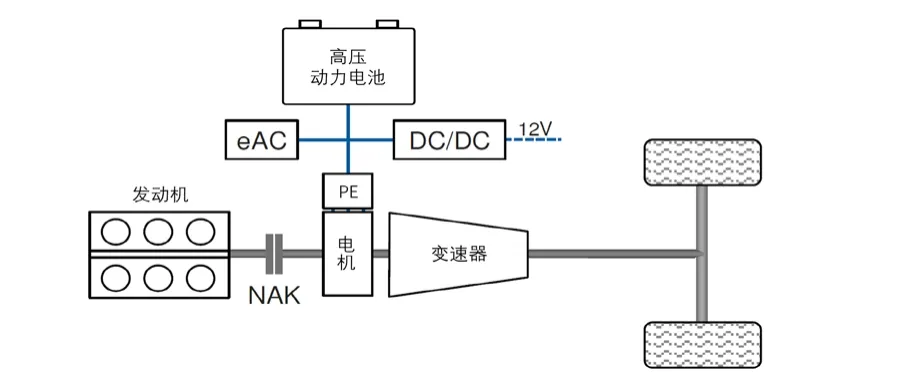
圖1 P2構型

該混動總成系統中的變速器的輸入軸未安裝變矩器，而是安裝了一個電機和一個啟動離合器（NAK）作為替代。位于電機和發動機之間的啟動離合器（NAK）既是啟動部件，又是動力分離部件，利用該部件可以實現發動機和其他部件的耦合及解耦。此處使用的電機為永磁同步電機，其通過功率電子器件（PE）連接至高壓動力電池。此外高壓電氣系統還包括車載空調系統（eAC）的制冷壓縮機以及DC/DC轉換器，該轉換器向12V低壓系統以及其他需要從動力電池獲取電能的用電器供電。

2 建立傳統系統數學模型

在對整車動力單元所需輸出的扭矩、轉速和功率進行計算時，根據計算過程中動力的流動方向可劃分為后向模型以及前向模型，此外還需對各機械部件以及電氣部件進行建模描述。

2.1 后向模型

如圖2所示為后向模型的原理示意圖，其特征在于，從輪端開始向驅動單元方向進行計算。根據行駛工況和駕駛狀態，可通過時域離散法來計算系統所需的扭矩、轉速以及功率，以此來滿足行駛工況。計算過程中不考慮車輛由于驅動功率限制而無法滿足行駛工況要求的情況。

圖2 后向模型的原理示意圖

車輛前進需克服的驅動阻力Fdrv,r包括滾動阻力Froll,r，空氣阻力Fair,r以及上坡阻力Fup,r，通過車輛參數（滾動阻力系數Froll，風阻系數Cw，前部投影截面A以及車身重量），并根據行駛工況所需的理論車速以及當前道路坡度即可得驅動阻力Fdrv,r的計算式如下：

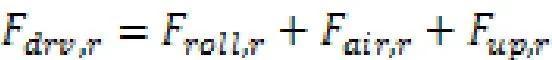
計算出變速器輸入端的扭矩后，接下來需解決發動機和電機之間的扭矩分配問題。扭矩分配由發動機的扭矩確定。根據離合器的狀態，電機的扭矩計算如下：

其中：

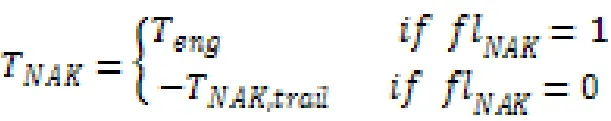
由于電機和變速器輸入軸直連，因此電機轉速就等于變速器的輸入轉速。

若離合器分離并啟動發動機，或者在離合器接合的情況下，發動機轉速低于空轉轉速nLL，那么可以認為發動機處于空轉狀態。

2.2 前向模型

與后向模型不同，前向模型則是根據驅動單元的驅動功率計算出輪端的輸出功率以及車速。其原理如圖3所示。但是由車速決定的轉速仍然是通過輪端反向計算得出的。該模型的扭矩和轉速都契合于實際整車，其能更好反映出傳動系統中的信息流和能量流。

為確定驅動單元所需施加的扭矩，以便使車輛能按照行駛工況行駛，前向模型還需增加一個駕駛員模型。在每一計算步驟中，按照PI控制器得出的駕駛員模型將實際車速vauto同行駛工況的理論車速vtheo進行對比，并據此輸出一個油門踏板位置夾角以及一個制動踏板位置。根據油門踏板位置夾角換算出扭矩需求，根據驅動策略就可以確定發動機、電機以及摩擦制動器所需施加的扭矩大小。考慮到各自的扭矩極

圖3 前向模型的原理示意圖

限，并根據離合器的狀態以及變速器和差速器的損耗和傳動比，就可計算出傳遞到輪端的扭矩TWheel：

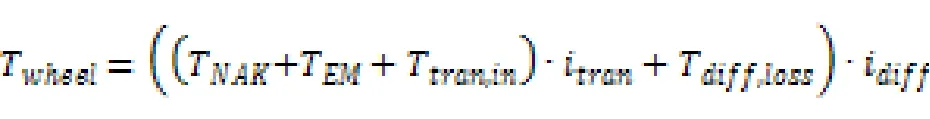
根據是正扭矩請求還是負制動請求，輪端扭矩Twheel要么是正，要么是負。可以計算出車速的變化率：

其中汽車等效質量meqv：

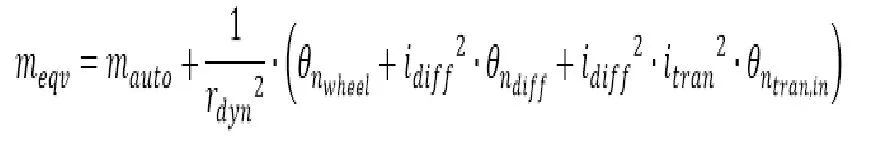
其中汽車等效質量由汽車平移加速質量mauto以及以輪端轉速、差速器轉速和變速器輸入轉速等旋轉部件的轉動慣性矩（計算過程中還需考慮到各自對應的傳動比）組成。

3 傳動系統部件建模

還需對傳動系統中的各部件進行建模。傳動系統部件的模型是準靜態的基于關系map圖的模型。除了在相應強調的位置有微小差異外，該傳動系統部件模型在前向和后向模型中都得到了應用。

3.1 差速器和變速器

后驅動軸差速器和變速器不僅可以用傳動比的形式來表示，也可以用輸入軸和輸出軸之間的損失扭矩來表示。差速器的扭矩損失Tdiff,loss可以根據輸入端的扭矩Tdiff、輸入端的轉速ndiff以及不同的油溫θdiff,oill計算：

而變速器的扭矩損失Ttran,loss還另外與擋位γ有關：

除了齒輪副、軸承、離合器等處的摩擦損失外，變速器的扭矩損失還包括用于油泵驅動所需的功率。所使用的數據來源于不同轉速和不同油溫下的損失測量。為了能額外考慮一個同負載相關的影響，該影響利用一個恒定的，和擋位有關的效率可以通過測量得到的關系圖來表示。換擋線是油門踏板位置夾角α和變速器輸出端轉速nDiff的函數。根據車輛是處于純電驅動模式（flNAK=0）還是混動模式（flNAK=1），并根據前向模型中的當前擋位γ來確定下一時刻的擋位選擇：

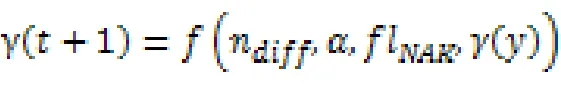
在后向模型中由于時域離散化計算，會立刻進行擋位切換，而在前向模型中則會延遲。另外傳動比關系是以正切雙曲線函數動態變化的。

3.2 離合器

在模擬仿真過程中，通常情況下都是采用純電啟動，因此離合器在純電驅動過程中充當著分離元件的角色，因此其被簡化為一個僅有兩種狀態的系統。在接合狀態下（flNAK=1）忽略滑磨影響，可以假設能量傳遞沒有損失。在分離狀態下則用拖曳力矩TNAK,trail表示，拖曳力矩和離合器片的差速以及變速器潤滑油溫θtran,oil有關：

拖曳力矩會隨著速差的增大而逐漸增大，也會隨著油溫的降低而逐漸增大，其原因為剪切應力隨著離合器摩擦片之間油液粘度和速差的增大而增大。

3.3 發動機

為了能盡可能在傳動系統中更換不同的發動機，以研究不同發動機性能帶來的差異，此處可以用靜態map圖來表示發動機的特性。在車輛設計階段最為重要的是對預研車輛的油耗進行評估，因此本文僅關注發動機在其工作溫度下的油耗，而忽略排放以及其他動態影響。研究油耗時是根據發動機的扭矩Teng和轉速neng 得出發動機的燃油質量流量的map圖。

此外，發動機的拖曳性能利用拖曳力矩Teng,trail描述，拖曳力矩取決于發動機轉速：

其描述了發動機在斷開狀態下（即切斷動力）的情況（fleng＝0）:

當對發動機的扭矩請求小于零且轉速大于轉速閾值nthre時，無論是扭矩還是轉速都在啟動閾值和關閉閾值之間存在一個遲滯，在這種情況下切斷動力的控制邏輯就會生效。在仿真計算中使用到的燃油質量流量的map圖以及拖曳力矩隨轉速的變化曲線可以利用臺架試驗得出。

3.4 電機

如同其他的傳動系統部件，電機連同其功率電子設備被構建成了一個靜態的map圖。這種關系是通過電功率PEM,el關于電機扭矩TEM和轉速nEM的函數來實現的。

與借助效率map圖的映射關系不同，此處描述的是零功率損耗或者說是在零扭矩損耗情況下的電功率需求。雖然后向模型的計算方法要求時域離散，但是通常沒有考慮其遲滯現象，在前向模型中也假定電機響應沒有遲滯，會立刻給出所設定的扭矩。

3.5 高壓動力電池

高壓動力電池使用等效電路模型以及map圖中存儲的電池參數來表示。圖4和圖5使用了兩種不同的建模方法：一種靜態模型以及一種動態模型。在計算時間和復雜度較高的情況下，動態建模具有以下優點：動態效應，如雙層電容，電荷交換或擴散的時間特性都能映射出來。在情況更為多變的實際行駛工況中，動態建模在仿真質量上更具優勢。因為后向模型法中需要進行時域離散計算，無法使用動態建模方法，因此此時要使用靜態建模。

圖4 動力電池靜態等效電路模型

圖5 動力電池動態等效電路模型

如圖4所示，動力電池靜態模型的等效電路圖僅由一個穩壓直流電源UOCV，以及一個串聯的電阻Ri組成。在混動汽車的仿真領域，這是一種常用的模型。利用基爾霍夫第二定理以及二次方程組求解，該模型的電池電流IBatt以及電池端功率Pter可用以下公式算出：

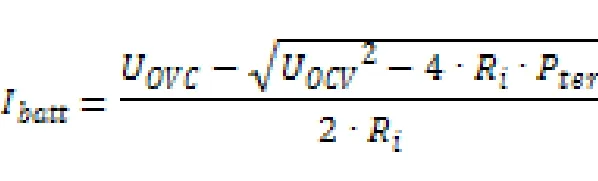
根據動力電池的容量Q0，可以在仿真過程中得到每一步的荷電狀態變化量△SOC：

△t是仿真步長。

此外，根據動力電池電流和開路電壓，可以計算出動力電池功率Pbatt：

與電池端功率Pter相比，Pbatt中還包含了充放電產生的電池損耗。

為了說明動力電池隨時間的變化特性，動態等效電路模型中增加了一個串聯的RC元件，見圖5。同根據電池功率給出的時域離散的電池電流相反，此處的電池特性可用下列微分方程描述：

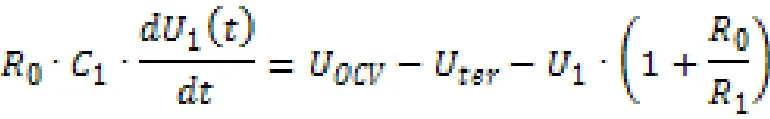
使用基爾霍夫定律也可從該等效電路圖中推導出該關系。

在兩個仿真模型中，靜態電壓UOCV和內阻Ri隨荷電狀態以及溫度的變化而變化。內阻大小根據電流方向（充電或放電）進行設定。穩態電壓隨荷電狀態的變化曲線以及動力電池內阻值大小的變化可以通過實際的測量得出一個相應的映射曲線。在靜態等效模型中，內阻值的大小通過10秒內充電或放電1C時的電壓降來確定。而在動態等效模型中，電阻R0則是使用0.1s內的值，因此此處的動態特性是通過RC元件來建立的。與10s的值相反，這些（0.1s）值幾乎僅包括歐姆電阻。雖然這些值來自電池的測量值，但RC元件的值是通過將仿真出的電池電壓與在不同驅行駛工況下測得的電壓進行比較確定的。

4 結論

本文以P2混動汽車作為研究對象提出一種傳動系統的數學建模方法，利用該傳動系統的數學模型可通過研發階段的建模仿真來分析研究P2混動汽車的驅動模式切換策略以及整車所需輸出的扭矩及扭矩分配、轉速和功率等，此外還可借助該數學模型計算整車的燃油經濟性，作為汽車研發過程中的方向基礎。