UKF估計器對IPMSM 無傳感器控制的比較研究

SHEIANOV Aleksandr, 康爾良

(哈爾濱理工大學，哈爾濱150080)

0 引 言

永磁同步電動機(以下簡稱PMSM)無傳感器測量技術由于消除了位置傳感器易碎、噪聲大、成本高等缺點，受到了國內外學者的廣泛關注[1-2]。該技術通過測量定子側的電壓和電流信息，并結合相關算法，估算出轉子的位置信息。轉子位置和轉速的準確估算是影響這類系統性能的關鍵。

卡爾曼濾波器系列中有許多類型的觀測器。卡爾曼濾波器最初是線性類型的估計器，也稱為線性二次估計器(以下簡稱LQE)。卡爾曼濾波器是以Kalman R命名的，也就是這個理論的開發者[3]。卡爾曼濾波器在所有線性估計器和觀測器中具有最好的性能，在飛行器，特別是飛行器和航天器的制導、導航和控制等領域有著廣泛的應用。至于非線性問題，卡爾曼濾波器家族也提供了許多不同的方法[4]。迄今為止，研究最多的是擴展卡爾曼濾波器，它首先根據先前的估計來計算預測狀態，然后以相同的方式，輸出函數h根據預測狀態來計算預測測量值。然而，這種濾波器的f和h不能直接應用于協方差，因此，需在每個時間步長中[5]計算偏導矩陣(雅可比矩陣)。雖然EKF(Extended Kalman Fitler)應用于電機控制是相對簡單的，但它有許多主要缺點:線性化過程中雅可比矩陣的推導比較復雜；因為忽略了高階項，EKF僅具有一階精度；線性化引起的濾波器不穩定性。

為了消除這些問題，使非線性卡爾曼濾波器族比其他非線性算法更精確、更優越，Julier和Uhlmann[6],提出了一種改進非線性卡爾曼濾波器性能的新方法。無跡卡爾曼濾波器(以下簡稱UKF不是在每個時間步長對非線性系統進行線性化(求解雅可比矩陣)，而是使用樣本點的最小集合，這些樣本點被饋送到非線性狀態方程，以獲得預測步長中非線性系統的均值和協方差，然后根據新的測量結果來校正預測估計值。UKF已成功地應用于導航、雷達跟蹤、信號處理、神經網絡和機器人等實際應用[7-8]。AKIN[9]報道了UKF在電機控制中的首次實現。Borsjie P等人[10]報道了UKF在PMSMd-q參考系下的無傳感器矢量控制應用；Titaouine A,Taibi D[11]結合逆變器的非線性控制；Cheol Moon, Kee Hyun Nam[12]在α-β參考系中實現了該算法。然而，到目前為止，關于UKF在內置式永磁同步電機(以下簡稱IPMSM)應用中的論文寥寥無幾。

目前，對滑模觀測器已經進行了大量的研究，這些研究都表明在實時應用中實現這種方案的潛力很大[13]。滑模觀測器在商業產品中已被廣泛使用，因為其簡單，顯示出相對良好的性能，并且可以在廉價的定點DSP上實現，從而降低了產品的成本和尺寸。然而，在低速范圍內它表現出較差的性能，這在一些應用中是非常關鍵的因素，因此有學者提出通過起動技術[14-15]以及高頻注入方法[16-20]來增強滑模觀測器，規避起動的問題。這在低速范圍內這增加了無傳感器方案的計算量和復雜性。

本文是對上述文獻的擴展。此外，本文還對UKF和滑模觀測器進行了比較，在MATLAB/Simulink中進行了仿真，表明這兩種算法在性能上有明顯的差異。

1 PMSM數學模型

卡爾曼濾波器需要該系統的數學模型，以便估計系統的狀態。受控系統數學模型的制定是估計器設計階段的一項重要任務。正確的模型不僅可以簡化估計問題的求解，而且可以簡化整個算法的計算量。

為了避免起動時的收斂問題和簡化電機方程，選擇d-q參考系來評估卡爾曼濾波器[2]。電機非線性狀態方程可以表示：

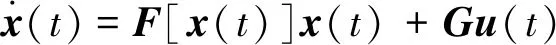
(1)

y(t)=Hx(t) (2)

式中：輸入向量u=[uduq]T；輸出向量y=[idid]T。UKF由4個狀態變量組成：靜止參考幀電流、估計速度和估計角度。由于機械變量有快速變化的趨勢，并且很難正確測量，所以狀態變量僅由電變量組成。狀態變量向量x=[idiqωeθe]T。通過取式(1)和式(2)中的偏導，我們可以寫出系統狀態矩陣：

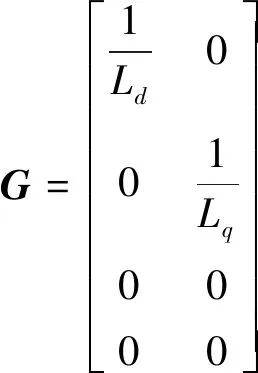
2 UKF

對于使用UKF的PMSM無傳感器控制，電機非線性狀態方程式(1)和式(2)應以離散形式：

xk+1=Fd(xk)xk+Gduk+Bwwk(3)

yk=Hdxk+vk(4)

式(3)和式(4)所表示的狀態模型還包括對誤差的統計描述，其中wk～N(0,Qk)和vk～N(0,Rk) 分別是協方差矩陣Qk和Rk的零均值高斯過程噪聲和測量噪聲向量。

2.1 無跡變換

無跡變換的設計是基于這樣的事實，即近似概率分布比近似非線性函數(后面是EKF所基于的原理)更容易。關鍵是在高斯輸入的情況下，近似精確到第三階。對于非高斯輸入，近似精確到至少一個二階。因此，UKF期望比僅具有一階精度的EKF提供更好的性能和精度。

西格瑪點集：

(5)

式中：L是維數。

加權：

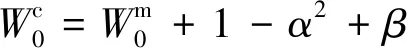
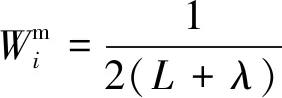
式中：λ=α2(L+κ)-L，λ表示縮放參數；上標m，c表示均值和協方差計算的加權點；α決定了西格瑪點在x附近的擴展，10-4<α≤1；常數κ是另一個標度參數，通常設置為κ=3-L；β是x分布的先驗知識(對于高斯分布β= 2是最優的)。

每個點通過非線性狀態轉移和測量函數傳播，以產生一組變換后的點：

Yi=g(χi)i= 1,…,2L(6)

用加權平均值和協方差近似y的均值和協方差：

(7)

2.2 UKF算法

UKF是無跡變換遞歸卡爾曼濾波方程的直接應用。UKF流程如圖1所示。

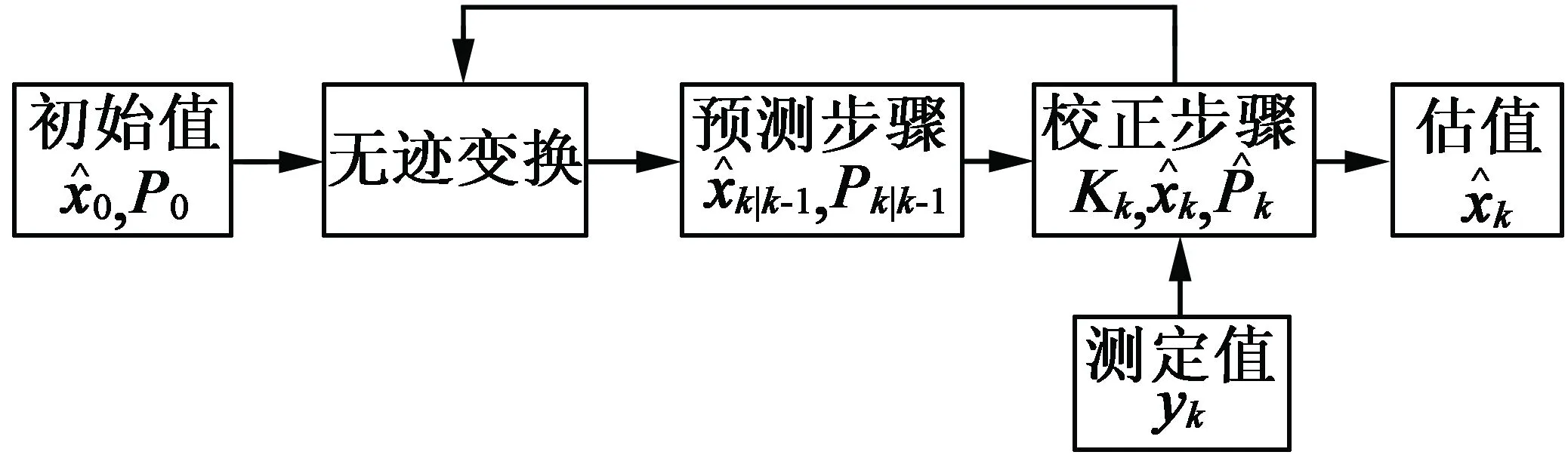
圖1 UKF框圖

UKF算法包括以下步驟：

(1) 計算西格瑪點的集合。

(2) 通過非線性PMSM模型傳播西格瑪點：

χk|k-1=f(χk|k-1;uk|k-1)

(3) 計算預測平均值：

(4) 計算預測協方差：

(5) 通過觀測模型對每個預測點進行變換：

Yk|k-1=h[χk|k-1]

(6) 計算預測觀測的加權平均值：

(7) 計算創新協方差矩陣：

(8) 計算互協方差矩陣：

(9) 校正步驟使用正規卡爾曼濾波方程進行更新。

卡爾曼增益：

Kk=Pxk ykPykyk-1

修正估計狀態：

校正協方差

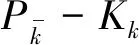
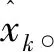
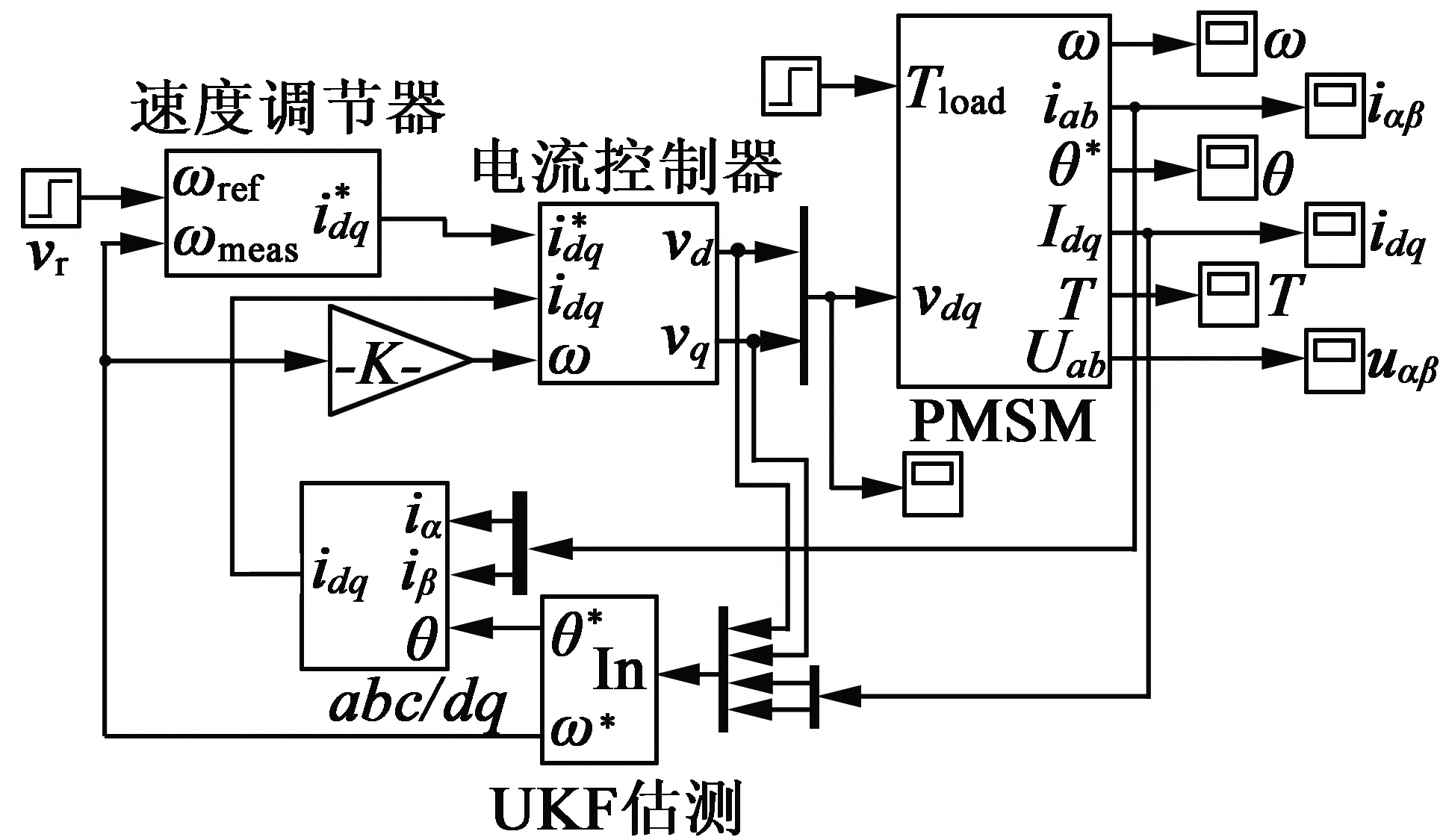
圖2 基于UKF估計的無傳感器閉環系統

3 滑模觀測器

本文對無傳感器滑模觀測器作簡要的說明，然后在MATLAB/Simulink中進行仿真。這種控制算法的完全推導、改進和結果可以參照文獻[16]。

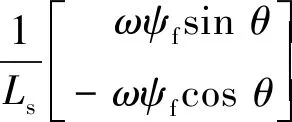
式中：iα和iβ表示的是在靜止參考系中被測定子電流；uα和uβ表示的是在靜止參考系中PMSM所施加的電壓。定義x= [x1,x2]T= [iα,iβ]T，eα=ωψfsinθ，eβ=-ωψfcosθ，在α-β中的PMSM的狀態空間模型：

(9)

采用滑模觀測器的目的是在不知道電機實際轉子位置和速度的情況下調節電機速度，即實現PMSM的無傳感器控制。同時，為了避免抖動，將傳統的滑模觀測器中的符號切換函數由以下飽和函數代替：

(10)

通過在滑模觀測器中應用飽和函數，定義的滑動變量可以在有限時間內到達邊界層，并在邊界層中停留。估計模型如下：

(11)

從式(9)和式(11)，可以導出以下關系：

(12)

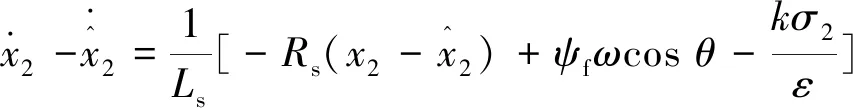
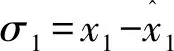
(14)

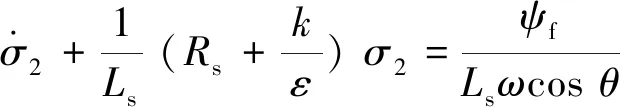
將上述方程經過拉普拉斯變換之后，可以得到以下傳遞函數：

(16)

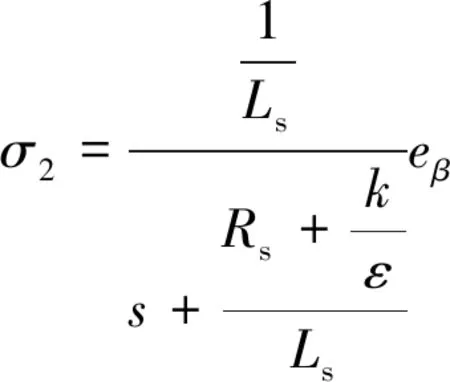
由變量σ1和σ2定義的滑動面可視為eα和eβ的濾波信號。因此，利用這一原理，我們可以提取轉子的位置信息，然后使用鎖相環方案，計算出轉子速度。下面將比較兩種無傳感器控制方法。

4 仿真結果

通過兩種算法的仿真來驗證所提出算法的性能，從中可以得到一些明顯的差異。仿真中使用的IPMSM的參數如表1所示。

表1 IPMSM參數

圖3是用滑模觀測器模擬的。從系統的速度響應可以看出，在低速區域，特別是700 r/min時，系統存在一些振蕩。這是這種類型的觀察器的一種常見行為，表明它不能應用于一些低速應用。而700 r/min后，可以高精度跟蹤速度和角度，并且具有較小的誤差，在額定速度下可以忽略。整個系統顯示出較好的性能，但在實際應用中還需要一些起動算法，如：I-f起動或高頻注入。運行到600 r/min后，切換到滑模觀測器跟蹤算法。

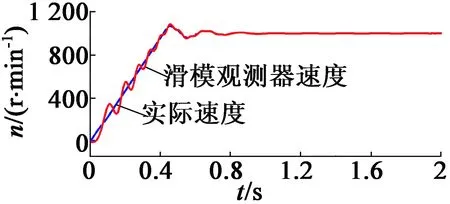
(a) 實際和滑模觀測器速度響應

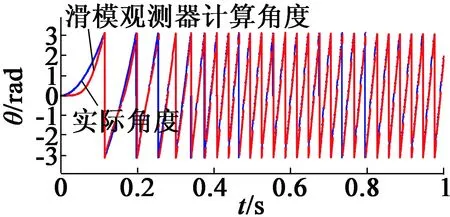
(b) 實際和滑模觀測器計算的角度

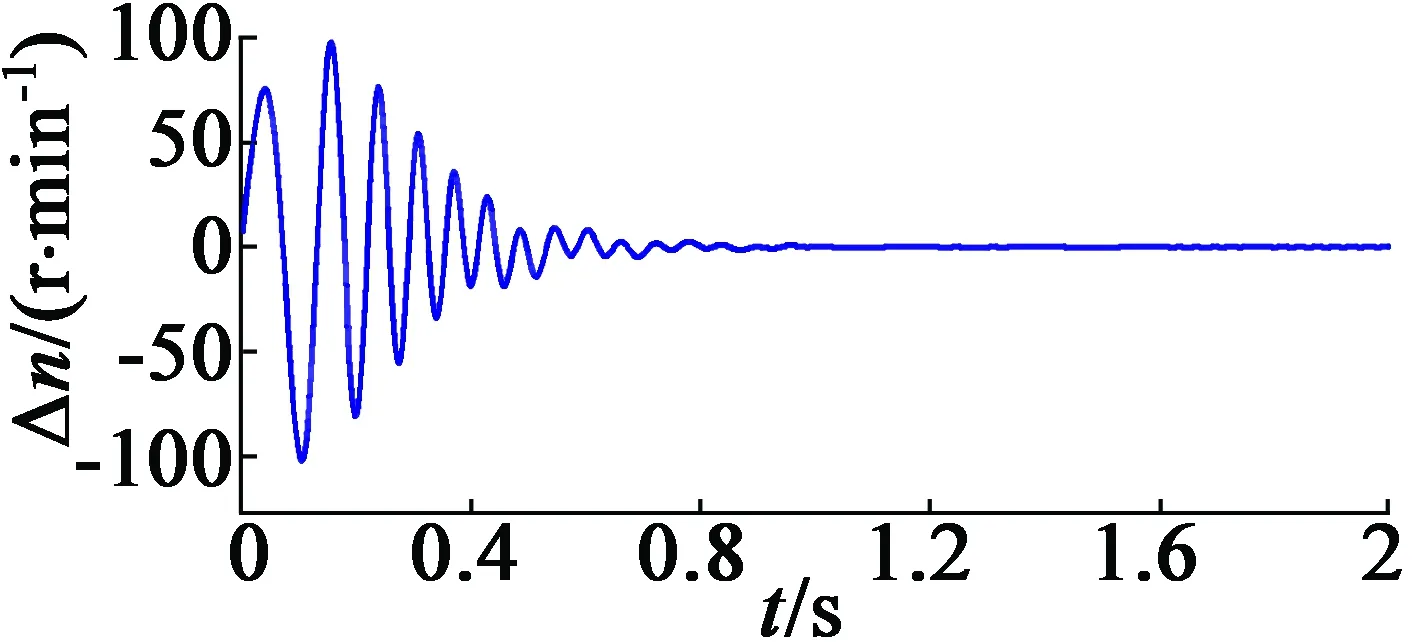
(c) 實際速度與滑模觀測器之間的誤差

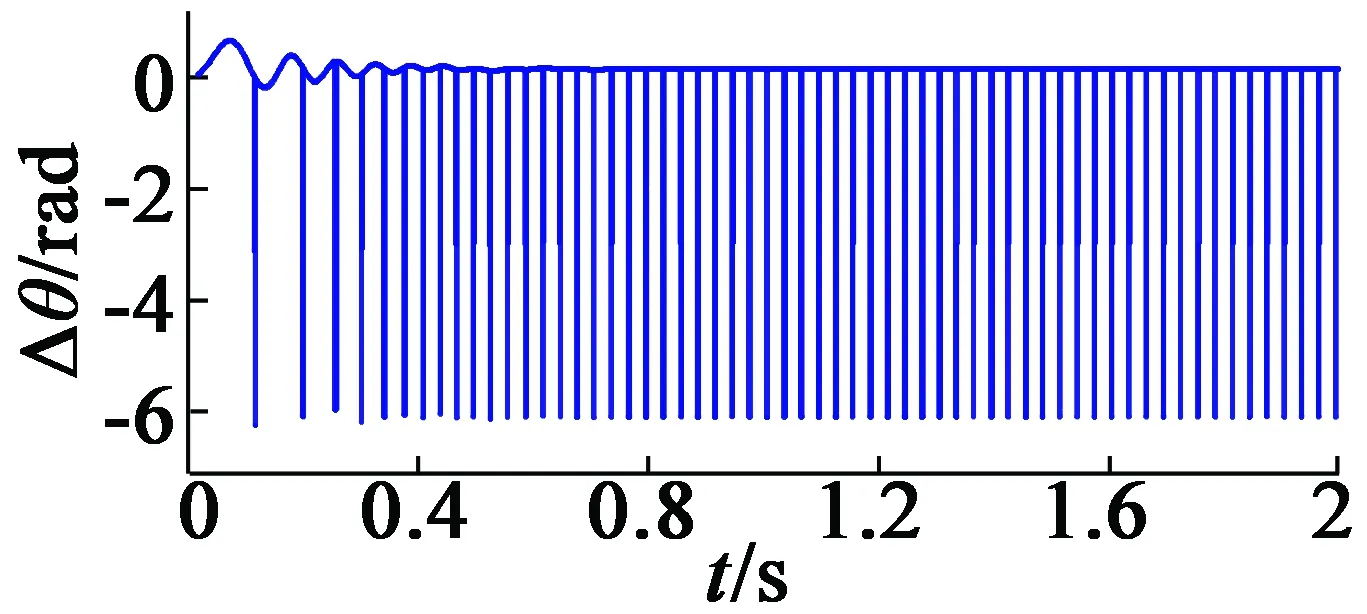
(d) 實際 θ角度和滑模觀測器計算之間的誤差

下面闡述UKF算法以及其特點。為了驗證所提出的算法，在系統運行0.5 s之后增加一半的額定負載。從圖4(a)可以看出，UKF在低速區域以及中高速區域顯示出了更好的性能，并且完全跟蹤真實的系統速度響應。如圖4(b)所示，UKF的速度誤差更小，這也進一步證明了上述結論。

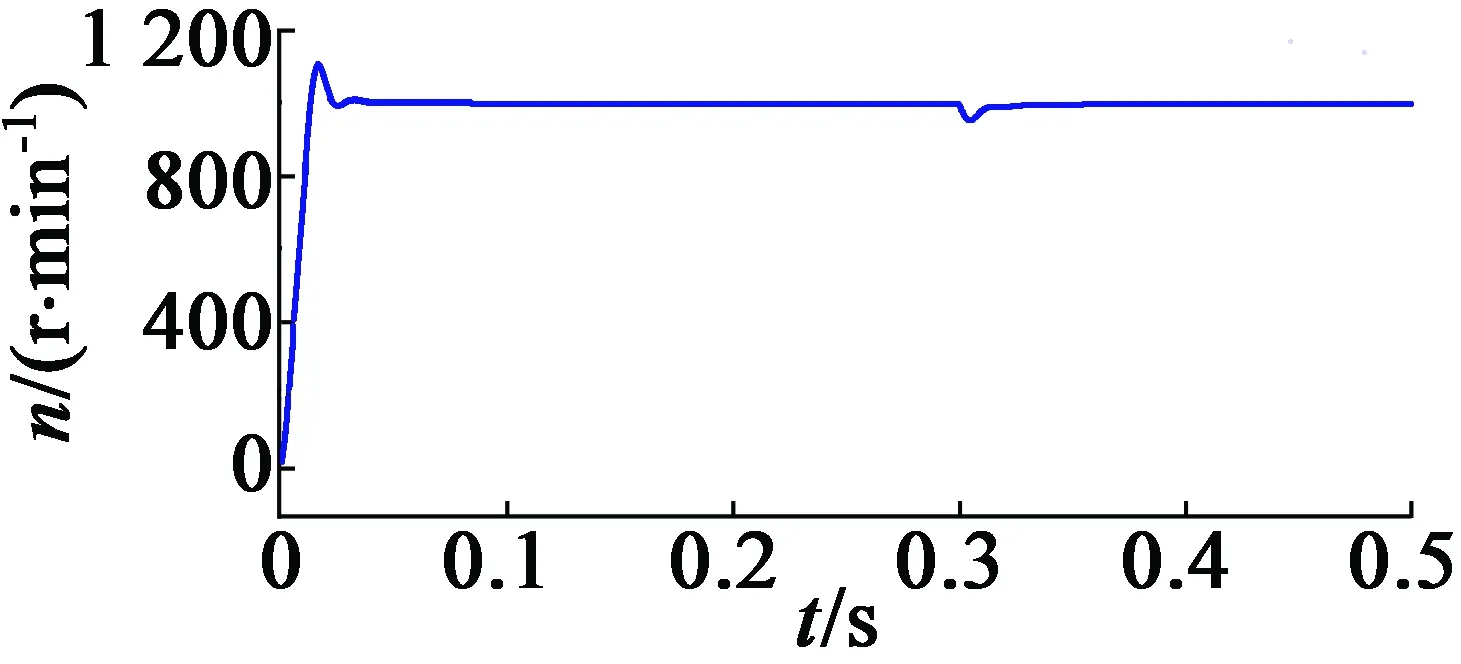
(a) 實際和UKF系統速度響應

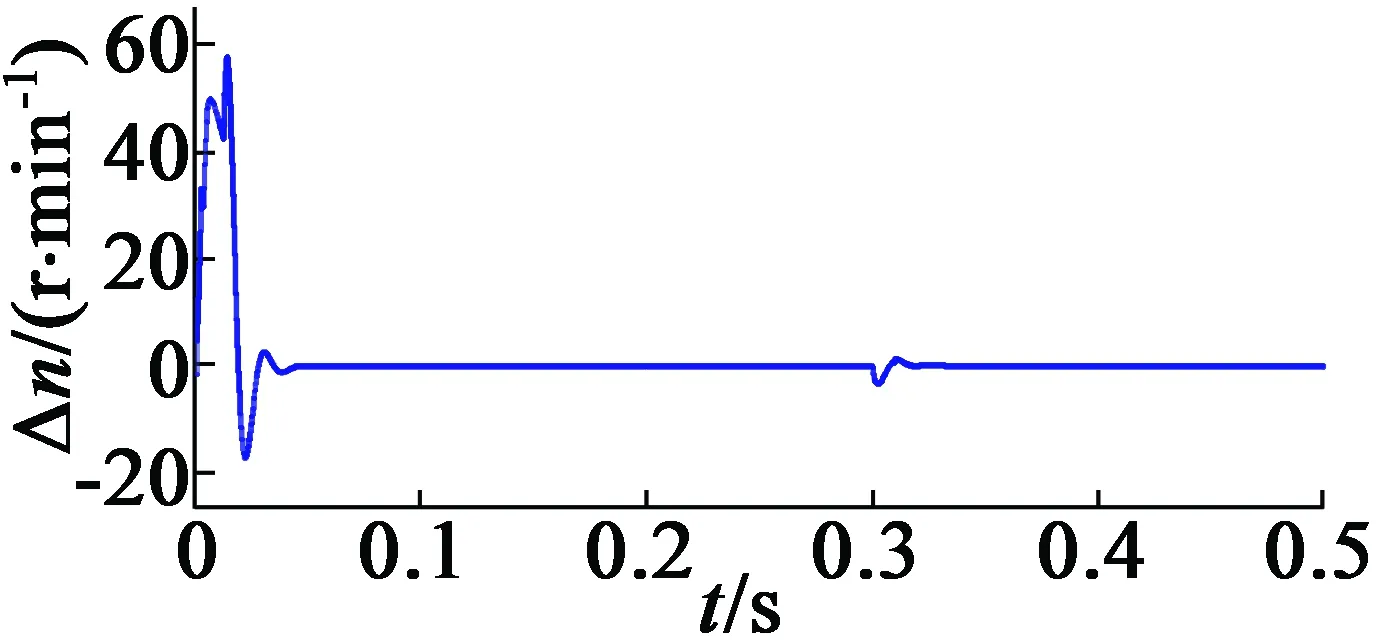
(b) 實際和UKF系統速度誤差

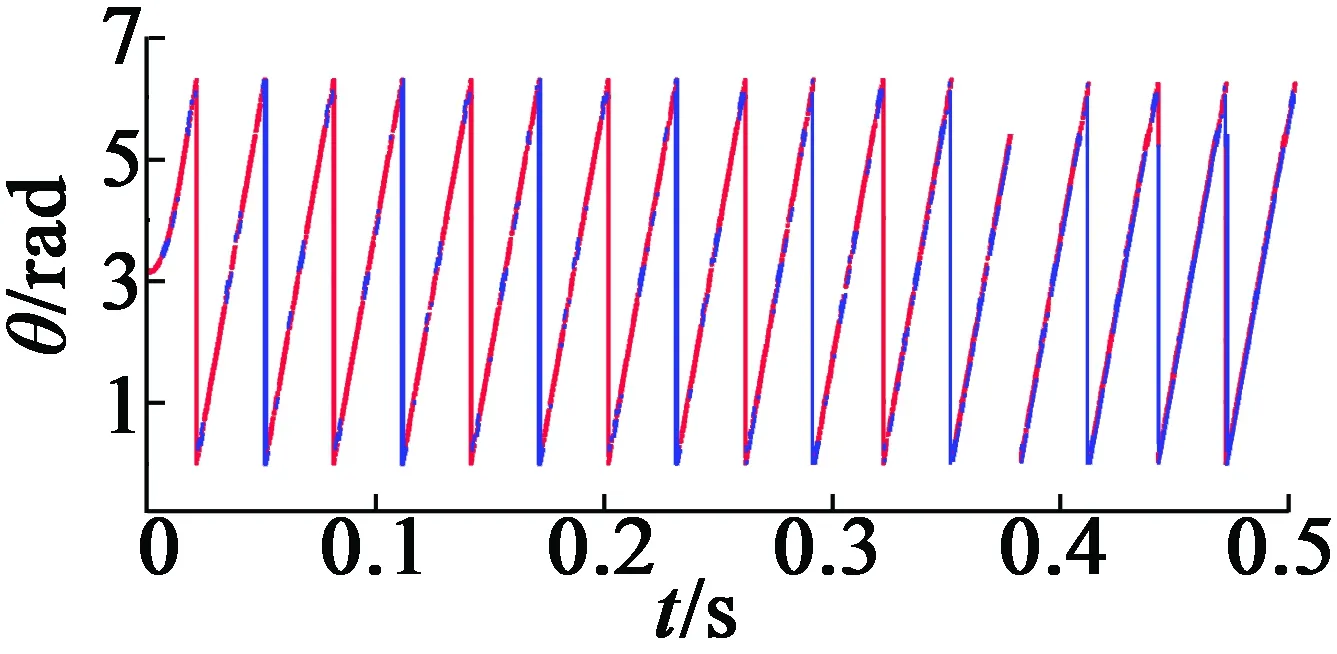
(c) 實際和UKF系統角度響應

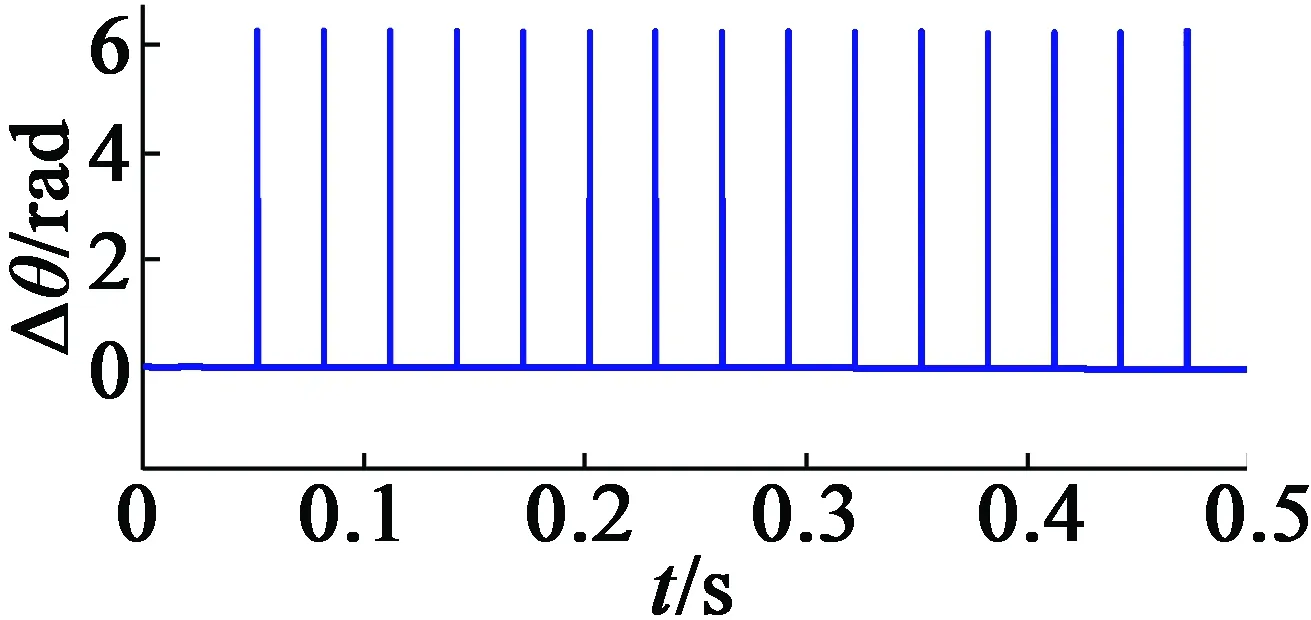
(d) 實際系統和用UKF計算之間的角度誤差

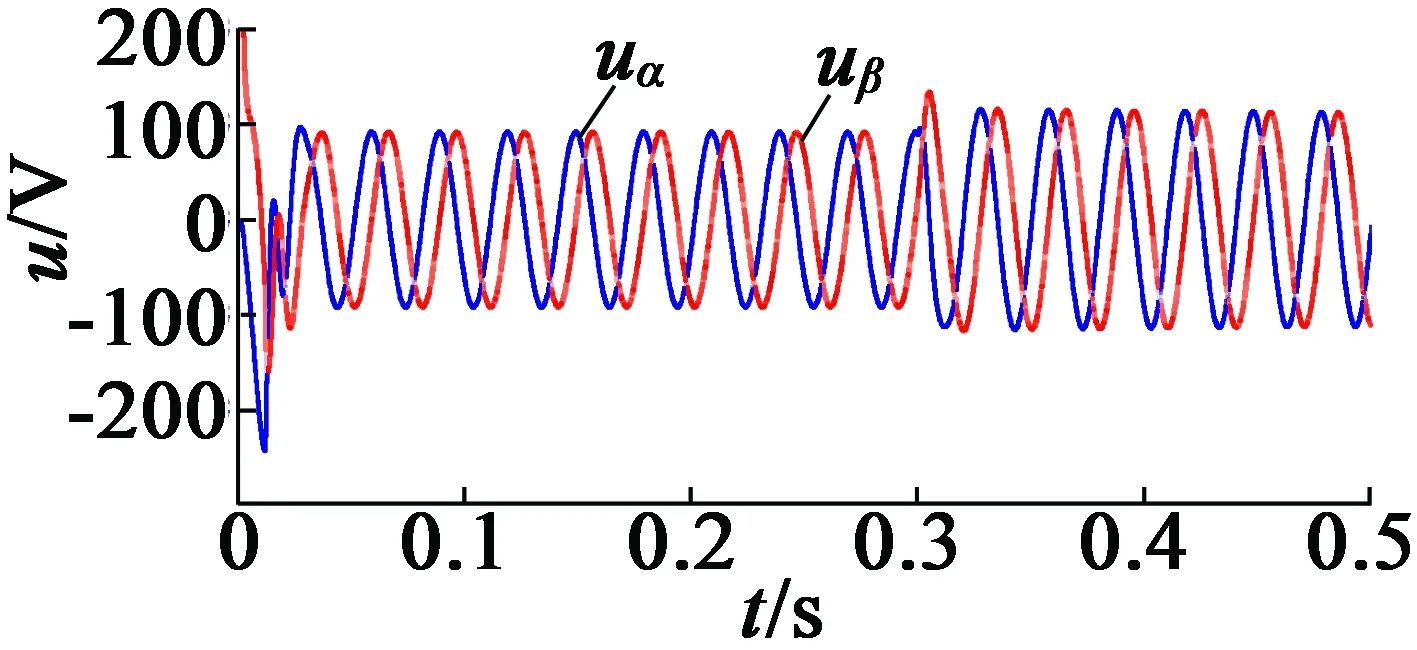
(e) UKF系統的電壓響應

理論上，由于UKF的噪聲抑制能力，在電機低速情況下，與基于滑模觀測器的轉子位置估算結果相比，UKF能夠提供更可靠的轉子位置估計。圖5(a)和圖5(b)中，基于UKF估算轉子位置時，在電機低速運行的情況下，d-q軸電流估算結果噪聲較少，這與UKF的噪聲抑制能力有關。從圖5(c)可以看出，在電機轉速高于100 r/min后，可得到準確的轉子位置估算結果。因此，在本文控制算法中，首先通過預設頻率、幅值可調的電流矢量將電機轉至100 r/min(有些文獻中稱為I-F控制)，此后切換至基于UKF的無傳感器閉環控制算法。基于上述控制方法，可使電機由靜止快速切換至閉環控制，較大地縮短了起動時間，適用于對起動時間要求較快的場合。

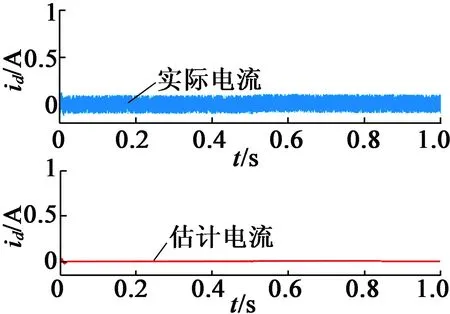
(a) 實際和UKF估計的Id電流響應

(b) 實際和UKF估計的Iq電流響應

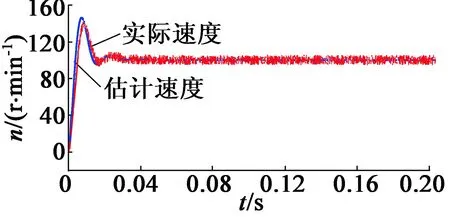
(c) 實際和UKF系統低速響應

但是，系統的唯一缺點是它不能在定點處理器上實現，因為算法不能保證狀態協方差矩陣的收斂。但在TI TMS320F28335的浮點處理器上，可以較容易地實現，該芯片的時鐘頻率為150 MHz，具有足夠的資源在一個中斷期間內計算整個無傳感器控制算法。

5 結 語

本文對基于UKF的無位置傳感器PMSM驅動系統進行了研究。與滑模觀測器的比較表明，UKF在低速區域給出更精確的位置和速度估計，而且由于不需要使用附加的起動技術，UKF可以應用于更廣泛的領域。特別地，UKF在跟蹤瞬變期間的速度方面執行得更好。同時，對于PMSM驅動器內存在的噪聲，UKF的性能優于滑模觀測器，并且在擴展速度范圍內控制仍然有效。UKF算法比滑模觀測器更復雜，因此運算量要大得多。為了成功實現基于UKF的無傳感器PMSM驅動，必須選擇高性能的DSP。