大型軸流泵站超駝峰運行過渡過程研究

汪尚紅，李 澤，高超丹，莊克云

(1.湖北省金口電排站管理處，武漢 430209；2.武漢大學動力與機械學院，武漢430072)

軸流泵揚程低、流量大，出水流道分虹吸式、直管式及屈膝式。其中虹吸式出水流道由于其結構特點，被廣泛使用，在外江水位低于駝峰底部高程的情況下，可起到斷流擋水的作用。然而，受自然條件、河床淤積等原因的影響，外江水位逐年上升，此時，出水流道駝峰已失去切斷水流的功能。一方面，當發生內澇災害時要求泵站開機運行，另一方面，防洪期間又要求泵站停止向外江供水，因此，泵站在超駝峰水位下運行就不可避免。由于泵站超駝峰運行經常在超高揚程下運行，負荷較重，振動較大，并且一旦發生事故停機，將出現斷流難度大，出現斷流失效現象，最終將進入飛逸狀態。因此，為確保軸流泵機組在超駝峰水位下正常運行，進行水泵機組在超駝峰運行的過渡過程研究是很有必要的。

對泵的過渡過程研究，現已有不少研究成果。周大慶[1]考察了出水管道采用平直管式，斷流裝置為快速閘門帶小拍門形式的軸流泵啟動特性，并計算了機組牽入同步的時間。于永海[2]基于水量平衡和水泵力矩方程，采用水泵全特性曲線，建立了立式軸流泵機組在啟動過程中的數學模型。陸偉剛[3]從機組停泵動態過渡過程著手，通過忽略正轉正流階段水流慣性對閘門運行的影響，建立了快速閘門下落運動的數學模型，得到了停泵后瞬時倒泄流量與快速閘門下落高度及下落時間的關系。

考慮到軸流泵管道一般較粗且較短，故可忽略管道彈性、水體可壓縮性影響，在水錘分析中，一般采用剛性水錘理論。本文以泵機組動力學特性、泵裝置水力特性及機械特性等建立泵在啟停過程中的數學模型，研究出水流道為虹吸式的軸流泵機組在超駝峰水位下的水力瞬變過程，確定外江極限運行水位及停機時出水閘門的最優關閉過程，以便為大型立式軸流泵站啟停機控制提供建議。

1 數學模型

1.1 啟泵過渡過程

軸流泵機組啟動過程可分為兩個階段：第一階段為出水閘門打開，機組從轉速為0上升至額定轉速牽入同步階段；第二階段為出水管道充水、造壓及揚水過程，直至出水閘門全部打開為止。水泵機組在啟動過程中，其轉子所受力矩主要包括動力矩和阻力矩。動力矩即電動機的電磁力矩，阻力矩主要有軸承摩擦力矩、水阻力矩及各種損失力矩。這些力矩的大小取決于泵系統的電氣特性、機械特性、水力特性及空氣動力特性。式(1)中的F1、F2和F3為根據這些特性，得到的出水流道為駝峰形的軸流泵機組在啟動過程中的數學模型。

(1)

式中：Mm為電動機最大異步轉矩；Sm為對應于Mm下的臨界轉差率；U0為電動機定子端瞬時電壓；Um為啟動瞬時定子端電壓；K、h為常數，其值為0.6～0.8及5.0～6.5；t為啟動時的時間；T為從啟動到牽入同步的時間；Q、H、n、n0、η、M分別為流量、揚程、轉速、同步轉速、效率及力矩；f為軸承摩擦系數；G為作用于推力軸承上的所有軸向力；R為推力軸承鏡板的平均半徑；ML、Mc分別為流道上升段特性參數及下降段特性參數；ΩJ為泵葉輪中水流的旋轉慣性系數；ΩM為泵葉輪中水流的流動慣性系數；λ為駝峰以前充水管段水力摩擦系數；A、B、C均為常數；S為上升段流道內水平面面積；P為流道內氣壓；P0為流道內初始氣壓；V0為流道內初始空氣體積；Hc為出水面與下降段管段內水面差。

寫成一般的函數表達式，式(1)可表示為：

(2)

式(2)中只有轉速n、流量Q、流道內氣壓P和時間t為獨立變量，其余均為非獨立變量，因此，式(2)存在唯一解，可利用積分試算法和分段試算法[4]進行求解，兩種計算方法在時間段Δt很小的情況下，有較好的精確度，但計算工作量大，為此本文利用MATLAB編制源程序對其進行求解。

1.2 停泵過渡過程

1.2.1 水泵全特性描述

目前水泵全性能曲線通常采用P.Suter、Marchal等學者提出的方法，橫坐標以無因次坐標參數x表示[5]，縱坐標為WH(x)、WM(x)。

(3)

(4)

式中：Q、n、H、M分別為泵流量、轉速、揚程及轉矩，下標e表額定值。

為方便計算機調用WH和WM的值，通常從x=0至x=2π，以等分間距Δx=2π/88=0.071 4，從兩條全特性曲線上取下89對離散數據。當計算過程中出現的x值位于兩個離散數據之間時，可通過線性內插，由插值點左邊的數據點號I和右邊I+1點確定出WH(x)和WM(x)的值。其中，I=INT(x/Δx+1)(INT表示x/Δx+1的整數內容)。

兩節點間的微段曲線可用通過兩節點的直線近似替代，微段曲線近似表示為：

(5)

(6)

式中：A0、A1、B0、B1均為常數。

1.2.2 水泵端邊界條件

由剛性水錘[6]及水泵全特性理論，停泵工況下，泵端邊界條件方程可由水頭平衡方程和機組轉速改變方程兩個方程表示。現用F1表示水頭平衡方程，F2表示機組轉速改變方程：

(7)

式中：β、v分別為ti+1時刻的相對轉速和相對流量；β0、v0、m0分別為ti時刻的相對轉速、相對流量和相對轉矩；Hsy為泵裝置揚程；S為阻力系數；ML為流道慣性系數；C1、C2均為常數。

(8)

式中：J為轉動慣量。

以上兩個方程中都含有未知數v、β，通過聯立求解，可解出流量和轉速，但在此處的兩式只能通過迭代的方法來求其近似值，因為其為非線性的超越方程。此處采用Newton-Raphson迭代公式來進行方程的數值求解。其迭代公式如下：

(9)

1.2.3 閘門端邊界條件

當閘門采用兩階段關閉規律時，設閘門的快關時間為T1、快關行程為H1、慢關時間為T2，慢關行程為H2，則在任意時刻t閘門關閉高度L為：

(10)

通過閘門的孔口流量Q可按下式計算：

(11)

式中：μ為流量系數，一般是閘門(閥門)開度的非線性函數，正流時取“+”，逆流取“-”；b為閘門寬度；e為閘門孔口開啟高度；ΔH為水頭損失。

2 工程案例

2.1 泵站基本情況

研究所用泵站為湖北省金口泵站，泵站原裝6×1 600 kW，現為6×2 200 kW，水泵為2800ZLQ24-7型全調節軸流泵，其主要技術參數為：設計流量Qn=24 m3/s，設計揚程Hn=7.0 m，額定轉速Nn=150 r/min，額定點效率為87%，水泵轉動慣量為2 846 kg·m2，水泵揚程適應范圍為0.1～8.5 m，葉片角調節范圍為-12°～6°，配套電機為TL2200-40/3250型同步電動機，配套功率2 200 kW，對應電機轉動慣量為18 500 kg·m2。設計提排流量原為120 m3/s，現為144 m3/s，是一座Ⅱ等大型泵站。泵站自建成投入運行以來，為金水流域的排澇發揮了巨大的效益。

2.2 水泵全性能曲線改造

水泵全性能曲線通常由專門的實驗測得，現有實測資料的軸流泵全性能曲線非常少，為得到任意比轉數下的軸流泵全性能曲線，本文以比轉數Ns=260、333、530、950四種水泵的全面性能曲線資料進行分類三次多項式擬合[7]，擬合系數見表1和表2。圖1為采用此分類三次多項式擬合得到的比轉數Ns=623水泵全性能曲線。

表1 擬合系數aTab.1 Curve fitting coefficients

表2 擬合系數bTab.2 Curve fitting coefficients

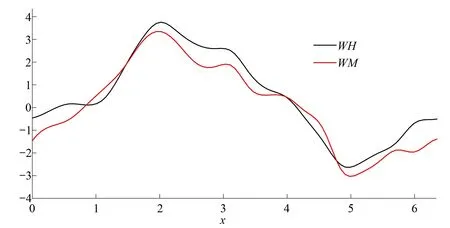
圖1 比轉速Ns=623的水泵全性能曲線Fig.1 The full characteristic curve of pump with specific speed Ns=623

3 水泵啟動過渡過程計算

軸流泵裝置由于其在關死點處軸功率處于最大狀態，因此在啟動過程中，需要開閘啟動，而閘門的啟動速度對軸流泵啟動過渡過程的影響需具體分析。

為保障軸流泵的正常啟動，現以最不利工況，即在最大凈揚程(H=7.05)下計算不同閘門開啟速度對系統造成的影響。根據計算結果繪制機組啟動最大功率及最大倒泄流量與閘門開啟時間之間的關系曲線如圖2所示。

圖2 最大倒流流量和最大啟動功率與開閘時間之間的關系曲線Fig.2 The max reverse flow rate and max power in different sluice gate opening time

從圖2可以看出。隨著閘門開啟時間的延長，最大倒流流量在逐漸減小，其中閘門在20～90 s開啟時，最大倒流流量減小明顯，超過90 s后，最大倒泄流量變化減弱；最大啟動功率隨閘門開啟時間增大而增大，當閘門60 s開啟時，最大啟動功率為2 199.2 kW，尚小于配套電機額定功率，因此為保證泵的正常啟動，閘門開啟時間不應超過60 s。

現以閘門開啟時間為50 s時對泵啟動過渡過程進行計算，其系統參數隨時間的變化曲線如圖3所示。從圖3可以看出泵在啟動過程中，泵轉速逐漸上升，大概在8 s左右到達額定轉速150 r/min；泵流量剛開始處于倒泄狀態，其最大倒泄流量為5.9 m3/s，之后隨著泵轉速的增大，泵流量在5.6 s左右開始正流，之后流量穩定在22.6 m3/s；電機最大啟動功率為2 186.6 kW，小于電機的額定功率，滿足啟動要求。

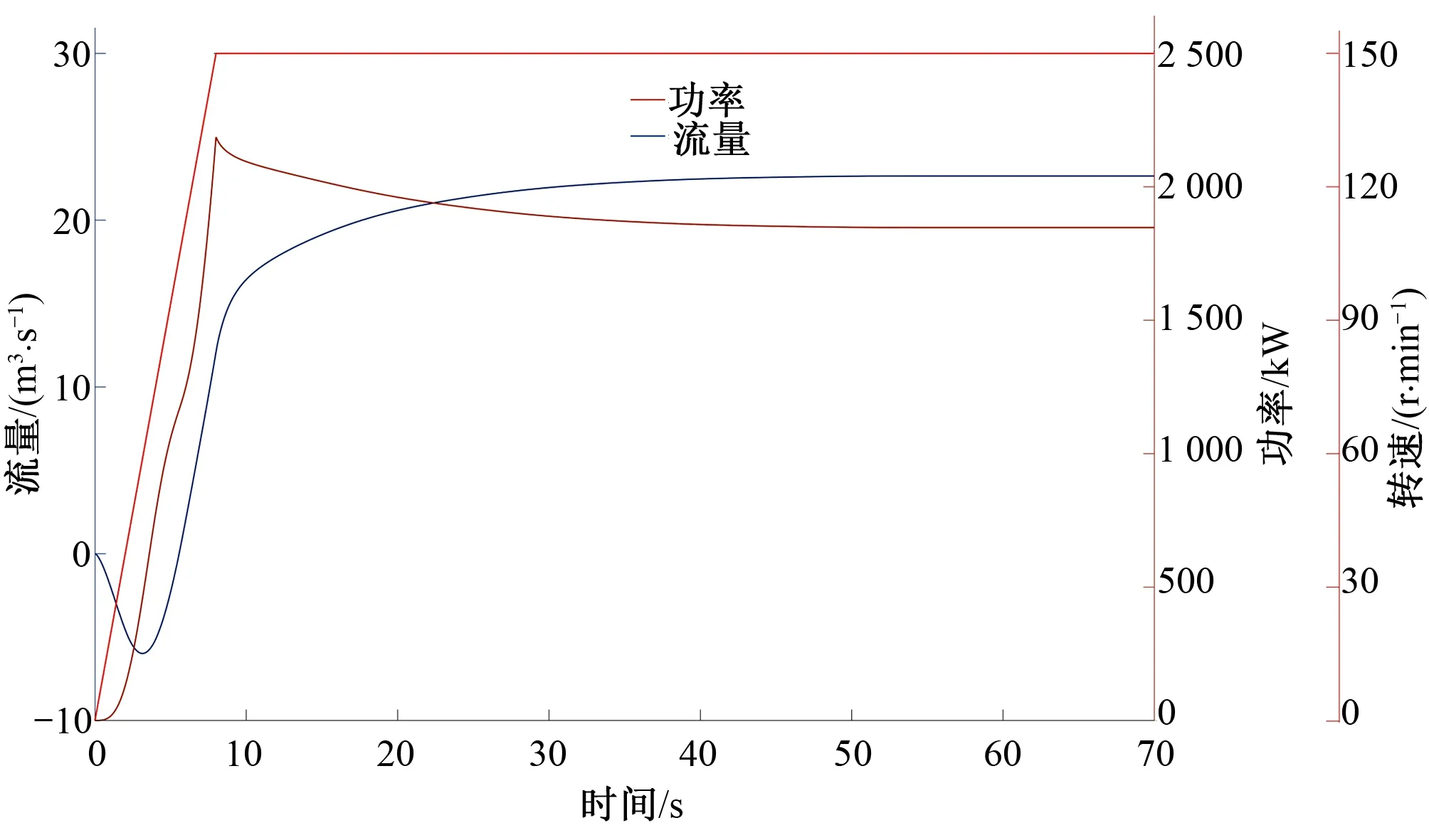
圖3 閘門50 s開啟時流量、轉速和功率隨時間變化曲線Fig.3 Flow rate, rotational speed and power versus time curve when the sluice gate opened for 50 s

4 水泵停機過渡過程計算

4.1 機組事故停機

金口泵站興建的年代較早，設計標準較低，最大運行揚程較小，外江最高運行水位較低。因此，外江水位超過虹吸出水流道駝峰高程的現象頻繁發生，此時，出水流道駝峰已失去斷流擋水功能。為確定外江極限運行水位，現對金口泵站在出口閘門不關閉、駝峰頂部真空破壞閥不打開，內河水位為24.59 m的情況下，計算外江水位超駝峰0.5、1.0及1.5 m下轉速和流量隨時間的變化過程，計算結果如圖4所示。

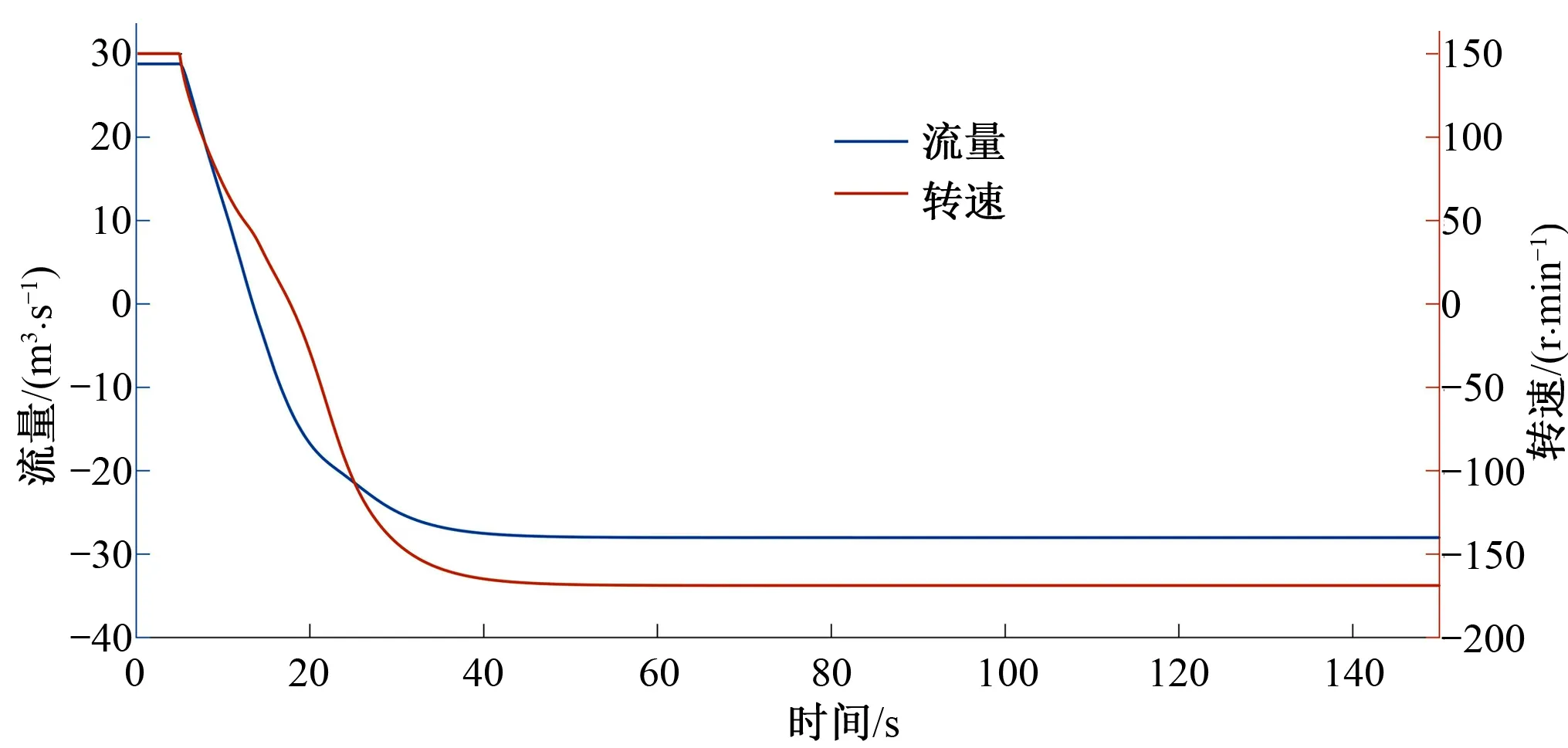
(a) 超駝峰0.5 m

由圖4(b)可以看出，當外江水位超駝峰1.0 m時，一旦泵發生事故停機，正向流量將開始逐漸減小，在12.5 s左右，流量變為0。此后泵進入制動工況，在重力作用下，水開始倒流，泵轉速迅速減小，16.4 s時，泵轉速降為0。之后機組在凈揚程作用下開始反轉，50 s左右，泵流量和轉速趨于穩定達到倒流最大值和倒轉最大值，此時，泵倒流流量為30 m3/s，是額定流量的1.25倍；倒轉轉速為180 r/min，為額定轉速的1.2倍。根據《泵站設計規范》[8]要求的“泵最高反轉速度不應超過額定轉速的1.2倍”，可確定在內河水位為24.59 m時，泵站外江極限超駝峰值應為1.0 m以下。

4.2 正常停泵，閘門兩階段關閉尋優

4.2.1 優化模型

(1)決策變量：取閘門的關閉程序參數[9](快關時間T1、快關行程H1、慢關時間T2，慢關行程H2)為決策變量，共4個。

(2)目標函數：在優化閘門的關閉程序時，總是希望在滿足約束條件的前提下，管線中出現的最大水錘壓力越小越好。因此，目標函數表示為：

(13)

式中：i為節點編號，i= 1，2，…，NS；Hmax(i)為各節點出現的最大水錘壓力；[Hmax](i)為各節點的管道允許最大壓力。

(3)約束條件：閘門關閉程序優化的約束條件包括系統約束、水泵倒轉轉速和倒轉時間約束、閘門關閉時間約束、決策變量上下限約束。①系統約束：瞬變流水錘基本微分方程、系統上下游邊界條件、泵端邊界條件、閘門端邊界條件。②水泵倒轉轉速和倒轉時間約束：水泵倒轉轉速不應超過額定轉速的1.2 倍，超過額定轉速的持續時間不應超過2 min。 ③閘門關閉時間約束：閘門關閉總時間不應超過允許的最大時間，為減少水量倒泄，本次計算取為120 s；快關速度應大于慢關速度。④決策變量上下限約束：取閘門快關行程H1=2.0～3.5 m，慢關時間T2=(4-12)T1。

4.2.2 優化結果

采用遺傳算法對優化模型進行求解，得到快速閘門的最優關閉程序為10 s快關總行程的62.5%，90 s慢關余下的37.5%。

圖5為采用此關閉程序，外江水位分別在超駝峰0.5 m、1.0 m及1.5 m情況下泵轉速和流量隨時間的變化曲線，與圖4相比其最大倒瀉流量以及最大倒轉轉速的值都得到了明顯改善。從圖5(c)可以看出，最大倒瀉流量以及最大倒轉轉速出現的時間非常接近，大約在30 s左右。其中，最大倒瀉流量為20.8 m3/s，最大倒轉轉速為125 r/min。

5 結 語

考慮到特征線法在求解低揚程軸流泵的過渡過程中，誤差通常較大，為此本文基于剛性水錘和水泵全特性理論，建立了數學模型，該數學模型可廣泛應用于采用虹吸式出水流道的軸流泵機組。結合具體工程實例，并借助Matlab編程對該軸流泵站的過渡過程進行了數值計算。在軸流泵啟動過程中，分析了出水閘門在不同時間開啟下其對系統參數的影響。計算結果表明，為保證機組不發生超載，閘門的開啟時間不應超過60 s。

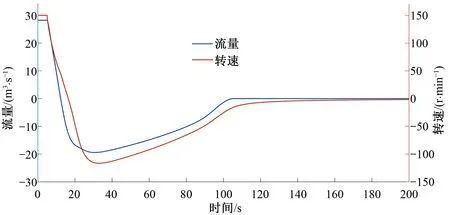
(b) 超駝峰1.0 m

通過事故停機(閘門、真空破壞閥均拒動的情況下)過渡過程計算，確定了外江極限運行水位超過駝峰底部高程的值應小于1 m，即外江水位在28.7 m以下時，泵站方可開機運行。

采用閘門兩階段關閉過程，選取閘門快關時間、慢關行程為決策變量，以使管線最大水錘壓力最低為目標函數并加以約束條件，建立了閘門兩階段關閉的優化模型。利用遺傳算法加以求解，得到了最優關閉過程為10 s快關總行程的62.5%，90 s慢關余下的37.5%。