空陸攻防博弈的動態武器目標分配*

張先劍

(國防科技大學 智能科學學院, 湖南 長沙 410073)

武器目標分配是現代大規模攻防作戰的核心問題，它的最終目的是期望通過最優的武器目標分配方案，充分發揮武器系統的整體效能，以實現攻防作戰的最佳結局。傳統研究主要利用動態規劃算法、粒子群優化、蟻群優化、類電磁算法等方法解決靜態或動態武器目標分配問題，但大部分研究[1-8]均把目標設想為無智慧、無對抗能力的被動防御對象，單一從己方角度考慮武器目標分配問題，忽略對手的策略和利益，沒有充分考慮實戰中的動態博弈特征——作戰雙方行動和策略的關聯性。攻擊與防御是互相對立的雙方，共存于博弈的統一體中，相互制約、相互激勵，沒有考慮對抗雙方動態博弈特性的攻防決策難以應用于實戰。具體到武器目標分配問題研究，必須同時兼顧作戰雙方的戰術策略[9-10]、效能指標等重要因素，這正是使用博弈論方法的優勢之處。

針對動態武器目標分配問題，本研究將重點聚焦對抗建模，構建了基于雙方動態博弈的綜合數學模型，并利用納什均衡和帕累托最優算法進行求解。

1 基于納什均衡的武器目標分配

1.1 雙方博弈

博弈中競技者(決策主體)都是理性的，在選擇決策的時候都有著明確的“使自己的利益最大化”的目標。博弈論就是專門研究博弈現象中各方是否存在最合理的行動方案，以及如何找到合理的行動方案即均衡解的數學理論和方法。而這里的均衡解，就是一個能夠得以維持的結果，或者說是所有競技者不得不接受而又不可能更好的結果[11]。

定義1博弈可以描述為式(1)所示數學形式[12]。

Γ=[N,P,{SK},J,{J(xK)}]

(1)

式中：N為任意的競技者集合；P為聯合組織(機構)的集合；K表示具有共同行動和利益的競技者小組；SK為聯合K∈P的任意策略集合；J為在P上的所有博弈結果的任意集合；J(xK)為如果聯合K采取策略xK，那么在P上可能的結果集合。

一般情況下，博弈可以簡化為包含競技者、策略和盈利(損失)函數的表達形式。

Γ=[N,S,J]

(2)

式中，N=[1,2,…,n]，S=[S1,S2,…,Sn]，J=[J1,J2,…,Jn]。

定義2策略qr=(qr,1,…,qr,mk)是指標函數J的納什均衡解，如果對于任意的qi∈Si,有

(3)

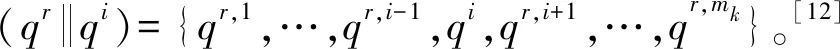
1.2 武器目標分配模型

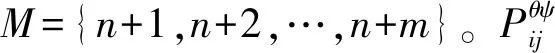
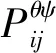
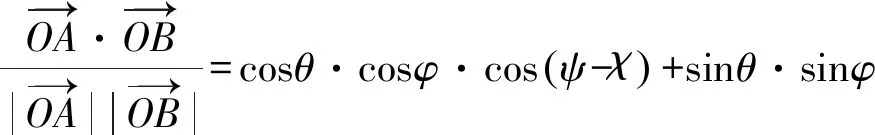
并且有

考慮距離因素，如

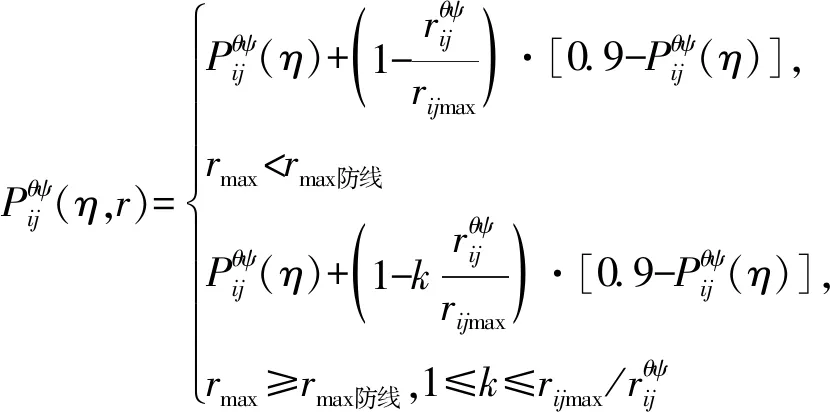
(4)

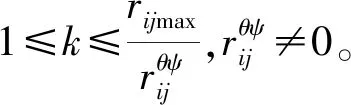
那么，被擊中的第j類目標平均數量為：

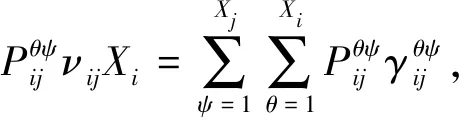
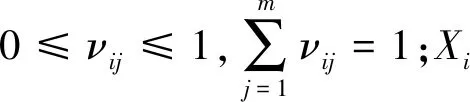
(5)

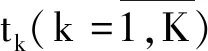
(6)

式中，tk-1→tk為多個導彈發射裝置單次齊射周期。

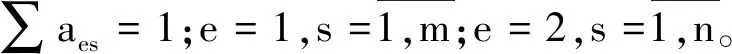
那么目標損失函數可以表示為：

Je(ν)=∑aesJes

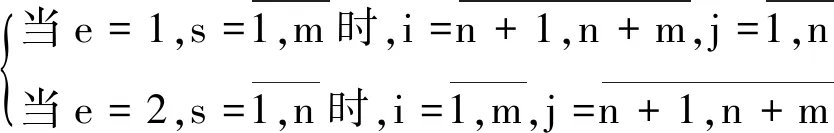
其中，索引i，j分別代表主動武器和被動目標。

損失函數有這樣的思想，即每一方都期望敵方主、被動目標最終數量最小，而使己方主、被動目標數量最大化，并且通過權重系數控制敵方主動武器數量的衰減速度。那么有J甲→min，J乙→min。

1.3 武器目標動態分配算法

使用納什均衡的武器目標分配算法共分四個階段：在第一階段獲取作戰雙方的目標信息，如數量、速度、距離、飛近時間、方位等；在第二階段根據目標信息和命中率函數計算命中率；在第三階段構建策略空間和策略收益；在第四階段尋找最優策略。

1.3.1 獲取作戰雙方武器目標信息

在作戰期間，偵察預警探測系統全天候實時監測各種飛行目標，并獲得如出發位置、數量、速度、距離、實時空間位置、方位等信息，對獲取的敵方信息進行鑒別，如判斷是否佯攻、使用欺騙手段和制造假象等。分析敵方作戰行動意圖、策略和可能攻擊目標區域。

在獲取目標信息后，可以利用層次分析法(Analytic Hierarchy Process, AHP)等方法根據目標速度、高度、距離和方位角等因素進行多因素綜合威脅排序。

1.3.2 計算命中率

基于1.2節中獲得的距離、方位等信息，根據式(4)計算命中率。在計算命中率時，還應綜合考慮電子對抗環境對于導彈命中率的影響，比如地面防御系統電子干擾裝置會對空襲目標的命中率產生直接積極影響，也可能會對己方攔截導彈產生微弱消極影響。電子對抗影響因素主要跟電子干擾裝置的功率有關。

Pij=Pijmax·e-μi·λd·e-μj·λk

(7)

1.3.3 構建策略空間和策略收益

策略空間與控制參數的數量和取值步長有關，設步長為l，控制參數νij數量為q，則單次齊射目標分配策略空間數為(1/l)q。

1.3.4 尋找最優策略

首先獲得所有符合策略收益的策略解集合，然后根據納什均衡解定義，在有效解的集合中選取符合作戰雙方目標損失函數的均衡解。在均衡解的選取過程中應注意，納什均衡解可能有一個或多個，此時應根據極大極小原理進行篩選(基于最壞情況考慮，爭取最好的結果)。

2 實例分析

2.1 基本想定

作戰想定：攻擊方首先使用陸、海、空平臺發射若干戰術導彈打擊防御方地面防御系統，企圖癱瘓或消滅防御方防空力量，然后指派戰斗機編隊護航轟炸機編隊對防御方重要目標實施打擊。防御方實施分層分段攔截，轟炸機的威脅指數最高，戰術導彈其次。

所研究的目標動態分配是指在連續動態作戰中不同階段的目標分配，階段劃分是由地面攔截導彈的射程決定的，比如首先是遠程攔截，而后進行中近程攔截(如圖1所示)。

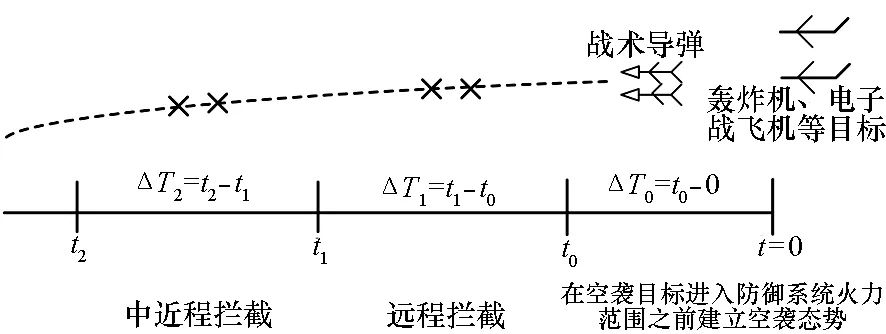
圖1 階段劃分示意圖Fig.1 Illustration of stage division

2.2 模型構建

設甲乙兩方參與攻防作戰，甲方為空襲系統，組成包括轟炸機、導彈、戰斗機和電子戰飛機；乙方為地面防御系統，組成包括導彈發射裝置、雷達站、電子對抗裝置和指令站等。

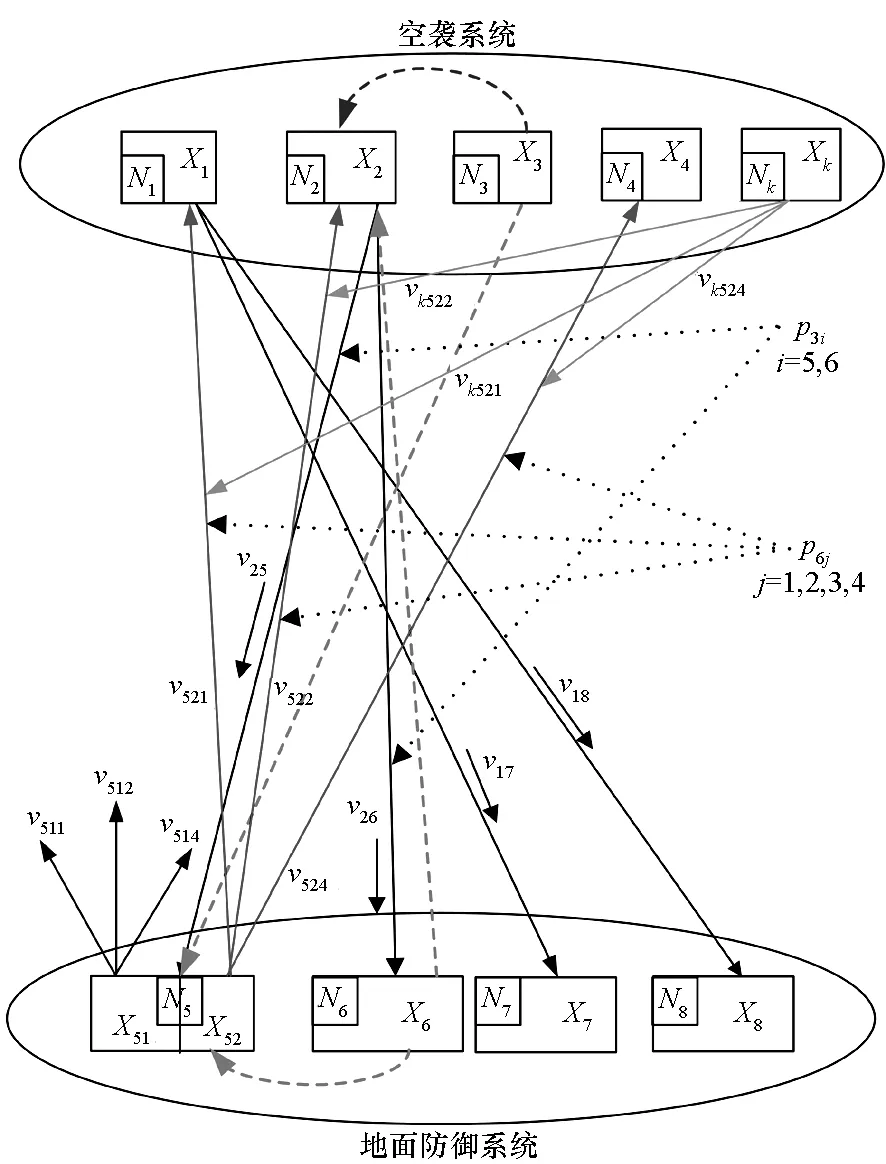
圖2 甲乙雙方對抗關系示意圖Fig.2 Illustration of A-B counters relationship

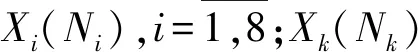
首輪(遠程攔截防御階段)雙方對抗過程如圖3所示，空襲系統首先發射導彈打擊地面防御系統，防御系統遠程導彈實施攔截打擊。

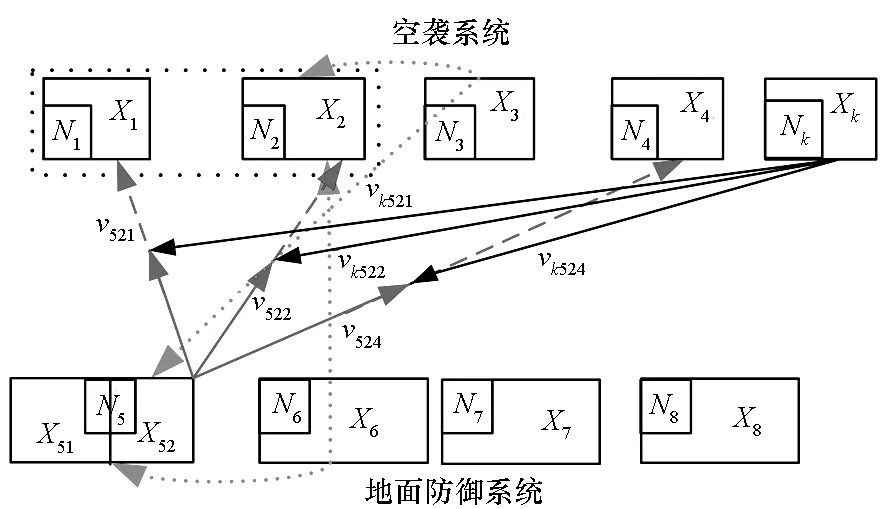
圖3 首輪甲乙雙方對抗關系示意圖Fig.3 Illustration of A-B counters relationship in the first round

綜合數學模型有:

(8)

(9)

次輪(中程攔截防御階段)雙方對抗過程如圖4所示，首輪攔截打擊之后，由中近程導彈負責對成功突防的導彈和轟炸機進行攔截。

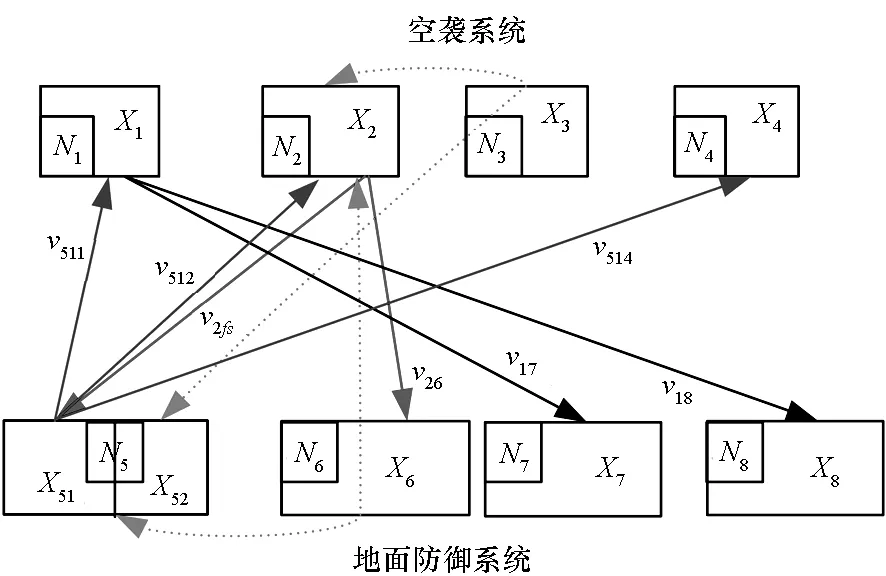
圖4 次輪甲乙雙方對抗關系示意圖Fig.4 Illustration of A-B counters relationship in the second round

綜合數學模型有：

(10)

(11)

2.3 實驗分析

假設初始條件如下：X1=14,X2=14,X3=12，X4=14,X5=8,X51=24,X52=32,X6=2,X7=4,X8=2；a11=0.25,a12=0.25,a13=0.45,a14=0.05,a21=0.35,a22=0.35,a23=0.25,a24=0.05,Р521=0.5,P522=0.5,P524=0.5,P3521=0.5,P3522=0.5,P3524=0.5。

首輪對抗結果如表1～3所示。

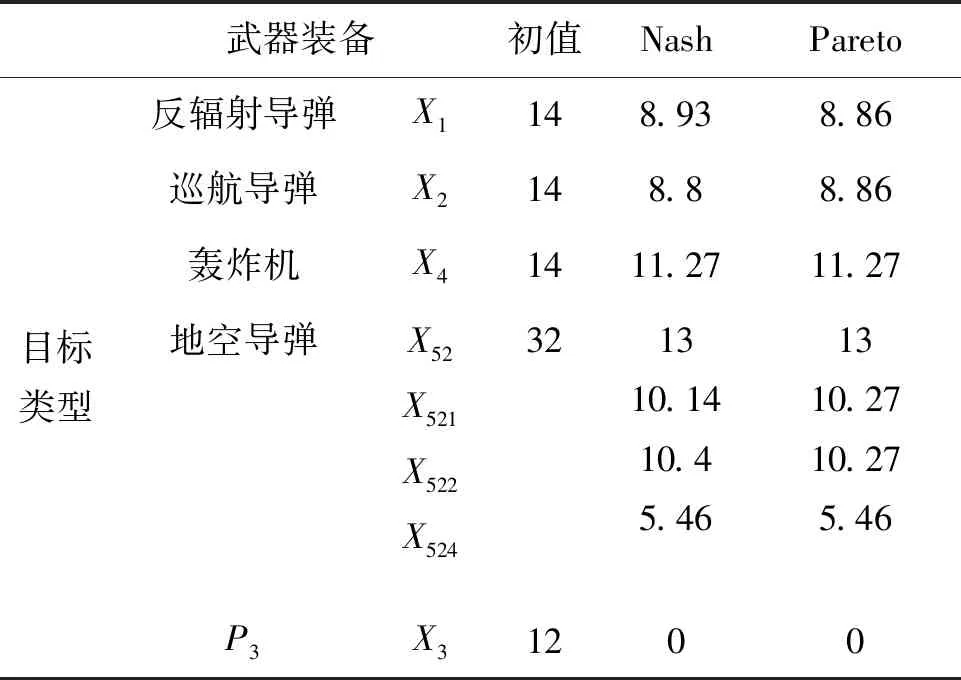
表1 首輪對抗后數量變化

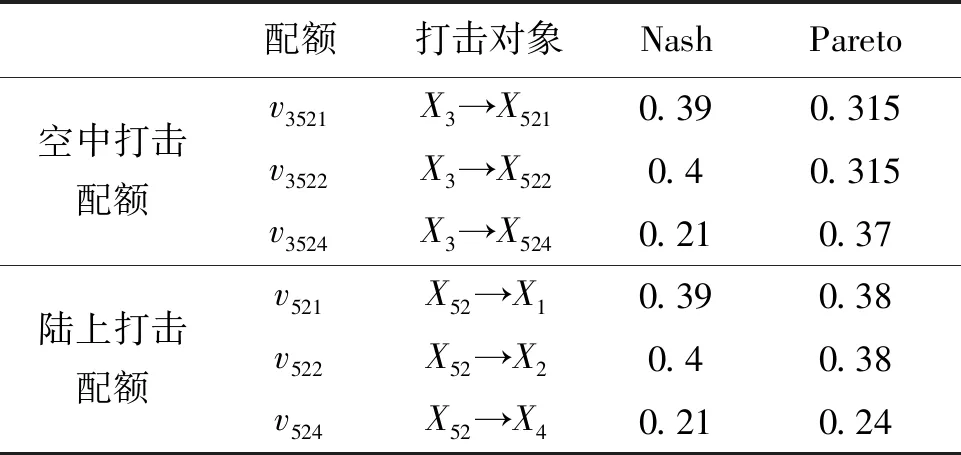
表2 首輪打擊配額

表3 首次對抗損失和收益

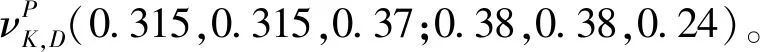
次輪對抗結果如表4～6所示。

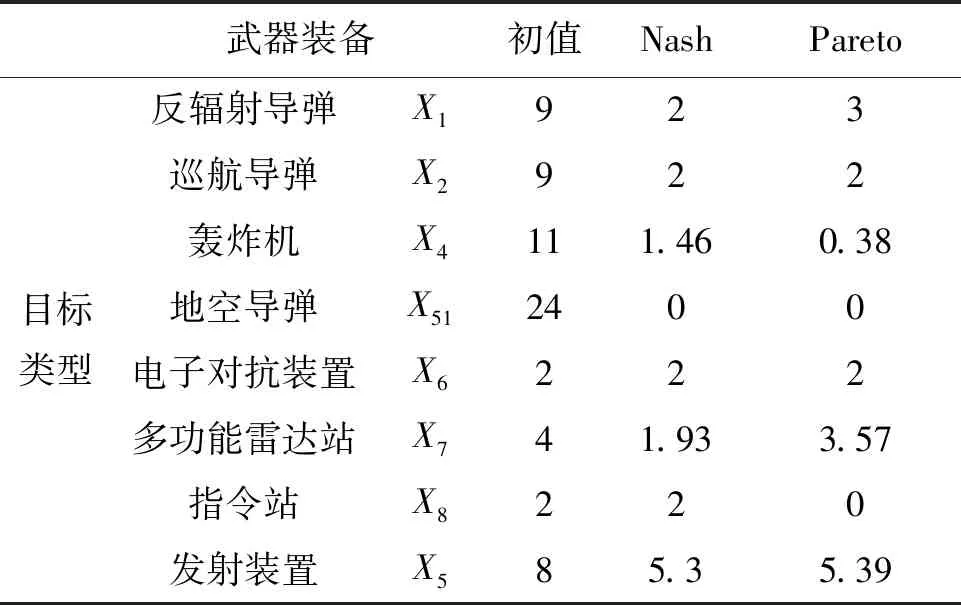
表4 次輪對抗后數量變化

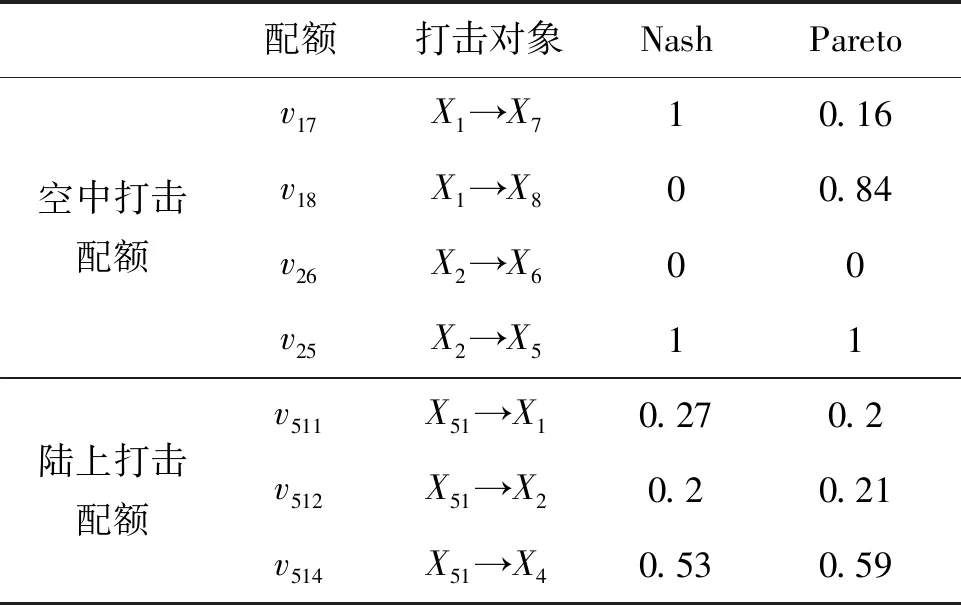
表5 次輪打擊配額

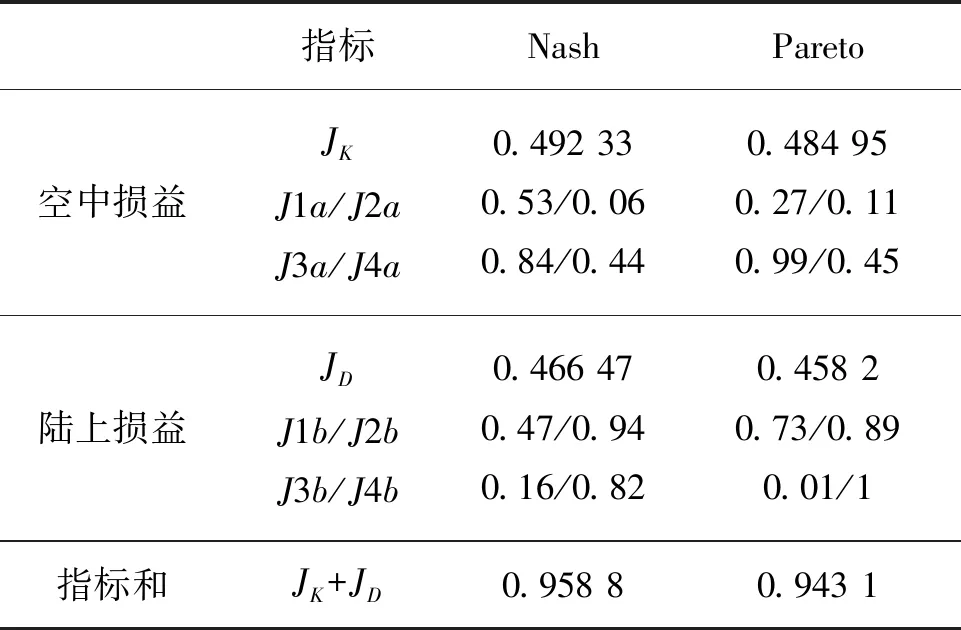
表6 次輪對抗損失和收益

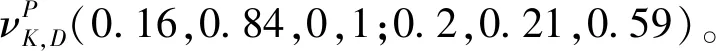
3 結論

本文指出了國內現有針對武器目標分配問題研究的優勢和不足之處，重點闡述使用基于雙方動態博弈的思想解決大規模作戰武器目標分配問題的科學性和合理性，構建了基于雙方博弈的攻防對抗綜合數學模型，并以實例證明使用納什均衡、帕累托最優方法可以有效解決動態武器-目標分配問題。

1)基于博弈論方法綜合考慮作戰雙方的策略和行動方案，保證了決策方案在實戰應用中的科學有效性。

2)提出新穎的建模思維，通過引入狀態變量、控制參數和權重系數來構建策略空間和策略收益，對武器目標分配問題進行了求解，獲得了作戰雙方各自最優戰術策略。