連鑄板坯鼓肚有限元分析
章裕琳,石林波,何保衛
(1.中國重型機械研究院股份公司,陜西 西安 710000;2. 廣西盛隆冶金有限公司,廣西 防城港 538000)
0 前言
鼓肚指鑄坯在凝固過程中,在鋼水靜壓力作用下,凝固殼上產生的向外鼓脹成凸面的現象。鼓肚會加重中間偏析和內部裂紋等缺陷,若不加以控制,嚴重將會導致漏鋼。因此,連鑄板坯的鼓肚變形分析對于連鑄機的設計和實際生產具有重要的意義[1-4]。
本文建立了板坯連鑄凝固傳熱的有限元模型,應用ANSYS有限元軟件,采用二維“切片法”[5-6],得出任意時刻任意位置板坯切面的溫度場。在此基礎之上,把凝固仿真得到的溫度場作為初始條件,建立了鼓肚變形三維有限元模型,研究了板坯的鼓肚變形規律,分析了主要工藝參數對鼓肚的影響,為連鑄機的設計和實際生產中工藝參數的選定提供一定的參考。
1 板坯連鑄凝固傳熱的有限元分析
以某鋼廠直弧形板坯連鑄機為研究對象,鑄坯斷面1000 mm×230 mm,鋼種為Q235,拉速為1.5 m/min,結晶器高度為900 mm。
在對連鑄過程進行合理假設基礎上,對傳熱微分方程和邊界條件進行簡化,將鑄坯傳熱簡化為二維傳熱問題[7-10],建立了板坯凝固傳熱的有限元模型,如圖1所示。本研究用時間來控制邊界條件的施加,截面在結晶器、二冷區、空冷區施加不同的邊界條件[11-15],用非穩態的計算方法來模擬鑄坯的這個穩態過程。
圖1 板坯凝固傳熱有限元模型
通過對ANSYS結果數據的后處理,得到鑄坯寬面中心坯殼厚度隨距離彎月面距離的曲線,如圖2所示。
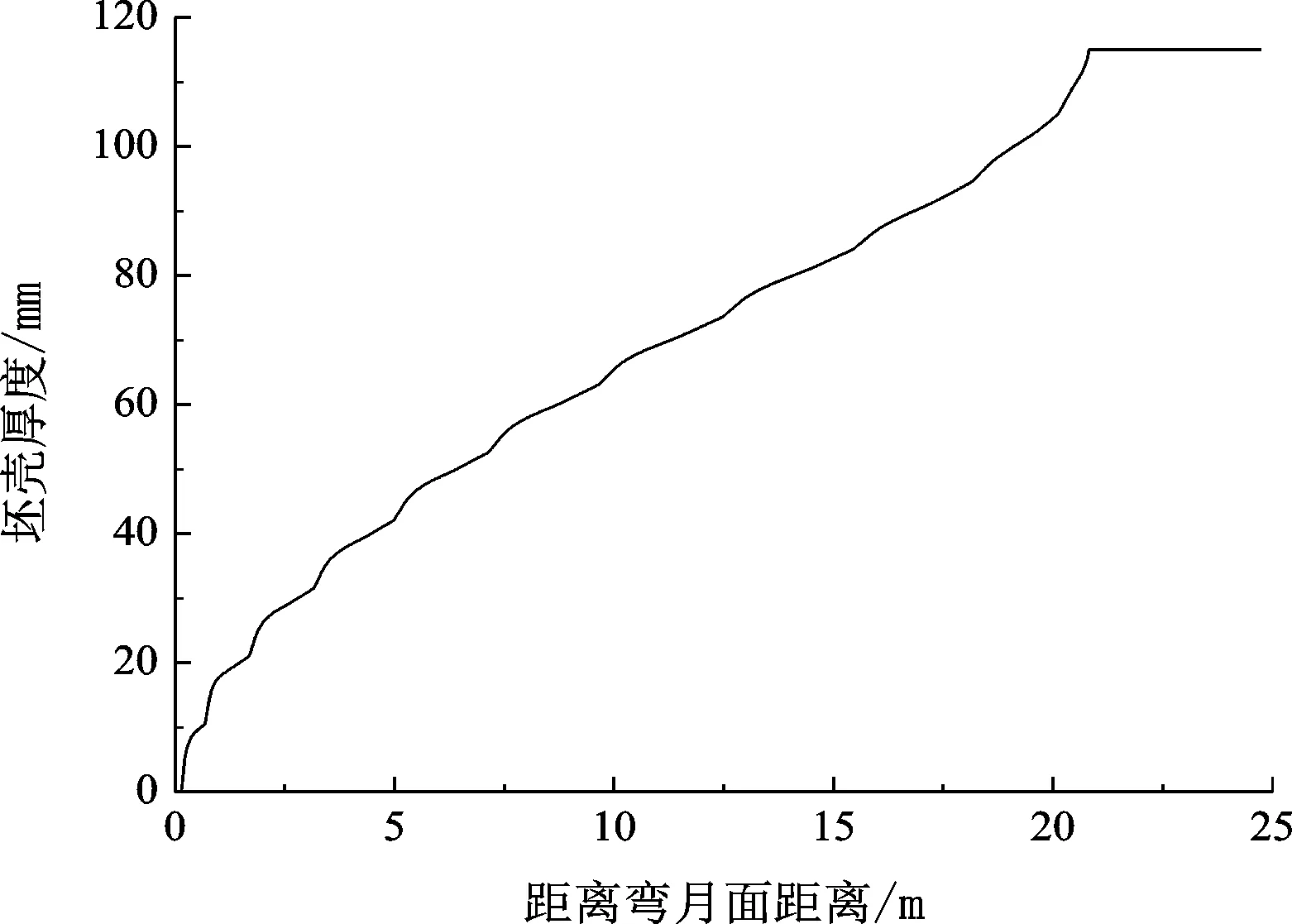
圖2 鑄坯凝固狀態圖
2 板坯連鑄凝固鼓肚變形有限元分析
為簡化計算,建模做如下假設和簡化:
(1)鑄坯溫度只考慮厚度方向的變化;
(2)鋼的高溫力學性能僅是溫度的函數;
(3)把液芯簡化為空腔,鋼水靜壓力作用于空腔內壁;
(4)考慮到結構和邊界條件的對稱性,取兩輥間鑄坯的1/4建模;
(5)以寬面中心的坯殼厚度作為鼓肚模型的坯殼厚度;
(6)輥子為剛體。
板坯連鑄鼓肚有限元模型如圖3所示。鼓肚一般出現在坯殼厚度較薄處,本文以直線段最后一對輥子間的鑄坯為研究對象。輥距為240 mm,輥徑為200 mm,坯殼厚度為25 mm。

圖3 鼓肚變形有限元模型
3 連鑄板坯三維鼓肚仿真結果及分析
3.1 鼓肚變形量
圖4、圖5所示的是板坯的X向和Y向鼓肚變形量云圖,由圖4、圖5可以得出:板坯X向和Y向最大鼓肚變形量分別為0.03 mm和0.4 mm,且在鑄坯窄面和寬面中心處。

圖4 鼓肚X向變形

圖5 鼓肚Y向變形
模擬結果與采用經驗公式[16]計算的結果基本一致。
以Y向鼓肚變形最大點為分析對象,研究其Y向的等效應力、鼓肚變形量與時間的關系,如圖6、圖7所示。
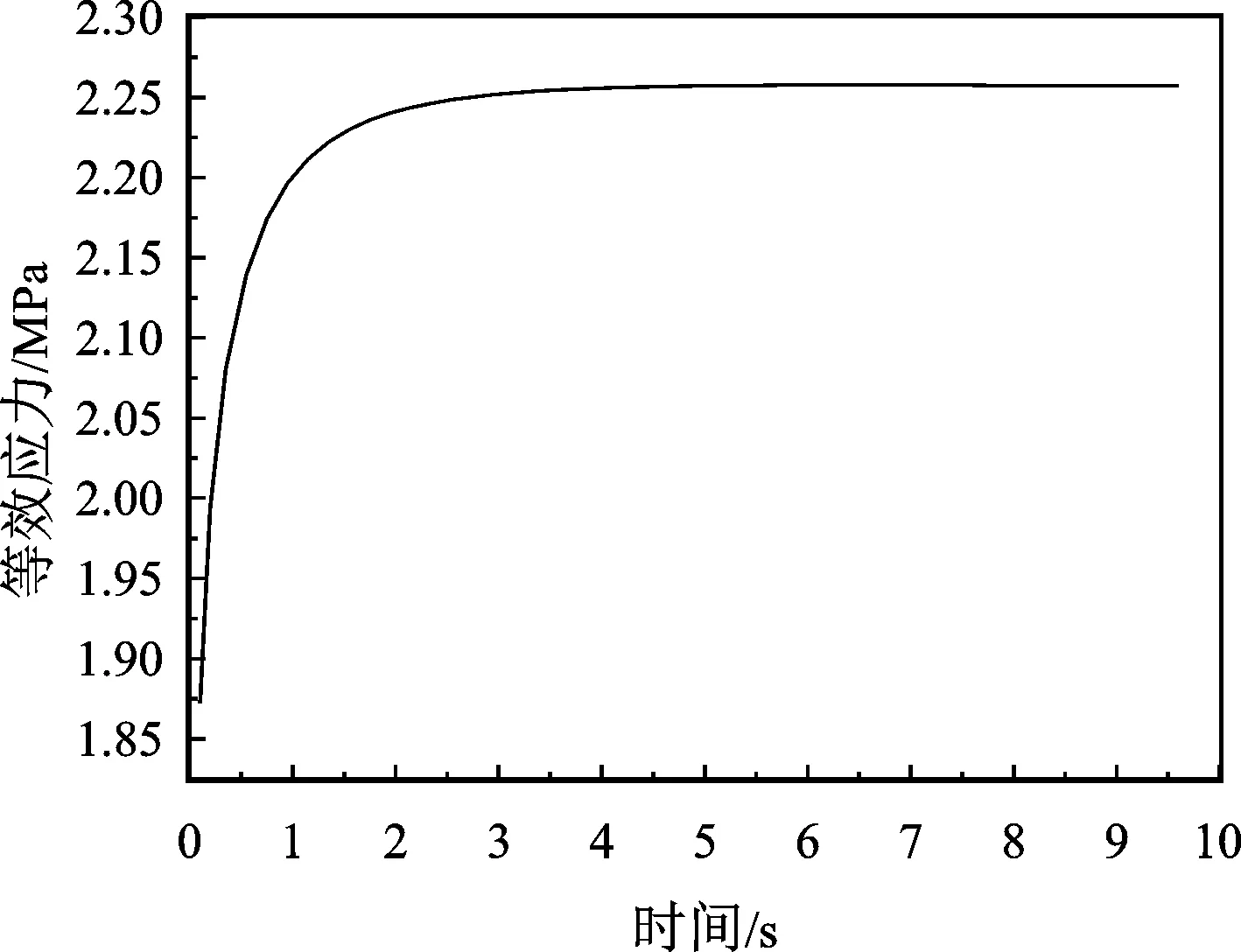
圖6 等效應力與時間關系

圖7 Y向鼓肚與時間關系
由圖6可得,該點的最大等效應力為2.3 MPa,小于該點的屈服應力5 MPa[17],因此該點在彈性變形階段。
由圖7可得,彈性變形和高溫蠕變引起的鼓肚量分別為0.1 mm、0.31 mm。因此,鼓肚變形主要是由高溫蠕變引起的,這與文獻[18-19]運用解析法得到的結論是吻合的。
3.2 主要參數對鼓肚的影響
影響鼓肚變形的因素很多,主要有澆鑄速度、輥徑、輥距、鋼水靜壓力等,本文重點探討澆鑄速度和輥距對鼓肚的影響。
3.2.1 輥距對鼓肚的影響
在拉速為1.5 m/min,澆鑄溫度為1542 ℃的條件下,以固液分界面上寬面對稱中心點為研究對象,改變輥距,分別模擬了輥距為280 mm、260 mm、240 mm時的鼓肚變形,如圖8所示。其中Z為拉坯速度方向的坐標,L為輥距。
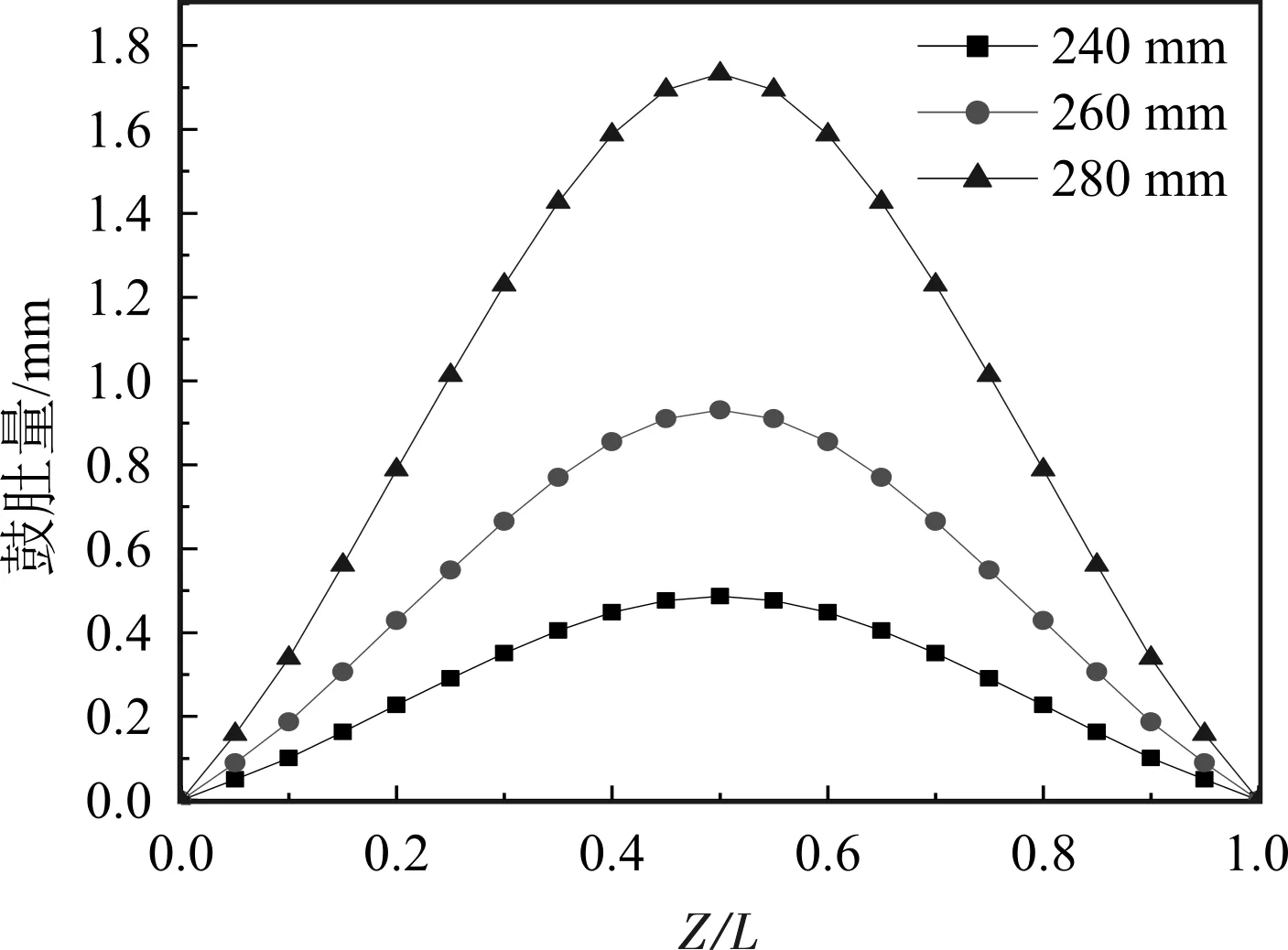
圖8 輥距對鼓肚的影響
由圖8可看出,輥距對鼓肚的影響十分明顯。當輥距由280 mm變為240 mm,最大鼓肚量由1.7 mm減小到0.4 mm。因此,連鑄機設計多采用小輥距來防止鼓肚變形。
3.2.2 拉速對鼓肚的影響
在拉速為1.5 m/min,澆鑄溫度為1542 ℃的條件下,分別改變拉速為1.4 m/min、1.3 m/min,由凝固仿真可得到對應的鑄坯的表面溫度、坯殼厚度以及蠕變時間,如表1所示。
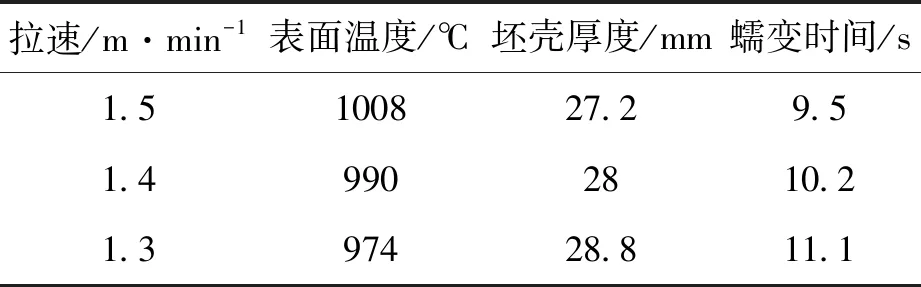
表1 不同拉速下的參數
圖9給出了拉速對鼓肚的影響。由圖9可以看出,拉速由1.3 m/min增加到1.5 m/min,最大鼓肚量由0.38 mm增大到0.42 mm。拉速提高,最大鼓肚變形量增大,但拉速對最大鼓肚量的影響不明顯。
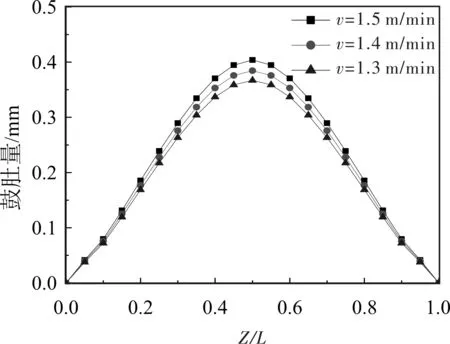
圖9 拉速對鼓肚的影響
因此,要有效控制鼓肚變形,必須設計合適的輥距,制定合理的工藝制度,匹配穩定的拉坯速度和鋼水過熱度[19-20]。
4 結論
(1)用“切片法”對板坯連鑄凝固過程進行了有限元仿真,得到了鑄坯的溫度場,進而得到了鑄坯的坯殼厚度;
(2)在板坯連鑄凝固仿真的基礎上,建立了鼓肚變形有限元模型,采用ANSYS隱式計算蠕變方程,得到了鑄坯鼓肚變形最大處都在寬面和窄面的中心處,且蠕變變形是引起鼓肚變形的主要因素,仿真結果與理論計算是相吻合的;
(3)分析了輥距和拉速對鼓肚的影響,為輥列設計和工藝參數的選擇提供了一定的參考。

