兩種Sobolev空間之間的嵌入范數

胡增周，王 薇，許貴橋

（1.河北省城鄉建設學校，石家莊 050031；2.天津師范大學 數學科學學院，天津 300387）

1 引言與預備知識

求函數空間上數值問題的滿足一定精度的解所必須搜集的最小信息量，是信息復雜度理論研究的核心問題，其中易處理性問題是目前的研究熱點[1-5].當前研究最多的是基于單變量第二類Sobolev空間與第一類Sobolev空間的多元問題的易處理性，而不同函數空間之間的嵌入范數是研究多元問題易處理性的主要工具[6-10].設

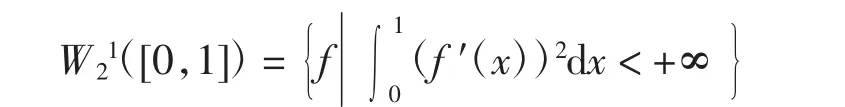
且f是局部絕對連續的.在W21（[0，1]）上引入第一類Sobolev空間H1，其相應的范數為

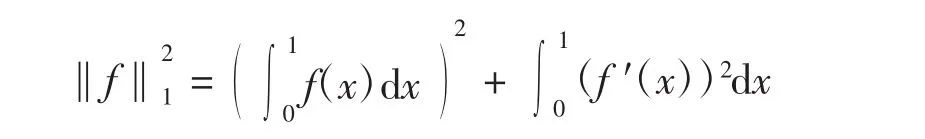
同時，在W21（[0，1]）上引入第二類Sobolev空間H2，其相應的范數為

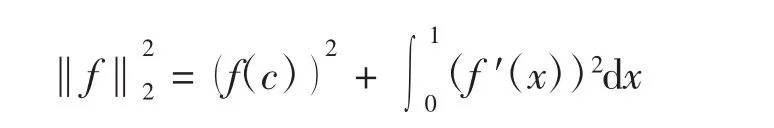
H2稱為以c∈[0，1]為錨的Sobolev空間，其中c稱為錨.顯然，H1與H2之間是互相嵌入的，文獻[8]對于錨取端點（即c=0）的H1與H2的嵌入范數做了研究，得到了嵌入范數的準確值，而在許多研究如文獻[9，11-13]中，c的值都是任意的，本文對任意c∈[0，1]，得到了嵌入范數的準確值.

2 主要結論

首先引入2種空間之間嵌入的定義.記

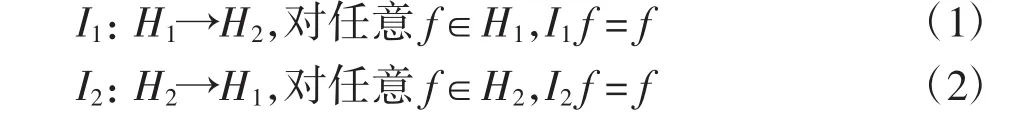
下面引入算子范數的定義.設F、G為2個線性賦范空間，若算子I：F→G為一個線性有界算子，則線性算子I的范數為

定理設I1、I2定義如式（1）和式（2），則

其中∈[0，1].

證明先計算‖I1‖H1→H2.記F=W21（[0,1]）.由定義知

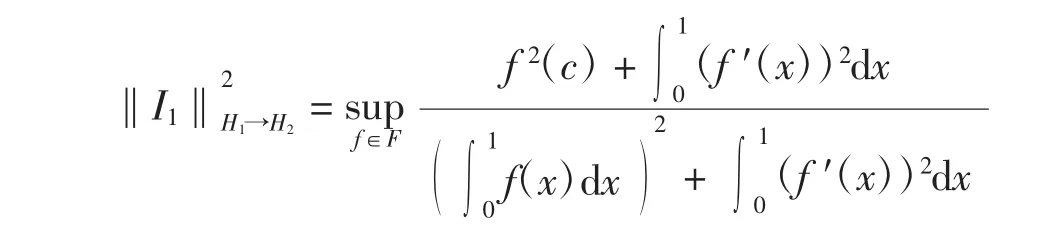
對f（x）做余弦展開得

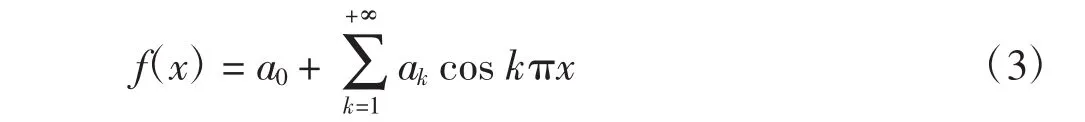
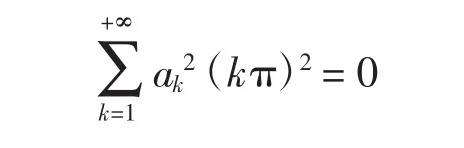
由此可得

由式（3）和式（4）得

因此有

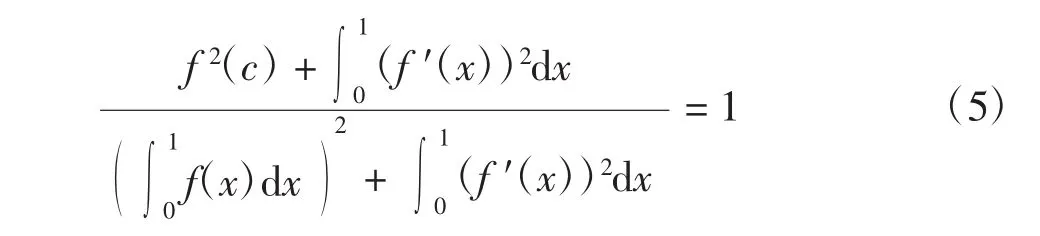
由式（3）和式（6）以及Cauchy-Schwarz不等式可得

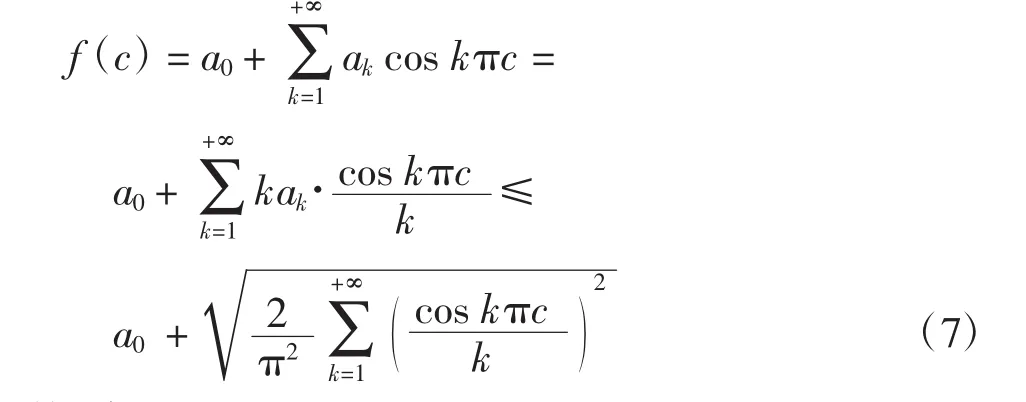
另外，令

則ak滿足且有

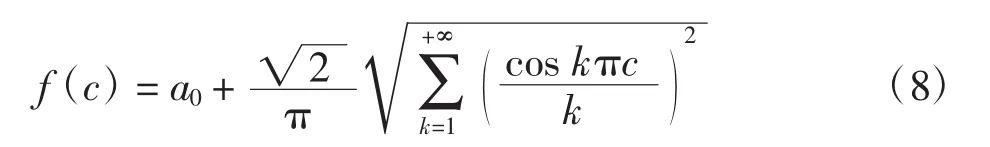
將f（x）=（x-1）2在（0，1）上展開成余弦級數，有

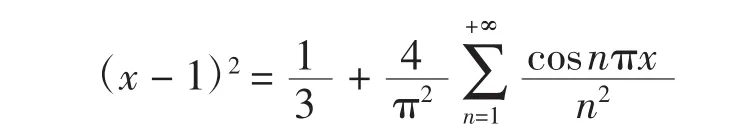
令x=2c，則有

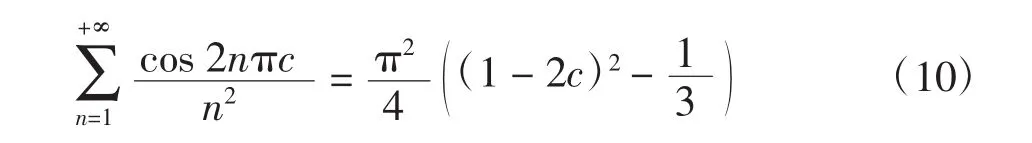
將式（10）代入式（9）得

由式（7）、式（8）和式（11）可得

對固定的a0，記其為a，則有

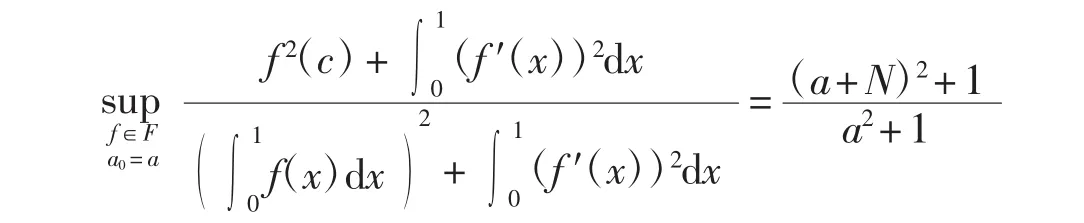
因此

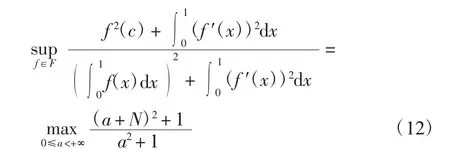
令

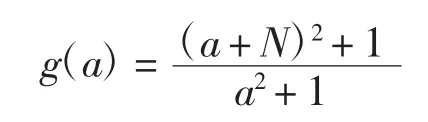
對g（a）關于a求導，可得g（a）當a=時取得最大值，且其最大值為

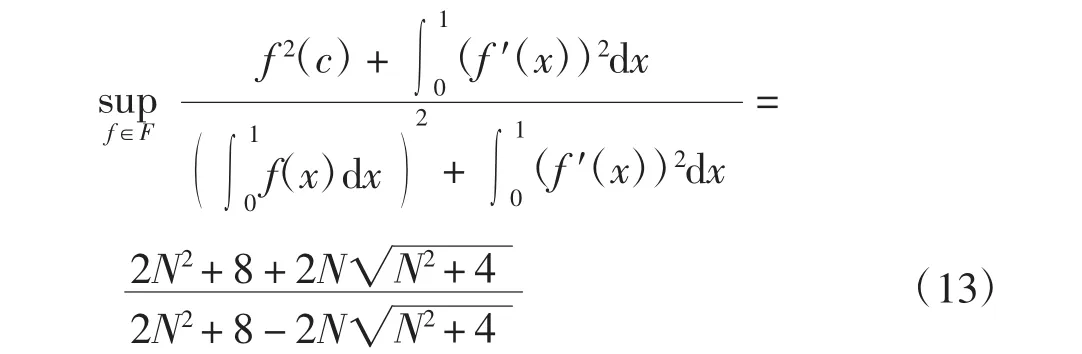
下面計算

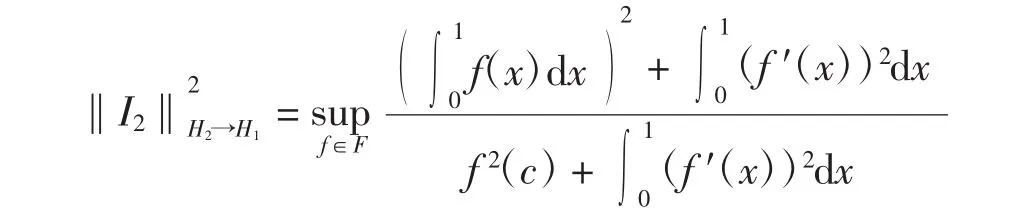
其中c∈[0，1].如果則f′（x）幾乎處處為0，即f（x）=a，a為常數，則顯然有

對式（14）兩邊同時積分得

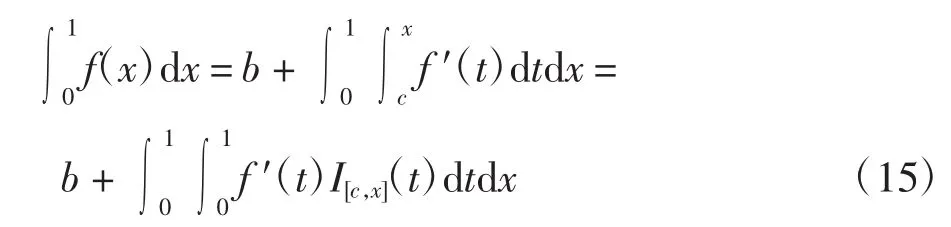
由Fubini積分交換定理得

由Cauchy-Schwarz不等式可得

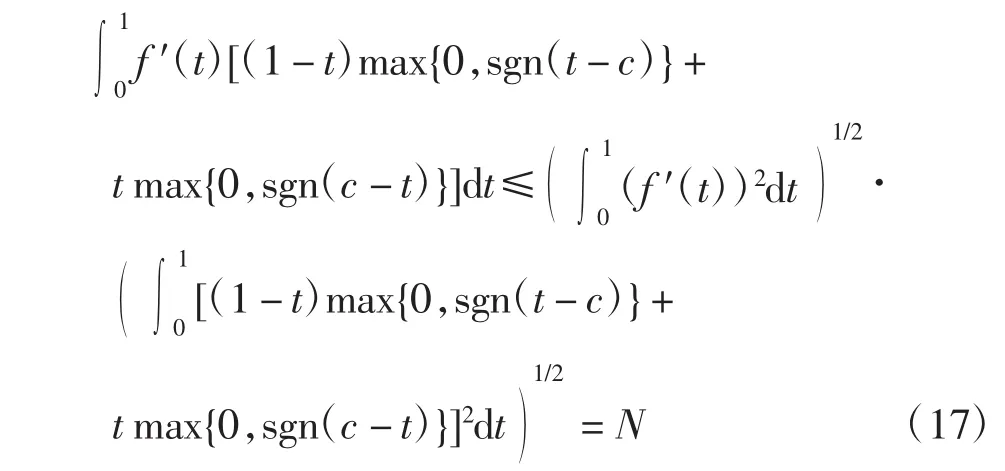
由式（16）和式（17）可得

此外，令

則f（x）同時滿足由此結合式（18）可得

由式（19）得

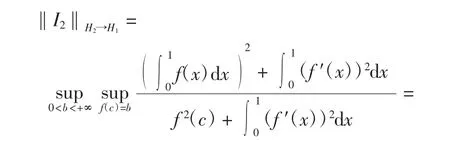
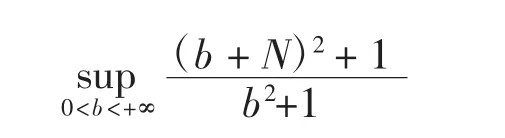
注：當c=0時，由式（13）得

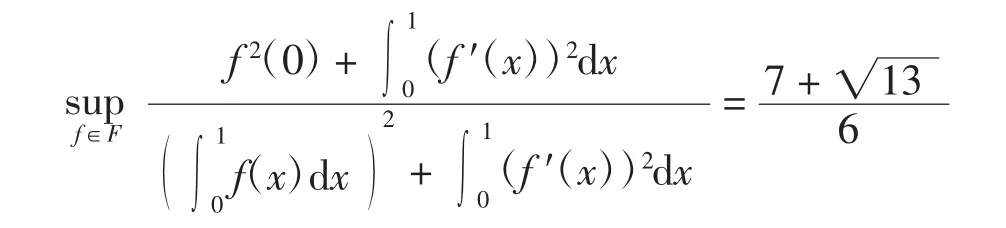
文獻[8]給出了上面的等式成立，但沒有給出具體的證明，本文證明了文獻[8]的結論，并對任意c∈[0，1]給出了該嵌入范數的具體值.