Mg在Si（220）表面吸附的第一性原理計算

蘇 蓉，李 娜，張佳佳，李曉琴，趙 輝

（天津師范大學 物理與材料科學學院，天津 300387）

幾乎所有金屬都能與Si表面發生反應生成硅化物，而金屬/硅化物體系不僅被廣泛應用于工業目的，同時具有重要的科研價值[1].其中，堿金屬和堿土金屬在硅表面的吸附引起了研究人員的特別關注，尤其是在Si表面吸附Mg原子[2].將Mg原子吸附到Si襯底上可以生長出Mg2Si薄膜.Mg2Si是一種重要的帶隙半導體，在光電子領域具有潛在的應用價值.此外，Mg2Si是一種無毒、無污染的材料[3]，其組成元素Mg和Si在地球上的含量豐富，資源壽命長，是一種環境友好型半導體.

實驗研究方面，國內外研究人員采用不同的實驗方法和手段將Mg原子沉積在Si表面上[4]制備Mg2Si薄膜.Hosono等[5]通過在Mg蒸汽下加熱塊狀Si（111）獲得了晶向為（211）的多晶Mg2Si薄膜.Mahan等[6]通過分子外延技術在200℃下將Mg沉積在Si（111）基底上獲得了具有（111）晶向的多晶Mg2Si薄膜.Yang等[7]基于放電等離子燒結法利用Mg和Si粉末制備了Mg2Si塊體.Wittmer等[8]利用脈沖激光退火沉積技術將Mg沉積在Si（111）襯底上制備得到Mg2Si薄膜.

目前，有關Mg在Si晶面吸附的理論研究相對較少，Ying等[9]利用第一性原理對不同覆蓋度（1/4，1/2和1 ML）下Si（111）表面吸附Mg原子的過程進行研究，揭示了Mg原子在Si表面的吸附機制.本研究采用基于密度泛函理論（DFT）的第一性原理方法構建了Mg在Si（220）表面的吸附模型，通過計算對其結構的穩定性和吸附特性進行分析，以期為在Si（220）襯底上沉積Mg制備Mg2Si薄膜提供理論依據.

1 計算模型與方法

為了研究Mg原子與Si（220）表面的相互作用，采用基于密度泛函理論的第一性原理研究該體系的電子結構.采用Material studio 6.0軟件包中的CASTEP（cambridge sequential total energy package）模塊進行計算.CASTEP是基于密度泛函理論的平面波贗勢方法的量子力學程序.計算中，選用廣義梯度近似（GGA）下的PW91泛函描述電子間的交換相關能，采用Mokhorst-Pack方法對K點進行取樣.平面波截止能設定為230 eV，不可約布里淵區的K點取樣為3×3×1，體系中各原子核內層電子與外層電子間的庫侖吸引勢采用超軟贗勢（ultrasoft pseudo potential）.為了獲得穩定結構，采用BFGS方法對未計算模型進行幾何優化.在進行自洽計算時，原子總能收斂值取為2×10-5eV/atom，設置平均原子力小于0.5 eV/nm，最大原子位移容差小于0.02 nm.Mg原子和Si原子的原子軌道分別為2p63s2和3s23p2.

為了測試贗勢平面波計算的可靠性，對于原始Si晶胞，使用7×7×7的K點網格和450 eV的平面波截止能進行收斂測試.優化后的晶格參數a0=0.549 5 nm，彈性模量B0=87.22GPa.計算結果與實驗值（a0=0.5430 nm，B0=98.80 GPa）吻合良好[10].在優化好的晶胞上建立Si（220）表面結構，再將Si（220）表面構建成2×2×1的超胞結構，縱向采用7個Si原子層，在表層上方加1.2 nm真空層，建立基底模型，如圖1所示.圖1中綠色原子表示頂層硅原子，藍色原子表示其余6層的硅原子.然后再對該模型進行幾何優化，優化時允許所有原子進行馳豫.

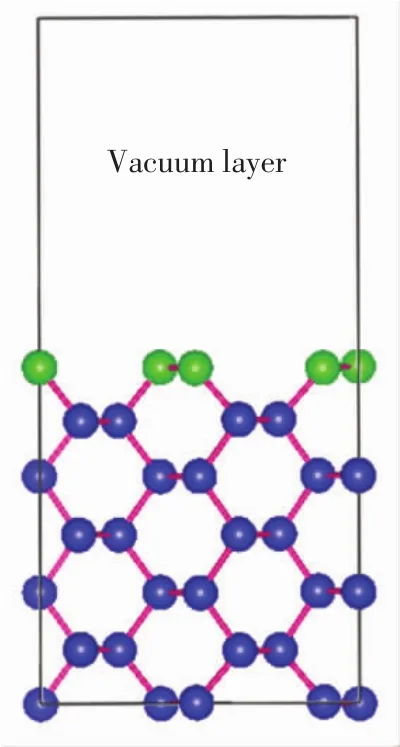
圖1 構造的Si(220)超胞表面主視圖Fig.1 Front view of the constructed Si（220）super cell surface

2 結果與討論

2.1 吸附能

固定優化后Si（220）基底模型最下方的4層原子，允許上面3層原子運動.然后把Mg原子吸附在基底模型表面，Mg原子在Si（220）表面有頂位（T）、橋位（B）和穴位（H）3種可能的吸附位置，如圖2所示.

圖2 吸附位置的俯視圖Fig.2 Vertical view of adsorption site

為了進一步確定Mg原子在Si（220）表面最穩定的吸附位置，本研究對Mg原子在Si（220）面上不同位置的吸附能進行計算，結果如表1所示.吸附能是把Mg原子從Si（220）表面分離所需要的能量，Ead=EMg/Si(220)–ESi(220)-EMg，其中EMg/Si(220)是吸附了Mg原子的Si（220）表面結構的總能，ESi(220)是未吸附Mg原子時Si（220）表面結構的能量，EMg為孤立Mg原子的能量.計算EMg的方法是在構造的邊長1nm的立方原胞中放置1個Mg原子，然后通過幾何優化求出.吸附能越低表明表面結構吸附原子的能力越強，最終獲得的吸附結構越穩定[11].

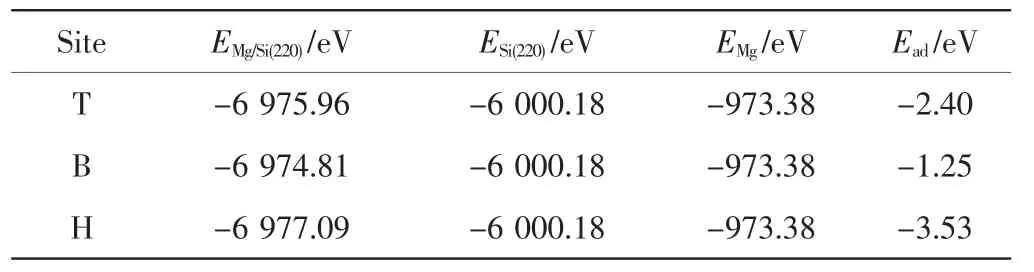
表1 Mg/Si表面體系優化后的能量Tab.1 Energies of Mg/Si surface system after optim ization

負值的吸附能表明吸附體系比未吸附體系更穩定，且數值越小，吸附的構型越穩定，所以通過比較吸附能的大小即可確定吸附的最優位置.由表1可知，Mg原子在Si（220）表面的頂位、橋位和穴位的吸附能均為負值，表明其吸附構型均可形成相對較穩定的結構.但對比吸附能的大小可知，Mg原子在穴位的吸附能小于橋位和頂位的吸附能，說明Mg原子在穴位比在橋位和頂位更容易被吸附[12].

2.2 吸附構型和功函數

Mg原子最初被放置在Si（220）表面頂位（T位）、橋位（B位）和穴位（H位）3個高對稱吸附點.吸附結構經過弛豫達到最小的能量結構，通過計算吸附能已知Mg原子優選吸附在Si（220）表面的穴位.進一步計算3種吸附結構Si—Si鍵和Mg—Si鍵的鍵長、吸附表面Mg原子的垂直高度（dh）以及它們的功函數，相應的計算結果如表2所示.

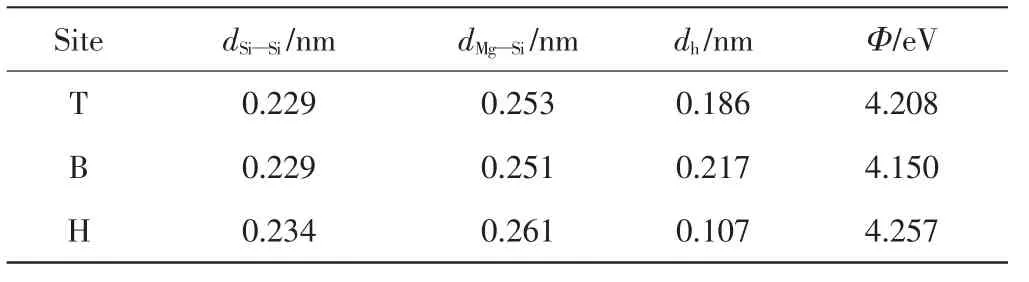
表2 鍵長dSi—Si和dMg—Si以及垂直距離dh和功函數ΦTab.2 Bond length dSi—Si and dMg—Si,the perpendicular distance dh and work functions Φ

由表2可知，通過比較吸附位點附近Si—Si鍵的鍵長，發現穴位（H位）的鍵長最長，且Mg原子與吸附位點相連的Mg—Si鍵的鍵長也是穴位（H位）的最長，說明穴位（H位）處的吸附形變最大.對于穴位吸附，吸附表面的Mg原子的垂直高度（dh）最低，說明此位點比頂位和橋位具有更強的吸附力.因此，Mg原子在Si（220）表面會優先吸附在穴位上.

半導體功函數是指真空中靜止電子與半導體費米能級的能量差.電荷發生轉移時，半導體的功函數發生變化[13].未吸附Mg原子的Si（220）表面的功函數為4.643 eV.由表2可知，頂位、橋位和穴位的功函數均小于理想Si（220）表面的功函數.功函數變小說明有電荷從Mg轉移到Si（220）表面.

2.3 電荷布居

通過電荷布居分析可以定量討論電荷的轉移情況，本研究對以上3種吸附結構的Mg原子與最鄰近Si原子的電荷布居進行分析，結果如表3所示.

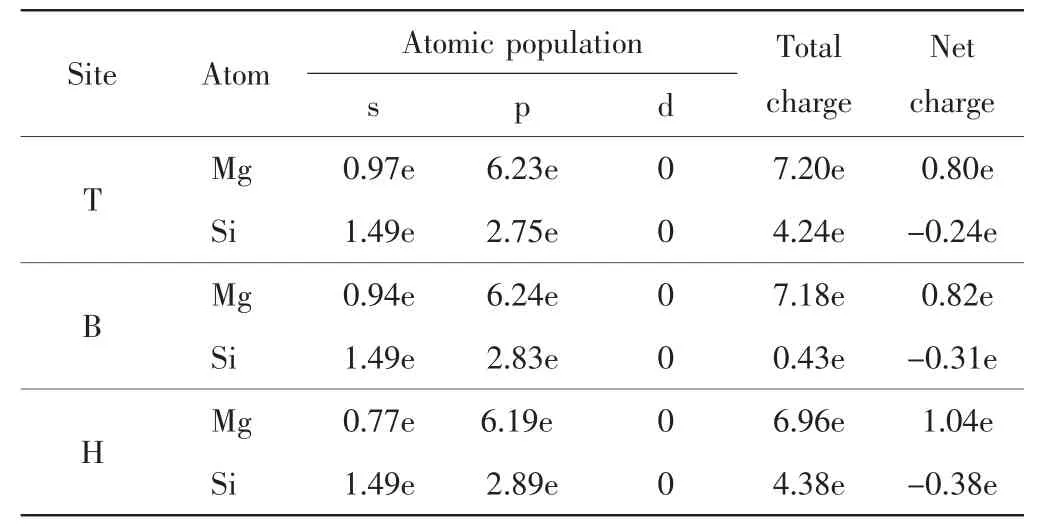
表3 不同吸附位置Mg原子與最近Si原子的電荷布居數Tab.3 Net M ulliken charges of Mg atom on the nearest Si at different adsorption sites

Mg原子失去電子表現為金屬性，Si原子獲得電子表現為非金屬性.不同吸附位置Mg和Si原子間的得失電子情況不同.頂位、橋位和穴位Mg原子失去電子數分別為0.80、0.82和1.04，說明Mg原子在相對穩定的穴位處失去電子的能力更強，失去的電子數最多[14].由此可知，與吸附在頂位和橋位相比，Mg原子吸附在Si（220）晶面的穴位時，Mg和Si原子間存在較強的離子鍵和共價鍵，Mg與Si之間的作用力更強，形成的吸附結構也更穩定.

2.4 Mg/Si（220）吸附體系的電子態密度

電子態密度圖反映了吸附原子與吸附晶面間電子態的分布和相互作用情況.本研究對Mg原子吸附于Si（220）表面穴位的情況進行分析，得到Mg原子在Si（220）表面穴位吸附前后體系的分波態密度（PDOS）和總態密度（TDOS），結果如圖3所示.

圖3（a）和圖3（b）分別為Mg原子吸附前后的分波態密度（PDOS）.由圖3（a）可以看出，費米能級附近存在電子分布，表現出很強的金屬性.由圖3（b）可以看出，費米能級附近幾乎無電子分布，表現出半導體的性質[15].比較圖3（a）和圖3（b）可知，Mg原子吸附在Si（220）面后，Mg原子的2p電子從0 eV附近移動到-10 eV附近，能量有所降低，且Mg原子3s電子的峰值降低明顯.

圖3（c）和圖3（d）分別是吸附前后Si（220）面的分波態密度（PDOS）.對比圖3（c）和圖3（d）可知，在吸附后的-7.5~-5 eV能量區間內，Si原子的3p電子向右移動，能量比吸附前有所增加.在0~2.5 eV能量區間內，吸附后Si原子3p電子的峰值不但有所降低，且峰的數量減少1個.對于Si（220）面來說，吸附前后變化明顯的是Si原子的3p電子.

圖3（e）和圖3（f）分別為吸附前后體系的總態密度（TDOS）.對比圖3（e）和圖3（f）可知，吸附Mg原子前，Si（220）面的價帶在-12.5~0 eV能量區間，導帶在0~3 eV能量區間；吸附Mg原子后，Si（220）面的價帶有-45~-43 eV和-12.5~0 eV共2個能量區間，導帶在0~2.5 eV能量區間.對比圖3（c）和圖3（e）可知，價帶能量區間和導帶能量區間均主要由Si 3s和Si 3p電子貢獻，但最主要貢獻來自于3p電子，3s電子的貢獻相對較小[16].此外，吸附Mg原子前，-45~-43 eV能量區間內未出現峰值，吸附后卻出現了1個小尖峰，這表明Mg原子吸附在Si（220）面后，電荷間的相互作用導致了該尖峰的出現.

綜上所述，Mg原子吸附在Si（220）表面后，總態密度（TDOS）在較低能量區間-45~-43 eV內出現了一個較為明顯的峰值，這個峰由Mg原子與吸附面的Si原子相互作用產生[17]，因此，Mg原子和Si表面的相互作用主要源于Mg原子的3s、2p電子和Si原子的3s、3p電子.

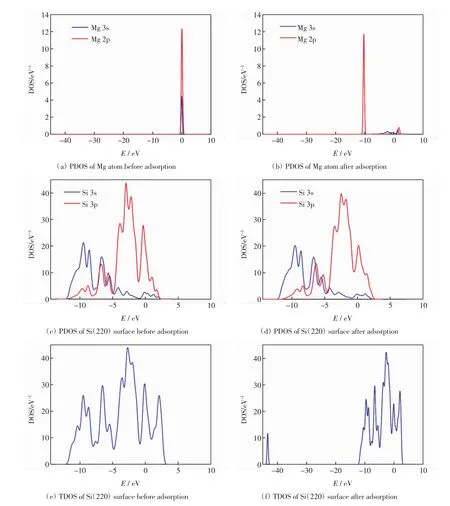
圖3 Mg原子和Si(220)表面穴位吸附前后的態密度(DOS)Fig.3 DOS of Mg atom and Si（220）surface before and after adsorption on hollow site

3 結論

本研究采用第一性原理方法對Mg原子在Si（220）晶面的表面吸附行為進行計算，研究結果表明：

（1）吸附的最穩定結構是Mg原子的初始位置在Si（220）表面的穴位.此時的吸附能為-3.53 eV，屬于穩定吸附.

（2）當Mg原子在Si（220）表面的吸附處于穴位時，吸附形變最大，且被吸附Mg原子與吸附面的距離最近.這說明此位點比頂位和橋位具有更強的吸附力，吸附結構更穩定.

（3）Mg原子吸附在Si（220）表面后功函數均變小，說明Si（220）表面吸附Mg原子后電子發生轉移.

（4）Mg原子吸附在Si（220）表面的穴位時，Mg與Si原子間存在較強的離子鍵和共價鍵，增強了Mg與Si間的作用力，形成了更穩定的吸附結構.

（5）Mg原子吸附在Si（220）表面后，總態密度（TDOS）在較低能量區間內出現1個較為明顯的峰值.該峰由Mg原子的3s、2p電子和Si原子的3s、3p電子相互作用產生.