高速主軸不平衡振動行為分析與抑制策略

章云,孫虎,胡振邦,梅雪松

(1.西安電子科技大學機電工程學院,710071,西安;2.中航工業陜西航空電氣有限責任公司,713107,西安;3.西安交通大學機械制造系統工程國家重點實驗室,710049,西安)

現代高品質加工表現出高速、高精度等特點,高速主軸是高品質加工的核心部件,其動態性能直接影響零件的加工的效率及精度[1-2]。主軸運行過程中,由于安裝偏心、磨損等原因導致主軸慣性中心線不在主軸回轉線上,即存在不平衡現象。不平衡力與轉速的平方成正比,在高轉速情況下,即使不平衡量微小,也會產生較大的離心力,引起主軸的不平衡振動[3]。高速加工技術中,主軸振動對加工的質量和效率影響極大,甚至導致某些功能部件的破壞。

盡管國內外學者在不平衡振動抑制問題上投入了大量精力[4-7],但工業現場時有平衡不徹底或盲目平衡的現象發生:對主軸進行低速動平衡后,即使主軸最高轉速低于一階臨界,但其低速動平衡效果在高速下仍無法繼續保持;以主軸不同位置測點的振動信號為依據進行動平衡配重計算,其結果往往不一致,甚至相互矛盾。這類現象在基于測試數據進行動平衡的方法中尤為明顯,許多學者在動平衡實施過程中增加了主軸動力學特性信息,并在動平衡的實施過程及效果上取得了一定的進展[8-11]。

不平衡狀態無法直接測量,動平衡方法的分析對象是不平衡所激發的振動響應,而不是不平衡本身。高速運轉的不平衡主軸系統內部呈現非線性特征[12],這直接導致了高速下不平衡狀態的逐漸演變。與此同時,各類耦合故障、復雜工況的干擾也會進一步加劇不平衡主軸的振動形態的復雜度。

因此,本文基于有限元思路,建立了主軸系統動力學模型,通過仿真與實驗結合的方式對模型的有效性進行了驗證,進而分析了不平衡激勵下主軸轉子空間振動行為,提出了基于模型的不平衡振動抑制策略,并給出了現場驗證效果。

1 高速主軸系統動力學模型構建

典型的主軸有限元模型由離散質量圓盤、具有分布質量的軸段以及彈性軸承座等單元組成[13],各單元間彼此在節點處聯接。主軸轉子系統結構如圖1所示,對于具有N個節點、其間用N-1個軸段連接而成的主軸系統,每個單元的位移向量為δ={δxn,δyn,δzn,θyn,θzn}T∈RN×1,n=1,2,…,N。

圖1 主軸轉子系統結構

對于采用角接觸滾動球軸承支承的高速主軸,基于Jones軸承模型[14],構建由變形協調方程和力平衡方程得到的軸承滾動體非線性方程

(1)

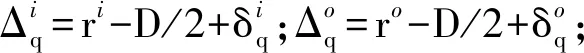
(2)

式中:τ={τ1,τ2,τ3,τ4}T為迭代誤差項;λ=?ηq/?τ,λ∈R4×4。

基于迭代所得參數可以求解軸承的接觸角與接觸力,進而可得到所有滾珠與軸承內、外圈之間接觸力的疊加合力Fb={Fx,Fy,Fz,My,Mz},該合力為位移向量δ的函數,將合力對位移求偏導即可得到軸承的剛度矩陣Kb。

對于主軸轉子上的平衡環、編碼盤以及電機繞組等質量相對集中單元,其可視為由位于圓盤中心的一個節點構成的五自由度剛性圓盤單元,單元運動方程可表示為

(3)

式中:Ω為主軸轉速;Md∈R5N×5N為圓盤單元的質量單元;Gd∈R5N×5N為考慮陀螺效應的反對稱矩陣;Fd∈R5N×1為圓盤偏心導致的不平衡離心力。

對于主軸轉子主體部分,可視為梁單元,其有限元運動方程可寫為

(4)

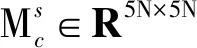
對主軸各單元矩陣進行集成,可得到主軸系統動力學有限元方程

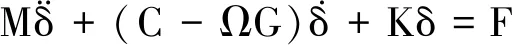
(5)

2 高速主軸系統動態特性測試

為了對主軸動力學特性進行分析,建立有限元模型,主軸轉子總長為560 mm,模型中將主軸劃分為58個梁單元,即共計59個單元節點,高速主軸有限元模型節點分布如圖2所示。兩個配重盤以及旋轉編碼器作為圓盤單元,其節點位置分別6、24和54,兩個滾動軸承單元所在節點號為18、45。主軸轉子與滾動軸承內外圈的材料密度為7.8×103kg/m3,彈性模量為208 GPa,泊松比為0.3,軸承內圈內徑與外圈外徑分別為25、52 mm,寬度為15 mm。軸承內共均勻分布32個滾動體,其泊松比為0.26,彈性模量為315 GPa,滾動體直徑為7 mm,接觸角為25°。

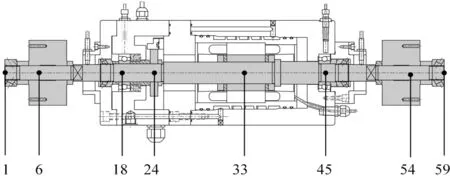
圖2 高速主軸有限元模型節點分布

為驗證式(5)所構建主軸動力學模型的有效性,通過Ansys商業軟件進行主軸建模,其中主軸主體和軸承分別采用SOLID187和COMBI214單元構建,兩者之間的連接基于接觸單元TARGE170和CONTA174建立。將Ansys分析結果與基于式(5)的Matlab計算結果進行分析,彎曲振動前3階振型的Matlab、Ansys分析結果如圖3、圖4所示,可知兩者所求解振型的整體形貌變化規律相同。Matlab和Ansys仿真分析得到的主軸端部徑向位移諧響應曲線對比圖如圖5所示,Matlab和Ansys仿真分析得到的前3階諧振頻率的對比見表1。

(a)1階 (b)2階 (c)3階圖4 彎曲振動振型Ansys分析結果

(a)1階 (b)2階 (c)3階圖3 彎曲振動振型Matlab分析結果

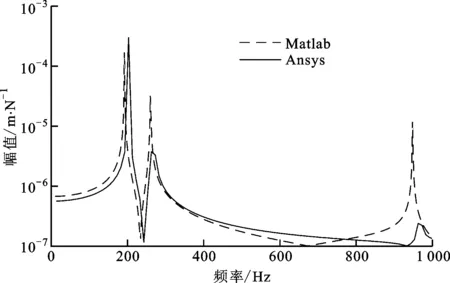
圖5 Matlab和Ansys仿真分析得到的諧響應曲線對比圖

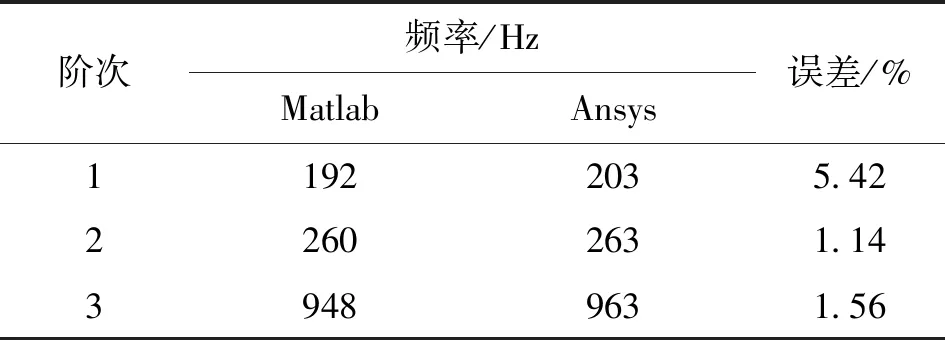
階次頻率/HzMatlabAnsys誤差/%11922035.4222602631.1439489631.56

由圖5、表1可知,Matlab和Ansys的頻響曲線契合度很高,頻響峰值處對應的固有頻率誤差分別為5.42%、1.14%、1.56%,由Matlab和Ansys分別計算的主軸動態特性基本相同,這反映了式(5)所建動力學模型的有效性。

高速主軸系統動態特性實驗測試平臺如圖6所示,平臺采用壓電式加速度傳感器ULT2001及沖擊力錘LC-01A獲取頻率響應信息,采用電渦流位移傳感器WD502A及光電傳感器E32-ZC31N獲取主軸不平衡振動及相位信息,數據的實時記錄與顯示通過INV3018CT數據采集儀來實現。

圖6 高速主軸實驗驗證平臺

在主軸末端施加激勵,結合加速度傳感器信號,可獲得實驗頻率響應曲線,如圖7所示。由圖7可知:基于實驗獲取的主軸頻率響應曲線的峰值分別為192.3、271.9、1 008 Hz,諧振頻率的誤差分別為0.16%、4.38%、5.95%,這表明仿真分析與實驗結果匹配程度較高,即該模型能可靠地描述主軸的動態特性;受激勵施加及響應測量位置、主軸轉子裝配狀態、主軸系統內部組件等因素的影響,實驗頻率響應曲線會略有差異。在實際高速運轉中,主軸諧振頻率與陀螺效應、軸承特性等諸多因素相關,這會導致仿真與實測結果之間略有出入。

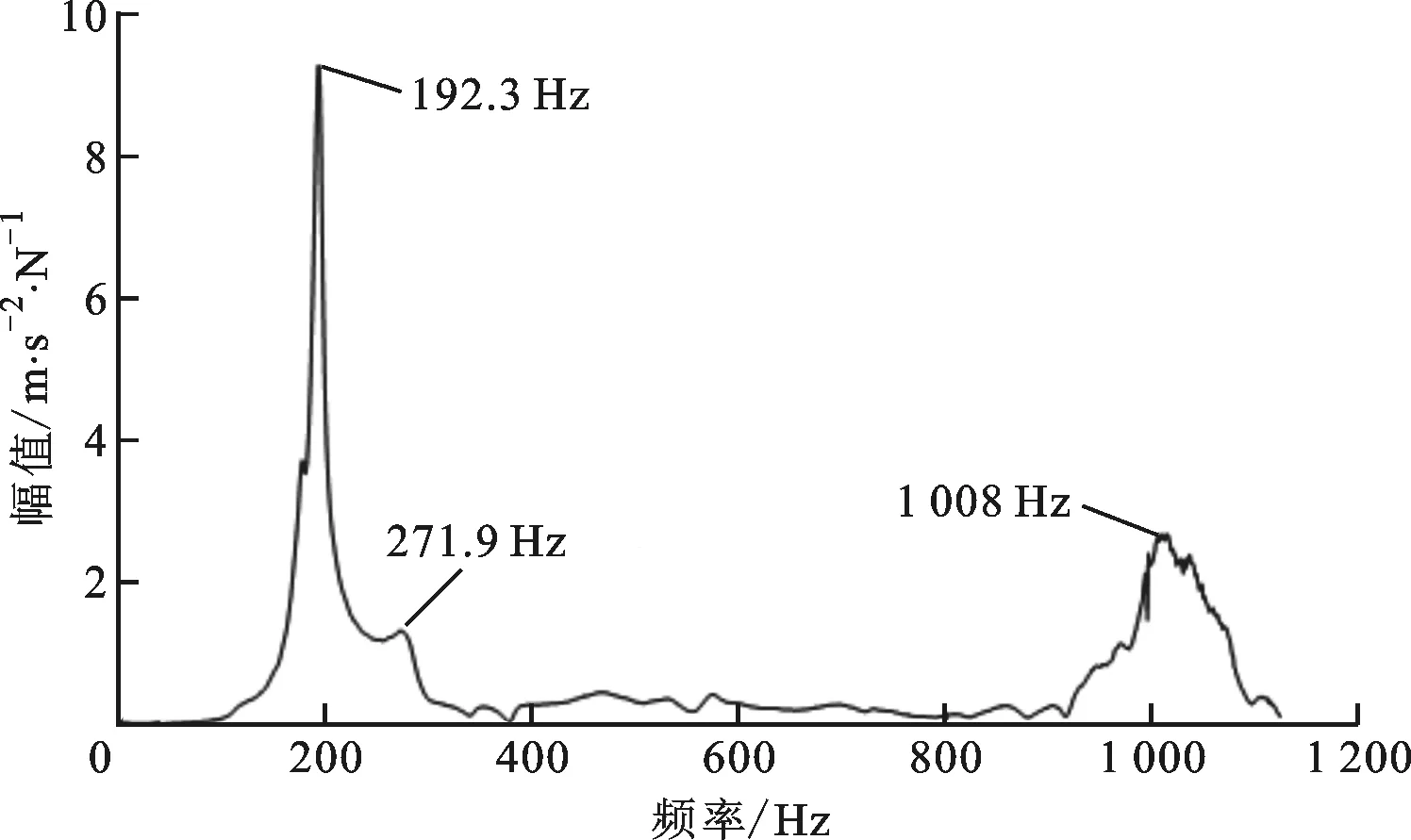
圖7 高速主軸末端實驗頻率響應曲線

3 主軸空間振動行為分析

主軸受到不平衡激勵時,將產生受迫振動,若偏心量為ε,初始相位φ0為0°,則主軸系統受到的不平衡激勵可表示為

F(t)={F1(t),F2(t),…,F59(t)}T

(6)

式中Fi(t)={0,Fyi,Fzi,0,0}T(i=1,2,…,59)為每個節點上的不平衡激勵,Fyi+iFzi=mεiεΩ2ei(Ω t+φ0)。

若主軸左右端節點6、54處具有不平衡質量mε6=2g、mε54=1g,ε為37mm,主軸轉速為6 000r/min,不平衡激勵如圖8所示。在激勵作用下主軸不同位置的響應不同,研究不同位置響應可以確定主軸在該激勵作用下的振動傳遞規律。

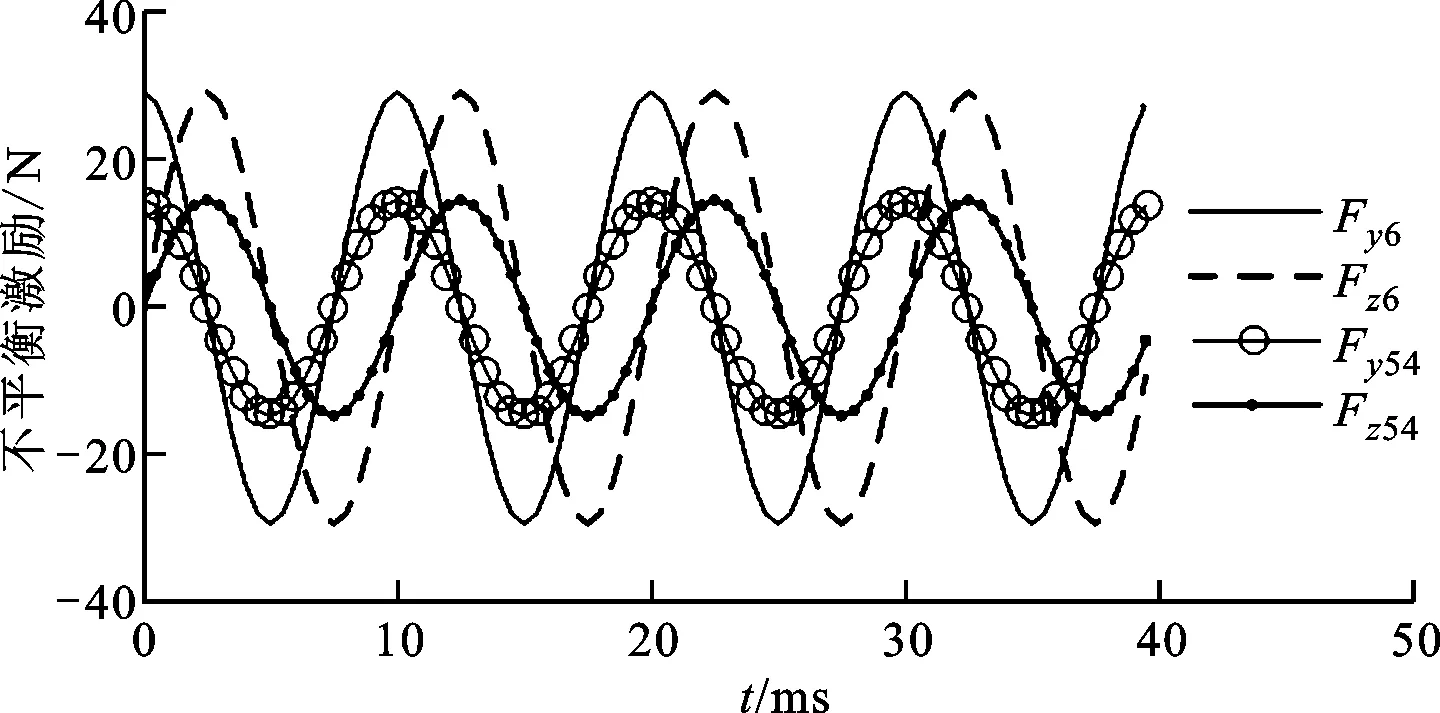
圖8 不平衡激勵

不平衡激勵確定后,結合有限元模型可求解不平衡響應,此處選取主軸左右端、軸承、編碼器、電機繞組以及配重盤處等關鍵節點進行分析,根據轉軸y與z向運動的相似性、對稱性,以y向振動為例,yi表示y向第i(i=1,2,…,59)個節點,不平衡激勵下徑向和扭轉響應過程如圖9、圖10所示。

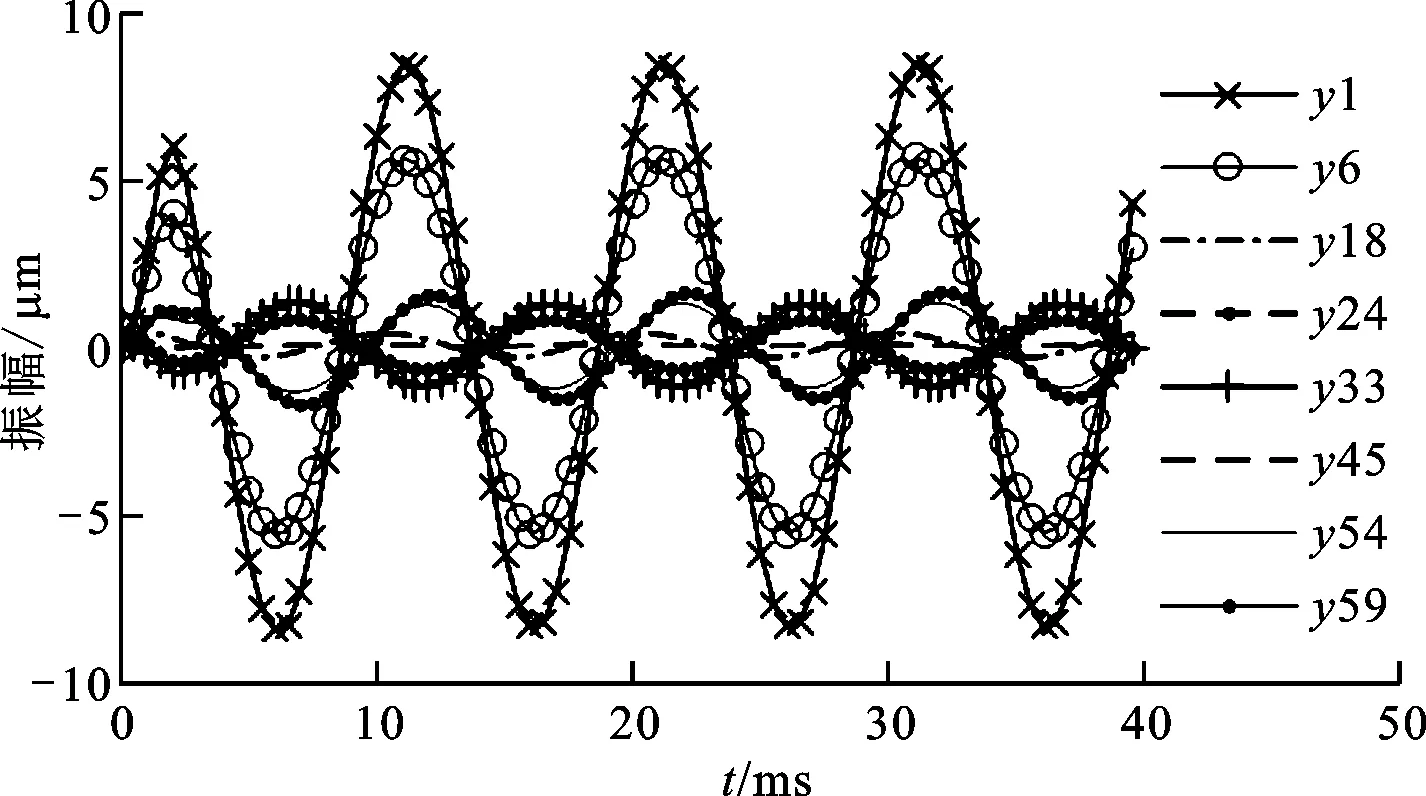
圖9 不平衡激勵下徑向響應過程

由圖9可知:在不平衡激勵下,主軸振動迅速進入穩態,且不平衡振動與激勵同頻;主軸左右端節點1、6、54、59振動較為明顯,且由于左端不平衡激勵較大,故左端節點1、6振動明顯大于右端節點54、59;主軸軸承節點18、45處振動受軸承外圈約束,振動幅值非常小。主軸軸承外側節點1、6、54、59振動與兩側軸承之間的中央節點24、33振動相位近乎相反,其原因在于圖3a中第1階振型在兩軸承中間位置,與軸承外側是反向的,而當主軸運行在6 000r/min即第1階臨界轉速以下時,其振動行為主要受第1階振型影響,故符合主軸第1階振型形貌分布特性。

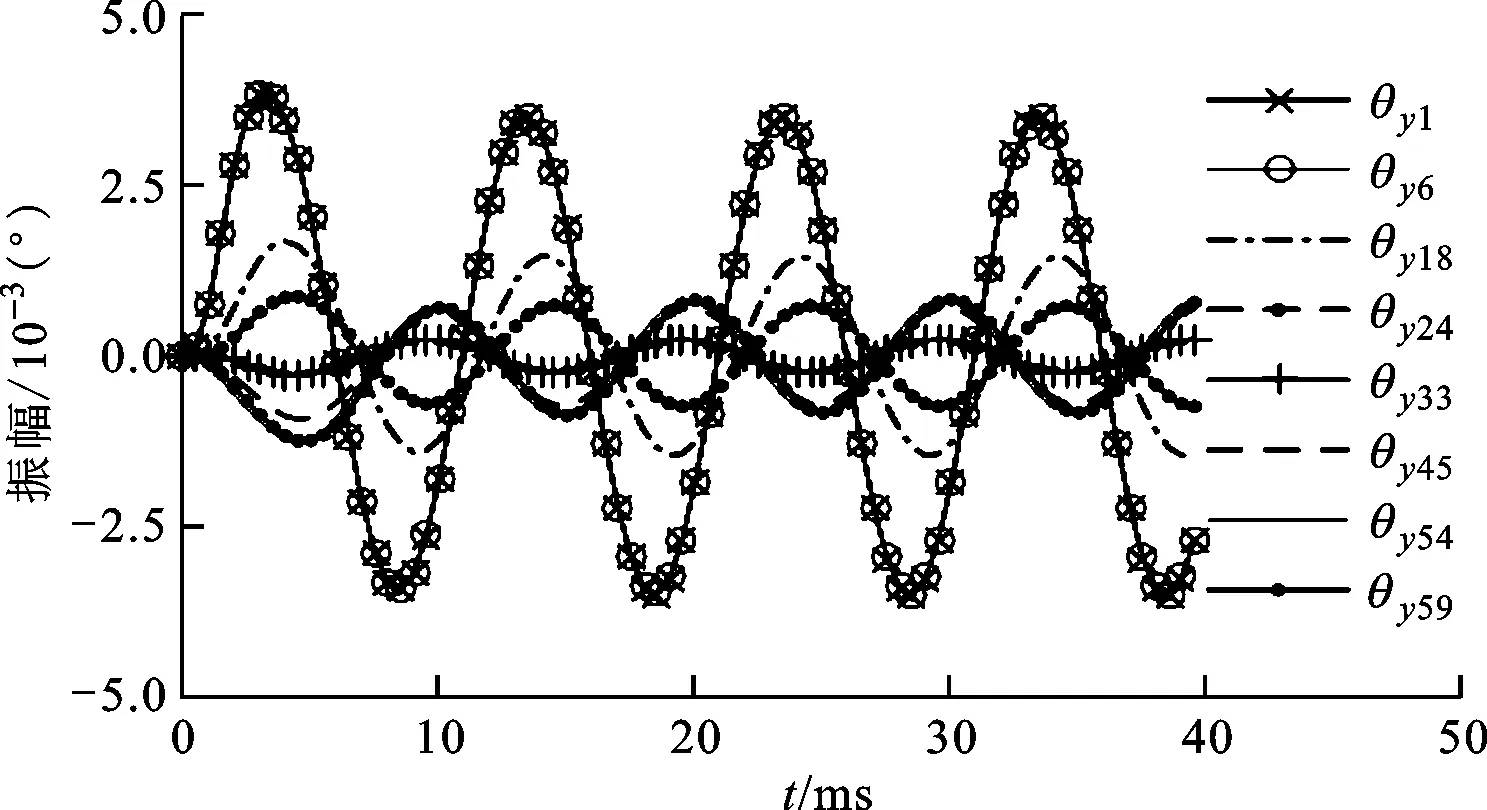
圖10 不平衡激勵下扭轉響應過程

由圖10可知:主軸左端節點1、6扭轉位移明顯大于右端節點54、59,符合不平衡激勵左端大于右端的加載特征;軸承外端同側延伸節點1與6、54與59的扭轉位移基本一致,符合主軸軸承外側延伸懸臂端扭轉變形物理特征;軸承節點18、45處扭轉位移較為明顯,說明在軸承處雖然其振動幅值較小,但在該處轉子偏轉較為明顯,這符號軸承的約束特征和圖3a第1階振型在主軸軸承處斜率較大的特征。中間節點33扭轉位移最小,兩側節點扭轉位移較大,主軸轉子整體扭轉響應符合第1階振型曲線斜率特征。

為分析主軸轉子在不同不平衡激勵下的響應特性,mε54保持不變,mε6從0遞增至3g,不平衡激勵變化下各節點的徑向響應和扭轉響應如圖11、圖12所示。由圖11可知,隨著不平衡質量的增加,主軸徑向位移與扭轉位移均呈上升趨勢,145、423mm處為軸承位置,故受不平衡質量的影響不明顯,幅值較小。圖12表現出同樣的整體變化趨勢,但因其為扭轉位移,故其最小值不再在軸承處,而表現在軸承中間275mm處,該處在圖11中為極值點位置,徑向位移曲線斜率最小。

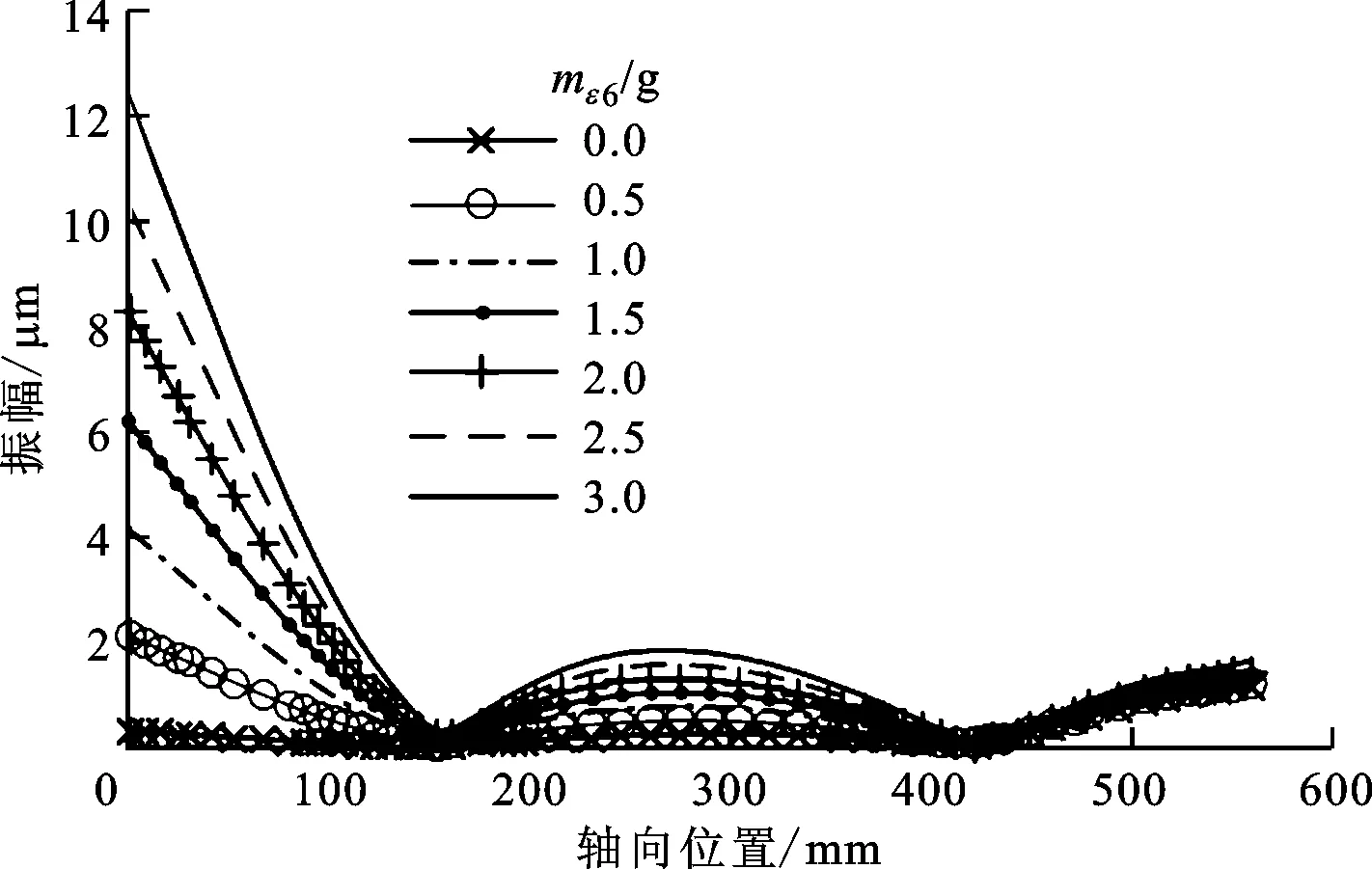
圖11 不平衡激勵變化下各節點的徑向響應

圖12 不平衡激勵變化下各節點的扭轉響應

4 基于模型的不平衡振動抑制策略

不平衡激勵會導致主軸轉子空間多自由度振動,為實現空間振動的抑制,可將轉子不同自由度振動按不同權重組合,構建平衡目標,但在現場平衡過程中,通常僅采用徑向振動作為平衡目標,其原因一方面在于徑向振動與不平衡激勵的方向一致,相對于其他自由度振動,兩者相關性更明顯,即空間振動的平衡目標中,徑向振動的權重遠高于其他自由度振動;另一方面由于主軸系統的結構限制,通常僅能獲取主軸徑向振動。實際上,以徑向振動為平衡目標,經動平衡操作后,各自由度不平衡振動都能得到有效降低[15]。

結合主軸動力學模型,可將不平衡力等效到模型節點之上,通過力學分析得出不同轉速下徑向振動與不平衡矢量之間的關聯關系,實現不平衡量的求解。式(5)中振動響應特解為δ=AeiΩt,其中A={a1eiφ1,a2eiφ2,…,aNeiφN}T∈CN,式(5)可變形為

Ω-2[-Ω2INiΩIN-iΩ2ININ][MCGK]TA=U

(7)

式中:U={u1,u1,…,uN}T∈CN為分布在節點上的不平衡矢量;IN∈RN×N為單位對角矩陣。

若不平衡節點數為N,振動測量節點數為J,為求解不平衡矢量U,則需要測振轉速的數量H為N/J,式(7)可擴展、變形為

[u1u2…uN]T

(8)

為驗證動力學模型及不平衡識別策略的有效性,需開展動平衡驗證。根據第1階振型分布,不平衡振動在主軸兩端體現的較為明顯,實驗平臺上對主軸轉子兩端都進行監測,每個測量面上的兩個電渦流位移傳感器呈相互垂直方位安裝,光電傳感器則用于獲取振動相位。由于主軸轉子在裝配前已進行過離線動平衡,運轉時不平衡激勵主要源于兩側質量盤,根據式(8),僅需一個轉速即可完成不平衡激勵識別,實驗轉速設為9 000 r/min。主軸運行穩定后,提取振動工頻值,結合主軸動力學模型數據,求解得到兩側質量盤上的不平衡量分別為7.99、8.30 g·mm,所在相位分別為-179.18°、-151.88°,根據識別結果實現動平衡校正后,主軸振動抑制情況如圖13所示,其中外圈三維全息譜圖為原始振動,內圈譜圖為平衡后的殘余振動。主軸動平衡前后振動結果如表2所示。

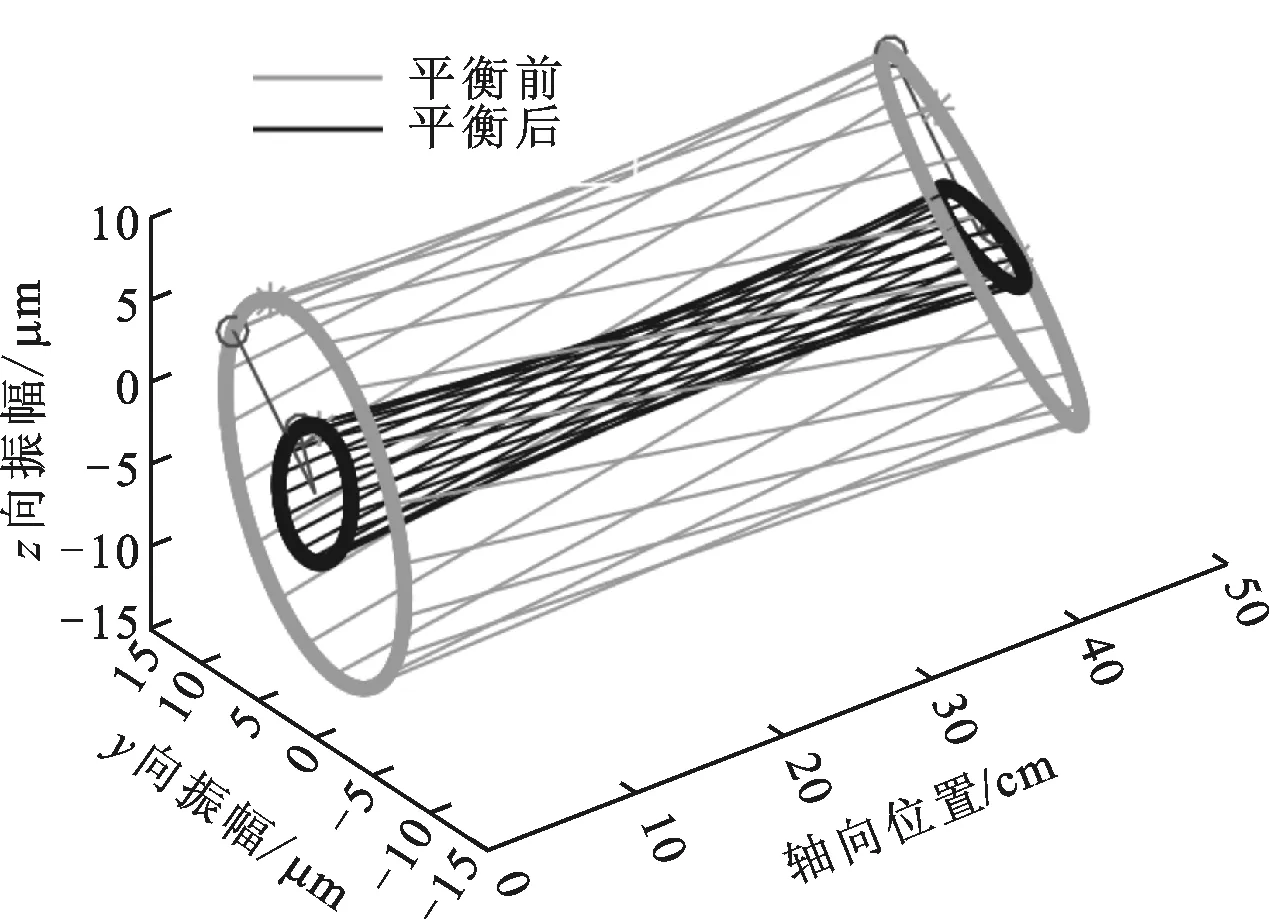
圖13 主軸動平衡前后三維全息圖譜對比

測振位置振動幅值/μm平衡前平衡后降幅左截面y方向7.872.7465.2%z方向10.463.9162.6%右截面y方向8.822.8467.9%z方向7.721.7577.4%

由圖13、表2可知,主軸動平衡后,不平衡振動抑制效果較為明顯,這反映了本文主軸動力學模型及不平衡振動抑制策略的有效性。圖13中動平衡前后振動初相矢的方位發生了一些變化,這主要是由于平衡后振動信號的信噪比降低,提取工頻振動時受噪聲干擾影響,以及轉子輕微各向異性所致。表2中殘余振動沒有降至零,主要是由于動平衡效果受到轉軸彎曲等呈現工頻特征的非失衡故障、配重質量加載精度以及模型構建偏差等的影響。

5 結 論

本文構建了高速主軸動力學模型,并通過實驗驗證了模型的有效性,進而分析了高速主軸在不平衡振動行為及抑制策略,得到如下主要結論。

(1)不平衡響應曲線形貌受不平衡激勵和振型共同影響,整體符合振型特征;在局部區域,響應節點距離不平衡激勵節點越近,位移幅值越大,且按照振型特征變化。

(2)不平衡激勵越強,振動幅值越大,兩者呈現單調遞增關系;受阻尼影響,即使激勵與響應為同一節點,兩者也存在略微的相位延遲;受結構的限制,在軸承等節點的不平衡響應會受到約束。

(3)基于模型的不平衡振動抑制方法,本文構建了不平衡振動與不平衡矢量之間的傳遞關系,無需添加試重,僅需在低于臨界轉速下采集振動數據,就可實現振動的有效抑制。