燃氣輪機拉桿轉子非線性動力學特性研究

達琦,袁奇,李浦

(1.西安交通大學能源與動力工程學院,710049,西安;2.西安交通大學陜西省葉輪機械及動力裝備工程實驗室,710049,西安)

拉桿轉子常用于重型燃氣輪機和航空發動機,通過在中心或周向拉桿螺栓上施加預緊力來保證多級輪盤之間的相對靜止并使輪盤段具有一定剛度。然而,即使受到較小的彎曲外載荷,轉子輪盤接觸面仍會部分區域脫開[1],導致接觸面積減小進而造成轉子整體剛度下降。文獻[2]對某航空發動機的鼓筒式轉子接觸段剛度進行研究,結果表明輪盤之間的相對轉角隨彎矩線性增加呈現出非線性的變化規律。在建立具有螺栓連接結構的航空發動機轉子力學模型時,常采用角剛度分段線性模型來近似連接部位的剛度變化規律[3]。與連續轉子相比,角剛度分段線性模型的動力學響應與線性模型的動力學響應存在較大差異。為了解釋組合轉子升速和降速中存在的振幅突跳現象,有學者綜合考慮輪盤接觸面和拉桿剛度的共同作用,建立具有三次方剛度的轉子模型[4-5]。拉桿轉子的特殊結構使得連接段剛度具有非線性的變化規律,且組合式轉子多個輪盤之間的接觸模式可能不同,因而其動力學響應十分復雜[6];在特定條件下,幅頻響應中出現的線性系統所不具有的雙穩態現象使得轉子故障頻發,造成了巨大的經濟損失。對于非線性轉子系統出現的振幅突跳現象,國內外學者從不同角度進行研究[4,7-10],將其視為轉子系統的一種故障,并盡量設法避免。目前國內對于拉桿轉子非線性振動特性研究較少,以往的文獻均采用剛度硬化模型,即整體剛度隨轉速增加而增加,對于幅頻響應中出現的振幅突跳現象無一致結論,且現有分析模型缺乏依據。

針對以上問題,本文首先利用三維非線性有限元方法計算得到拉桿與接觸面等效剛度隨輪盤橫向間距的變化規律;然后分別采用雙線性模型和三次方模型擬合非線性剛度曲線,建立兩種拉桿轉子力學模型;最后通過數值仿真分析,對兩組模型幅頻響應中出現的非線性振動現象進行了對比研究,進而分析不同系統參數對轉子振動特性的影響。

1 拉桿轉子橫向剛度分析

圖1為周向拉桿組合式轉子模型,該模型由軸頭、輪轂、輪盤、拉桿和接觸面組成,l3、l4分別為輪轂和輪盤的軸向長度,2l1表示輪轂和輪盤總長度,l2為軸頭長,模型總長為2l。將輪盤接觸面和拉桿的剛度一并考慮,Ks、Kh、Kds、Kr分別表示軸頭、輪轂、輪盤和拉桿的抗彎剛度。

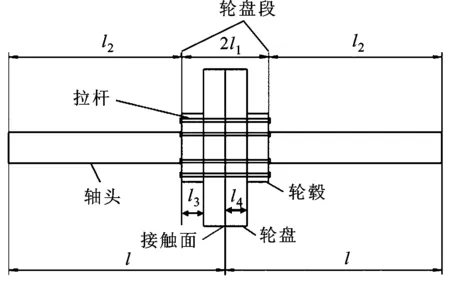
(a)拉桿轉子示意圖

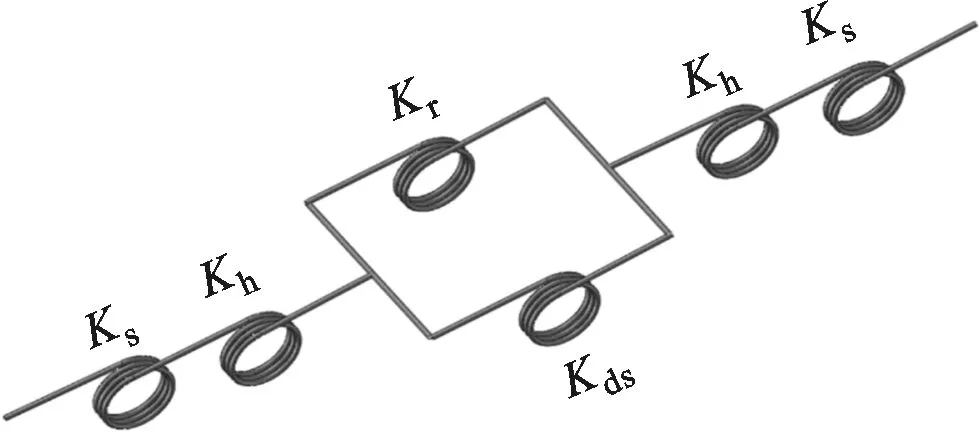
(b)轉子彎曲剛度模型圖1 周向拉桿組合式轉子

轉子輪盤段的剛度可表示為

(1)

利用彎矩-轉角關系和有限元軟件計算輪盤段的抗彎剛度

(2)

Kfij表示在j方向上引起轉子在i方向上產生單位轉角所施加的彎矩。

為簡化分析,認為轉子各向同性,并不計交叉方向上的剛度,彎曲剛度可以表示為

(3)

(4)

式中δij為克羅內克函數。利用式(3)可以在三維有限元軟件ANSYS中求出輪盤段的抗彎剛度Kc,然后將Kc代入式(1)計算得到Kr。

用力矩-面積法求輪盤段的橫向剛度

(5)

利用力矩面積法分別得到輪轂和輪盤的橫向剛度Khl、Kdsl,然后根據Kcl、Khl、Kdsl和Krl之間的關系,即可得到拉桿和接觸面的等效橫向剛度

(6)

由于輪盤相對轉角很小,認為sinφ≈φ,因此兩輪盤間距X近似表示為φl,其中l為接觸面到軸頭的距離,橫向位移與轉角關系示意圖如圖2所示。

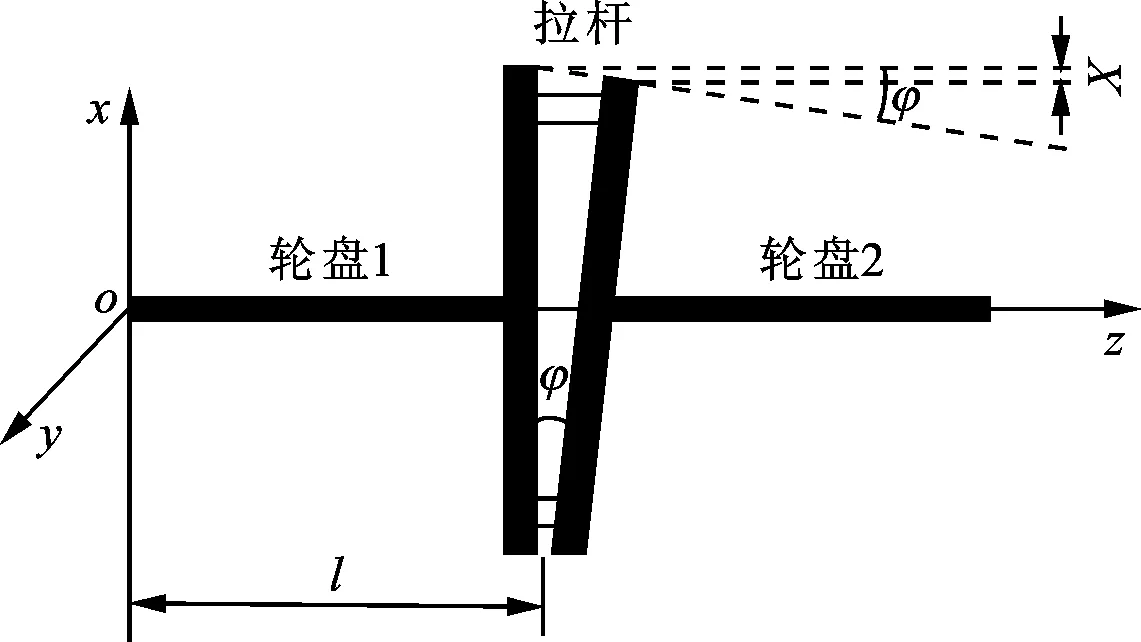
圖2 轉子輪盤橫向位移與轉角關系示意圖

等效剛度對應的橫向回復力可表示為

Frl=KrlX

(7)

利用有限元軟件ANSYS建立上述三維有限元模型,如圖3所示,模型的參數取值如表1所示。

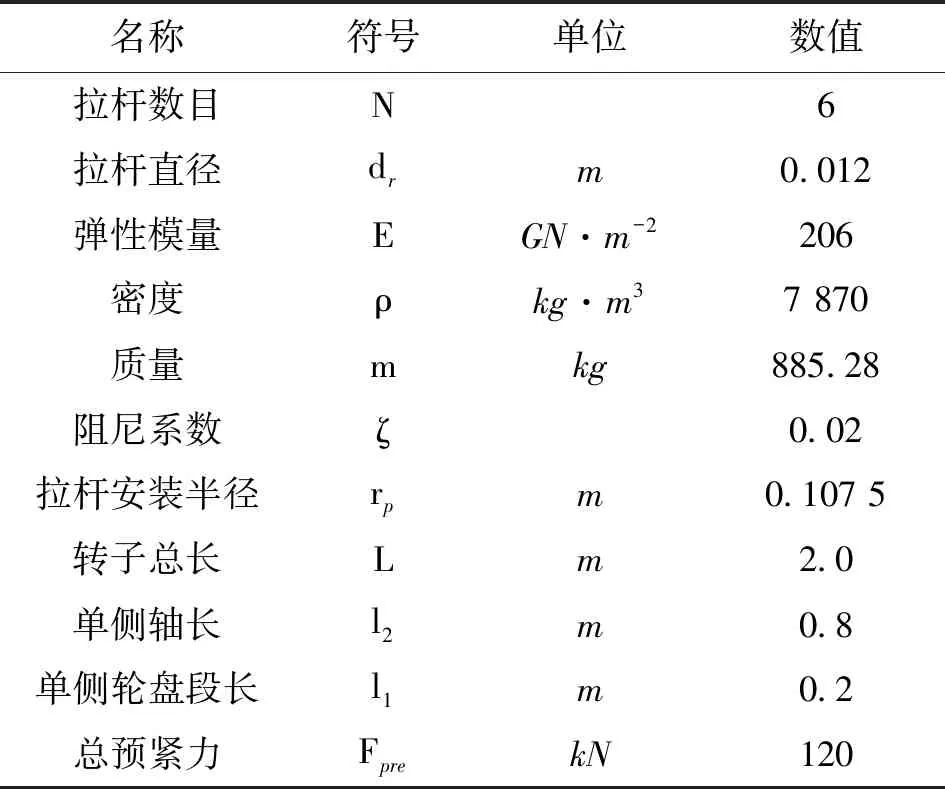
表1 模型轉子物理參數

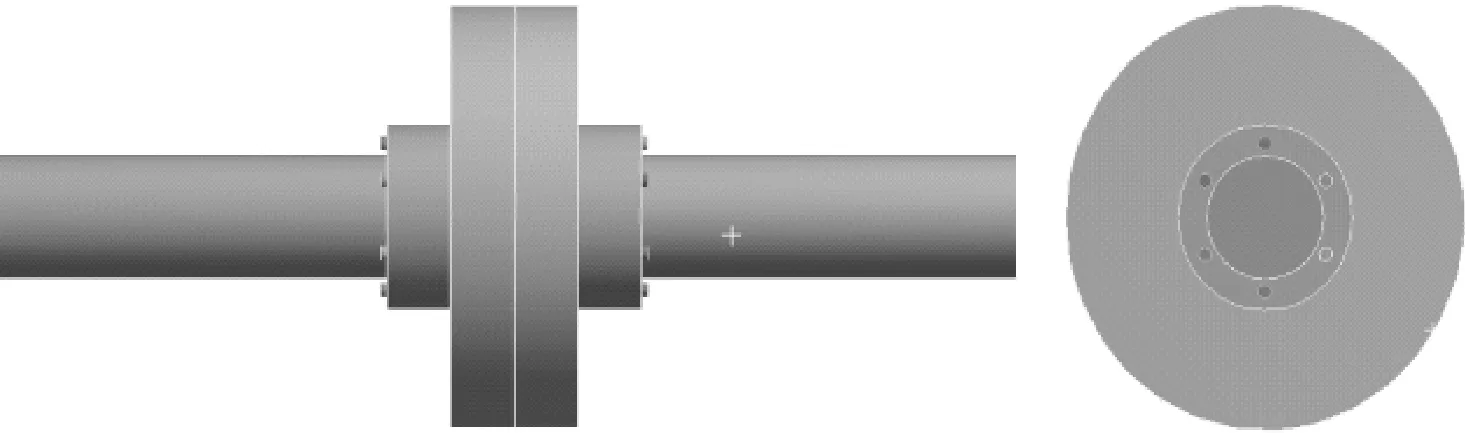
圖3 拉桿轉子三維有限元模型

參考文獻[11]的方法,利用式(3)計算得到輪盤相對轉角φ隨彎矩M變化關系,如圖4所示,并根據式(5)(6)計算得到等效橫向剛度值|Krl|隨兩輪盤間距X的變化曲線,如圖5所示。

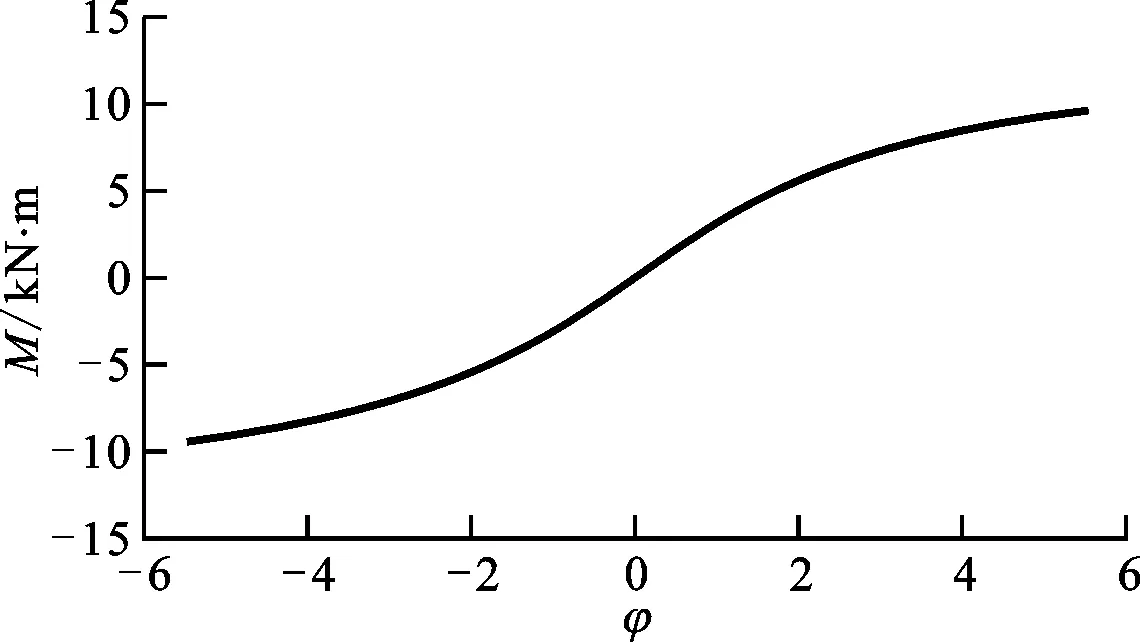
圖4 輪盤間相對轉角隨彎矩變化關系

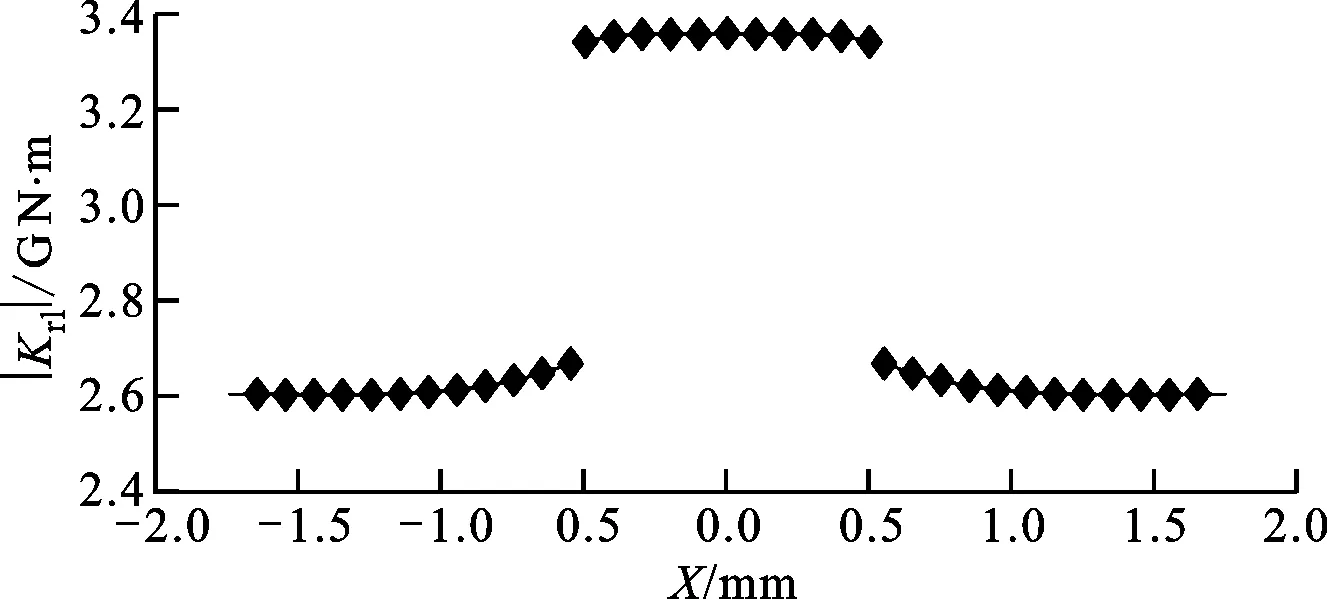
圖5 等效橫向剛度隨輪盤間距變化曲線

2 轉子動力學方程建模

將兩輪盤分別簡化為質量為m1、m2的剛性圓盤,兩盤質量偏心量取相同值且均用e表示,偏心量矢量夾角為θ。將拉桿和接觸面等效為不計質量的抗彎彈簧,回復力用F(q)表示,其中q為輪盤位移矢量。輪盤段兩端分別與不計質量的彈性軸相連,兩盤橫向剛度分別為k1、k2。左、右端軸和抗彎彈簧的阻尼系數分別表示為c1、c2、c3。轉子系統模型如圖6所示。

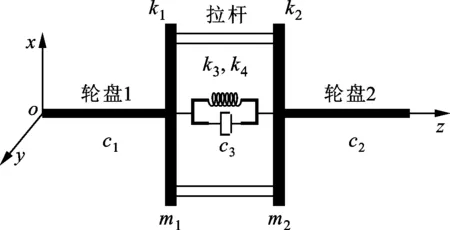
圖6 轉子系統模型示意圖

模型中單個輪盤的位移矢量表示為

qi=[xiyi]T

(8)

式中x、y為單個輪盤的自由度。

根據達朗貝爾原理建立系統運動方程

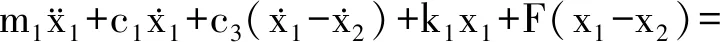
(9)

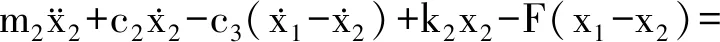
(10)

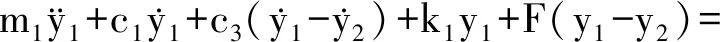
(11)

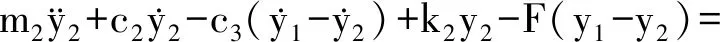
(12)

式中:Ω為轉子角速度;F(x1-x2)為非線性回復力。記X=[x1x2y1y2]T,式(9)～(12)的矩陣形式為

MX″+CX′+KX=f(t,X)

(13)

式中

3 三次方非線性剛度模型

由三維有限元計算結果如圖4所示,可知隨著接觸段載荷的增加,拉桿和接觸面等效橫向剛度呈非線性變化,其變化趨勢可以用三次多項式函數擬合,將回復力表示為

F(x)=k3x-k4x3

(14)

式中:k3為接觸段的線性剛度;k4為輪盤接觸面積減小造成兩輪盤橫向剛度削弱后的剛度。

3.1 模型動力學方程

動力學方程在x和y方向無耦合,根據控制方程的對稱性,只研究x方向的橫向振動。

令τ=Ωt,x3=x1-x2,k1=β2k2=β3k3=β4k4,將式(9)～(12)改寫為無量綱化形式

(15)

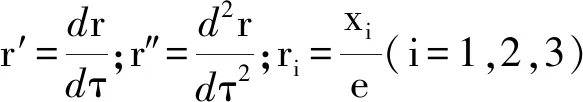
利用諧波平衡法近似求解式(13),動態響應形式解為

(16)

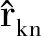
(17)

利用迭代算法求解式(17),可得方程組的近似解。

3.2 非線性代數方程組優化求解算法

3.2.1Broyden迭代算法Broyden算法具有超線性收斂速度,在一定條件下收斂速度快[12-13]。迭代過程可表示為

r(k+1)=r(k)-Ak-1f(r(k))

(18)

Aksk=yk

(19)

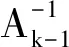
(20)

當殘差小于誤差限時求解收斂。

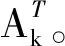
(21)

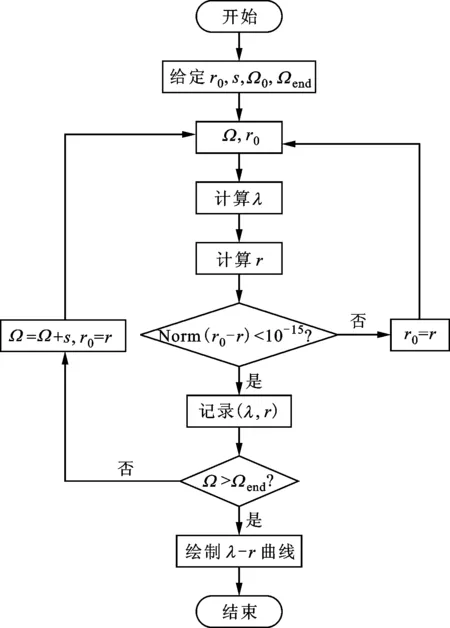
圖7 模型轉子幅頻曲線計算流程圖

3.3 計算結果與分析

計算時使用系統參數如表2所示。根據計算結果繪制拉桿轉子在升速和降速過程中的無量綱幅頻響應曲線,進而改變系統參數,分析不同系統參數對響應曲線的影響。

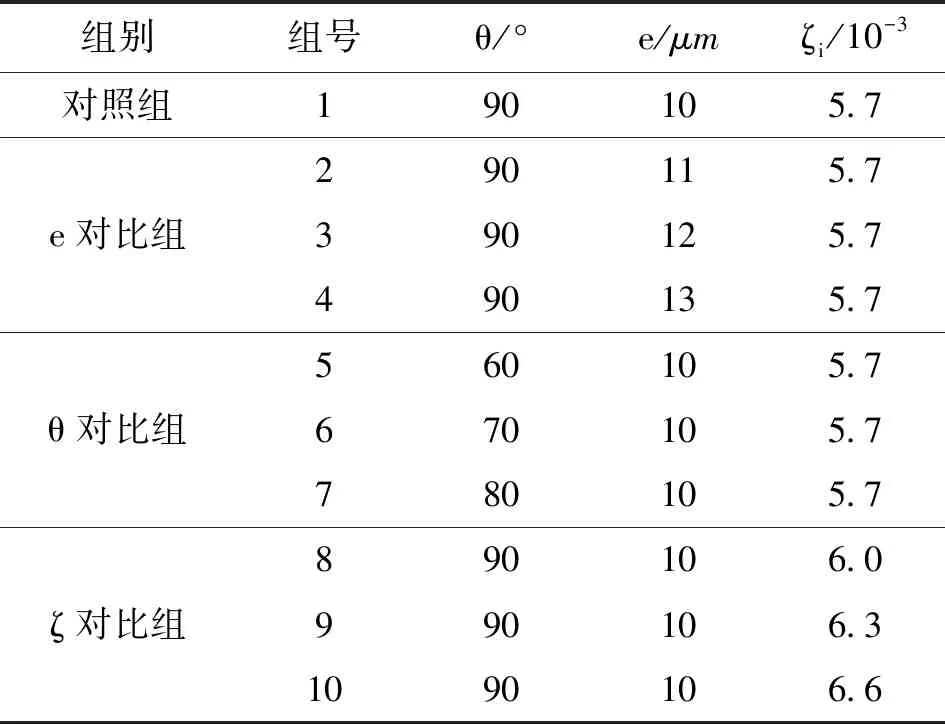
表2 拉桿轉子非線性系統參數取值

3.3.1 轉子升速和降速曲線 取表2中第1組參數,其余參數α=0.75,β2=1,β3=1,β4=5×105m-2,繪制輪盤質心x方向的相對幅值r隨轉子相對轉速λ變化曲線,如圖8所示,圖中rij表示第i個轉盤的j階諧波響應。由圖8可知:無量綱幅頻曲線具有一階、三階諧波,二階諧波幅值過小;兩輪盤無量綱幅頻響應曲線隨無量綱轉速變化趨勢相同,但幅值不同。

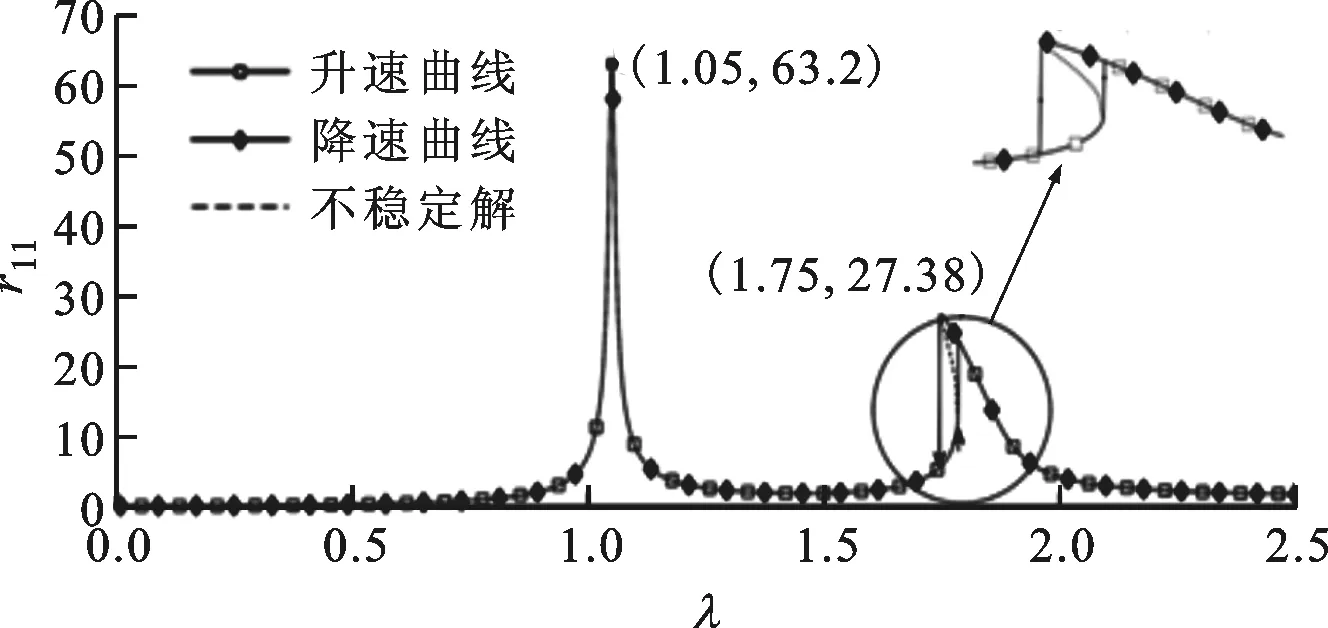
(a)輪盤1升速和降速一階諧波曲線

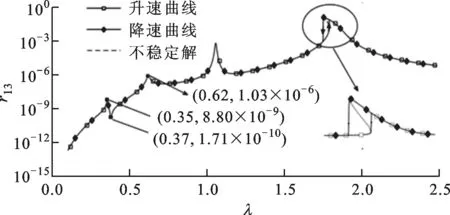
(b)輪盤1升速和降速三階諧波曲線

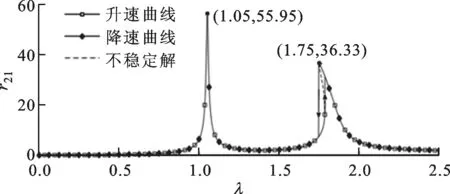
(c)輪盤2升速和降速一階諧波曲線

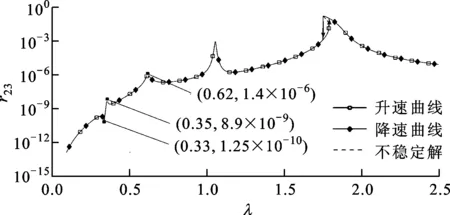
(d)輪盤2升速和降速三階諧波曲線圖8 拉桿轉子輪盤升速/降速幅頻特性曲線

比較β4=0(即無非線性剛度項)與β4=5×105m-2時輪盤1的一階諧波曲線,如圖9所示,可知非線性剛度使得轉子二階共振轉速發生了明顯的變化,但一階共振轉速變化相對不大。

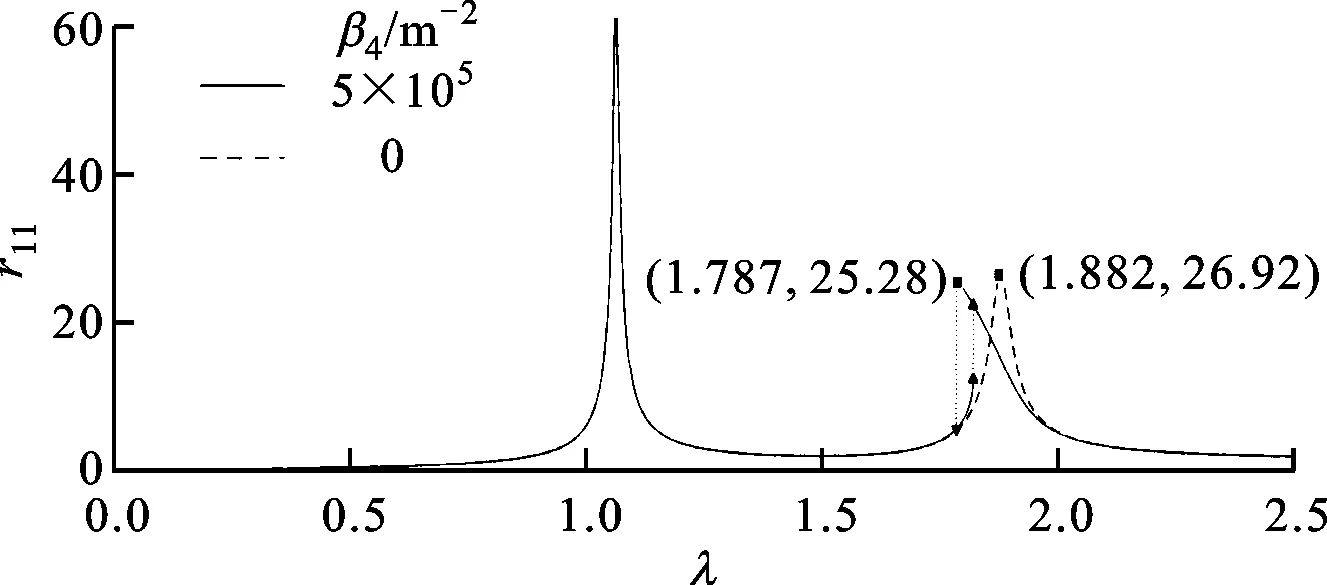
圖9 拉桿轉子輪盤1一階諧波對比曲線

圖8所示的無量綱幅頻曲線在λ<1時,三階諧波曲線的兩個共振峰分別對應一階、二階固有頻率的1/3次諧波。次諧波的出現表明三次方剛度模型受到非線性剛度項的影響表現出與線性模型不同的振動響應特性。一階、三階諧波曲線均可觀察到振幅突跳現象,但升速、降速曲線發生突跳的位置不同。這是因為動力學方程中存在非線性項,使同一轉速下的方程存在多解。

根據解的穩定性判斷方法[15],將解分為穩定解和不穩定解。不穩定解不能長期存在,因此隨著系統參數的變化,無量綱幅值作為微分方程組的解從單解區域進入不穩定區域(同樣也是多解區域)時,會發生從一個穩定解突跳至另一個穩定解的行為。由于系統控制方程只在特定的頻率范圍存在多解區域,在模擬升速或者降速時,由于進入多解區域時對應的頻率不同,使得振幅突跳位置不同。

3.3.2 結構參數對振動特性的影響 為分析系統響應出現的振幅突跳現象,有必要研究系統參數對解響應曲線的影響。取表2中參數,分別比較偏心量e、不平衡量夾角θ和無量綱阻尼系數ζ在不同取值下所對應的升速幅頻響應曲線,其余參數β2=β3=1,β4=5×105m-2。考慮到左右輪盤振動規律類似,非線性現象主要發生在系統二階固有頻率處,且二階、三階諧波相比一階諧波幅值過小,因此只繪制輪盤1的一階諧波在其第2階共振頻率附近的圖像。

模型轉子不同參數對響應曲線影響對比如圖10所示,可知增加偏心量e或兩輪盤間不平衡量夾角θ,減小無量綱阻尼系數ζ都會使得第2階共振峰向左方傾斜,并使多解存在的范圍擴大。

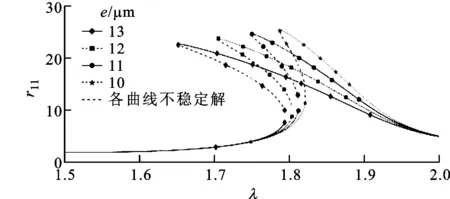
(a)偏心量的影響

(b)兩盤偏心距夾角的影響

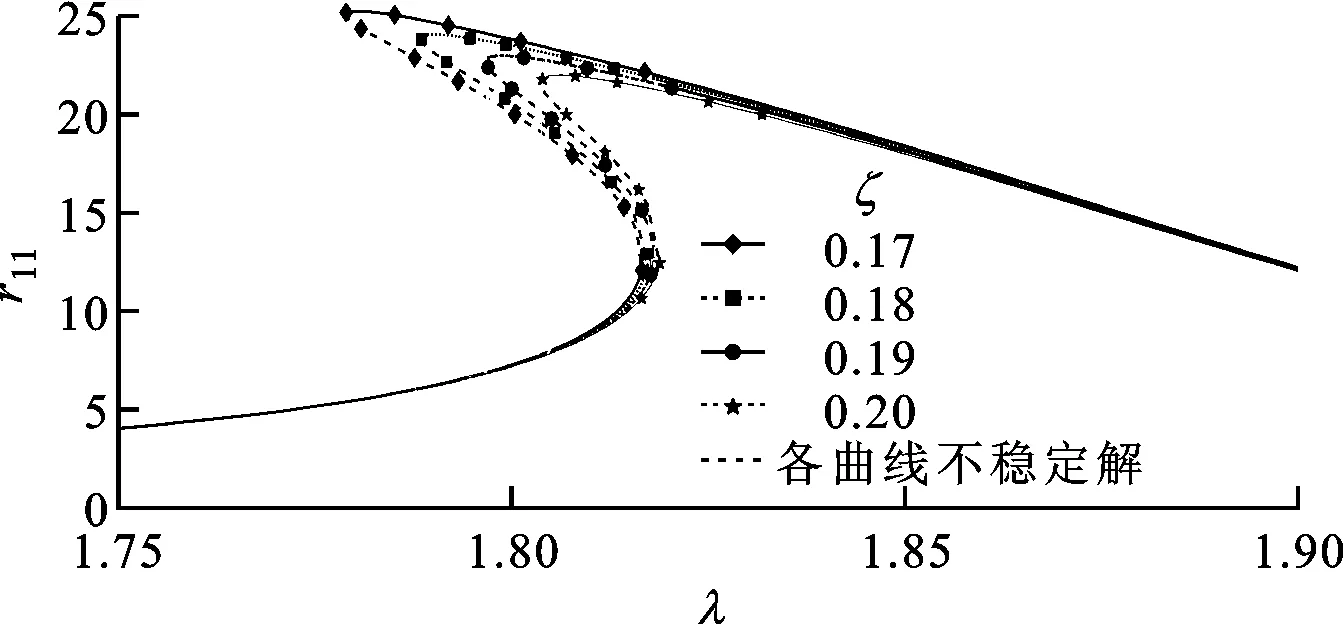
(c)無量綱阻尼的影響圖10 模型轉子不同參數對響應曲線的影響

不同質量比時輪盤1的幅頻響應曲線如圖11所示,計算參數取值見表3,其余參數θ=90°,β2=1,β3=1。由圖11中可知,增加質量比會使轉子系統第1階、第2階固有頻率減小。輪盤1第2階無量綱共振幅值隨質量比增加而增大。輪盤2對應無量綱幅頻曲線由于篇幅所限未展示,但其共振時無量綱幅值變化規律與輪盤1相反,第2階無量綱共振幅值隨質量比的增加而減小。

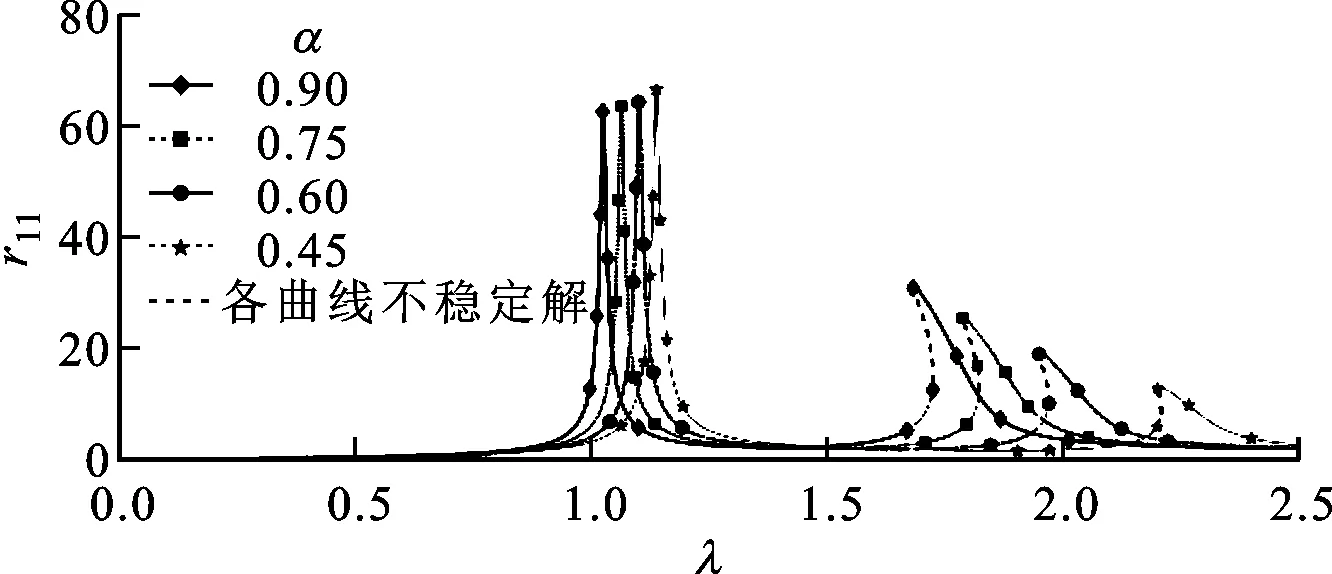
圖11 不同質量比時輪盤1的幅頻響應曲線

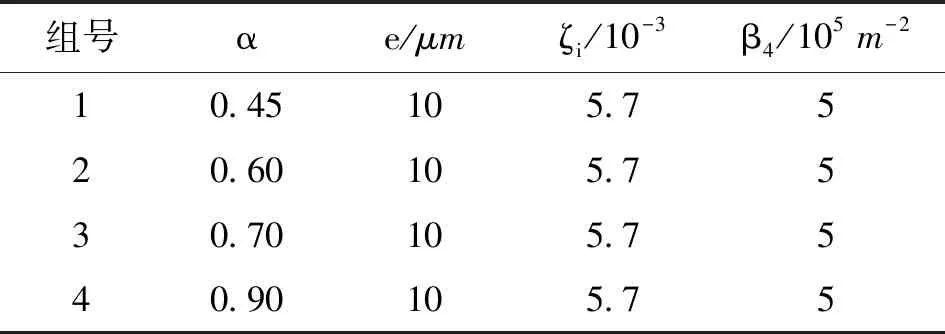
組號αe/μmζi/10-3β4/105 m-210.45105.7520.60105.7530.70105.7540.90105.75

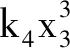
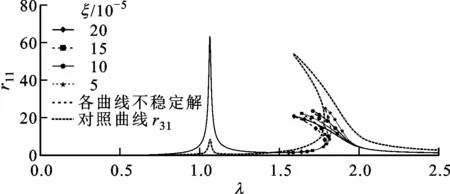
圖12 非線性剛度占比對輪盤1幅頻響應曲線的影響

共振峰的偏移使系統存在多解的頻率范圍擴大,進而使振幅不穩定區域擴大。減小輪盤偏心量,兩盤偏心量夾角和非線性剛度占比,或者增加無量綱阻尼均能縮減雙穩態的存在區域;而改變兩輪盤之間的質量比,則能夠改變振幅突跳發生的位置。

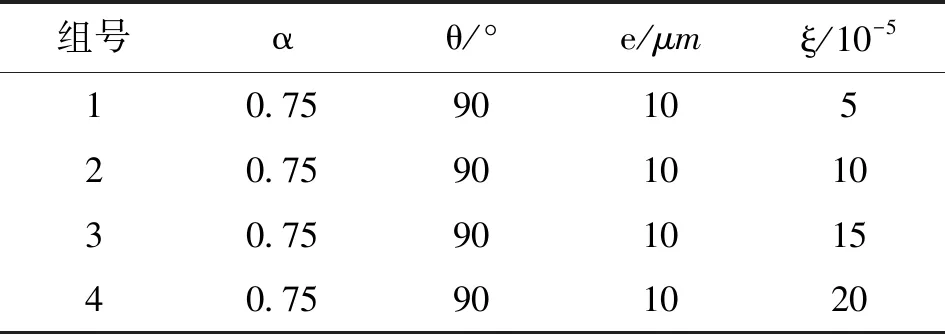
表4 對比ξ時轉子系統的參數取值

3.3.3 結構參數影響分析 結構參數對系統響應的影響結果可從能量和非線性剛度影響作用強弱的角度進行分析。

(1)由式(15)可知,增加偏心量e相當于增加非線性剛度占比ξ,同時具有減小拉桿剛度的作用。隨著偏心量增加,非線性剛度影響增大但總剛度減小,輪盤1的響應曲線不穩定區域即解的雙穩態區域變大,第2階固有頻率減小。

(2)增加不平衡量夾角會使兩輪盤的位移差即(r1-r2)增大,進而使得非線性剛度k4(r1-r2)3增大,使輪盤1二階固有頻率處解存在的雙穩態區域擴大。

(3)在外部輸入能量不變的情況下,增加無量綱阻尼系數ζ使系統在一個周期內被阻尼消耗的能量增加,因而系統響應幅值減小。

(4)由式(15)可知,增加質量比α相當于增加輪盤1的質量比,解曲線的振幅增加而各階固有頻率減小。

4 雙線性剛度模型

隨著輪盤相對位移的變化,圖4中關系曲線可分成斜率不同的兩個部分,變化規律可近似用兩段斜率不同的直線表示。假設拉桿和接觸面的等效剛度隨拉桿的伸長呈線性變化,則對應的回復力為

F(s)=κs

(22)

式中κ、s分別為拉桿、接觸面的等效剛度和拉桿的伸長量。

固定輪盤1,接觸段的橫向剛度為

(23)

式中:sx為輪盤2的位移在x方向上的投影;F(s)為拉桿受到的拉力。

轉子受到載荷發生彎曲,拉桿變形的形態如圖13所示,用一條折線近似描述拉桿的變形。拉桿伸長在x方向上的投影為

(24)

式中:θ1、θ2分別為彎折前、后拉桿與z軸的夾角;scr為發生彎折時拉桿的伸長量。

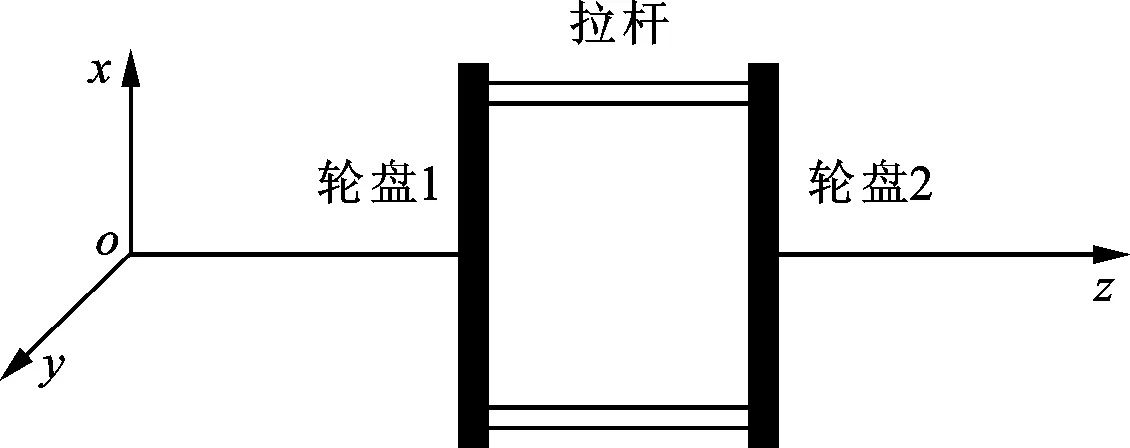
(a)未受載荷時接觸部位

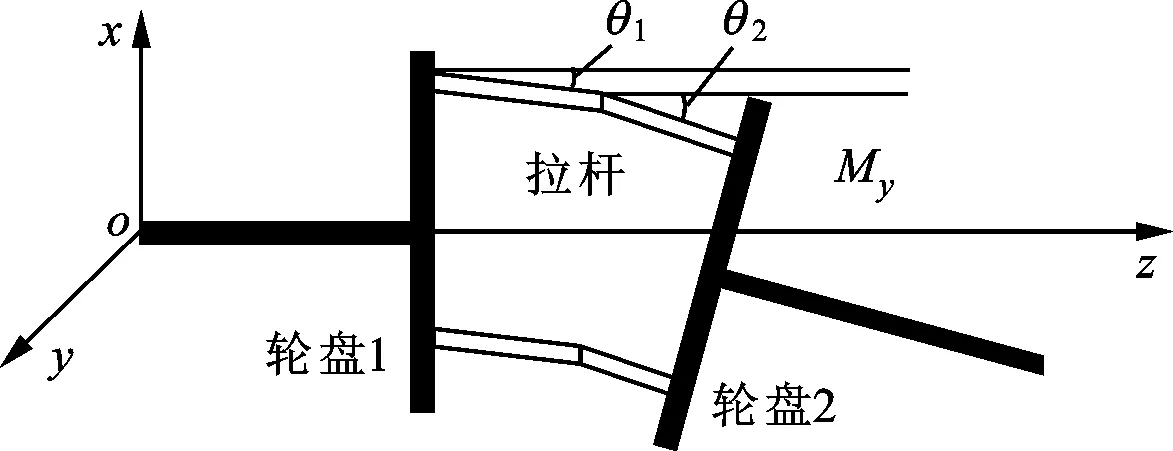
(b)受外載荷時拉桿彎曲示意圖圖13 拉桿受載荷變形示意圖

將式(22)(24)代入式(23)可得

(25)

用x代替sx表示輪盤的橫向位移,由式(24)可知等效橫向剛度呈雙線性,結果如圖14所示。與有限元剛度計算結果對比可知,兩個模型等效回復力曲線相符合,雙線性模型可近似反映剛度的變化趨勢,圖14中兩斜率關系為kl2=0.8kl1。

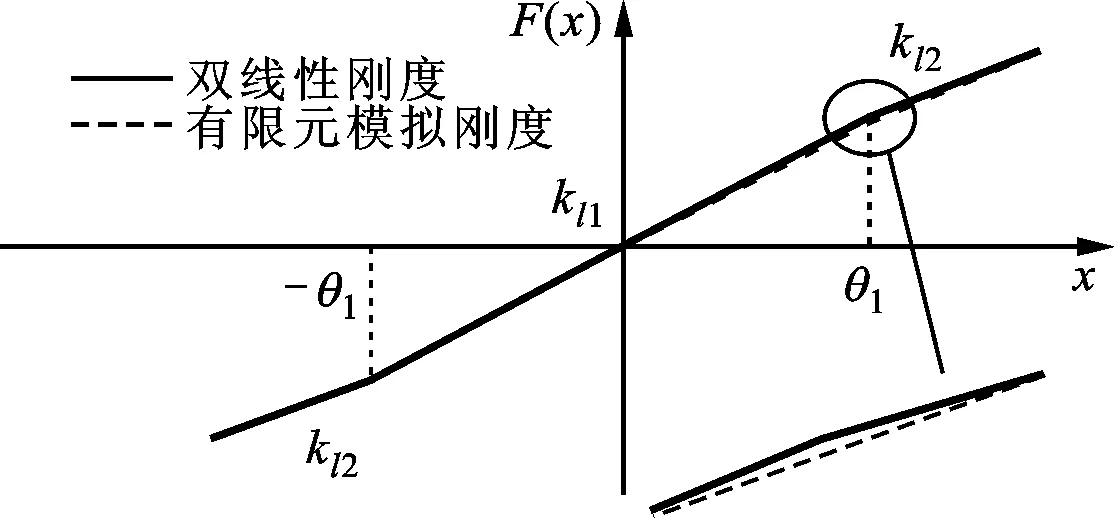
圖14 雙線性剛度及與有限元模擬剛度對比

4.1 雙線性剛度模型動力學方程

設xcr為拉桿發生臨界彎折時在x方向上的伸長量,則

xcr=scrsinθ1

(26)

記單個圓盤各方向的橫向剛度為

(27)

將式(23)(24)代入式(14),得到雙線性模型的控制方程組

(28)

定義函數

(29)

式中:rcr=xcr/e為拉桿彎折時的無量綱閾值;βli=kli/k1(i=1,2)為等效剛度與輪盤1剛度的比值;γ=βl2/βl1為彎折前、后剛度的比值。

4.2 轉子穩態響應行為分析

取不同轉速Ω,并使用4階龍格-庫塔方法求解式(28),記錄穩態響應幅值。取無量綱阻尼系數ζ1=ζ2=ζ3=0.01,α=0.75,γ=0.7,rcr=10,β2=βl1=1,計算得到無量綱幅頻曲線,如圖15所示,可知雙線性模型無量綱幅頻曲線中同樣出現了振幅突跳現象。輪盤2的無量綱幅頻響應曲線與輪盤1的類似。

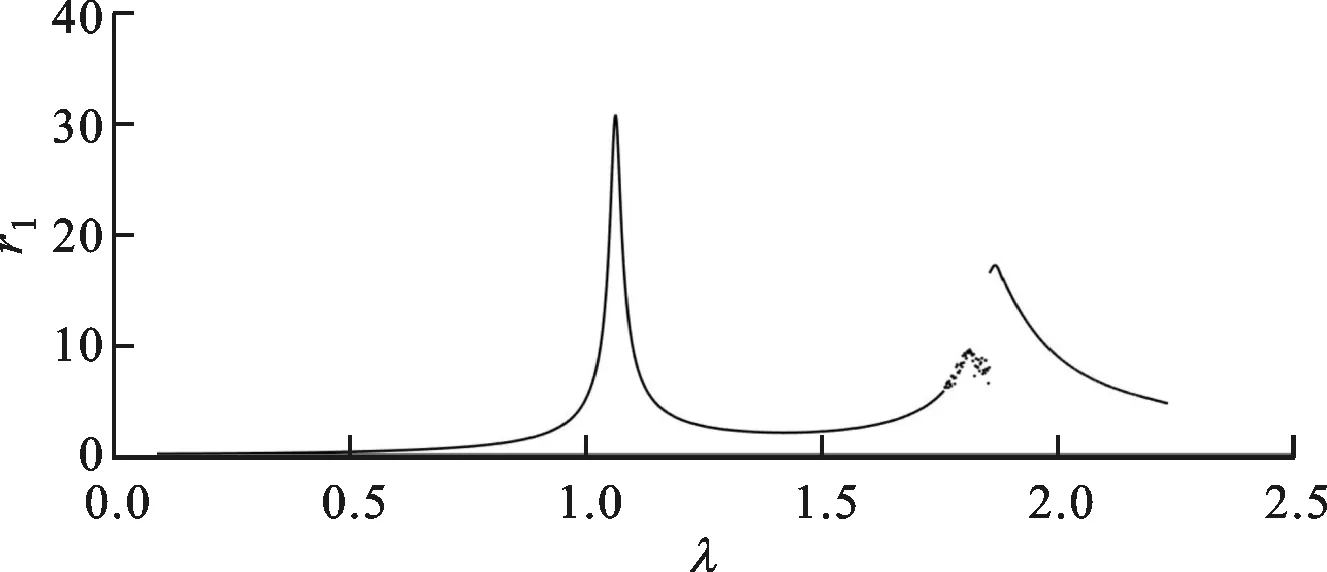
圖15 轉子雙線性模型輪盤1幅頻響應曲線

無量綱幅頻響應曲線中出現的振幅突跳現象由剛度突變造成。當r1與r2的差值接近rcr并且不斷增大時,響應曲線先是經歷了一個振蕩區域,在此范圍內,無量綱振幅變化無明顯規律;然后無量綱振幅突然增加,通過第二節臨界轉速后,隨著轉速增大,無量綱幅值表現出規律性的減小,如圖16所示,λ取值為1.76～2.20。兩輪盤位移差值隨轉速變化圖如圖17所示,可知當無量綱差值為9.17接近xcr時,響應曲線開始變得不穩定。

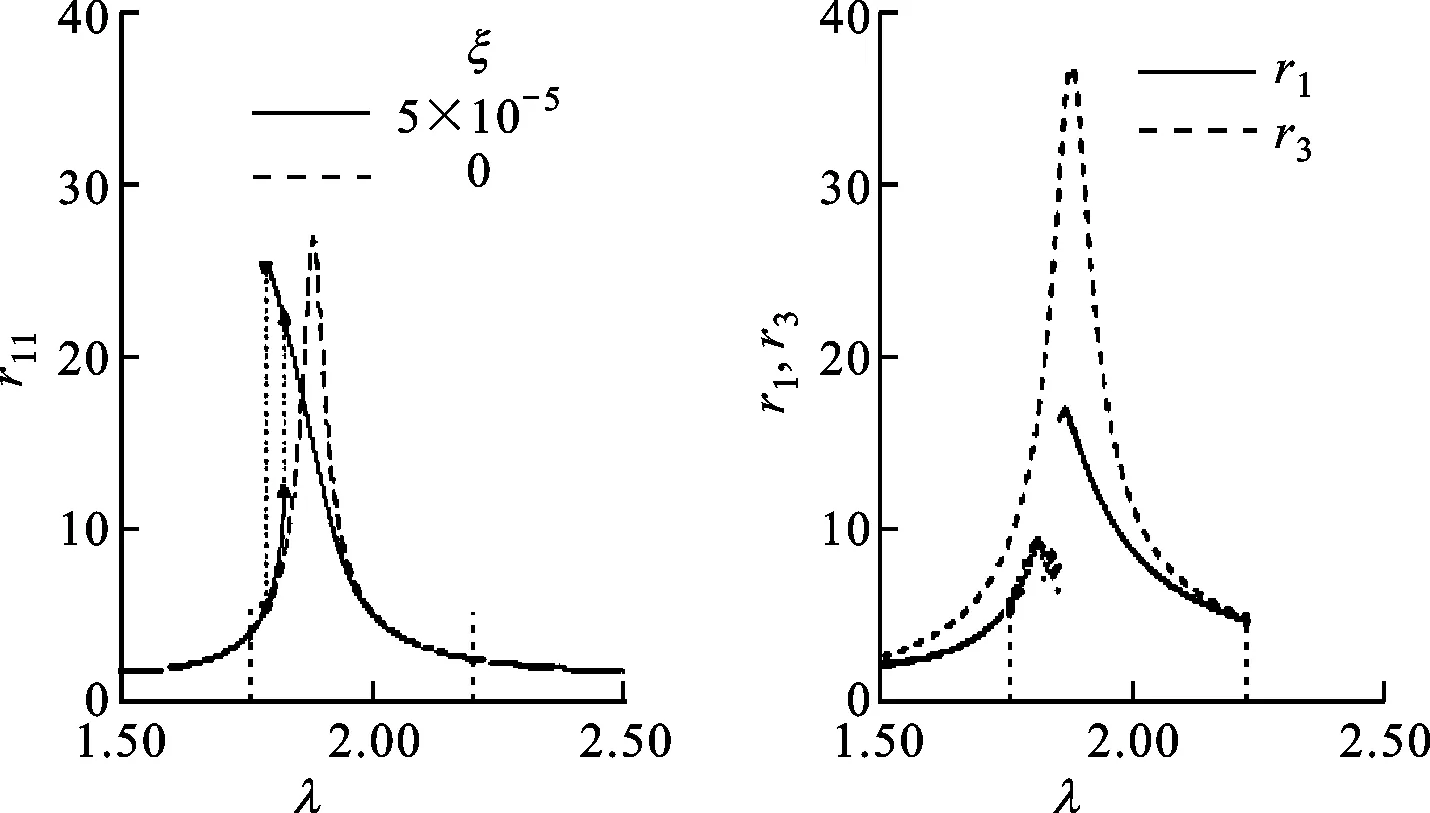
(a)模型1雙穩態區域 (b)模型2不穩定區域圖16 兩模型不穩定區域對比

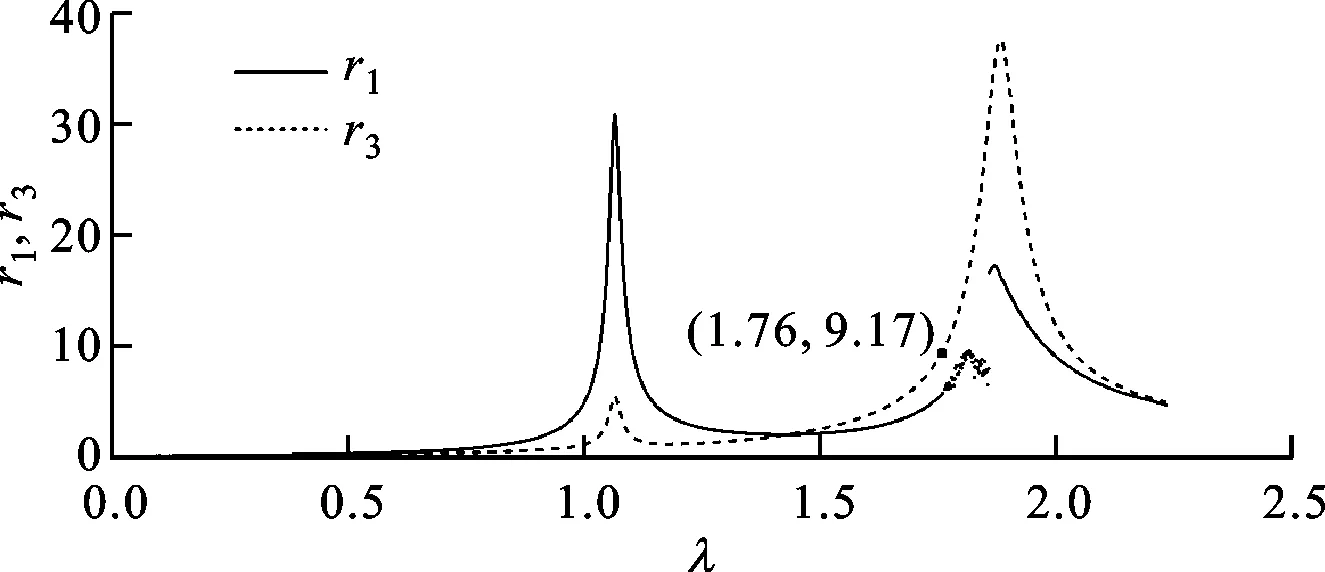
圖17 兩輪盤位移差值隨轉速變化圖

4.3 三次方剛度模型與雙線性剛度模型對比

采用三次方剛度模型和雙線性剛度模型對有限元計算結果進行近似并分析其非線性響應,計算結果均表現出振幅突跳現象,且突跳位置基本相同。兩模型差別和聯系在于:三次方剛度模型的升速和降速幅頻曲線振幅突跳發生的位置不同,而兩個突跳之間的頻段是振幅的雙穩態區域。對比兩個模型的計算結果得出結論:轉子系統剛度非線性變化是影響振幅突跳和致使系統不穩定的原因。

5 結 論

本文利用三次方剛度模型和雙線性剛度模型近似拉桿和接觸面等效橫向剛度,分別建立了轉子動力學模型,并對兩種模型的計算結果進行對比,得到如下結論。

(1)兩種近似模型均能模擬拉桿轉子的非線性動力學特性,并反映出組合式轉子在工作中發生的振幅突跳現象。

(2)三次方剛度模型的幅頻曲線,振幅突跳原因是動力學方程在一定頻段存在多解,且存在諧波響應;但其升速和降速幅頻曲線發生振幅突跳的位置不同,兩突跳之間的區域即雙穩態區域。雙線性模型中,振幅發生突跳在于剛度發生了突變,并在此之前經歷一個不穩定區域,該區域對應前一模型的雙穩態區域。

(3)減小輪盤偏心量e、兩盤偏心量間的夾角θ,或者增加無量綱阻尼系數ζ,均可使解響應曲線的不穩定區域減小,而改變輪盤質量比α,則能夠改變此不穩定區域的位置。通過調整系統參數,能有效避免轉子系統在不穩定的頻率范圍內工作。