基于空間滯后模型的出租車需求影響因素分析

張自荷 王 振 吳 瑞

(長安大學公路學院1) 西安 710064) (北京交通發展研究院2) 北京 100161)

0 引 言

出租車是城市公共交通系統的重要組成部分[1].現階段，出租車行業在空間區域面臨需求與供給不匹配的問題[2]，因此，對不同城市區域的出租車需求量進行精準預測對提高出租車服務水具有十分重要的意義.需求量預測的常用方法有原單位法、增長率法、聚類分析法、函數法和回歸分析法.當自變量和因變量等相關數據可以準確獲取時，回歸分析可以很好得對未來出行量進行預測[3].出租車GPS數據作為地理空間活動記錄數據，包含了車輛的設備狀況、運營狀態、地理位置信息、瞬時速度以及運行方位角等信息[4]，現已被用來進行交通狀態的估計[5]、交通行為分析[6]、出行OD預測[7]和出行時間預測[8]，但目前較少研究關注利用出租車GPS數據研究高峰時期的出租車需求，且建模過程中未考慮需求在空間上的依賴關系和聚集現象.

綜上，文中基于出租車GPS數據，通過提取上車點獲得基于交通小區的出租車需求，構建空間回歸模型，研究高峰時期出租車需求的影響因素并對結果進行討論，為城市公共交通系統優化、高峰時期出租車需求量預測等提供方法支撐和研究途徑.

1 數據預處理

1.1 GPS數據預準備

出租車GPS數據由車載終端生成，通常為每隔15～60 s采集一次數據信息并采用及時通信方式上傳至數據中心的數據庫中.本文所采用數據為西安市2017年4月17日繞城高速范圍內的出租車GPS數據，所選日為星期一，天氣晴朗，無重大節假日，因而保證了數據所具有的代表性.數據包含信息中與本研究相關的包括車牌號、經度、緯度、GPS時間、車輛載客狀態，其形式見表1.

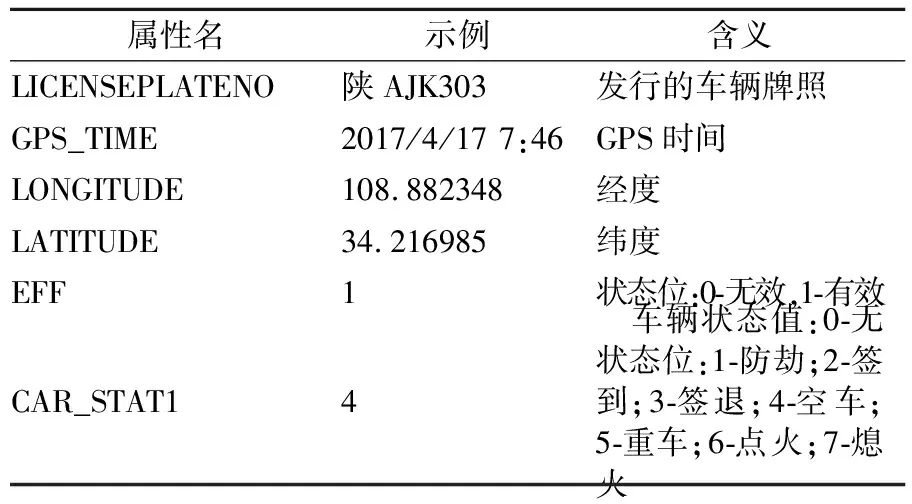
表1 與本研究相關的出租車GPS數據結構

出租車交通行為由多個在時空上連續的GPS軌跡點組成，構成車輛的行駛軌跡，并可反應車輛上、下客活動信息[9].本文研究的是出租車需求的影響因素，因此，首先需要從一系列軌跡點中提取上車點的經緯度信息以確定出租車上客點在空間上的數量與分布.以西安市出租車GPS為例，具體提取步驟如下：①數據清洗，刪除狀態位無效，存在數據錯誤或缺失，車輛狀態值為0，1，2，3，6，7的記錄；②數據排序，按車牌號聚類并按時間升序排列；③上下車點提取，將車牌號相同的由持續的車輛狀態值為4轉變到狀態值為5和緊鄰的持續狀態值為5轉變到狀態值為4的兩點提取出來，將此兩點認為是一次完整出行的上、下客點.

通過上述提取步驟，獲得繞城高速區域內11 634輛營運出租車的356 972條行程數據，其全天上客點隨時間的分布見圖1，其中早、晚高峰時段(參照相關研究，本文早高峰時段確定為07：00—09：00，晚高峰確定為18：00—20：00出行量分別為32 420次和35 162次，占比為9.1%和9.9%，全天平均小時出行量為14 874次.考慮現有研究未涉及到高峰時段出租車出行量影響因素且晚高峰出行量較高，故選擇晚高峰時段作為研究對象.

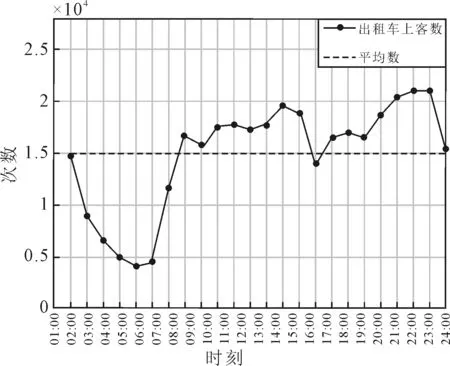
圖1 繞城高速范圍內出租車出行量的時間分布

1.2 地圖匹配

地圖匹配是指在ArcGIS軟件中通過一致坐標系下的空間位置關系將出租車上客點連接至路網線地理文件和交通小區面地理文件，其中，交通小區是用來預測出行產生和吸引的最基本的分析單元，通常包含人口數量、工作崗位數量、機動車擁有量等屬性信息，本研究中將西安市繞城高速范圍內區域劃分為601個交通小區，每個小區內包含2011年西安市綜合交通調查獲取的常駐人口、賓館流動人口、崗位數、小汽車擁有量等屬性數據.通過統計晚高峰時段落在各交通小區內部的上客點數量獲得各小區的晚高峰出租車需求[10]，見圖2.

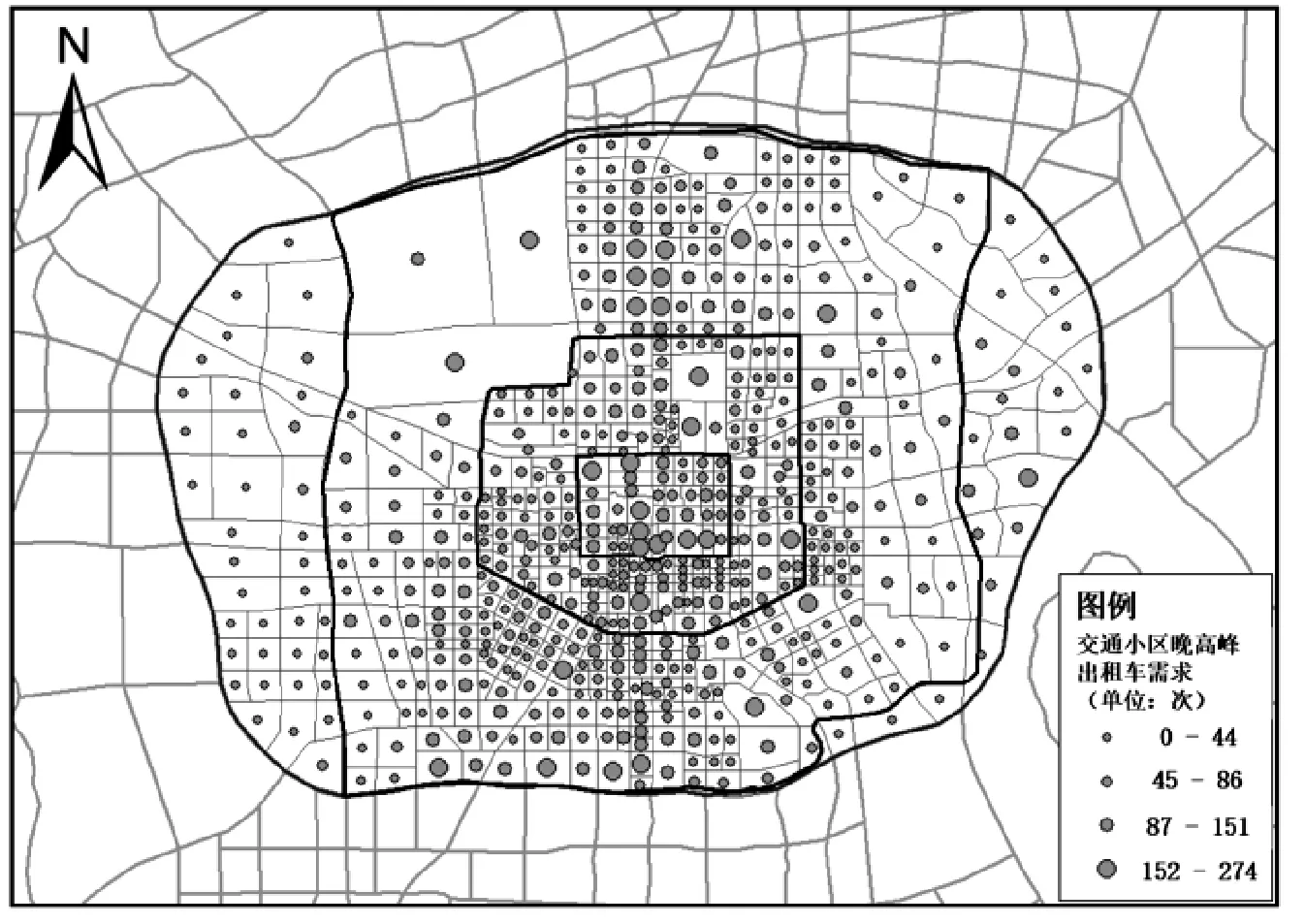
圖2 交通小區晚高峰出租車需求空間分布

2 出租車需求影響因素分析

2.1 出租車需求相關影響因素分析

出租車需求預測可分為短期預測和中長期預測[11].中長期預測用于出租車宏觀管理和規劃，短期預測為出租車實時調度提供依據，本文主要研究的是出租車中長期出行預測.綜合已有文獻，影響出租車中長期需求的影響因素包括，總人口數量、就業人口數量、小汽車擁有量、性別占比等區域人口屬性；通勤出行時間、出行目的等出行特征[12]；商業區面積、居住區面積等土地利用特征[13]；停車場供給，公共車供給，地鐵供給，自行車道密度等其他交通方式供給特征等因素.

2.2 地鐵可達性指標構建

公交車供給和地鐵供給這兩個影響因素，通常通過可達性進行量化，即對于某個目的點來講，乘坐公交車的便利程度.可達性由可達性指標表征，通常與到達該點車輛頻次、車站距離目的地的步行時間等影響因子有關，然而，由于很難獲得整個城市的具體公交車頻次信息，現有研究多只計算特定區域內公交可達性指標.考慮到數據可得性，本文僅計算各交通小區的地鐵可達性指標(metro access time, MAT)，借鑒文獻[3]對公交可達性指標的定義方法，本文將其定義為每個交通小區的質心到距離最近地鐵站的步行時間加上地鐵等待時間，其中，步行速度取4 km/h，等待時間按發車間隔時間的1/2計算，為

(1)

式中：f為每小時的地鐵發車頻次；D為基于拓撲路網的交通小區質心到最近地鐵站的步行距離；Vw為步行速度.地鐵可達性越高，地鐵可達性指標(MAT)越小.

2.3 數據準備與變量定義

選用的潛在自變量及變量解釋見表2.受城市布局和功能結構影響，出租車需求在某些交通小區較高，而在某些交通小區較低，因此，研究區域內基于交通小區的晚高峰出租車需求直方圖呈現偏態分布，見圖3.為滿足后續建立線性回歸模型的因變量正態分布假設前提，將因變量進行對數轉換，結果見圖4.為保持與因變量的一致性以更好表征兩者間的線性關系，各潛在自變量也做相應對數變換.

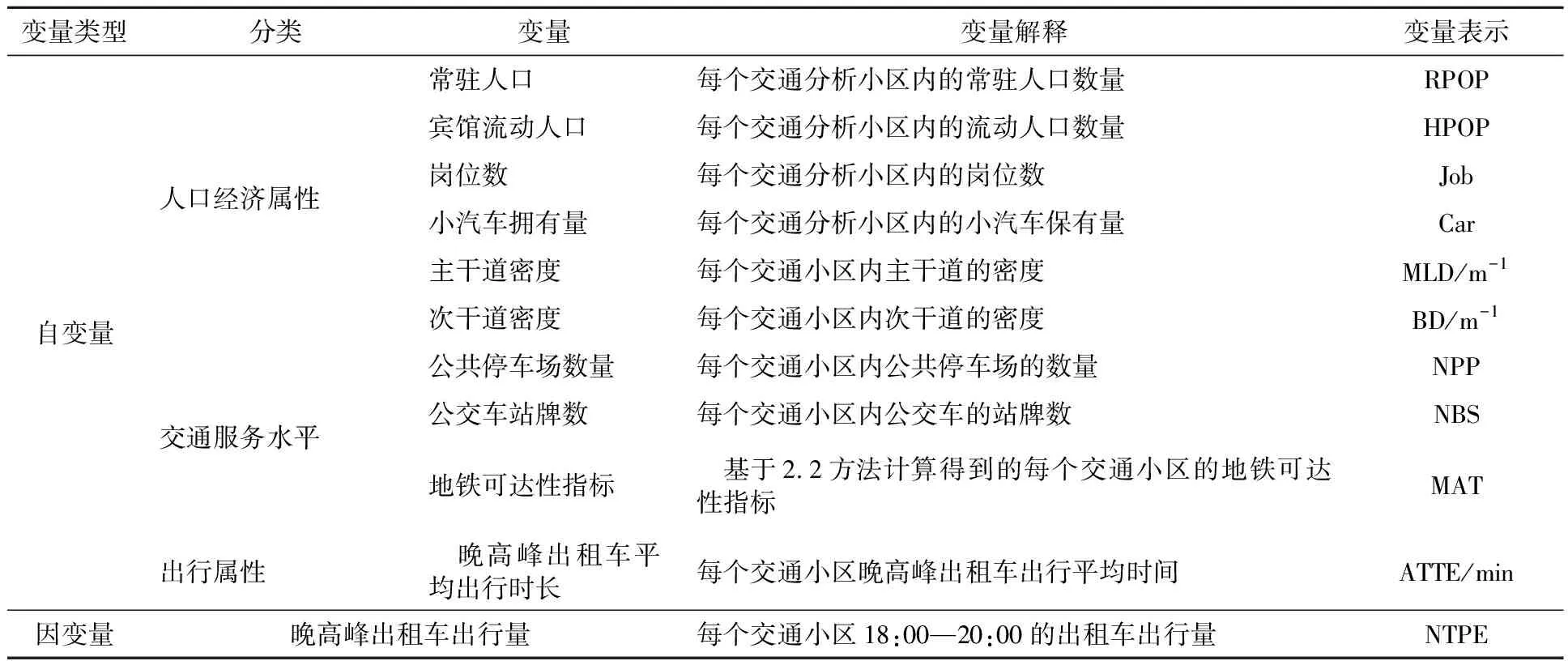
表2 潛在自變量和潛在因變量的定義

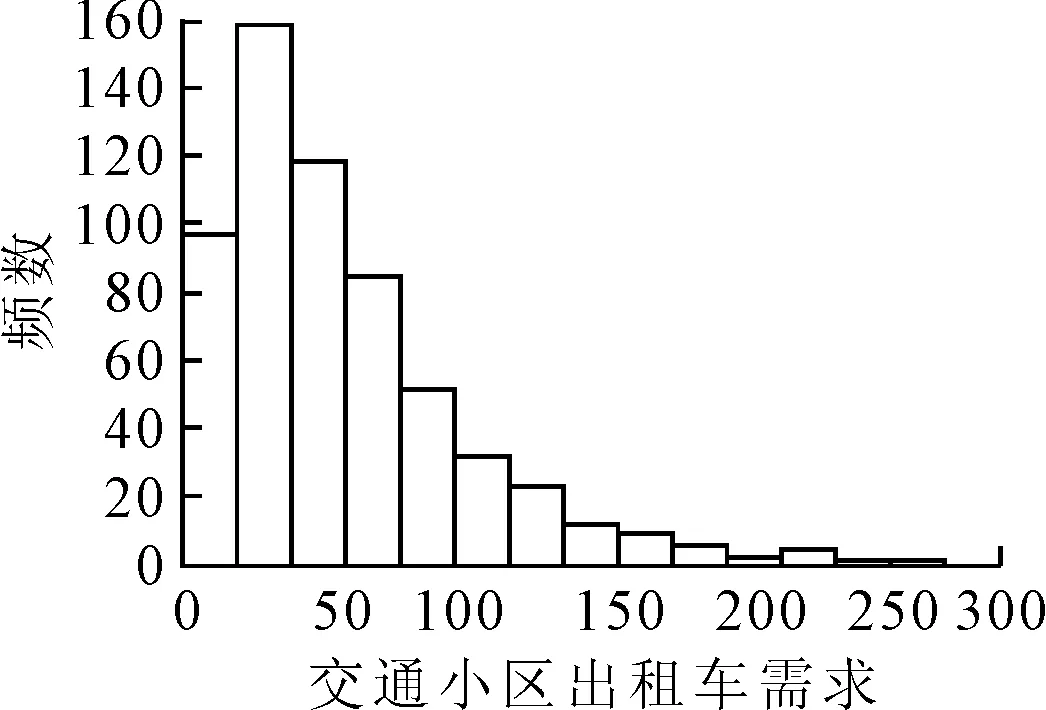
圖3 晚高峰出租車需求直方圖

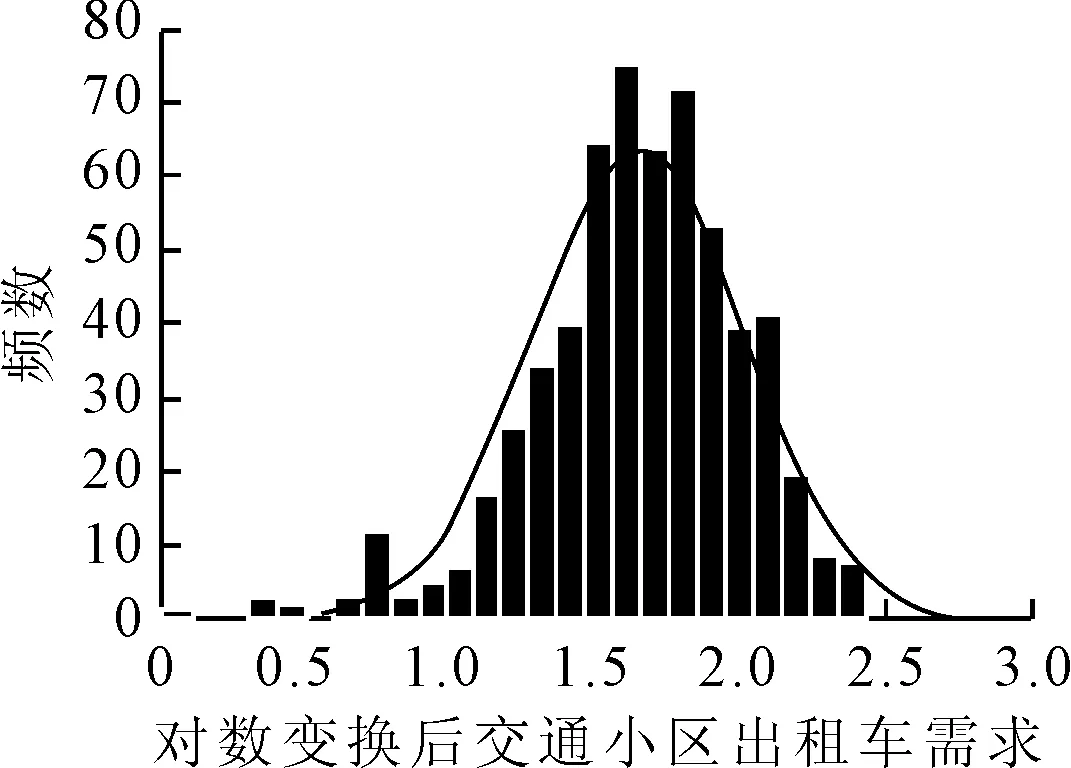
圖4 對數變換后晚高峰出租車需求直方圖

3 考慮空間自相關的出租車影響因素建模

3.1 全局空間自相關

通過晚高峰出租車上車點可視化結果，可以看出某交通小區晚高峰出租車需求與鄰近交通小區晚高峰出租車需求相關，即以交通小區為單位的出租車需求具有空間相關性，若基于統計學和傳統計量經濟學理論對此類存在空間相關性的樣本進行建模，將會導致較大的方差估計、較低的假設檢驗顯著水平和較低的擬合度，因此，需要對此類數據進行空間相關性檢驗.通過構建全局Moran’s I指標檢驗出租車需求在統計學上是否具有空間集聚特征，計算式為

(2)

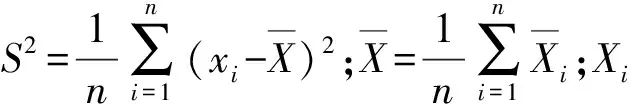
(3)

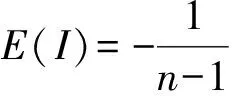
根據各交通小區的空間關系構建空間權重矩陣，利用Geoda軟件計算得到晚高峰各交通小區出租車需求的全局Moran’sI指數為0.440，檢驗的Z值為20.025，表明在1%的顯著水平上通過了檢驗，即晚高峰期間出租車需求在空間上是正相關的.

3.2 空間滯后模型建立

由于晚高峰出租車需求在研究區域是空間正相關的，因此對其建模時，應充分考慮因變量在空間上不獨立這一前提，將地區間的相互關系引入模型，采用基于空間權重矩陣對傳統線性線性回歸模型進行改進的空間計量模型進行模型構建.空間計量經濟模型根據經濟活動的空間相依性和回歸模型中的誤差項的相依性特征基本分為兩類模型：空間滯后模型和空間誤差模型，而這兩類模型的構建的都是以相應的線性回歸模型為基礎的，因此，本文首先對各影響因素變量與因變量之間的相關性和各影響因素之間的相關性進行檢驗，篩選出進入回歸模型的潛在自變量.其次，建立普通線性回歸模型并構建判別指標選出適合的空間計量模型.最后，建立空間計量模型，利用最大似然法對系數進行估計，將回歸結果與普通最小二乘法的回歸結果進行比較，分析變量的系數變化及擬合度差異.

3.2.1潛在自變量的篩選

由于潛在自變量較多，為避免無效變量進入模型，先對各潛在自變量進行初步篩選，從而選出進入回歸模型的自變量.考慮到本研究中各自變量均為數值型變量，采用皮爾遜相關系數矩陣計算出各潛在自變量與因變量之間的相關系數，通常，統計顯著情況下相關系數絕對值大于0.5被作為潛在自變量進入模型的依據，為避免遺漏晚高峰出租車需求的有效影響因素，本文采用在0.01顯著水平下相關系數的絕對值為0.2作為潛在自變量進入模型的臨界值.為避免自變量之間的共線性導致的回歸模型系數有偏估計，本文在上步篩選基礎上計算了擬進入模型變量兩兩之間的相關性系數，相關性系數大于0.7的變量中至多有一個能進入模型.

根據上述原則構建皮爾遜相關系數矩陣對潛在自變量進行篩選，結果表明，賓館流動人口、公共停車場數量、公交車站牌數和地鐵可達性與因變量在0.01顯著性水平下的相關性系數分別為0.204，-0.239，0.525和0.219，且四個潛在變量兩兩之間的相關系數均小于0.7，因此，選擇以上四個變量作為進入普通線性回歸模型的變量.

3.2.2空間計量模型的建立

1) 普通線性回歸模型的建立 空間計量模型是以普通線性回歸模型為基礎建立的，因此，首先構建如下普通線性回歸模型：

(4)

式中：Yi為各交通小區中晚高峰出租車需求；Xi為第i個解釋變量；n為自變量的個數，在初始模型中n= 4；a0為模型的截距；ai為對應與Xi的系數.采用最小二乘法對變量系數進行估計，即當觀測變量與預測變量間的殘差平方和最小時，所得系數為系數估計值.此外，為獲得解釋度更高的模型，采用逐步回歸的方法對初步篩選出的變量進行二次篩選，其優點在于每向模型中引入一個變量，均要考察原來在模型中的自變量是否統計顯著，若否，則將變量剔除.

模型的回歸結果見表3，模型的擬合優度為0.468，且各變量在0.001的統計水平下顯著.變量公共停車場數量和變量公交車站牌數的系數分別為0.544和0.219，表明這兩個變量對出租車需求的影響均為正向的.變量地鐵可達性指標的系數為-0.218，結合前述地鐵可達性指標算法可知，該指標越小，地鐵可達性越高，因此，地鐵可達性越高的地方相應的出租車需求也越高.從模型的總體結果來看，與停車場、地鐵和公交車服務供給越多的地方，出租車需求越少的預期相反，其他機動車方式越便捷的區域，出租車需求也相應越高，這可能與兩個原因相關：①公共停車場、地鐵和公交車服務供給較多的區域，通常出行需求也較旺盛；②出租車因其靈活的出行方式，可作為其他交通方式的接駁以完成基于“門到門”的出行過程.

由于各交通小區的出租車需求為空間變量，為檢驗普通線性回歸模型的殘差中是否存在未解釋成分，對其殘差進行空間自相關檢驗，結果表明，Moran’sI統計值為0.360，相應的Z得分為16.354，即在0.01顯著性水平下，拒絕殘差不具有空間自相關性的原假設.這說明普通線性回歸模型對因變量的未解釋部分是未考慮因變量之間的空間相對關系造成的，因此，需要建立空間模型來解釋出租車晚高峰需求.

2) 空間模型選擇 空間滯后模型和空間誤差模型作為兩種基礎的空間計量模型，充分考慮了變量之間的空間交互效應，其區別體現在空間滯后因子的構成上.在空間滯后模型(spatial lag model，SLM)中，空間滯后項由空間權重矩陣與因變量乘積構成，作為模型右側的解釋變量之一；

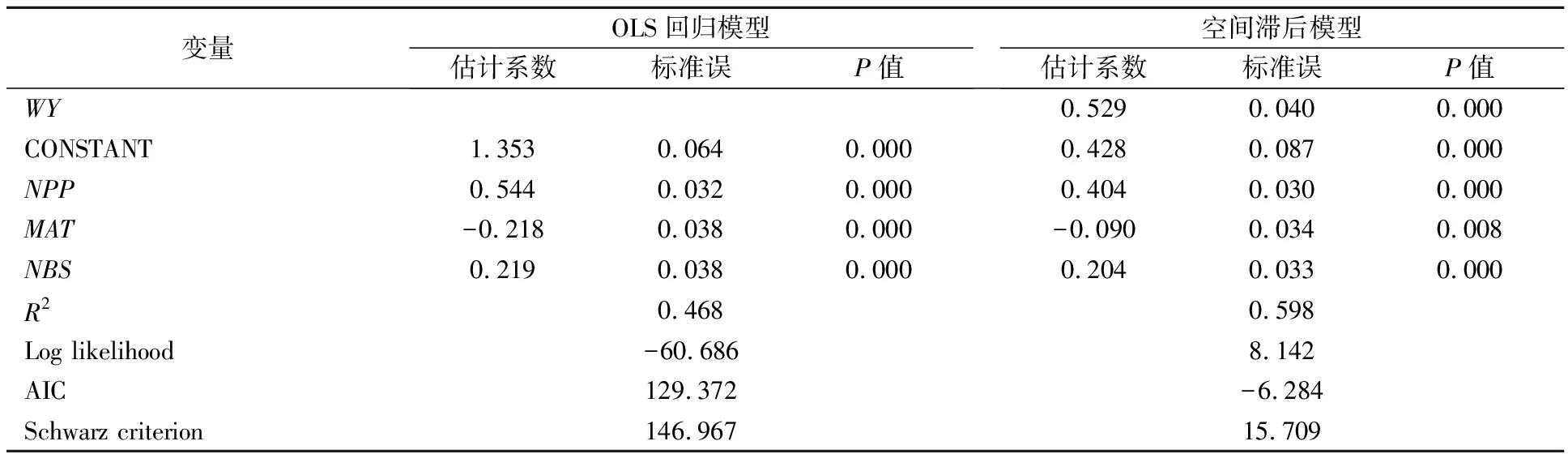
表3 模型估計結果

在空間誤差模型(spatial error model，SEM)中，空間滯后項由空間權重矩陣與誤差項乘積構成，作為誤差項的解釋變量，但不作為因變量的解釋變量.構建兩個拉格朗日乘數(Lagrange multiplier)形式LMERR、LMLAG及其穩健的R-LMERR、R-LMLAG來實現空間滯后模型與空間誤差模型的選擇，Anselin 等[14]給出的判別準則：若在空間效應的檢驗中發現當LMLAG較之LMERR在統計上更加顯著，則選擇空間滯后模型較為合適；相反，若LMREE比LMLAG在統計上更加顯著，且R-LMERR顯著而R-LMLAG不顯著，則選擇空間誤差模型較為合適.表4為基于普通線性回歸模型的空間效應檢驗結果，由兩類拉格朗日乘數檢驗可以看出，LMLAG較LMERR在統計上顯著，且R-LMLAG在0.01水平下顯著而R-LMERR不顯著，因此空間滯后模型更適合擬合出租車晚高峰需求.

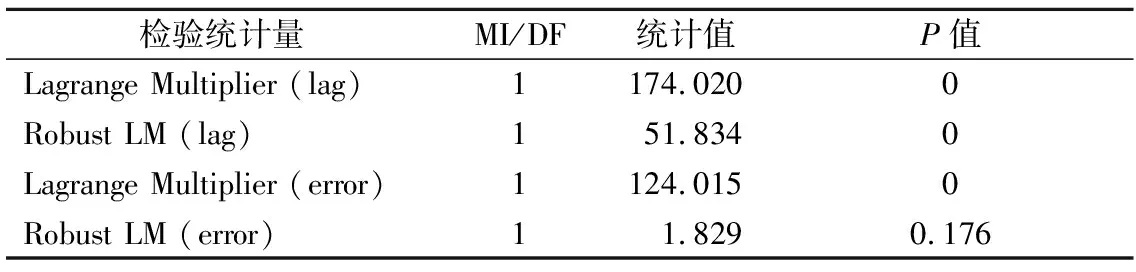
表4 晚高峰出租車需求的空間效應檢驗

3) 空間模型的建立及分析 針對晚高峰出租車需求的空間滯后模型為

Y=ρWY+Xβ+ε

(5)

式中：Y為N×1維因變量向量；X為包含解釋變量公共停車場數量，地鐵可達性和公交站點數量的N×3維向量；WY為前述的空間滯后因子；ε為N×1維誤差向量；W為N×N維空間權重矩陣，與前述空間自相關時建立的權重矩陣相同，β為解釋變量的系數；ρ為空間自相關系數；N=601為研究區域內交通小區的數量.假設誤差服從均值為零，方差為σ2的獨立同分布，且與解釋變量X不相關，即E(X′ε)=0.當空間自相關效應存在時，空間滯后項的系數ρ≠0, 即出現變量的內生性問題，普通最小二乘估計將不再適用,因此本文采用最大似然估計法(ML)對各自變量的系數進行估計.

利用Geoda軟件得到的空間滯后模型的估計結果見表3.由表3可知，模型的擬合優度指標R2由0.468提高到0.598，對數似然值Log likelihood有所增大，同時，從赤池信息準則和施瓦茨準則看，模型的AIC值和SC值都有所下降，且空間滯后項 的系數在0.01水平下顯著，因此，空間滯后模型的整體擬合效果較好.從模型的系數估計結果看，所有系數均在0.01水平下顯著，空間滯后項的系數為0.529，表征當某個小區的出租車需求較高時將會對與它有共同邊或節點的臨近交通小區的出租車需求產生正向的影響，即出租車需求具有區域溢出效應.此外，引入空間滯后項后，各變量的系數雖符號未變，但其絕對值都較未引入前有所減少，表明晚高峰某交通小區的出租車需求不僅與這一交通小區內的公共停車場數量、地鐵可達性和公交車站牌數均成正向關系，也與周邊交通小區的出租車需求有很大的正向關系.

4 結 論

1) 在對出租車GPS軌跡數據進行預處理的前提下，提取上客點的地理位置，通過統計落在各交通小區的上客點數量，得到了各交通小區晚高峰時段的出租車需求.

2) 晚高峰出租車需求的全局空間自相關檢驗結果表明，晚高峰期間出租車需求在空間上是正相關的，因此將其作為因變量進行建模時應充分考慮其在空間上不獨立這一特征.

3) 空間滯后模型的估計結果表明，空間滯后項在0.01統計水平下顯著，且其整體擬合效果優于普通線性模型，因此，空間滯后模型能更好的對晚高峰出租車需求進行擬合.

4) 晚高峰出租車需求與地鐵可達性、公共汽車站數量、公共停車場數量均成正相關，且考慮空間因素后，這些變量對出租車晚高峰需求的影響有所降低.