Variational Problem of One Power Type Functional about Second Fundamental Form

Liu Jin

(College of Systems Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract For an n-dimensional submanifold in a general real ambient manifold φ:Mn→Nn+p， let S denote the square length of second fundamental form of φ. In this paper, we introduce one power type functional concerning S as where r≥1 is a real number, which measures how derivations φ(M) from a totally geodesic submanifold and has a closed relation with the well known Willmore conjecture. For this functional,the first variational equation is obtained, and in unit sphere,we construct a few examples of critical points. Moreover, by two famous matrix inequalities, we derive out the Simons’ type integral inequalities, and based on which a gap phenomenon has been classified.

Key words Second fundamental form Willmore conjecture Critical point Simons’ type integral inequality Gap phenomenon

1 Introduction

Letφ:Mn→Nn+pbe ann-dimensional compact without boundary submanifold in a general ambient manifold. Sometimes we chooseNn+pto be (n+p)-dimensional space formsRn+p(c). It is well known that whenc=1,0,-1，Rn+p(c) is the standard unit sphereSn+p(1)， Euclidean spaceEn+pand hyperbolic spaceHn+p(-1) respectively. Choose an orthonormal frame fields

{e1,…,en,en+1,…,en+p}

alongMsuch that {e1,…,en} are tangent toMand {en+1,…,en+p} are normal toM. Their dual frame fields are {θ1,…,θn} and {θn+1,…,θn+p} respectively. It is well known thatθn+1=…=θn+p=0 when they are restricted overM. Throughout this paper, we employ the Einstein summation convention, which states that repeated copies of the same index are summed over. Additionally, we adopt the following convention forthe range of the various indices:

1≤A,B,C,D，…≤n+p,1≤i,j,k,l，…≤n,n+1≤α,β,γ,δ，…≤n+p.

LetIIdenote the second fundamental form of the submanifoldφ:Mn→Nn+p， which can be expressed in terms of the frame fields and their duals as:

where ? denotes the tensor product andhαijdenotes the tensor components of the second fundamental form. Additionally define the following quantities:

In differential geometry, there is a famous classic Willmore functional for submanifold in unit sphereφ:Mn→Sn+p(1) which is defined as

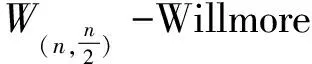
Due to the importance of Willmore conjecture, many geometric experts generalized the classic Willmore functional to a wide range and some interesting results have been obtained. For examples, Wu [12] considered theW(n,r)functional

for submanifold inSn+p(1) which simply measures how derivationsφ(M) from a totally umbilical submanifold

It is well known that the Simons’ integral inequality in [13] plays an important role in the study of minimal submanifold. It says that ifMis ann-dimensional compact minimal submanifold in (n+p)-dimensional unit sphereSn+p(1)， then

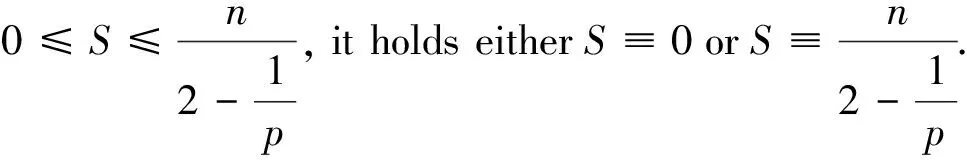
For functionalW(n,r)(φ)， Wu in [12] proved some Simons’ type integral results which say ifMis ann-dimensional compact critical points ofW(n,r)(φ) in unit sphereSn+p(1)， then

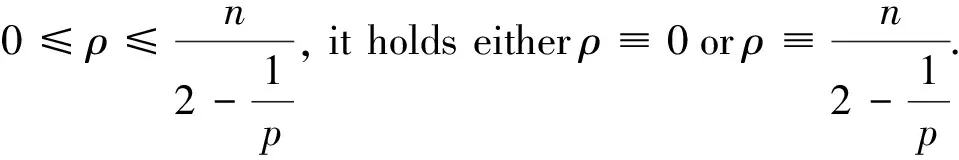
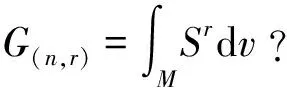
In this paper,we will give a positive confirmation to the above three questions. Concretely we focus the functional about square length of second fundamental form

FunctionalG(n,r)(φ) has a closed relation with Willmore Conjecture. In fact,obviouslyρ=S-nH2， thus whenMis minimal,ρ=S， andW(n,r)=G(n,r).

Above all, it is natural and meaningful to study the functionalG(n,r)(φ). In geometric meaning, the functional measures how derivationsφ(M) form a totally geodesic submanifold and generalize the well known classic Willmorefunctional. In this paper, we study the variational problem and gap phenomenon ofG(n,r)(φ).

The rest of this paper is organized as follows. In section 2, the structure equations of submaifolds and the variation formulas of the second fundamental form are established. In section 3, using the basic formulas in section 2, we calculate the first variation ofG(n,r)(φ). When the ambient manifoldNn+pis unit sphere,in section 4, according to the formulas in section 3, we construct some examples of critical points ofG(n,r)(φ). In section 5, using two famous matrix inequalities, we derive out some Simons’ type integral inequalities. Based on the foregoing results, a gap phenomenon has been classified in section 6.

2 Structure equations and basic variation formulas

Letφ:Mn→Nn+pbe ann-dimensional compact submanifold without boundary in an (n+p)-dimensional general ambient manifold, and Φ(·,·):Mn×(-ε,ε)→Nn+pbe a variation ofφ. This means that

φt=:Φ(·,t):Mn×{t}→Nn+p,?t∈(-ε,ε)

is an isometric immersion withφ0≡φ.

Lets=(s1,…,sn,sn+1,…,sn+p) andσ=(σ1,…,σn,σn+1,…,σn+p) be the orthonormal local frame fields of tangent vector bundleTNn+pand cotangent vector bundleT*Nn+p，respectively. Then,e=(e1,…,en,en+1,…,en+p)=φ-1tsis the set of orthonormal local frame fields of the pull-back vector bundleφ-1tTNn+poverMn×{t}. Note since

φ-1tTNn+p=TMnt⊕T⊥Mnt,

{e1,…,en} are tangent toMnand {en+1,…,en+p} are normal toMn.

Letωdenote the connection form overTNn+p. By the pull-back operation, we can assume the following decomposition:

Φ*σ=θ+Vdt,Φ*σA=θA+VAdt,
Φ*σi=θi+Vidt,Φ*σα=θα+Vαdt,
Φ*ω=φ+Ldt,Φ*ωBA=φBA+LBAdt,
Φ*ωji=φji+Ljidt,Φ*ωαi=φαi+Lαidt,
Φ*ωiα=φiα+Liαdt,Φ*ωβα=φβα+Lβαdt.

From submanifold theory or [15], it is well known that {θi} are the orthonormal frame fields ofT*Mn， {φji} is the connection form ofTMn， {φβα} is the connection form ofT⊥Mn，{φαi=hαijθj} is the second fundamental form, andθn+1≡…≡θn+p≡0 when they are restricted overMn.

One can also derive that {Vi,Vα} are the variation vector fields of Φ， meaning that

It must be mentioned that in variational theory, generally speaking, the tangential variation vector fields∑iVieihave little role in the calculations. So, we assume in this paper that only normal variation vector fields need to be considered

From the second fundamental form, we can construct some notations which are useful in the variation calculation. First, when the codimension of submanifoldφ:Mn→Nn+pis 1, it meansMnis a hypersurface, we can introduce

Second, when the codimension ofφ:Mn→Nn+pis greater than 1, we can introduce

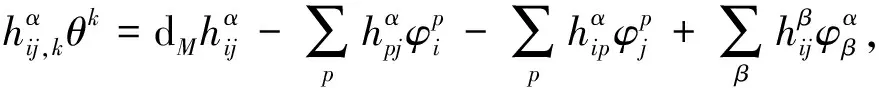
Let Ω， Ω┬, and Ω⊥denote the curvature forms ofTNn+p，TMn， andT⊥Mn， respectively. Hence their components and some other algebraic identities are as follows:

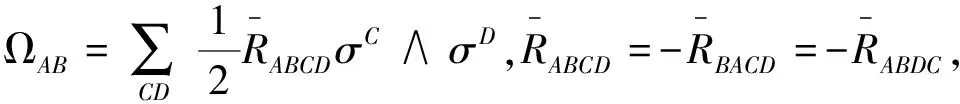
Φ*Ω=Ψ+dt∧P,Φ*ΩAB=ΨAB+dt∧PAB,

where Ψ denotes the pull back curvature form without dt， whilePdenotes 1-form with dt.

Following from the definitions:

Hence

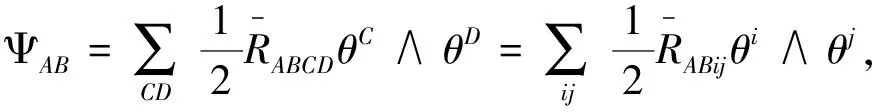
From any standard differential geometry text book or [15], one has the structure equations of Riemannian manifold

ω+ωT=0,dσ-σ∧ω=0,
Ω+ΩT=0,Ω=dω-ω∧ω,

whereωT, ΩTdenote the transpose ofω, Ω respectively. By pulling back the both sides of structure equations,one has

Φ*ω+Φ*ωT=0,

(1)

dM×(-ε,ε)Φ*σ-Φ*σ∧Φ*Ω=0,

(2)

Φ*Ω+Φ*ΩT=0,

(3)

Φ*Ω=dM×(-ε,ε)Φ*ω-Φ*ω∧Φ*ω.

(4)

Compare both sides of (1),(2),(3) and (4)， one has the following Lemmas.

Lemma 2.1([11,15,16]). Letφ:Mn→Nn+pbe a submanifold, and ∑αVαeαbe a normal variation vector field, one has

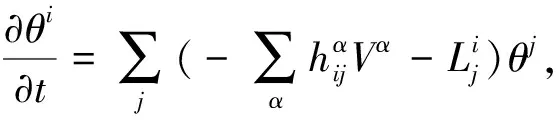
Lemma 2.2([11,15,16]). Letφ:Mn→Nn+pbe a submanifold, one has structure equations

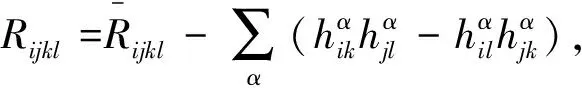
Lemma 2.3([11,15,16]). Letφ:Mn→Nn+pbe a submanifold, and ∑αVαeαbe a normal variation vector field, one has

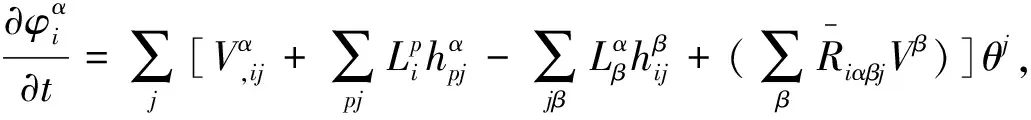
From any standard differential geometry text book or reference [15], one has the Ricci identity about tensor’s second derivatives.

Lemma 2.4([15]). Letφ:Mn→Nn+pbe a submanifold, andTl1…lq;α1…αrk1…kpbe a tensor over pullback vector bundleφ-1TN， one has

In particular, when the tensor in Lemma 2.4 is second fundamental formhαij， together with equations in Lemma 2.2, we have a special Ricci identity.

Lemma 2.5([11,15,16]). Letφ:Mn→Nn+pbe a submanifold, one has

ProofBy Lemma 2.4, we have

Substituting the equations in Lemma 2.2 in to the above formula, easily the desired result is obtained.

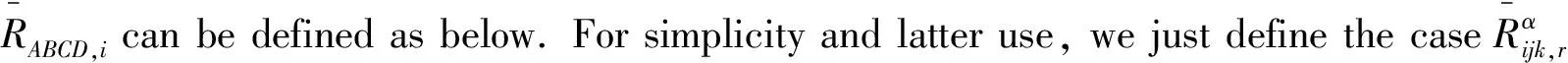
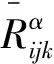
Lemma 2.6Letφ:Mn→Nn+pbe a submanifold, one has

Finally, one additional lemma is useful for our results.

Lemma 2.7([16]). With the same notations as above, one has

3 The first variation calculation

To calculate the first variation of functionalG(n,r)(φ)， two additional lemmas are needed.

Lemma 3.1Letφ:Mn→Nn+pbe a submanifold, and ∑αVαeαbe a normal variation vector field. Suppose dv=θ1∧…∧θndenotes the volume element, one has

which completes the proof.

Lemma 3.2Letφ:Mn→Nn+pbe a submanifold, and ∑αVαeαbe a normal variation vector field, one has

ProofBy Lemmas 2.3 and 2.7, one has

which completes the proof.

Use Lemmas 3.1 and 3.2 together, we can calculate the first variation formula of functionalG(n,r)(φ).

Theorem 3.1Letφ:Mn→Nn+pbe ann-dimensional submanifold in an (n+p)-dimensional general real ambient manifoldNn+p， thenMis a critical point ofG(n,r)(φ) if and only if for anyα∈[n+1,n+p]

(5)

When codimensionp=1， the above equation becomes

(6)

ProofUsing Lemma 3.1, Lemma 3.2, and Stoke’s theorem of integration by parts, we calculate

which completes the proof.

From any one standard differential geometry text book or [15], we know the curvature of space formsRn+p(c) are

Thus

Together with Theorem 3.1, we can derive out the following corollaries.

Corollary 3.1Letφ:Mn→Rn+p(c) be ann-dimensional submanifold in an (n+p)-dimensional space formsRn+p(c)， thenMis a critical point ofG(n,r)(φ) if and only if for anyα∈[n+1,n+p]

(7)

When codimensionp=1， the above equation becomes

(8)

Corollary 3.2Letφ:Mn→Rn+1(c) be an isoparametric(all principal curvatures are constant ) hypersurface in an (n+1)-dimensional space formsRn+1(c)， thenMis a critical point ofG(n,r)(φ) if and only if

(9)

For the use in examples construction, it is necessary to expand the first term of the equations in (5) when the ambient manifoldNn+pisRn+p(c).

Corollary 3.3Letφ:Mn→Rn+p(c) be ann-dimensional submanifold in an (n+p)-dimensional space formsRn+p(c)， thenMis a critical point ofG(n,r)(φ) if and only if for anyα∈[n+1,n+p],

(10)

ProofNotice that in space formsRn+p(c)， by Lemma 2.2, there holds the fact

hαij,k=hαik,j

which should be used repeat in the expanding of ∑ij(rSr-1hαij),ij.

+r(r-1)Sr-2S,ihαij,j+r(r-1)Sr-2S,jhαij,i+rSr-1hαij,ij]

Substituting the above expression into (5), the desired result is obtained.

4 Construction of examples

In this section, we use equations in Theorem 3.1 and its corollaries to explore critical points ofG(n,r)(φ) in unite sphere, the main technique is to solve algebraic equations.

Example 4.1Totally geodesic submanifolds in unit sphere are critical points ofG(n,r)(φ).

Example 4.2Letφ:Mn→Sn+1(1) is a totally umbilical but not totally geodesic hypersurface in unit sphere, according to the definition, suppose all principal curvatures are

k1=k2=…=kn=λ=constant>0.

Through a direct calculation, we obtain

H=λ,S=nλ2,P3=nλ3,

substituting them into the equation (9), we have an algebraic equation of critical points ofG(n,r)(φ)

which means that there exists a particular totally umbilical but not totally geodesic hypersurface in unit sphere satisfying the critical points ofG(n,r)(φ).

Example 4.3For a particular hypersurface withn≡0(mod2)

All principal curvatures are

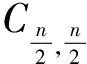
Example 4.4Torus withS=n. For a torus with parametersλ,μ,0<λ,μ<1,λ2+μ2=1.

Sm(λ)×Sn-m(μ)→Sn+1(1),1≤m≤n-1.

Obviously, all principal curvatures are

Then the quantityρis

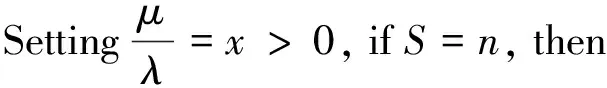
We solve the equation

Hence

and

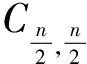
Example 4.5For a family hypersurfaces with parameterλ,μ,0<λ,μ<1,λ2+μ2=1,

Sm(λ)×Sn-m(μ)→Sn+1(1),1≤m≤n-1.

Obviously, all principal curvatures are

Then the quantitiesH,S,P3are respectively

m(2r-m)x6+m(n-m+2r)x4-(n-m)(m+2r)x2+(n-m)(n-m-2r)=0.

Settingy=x2， then the above equation becomes

g(y)=:m(2r-m)y3+m(n-m+2r)y2-(n-m)(m+2r)y+(n-m)(n-m-2r)=0.

In fact, the equation ofg(y) essentially are 3 order polynomial, which can be solved completely, but depends on the parametersn,r,m.

Example 4.6Let (x,y,z) be a natural coordinates ofR3and (u1,u2,u3,u4,u5) be the natural coordinate system ofR5， we consider the mapping as below

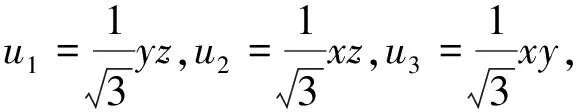
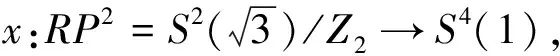
Then we calculate

H3=H4=0,S333=S344=S433=S444=0.

Substituting them into the equation (7), one can conclude that Veronese surface always is a critical point ofG(n,r)(φ).

Example 4.7Letφ:Mn→Sn+p(1),n≥3 be a minimal submanifold in unit sphere. Ifφ:Mn→Sn+p(1) is also Einstein, then it must be a critical point ofG(n,r)(φ).

ProofSinceMis minimal and Einstein, according to the definitions, one has

It is well known that whenn≥3

R=constant.

By Lemma 2.2, one has

Obviously

S=n(n-1)-R=constant.

According to the condition of Einstein, one has

Wheni=j， one has

Wheni≠j， one has

Thus for any indexn+1≤α≤n+p， one has

All above substituting into equation of Corollary 3.3, we conclude that a minimal and Einstein submanifold in unit sphere must be a critical point ofG(n,r)(φ).

Example 4.8([17]). Let

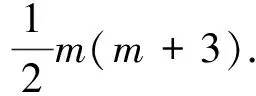
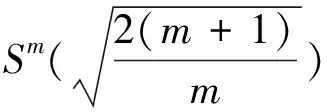
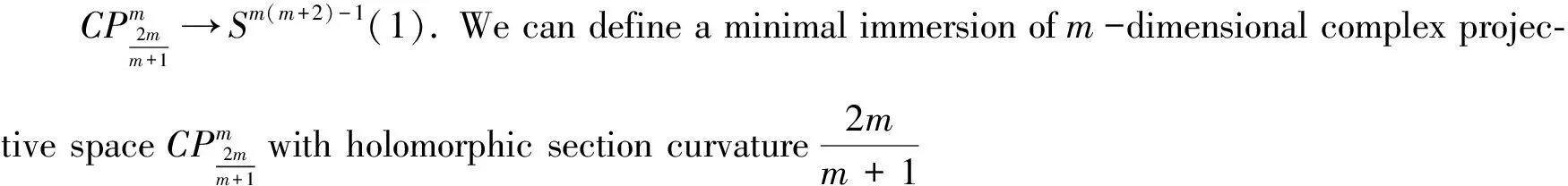
5 Simons’ type integral inequalities

Some lemmas are needed for the establishment of Simons’ type integral inequalities. We start with some basic facts on matrices. For an (n×n) matrixA， we define its square length

The following properties are obvious:N(A)≥0 for any matrixA， andN(A)=0 if and only ifA≡0;N(A)=N(TATt)=N(TA) for any orthogonal matrixTand for any matrixA;N(AB-BA)=2tr(AABB-ABAB) for any two symmetric matricesA,B.

Lemma 5.1([14]). IfAandBare symmetric matrices, then

N(AB-BA)≤2N(A)N(B),

and the equality holds if and only if eitherA，Bor one of them must be zero, orAandBcan be transformed simultaneously by an orthogonal matrix into multiples of the following matrixes respectively:

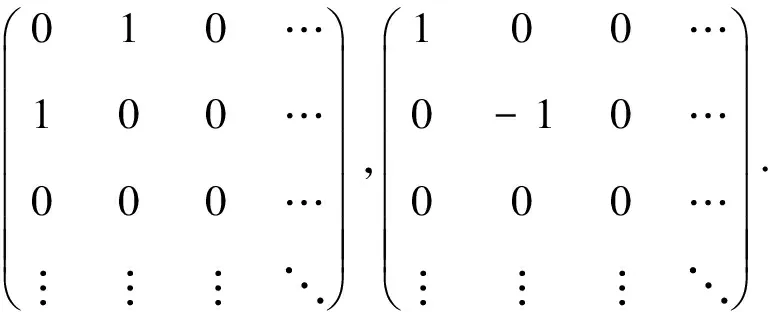
Moreover, ifB1,B2,B3are (n×n)-symmetric matrices satisfying

N(BiBj-BjBi)=2N(Bi).N(Bj),1≤i,j≤3,

then at least one of the matricesBimust be zero.

Lemma 5.2Letφ:Mn→Nn+pbe a submanifold withp≥2，S,Sαβ,Aαas defined in section 2, one has estimate

ProofDiagonalize (Sαβ) such thatSαβ=0,α≠β， by Lemma 5.1 and Cauchy-Schwartz inequality, one has

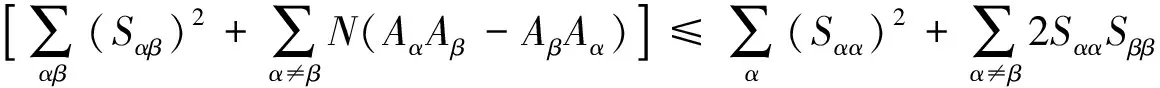
Lemma 5.3([18]). LetB1,…,Bp,p≥2 be symmetric (n×n) matrices.Setting

One has

and ≤ becomes = if and only ifB1,…,Bp,p≥2 satisfy one of the below two conditions

(1)B1=B2=…=Bp=0;

(2)B1≠0,B2≠0,B3=B4=…Bp=0,L11=L22.

When condition (2) holds,B1,B2can be transformed simultaneously by an common orthogonal matrix into the following matrices respectively:

Lemma 5.4Letφ:Mn→Nn+pbe a submanifold withp≥2，S,Sαβ,Aαas defined in section 2, one has estimate

ProofLemma 5.4 is a directly consequence of Lemma 5.3.

Lemma 5.5Letφ:Mn→Nn+pbe a submanifold.

(i) When codimensionp=1， one has

(ii) When codimensionp≥2， one has

(iii) When codimensionp≥2， one has

(iv) When codimensionp≥2， one has

ProofBy the definition ofSand Laplacian operator, one has

(11)

We denote the last term ∑ijkαhαijhαij,kk=:T1， by Lemma 2.2, one obtains

(12)

Furthermore, we denote the last term ∑ijkαhαij(hαik,jk-hαik,kj)=:T2， by Lemma 2.5, one has

According to the definition of trace andN(·)，one has

(13)

Substituting (13) into (12), one has

(14)

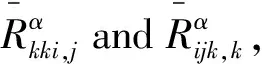
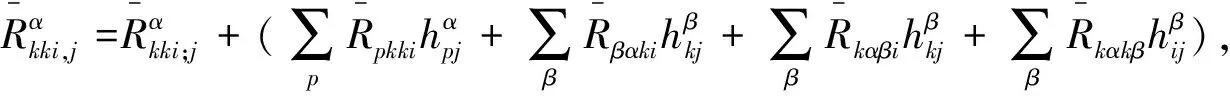
Together with Bianchi identities and changing the index, one has

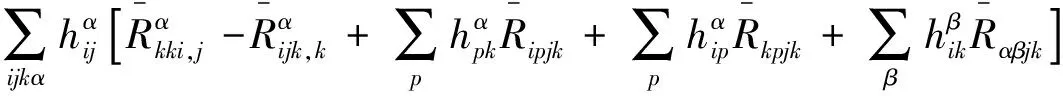
(15)

Putting (15) into (14), one has

(16)

When codimensionp=1， one has

(17)

When codimensionp≥2， by Lemma 5.2, one has

(18)

When codimensionp≥2， by Lemma 5.4, one has

(19)

Putting (16),(17),(18),and (19) into (11), the desired results are obtained.

Lemma 5.6Letφ:Mn→Nn+pbe a submanifold,Sdefined as before andr≥1， one has

Δ(Sr)=r(r-1)Sr-2|S|2+rSr-1Δ(S).

(i) When codimensionp=1， one has

Δ(Sr)=r(r-1)Sr-2|

+2rSr-1|

(ii) When codimensionp≥2， one has

(iii) When codimensionp≥2， one has

Δ(Sr)≥r(r-1)Sr-2|

+2rSr-1|

(iv) When codimensionp≥2， one has

Δ(Sr)≥r(r-1)Sr-2|

+2rSr-1|

ProofBy the definition of Lapalacian operator, one has

together with Lemma 5.5, the desired results are obtained.

Integrating both sides of equalities and inequalities in Lemma 5.6, together using the Stokes’ theorem and equations in Theorem 3.1, we can derive out the following theorem.

Theorem 5.1Letφ:Mn→Nn+pbe a critial submanifold ofG(n,r)(φ) withr≥1.

(i) When codimensionp=1， one has

(ii) When codimensionp≥2， one has

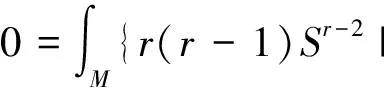
(iii) When codimensionp≥2， one has

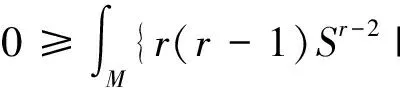
(iv) When codimensionp≥2， one has

ProofSinceφ:Mn→Nn+pis a critical point ofG(n,r)(φ)， one has

Integrating the second term in Lemma 5.6, by Stokes’ theorem

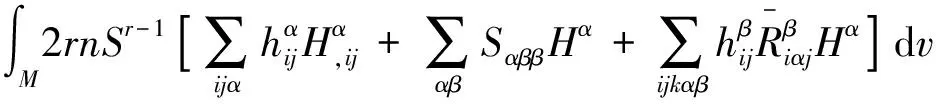
Thus, we can easily derive out the integral equalities and inequalities in Theorem 5.1.

From any standard differential geometry text book or [15], we know the curvature of space formsRn+p(c) are

Together with Theorem 5.1, we can derive out the following corollary.

Corollary 5.1Letφ:Mn→Rn+p(c) be a critial submanifold ofG(n,r)(φ) in space form withr≥1.

(i) When codimensionp=1， one has

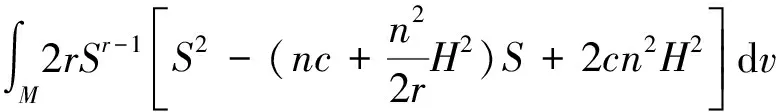
(ii) When codimensionp≥2， one has

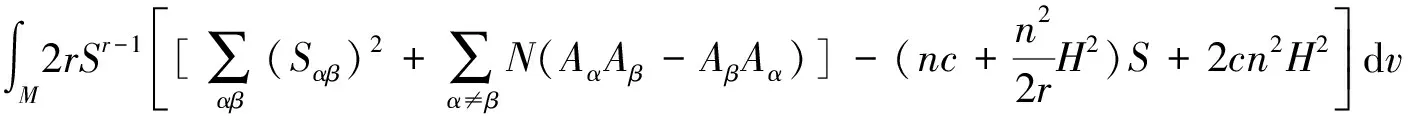
(iii) When codimensionp≥2， one has

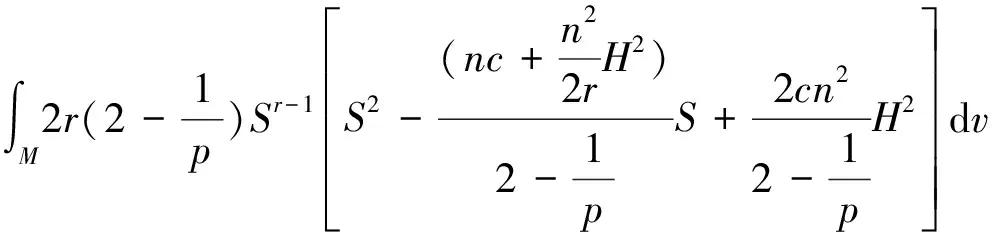
(iv) When codimensionp≥2， one has

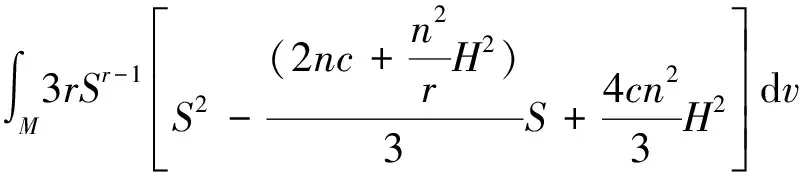
6 Gap phenomenon of critical points

In order to give a classification of the boundary points of the Simons’ type integral equalities or inequalities, we need three very important conclusions which are treated as a Lemma and a main Theorem in [14] and a theorem in [18]. For a hypersurface, we choose frame fields in such a way thathij=0,?i≠j,hi=hii.

Lemma 6.1([14]). Letφ:Mn→Sn+1(1) be a compact hypersurface withh≡0， then there are two cases.(1).h1=…=hn=λ=constant， andMis a totally umbilic(λ>0) or totally geodesic (λ=0);(2).andMis a Riemannian product ofM1×M2， where

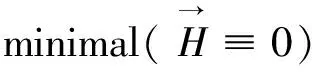
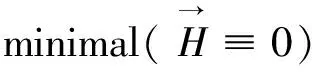
Based on examples in section 4 and Lemmas in section 5 and section 6, we can derive out the following theorems, which draw a picture of the gap phenomenon of critical points ofG(n,r)(φ).

ProofSinceMis minimal,i.e.,H2=0， by the (i) of Corollary 5.1, one has

If 0≤S≤n， we have 2rSr(S-n)≤0 and

Since

we have

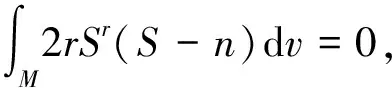
Thus we obtainS≡0 orS≡nandh=0.

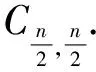
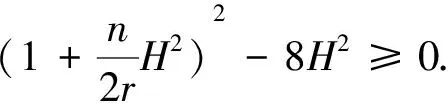
then

or

For the former case,Mis a torusSm(λ)×Sn-m(μ)→Sn+1(1),1≤m≤n-1, determined by

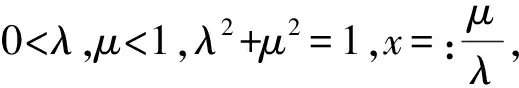
For the latter case,Mis a torusSm(λ)×Sn-m(μ)→Sn+1(1),1≤m≤n-1, determined by

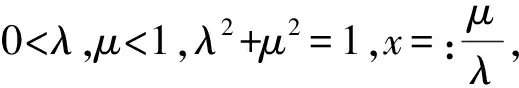
ProofWe denote

and

By (i) of Corollary 5.1, we have

Ifa≤S≤b， we have 2rSr-1(S-a)(s-b)≤0 and

Since

we have

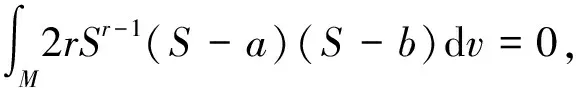
Thus we obtainS≡aorS≡bandh=0. WhenS=a,b， by Lemma 6.1 and Example 4.5, we can conclude thatMis a torus determined through algebraic equations.

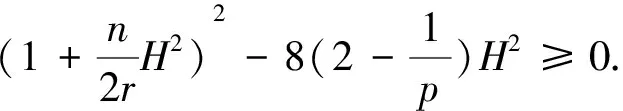
and

ProofWe denote

and

By (iii) of Corollary 5.1, one has

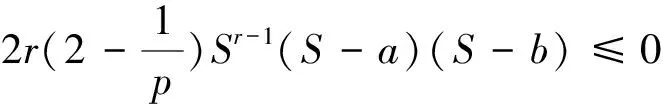
Since

we have

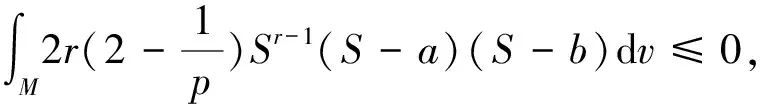
Thus we obtainS≡aorS≡bandh=0. By Lemma 5.1 and the proof process of Lemma 5.5, we have some inequalities in Lemma 5.5 must be equalities. ThusH2=0， by Lemma 6.2 and Example 4.6, we can conclude that (i)a=0 andMis totally geodesic;(ii)andMis Veronese surface inS4.

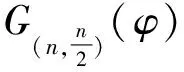
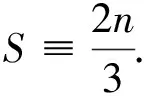
ProofWe denote

and

By the (iii) of Corollary 5.1, one has

Ifa≤S≤b， we have 3rSr-1(S-a)(S-b)≤0 and

Since

we have

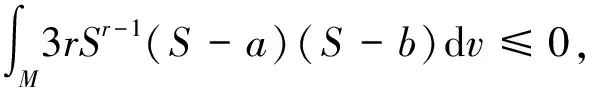
Thus we obtainS≡aorS≡bandh=0. By Lemma 5.3 and the proof process of Lemma 5.5, some inequalities in Lemma 5.5 must be equalities. ThusH2=0， by Lemma 6.3 and Example 4.6, we can conclude that (i)a=0 andMis totally geodesic;(ii)andMis Veronese surface inS4.

7 Conclusion

In this paper, one power type functional concerning the square length of second fundamental form has been constructed which generalizes the well known classic Willmore functional, we calculate the first variational equation. Using some algebraic technique, some examples of critical points ofG(n,r)functional are constructed or proven. Based on the first variational calculation, the higher derivative computation of functionSr， and some trickly inequalities, we have established some Simons’ type integral inequalities forG(n,r)submanifolds. Without any surprise, isoparametric torus inSn+1(1) and Veronese surface inS4(1) still play an important role in the discussion of gap phenomenon and show us an interesting picture aboutG(n,r)submanifolds.