具有二次自作用的捕食-食餌系統的動力學分析

(昆明理工大學津橋學院理工學院,昆明,650106)

1 引言

近年來，很多學者研究了隨機生物模型[1-4]. 本文考慮下面的捕食-食餌模型：

dx(t)=x(t)[a1-b1x(t)-c1y(t)]dt+α1x(t)dB1(t),
dy(t)=y(t)[-a2+b2x(t)+c2z(t)]dt+α2y(t)dB2(t),
dz(t)=z(t)[a3-b3y(t)-c3z(t)]dt+α3z(t)dB3(t),

(1.1)

其中x(t)，z(t)分別表示食餌A和食餌B種群在時刻t的種群密度，y(t)表示捕食者種群在時刻t的種群密度.a1，a3分別表示沒有捕食者的情況下食餌A和食餌B種群的增長率，a2表示沒有食餌的情況下捕食者種群的死亡率.c1，b3分別表示由于捕食造成的食餌A和食餌B種群的死亡率.b2，c2分別表示捕食者種群對食餌A和食餌B的消耗率.b1，c3分別表示食餌A和食餌B種群的二次自作用率.Bi(t)(i=1,2,3)表示一維的標準布朗運動，α2i(i=1,2,3)表示各種群受到的白噪聲的強度.假設文中所涉及的所有參數及變量均為正的.

2 預備知識

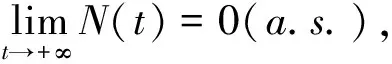
定義2[5]N(t)被稱為是均值意義下持久的，若[N]*>0(a.s.).

引理1[6]對任意給定的初始值(x(0),y(0),z(0))T∈R3+，系統(1.1)當t≥0時，存在唯一一個正解，且這個解將以概率1存在于R3+中. 再者，解(x(t),y(t),z(t))T∈R3+滿足

引理2[6](1)若存在T>0，λ0>0使得

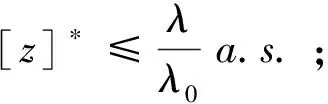
(2)若存在T>0，λ>0，λ0>0使得

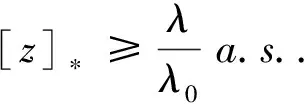
3 主要結論

在研究種群動力學時我們總關心物種是否持續發展或滅絕.

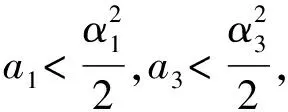
證明對系統(1.1)應用伊藤公式得

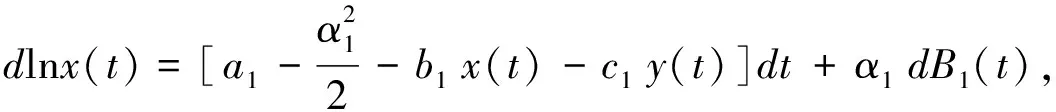
上述等式兩端同時從0到t積分并除以t，得

(3.1)

(3.2)

(3.3)

由(3.1)和(3.3)分別有

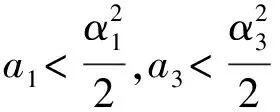
由(3.2)有

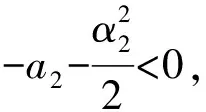
定理證畢.

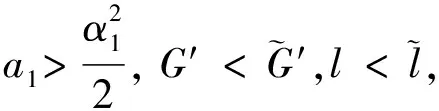
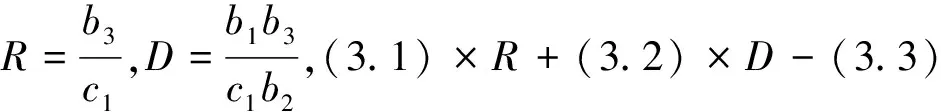
由引理3.1，當t充分大時有

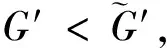
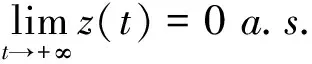
(3.4)

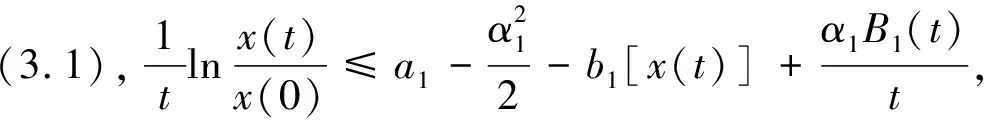
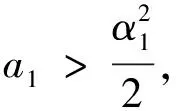
(3.5)

(3.1)式乘以b2再加上(3.2)式乘以b1，有

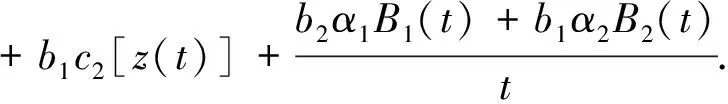
由引理3.1及(3.4)，當t充分大時有

由引理3.2(1)有

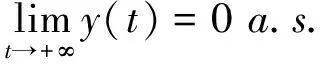
結合(3.4)，由(3.1)得

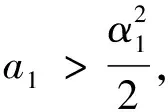
定理證畢.