New Inequalities for the Hadamard Product of Nonsingular M-matrices

Chen Fubin

(Science Department，Oxbridge College，Kunming University of Science and Technology，Kunming 650106，China)

Abstract Some new inequalities for the minimum eigenvalue of nonsingular M-matrices are given. A numerical example is given to show that the new inequalities are better than some existing ones.

Key words M-matrix Hadamard product Lower bound Minimum eigenvalue

1 Introduction

The set of all real (complex) matrices is denoted byRn×n(Cn×n).Ndenotes the set {1,2,…,n} throughout.

If ann×nmatrixAsatisfiesA=λI-Bandλ≥ρ(B), whereBis a nonnegative matrix,λis a nonnegative real number andρ(B) is the spectral radius of matrixB,Iis an identity matrix, thenAis called anM-matrix. Furthermore, ifλ>ρ(B), thenAis called a nonsingularM-matrix, and is denoted asA∈Mn[1]; ifλ=ρ(B), thenAis called a singularM-matrix.

Our work is based on the following simple facts (see Problems 16,19 and 28 in Section 2.5 of [2] ):

(1)τ(A)∈σ(A),τ(A)= min {Re(λ):λ∈σ(A)} denotes the minimum eigenvalue ofA.

(2)τ(A)≥τ(B), whenA,B∈MnandA≥B.

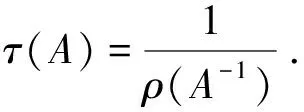
The Hadamard productA°BofAandBis defined asA°B=(aijbij). IfA,B∈Mn, thenB°A-1∈Mn[3].

A matrixAis irreducible if there does not exist any permutation matrixPsuch that

whereA11,A22are square matrices.

Given a matrixA=(aij)∈Rn×n, for anyi∈N, let

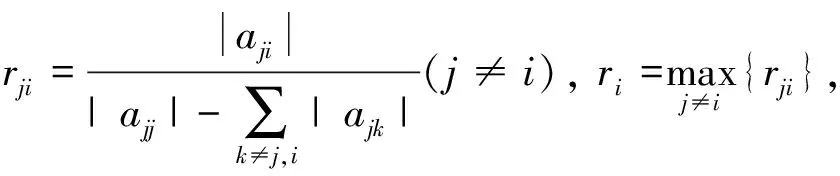
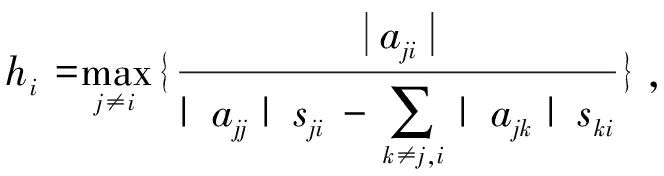
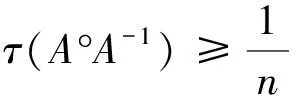
In [9], Li et al. gave the following result

Furthermore, ifa11=a22=…=ann, they have obtained

In [10], Li et al. gave the following sharper result

In this paper, our motives are to improve the lower bounds for the minimum eigenvalue ofM-matrices, which improve some existing results.

2 Main results

In this section, we give some lemmas that involve inequalities for the entries ofA-1. They will be useful in the following proofs.

Lemma 2.1[13]LetA,B∈Cn×nand suppose thatE,F∈Cn×nare diagonal matrices. Then

E(A°B)F=(EAF)°B=(EA)°(BF)=(AF)°(EB)=A°(EBF).

Lemma 2.2[14]LetA∈Mn, andD=diag(d1,d2,…,dn),(di>0,i=1,2,…,n). ThenD-1ADis a strictly row diagonally dominantM-matrix.

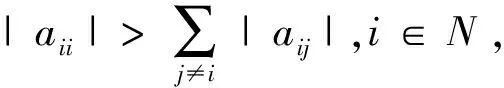
Lemma 2.4[15]IfA=(aij)∈Cn×n, then there existx1,x2,…,xn(xi>0) such that

Lemma 2.5[16]IfA-1is a doubly stochastic matrix, thenAe=e,ATe=e, wheree=(1,1,…,1)T.

Lemma 2.6[3]IfP∈Mnis irreducible, andPz≥kzfor a nonnegative nonzero vectorz, thenτ(P)≥k.

Theorem 2.1IfA=(aij)∈Mnwith strictly row diagonally dominant, thenA-1=(βij) satisfies

ProofThe proof is similar to the Theorem 2.1 in [9].

Theorem 2.2IfA=(aij)∈Mmwith strictly row diagonally dominant, thenA-1=(βij) satisfies

ProofLetB=A-1. SinceAis anM-matrix, soB≥0. ByAB=In, we have

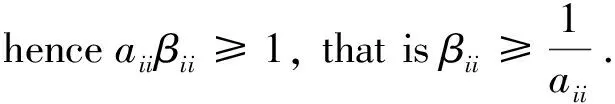
By Theorem 2.1, we have

i.e.,

Theorem 2.3LetA=(aij)∈Rn×nbe anM-matrix, and suppose thatA-1=(βij) is a doubly stochastic matrix. Then

ProofSinceA-1is a doubly stochastic andAis anM-matrix, we know thatAis strictly diagonally dominant by row. By Lemma 2.5, we have

and

Then, by Theorem 2.1, fori∈N

i.e.,

Theorem 2.4IfA=(aij),B=(bij)∈Mn, then

ProofBy Lemma 2.1, and Lemma 2.2, for convenience and without loss of generality, we assume thatAis a strictly diagonally dominant matrix by row.

First, we assume thatA,Bare irreducible. Letτ(B°A-1)=λandA-1=(βij), by Lemma 2.4 and Theorem 2.1, there exists anisuch that

i.e.,

By Theorem 2.2, we obtain

When one ofAandBis reducible.T=(tij) denotes the permutation matrix witht12=t23=…=tn-1,n=tn1=1, the remainingtijzero. We know thatA-εTandB-εTare irreducible nonsingularM-matrices withε>0[1]. we substituteA-εTandB-εTforAandB, the result also holds.

Corollary 2.1IfA=(aij),B=(bij)∈MnandA-1is a doubly stochastic matrix, then

Corollary 2.2IfA=(aij)∈MnandA-1is a doubly stochastic matrix, then

Theorem 2.5IfA=(aij)∈Mnis irreducible strictly row diagonally dominant, then

ProofSinceAis irreducible, thenA-1=(βij)>0, andA°A-1is again irreducible. Note that

τ(A°A-1)=τ((A°A-1)T)=τ(AT°(AT)-1).

Let

(AT°(AT)-1)e=(d1,d2,…,dn)T,

wheree=(1,1,…,1)T. Without loss of generality, we assume thatd1=mini{di}, by Theorem 2.1, we have

Therefore, by Lemma 2.6, we have

RemarkSinceA∈Mnis a strictly row diagonally dominant，so 0≤sji≤dj<1 , then

By the definition ofhi, we have

hence

By 0≤hi≤1, we havevji≤sjiandvi≤si.

Therefore, it is easy to obtain that

That is to say, the bound of Corollary 2.2 is sharper than Theorem 3.1 and the bound of Theorem 2.5 is sharper than Theorem of 3.5 in [9].

3 An example

Let

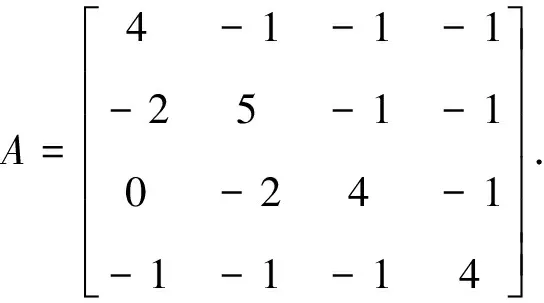
By Theorem 3.1 of [9], we have

By Theorem 3.2 of [10], we have

If we apply Corollary 2, we have