航空發動機作動筒的伺服控制建模與分析
吳吉麟,張 金,金林山,李明磊
(中國航發控制系統研究所,江蘇無錫214063)
0 引言
自20世紀50~60年代開始,基于經典控制理論以反饋控制為主體的電液伺服控制技術逐漸發展為綜合電氣技術、液壓技術與控制領域的自動化技術[1-6]。電液伺服控制系統以其體積小、功重比輸出高、響應速度快、低速平穩性好、調速范圍寬及自潤滑等特點,在軍事、航空航天以及民用工程等自動化控制領域占據著非常重要的位置,其應用也越來越廣。航空發動機作動筒的控制就是電液位置伺服控制系統的典型應用。
在電液位置伺服控制系統中,作動筒屬于執行元件,用于將液壓能轉換為驅動發動機導葉、活門或其他機械裝置的機械能。在當前電液位置伺服控制研究中,多采用對稱作動筒設計和分析討論[7-12]。而在航空領域,因非對稱作動筒具有結構簡單、加工方便、工作空間小、單邊活動密封效率及可靠性高等特點而被廣泛應用。但是由于非對稱作動筒結構參數的不對稱,導致閥控作動筒在伸出和縮回2個方向上動態特性(如超調量、調節時間和穩態誤差等)不對稱,并且在活塞換向時存在壓力突變,影響整個液壓系統的平穩性。這種本質上的非線性給系統控制帶來困難。當前有不少通過應用非對稱閥控制非對稱作動筒或者智能算法(如模糊控制、自適應控制等)來實現對稱控制[13-15],能在一定程度上解決控制的非對稱性問題,但往往忽略了負載對伺服控制的影響,而且在航空發動機電液位置伺服控制實際應用時,考慮到實際生產效益、可靠性問題,很少用到非對稱閥控制非對稱作動筒(以下簡稱作動筒)以及復雜控制算法的場合。隨著航空發動機對實際帶負載工況下作動筒位置控制的動態特性和控制精度要求的提高,有必要對帶負載工況下閥控非對稱作動筒位置伺服控制系統的工程應用作進一步深入研究。
因此,本文針對帶負載工況下典型航空發動機電液伺服閥控制作動筒的伺服控制系統,基于對帶載下電液位置伺服控制系統的認識,在具體分析帶載閥控不對稱作動筒的基礎上進行分析與建模,并通過工程試驗進行檢驗,為電液位置伺服控制系統的設計和分析提供指導。
1 電液位置伺服控制系統的建模與設計
典型航空發動機閥控不對稱作動筒的電液位置伺服控制系統原理如圖1所示。其中PID控制模塊、D/A模塊、電流驅動電路、位置傳感器解調電路、A/D模塊都屬于電子控制器部分,電液控制模塊和作動筒為液壓控制部分,電液控制模塊通常采用電液伺服閥。作動筒位置信號通過位置傳感器采集反饋。

圖1 閥控不對稱作動筒電液位置伺服控制系統原理
1.1 閥控不對稱作動筒的分析
閥控不對稱作動筒部分為電液位置伺服控制系統的液壓動力執行機構,是伺服控制系統中的重要環節。電液伺服閥有雙噴檔電液伺服閥、射流管閥和射流偏轉板閥3種常見形式,無論哪種電液伺服閥,一般都會采用前置級加功率級的2級電液伺服閥結構形式。上述3種閥的主要區別在于前置級,而功率級都是采用滑閥的形式,且又是電液伺服閥的液壓輸出級,因此,典型閥控作動筒的結構通常可以簡化為滑閥控制作動筒的形式。典型航空發動機閥控作動筒的結構如圖2所示。
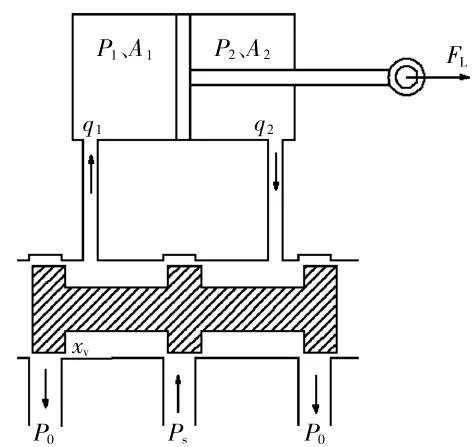
圖2 典型航空發動機閥控作動筒結構
常用電液伺服閥的滑閥可以看作零開口4邊滑閥,其4個窗口是匹配和對稱的。假設作動筒負載力為常量,供油壓力和低壓回油壓力為恒值。忽略管道中的壓力損失、管道動態特性、流體的壓縮性和泄漏、作動筒的慣性負載力、黏性負載力、彈性負載力和摩擦等非線性因素,建立作動筒流體連續性方程、作動筒與負載的力平衡方程、閥的流量方程
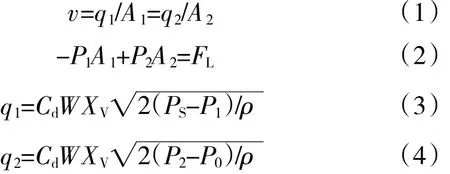
式中:v為作動筒活塞移動速度;q1、A1、P1分別為作動筒無桿腔的流量、油液有效作用面積和壓力;q2、A2、P2分別為作動筒有桿腔的流量、油液有效作用面積和壓力;FL為作動筒負載力(圖示方向為正方向);Cd為流量系數;W為閥口面積梯度;Xv為滑閥位移;Ps和P0為供油壓力和回油壓力;ρ為油液密度。供油壓力、回油壓力和作動筒負載力均由發動機狀態決定,設計作動筒時必須保證伸出或縮回時的液壓驅動力均大于負載力,否則可能出現電液伺服閥驅動不了作動筒的情況。
根據式(1)~(4)得到作動筒移動速度為

由此可得,閥控作動筒的速度增益為

由于 A1、A2、Ps、P0、FL、W 均為恒值,忽略流量系數和油液密度的變化,Kv0可看作1個常量。
對作動筒速度積分,得到作動筒位移為

對式(7)進行拉式變換,得到閥控作動筒的傳遞函數為

上面討論了作動筒在正向負載時作動筒活塞桿伸出運動的情況,同理也可得到作動筒在正向負載時作動筒活塞桿縮回運動時的速度增益
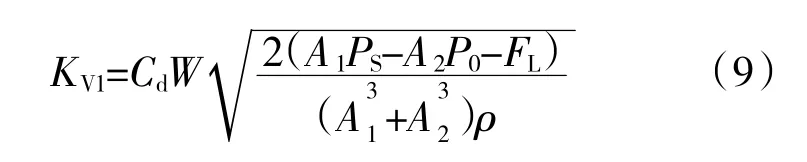
作動筒在反向負載時作動筒活塞桿伸出運動時的速度增益為

作動筒在反向負載時作動筒活塞桿縮回運動時的速度增益為
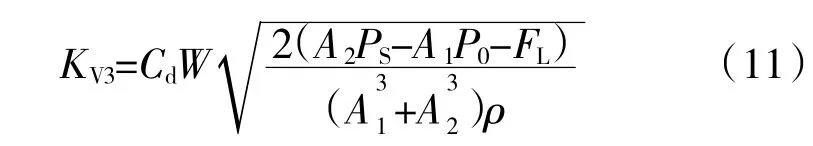
通過對比可知,負載方向為正向時,閥控作動筒縮回增益肯定小于伸出增益,不利于動態控制;當負載方向為反向時,閥控作動筒的縮回增益和伸出增益與負載力大小相關,當負載力滿足條件
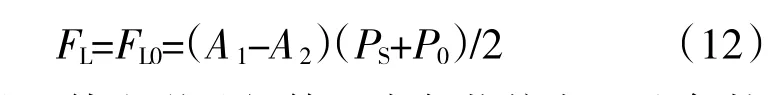
時,縮回增益和伸出增益相等。當負載偏離上述條件越大,縮回增益與伸出增益差值越大,且負載小于FL0時,伸出增益大于縮回增益;負載大于FL0時,伸出增益小于縮回增益。
因此,在作動筒負載設計時應盡量考慮反向,即使在作動筒活塞桿縮回的運動方向。同時,負載和作動筒2腔面積、供油壓力、回油壓力之間應盡量滿足作動筒往返運動的增益條件。
通常實際使用時控制器增益Kp是不變的,當作動筒伸出增益和縮回增益不一致時,表現出來就是位置伺服系統總增益不一致。當總增益較大時,系統的快速性好,但可能導致控制不穩定;當總增益較小時,系統的穩定性較好,但會犧牲一定的快速性。一般設計時以對應伸出增益和縮回增益中最大的增益進行,在這種狀態下設計的控制器增益最小,系統總增益最小,對應位置伺服系統控制的穩定性最好。
1.2 電液伺服閥的分析
電液伺服閥通常由力矩馬達、液壓放大器、反饋機構3部分組成。力矩馬達用于將輸入的電氣信號轉換為力矩或力,控制液壓放大器運動。液壓放大器的功率級閥體即為閥控作動筒結構中控制作動筒的滑閥。反饋機構可以將滑閥位移反饋到輸入端,使伺服閥對滑閥位移Xv構成1個閉環控制,有利于提高伺服閥的控制性能。
以電液伺服閥輸入電流i為輸入變量,以電液伺服閥功率放大級滑閥位移Xv為輸出變量,探討電液伺服閥的傳遞函數。在航空電液位置伺服控制系統中,雖然電液伺服閥由于磁滯、滑閥摩擦、沿程損失等原因存在一定的非線性,但是電液伺服閥的動態響應要高于動力元件的動態響應,其傳遞函數一般可以用2階振蕩環節表示[7]。因此,電液伺服閥的傳遞函數可以表示為
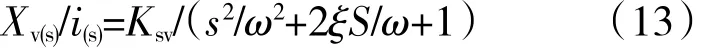
式中:w為電液伺服閥固有頻率;ξ為電液伺服閥阻尼比;Ksv為電液伺服閥增益。
因此,可以得到位置伺服系統中液壓控制部分的傳遞函數

式中:Ksv與電液伺服閥力矩馬達的中位電磁力矩系數、反饋桿剛度、反饋桿長度、噴嘴中心與彈簧管回轉中心距離有關[7];Kv為閥控作動筒速度增益Kv0、Kv1、Kv2、Kv3中的最大值,與電液伺服閥滑閥的面積梯度有關。而實際應用時,這些參數對于使用者而言都是未知的。因此,引入電液伺服閥規格參數對傳遞函數G1(s)進行修正。
電液伺服閥規格參數包括額定壓力Pn、線性工作最大流量 qmax、線性最大工作電流 imax。其中,qmax、imax為對應電液伺服閥流量特性曲線中零位附近線性度較好的最大工作流量和電流。由于在實際工作時,電液伺服閥電流大部分時間都是在零位附近,故這樣處理是有意義的。根據流量方程有

式中:Xmax為對應線性工作最大電流的閥芯位移。
結合閥控作動筒的方程,得到液壓控制增益和傳遞函數

通常qmax、imax可以默認為額定流量qn和額定電流In。考慮到有些電液伺服閥并不能做到全行程范圍內線性度很好,因此仍以qmax和imax來計算。
1.3 位置傳感器模塊的分析
位置傳感器的頻寬至少應是系統頻寬的3~10倍,否則無法借助傳感器測出被控物理量的瞬時真值,也會導致系統的階數過高,不便于綜合。通常情況下位置傳感器的頻寬一般都很大,因此位置傳感器常簡化為1個比例環節。
1.4 電子控制模塊的分析
電子控制模塊設計包括位置傳感器解調電路、A/D模塊、PID控制模塊、D/A模塊及電流驅動電路等部分。通常PID控制模塊為控制器軟件設計,其余為硬件電路設計。
位置傳感器解調電路和電流驅動電路頻寬要大于系統固有頻率,因此常簡化為1階慣性環節。A/D模塊和D/A模塊的轉換速率通常在kHz以上,遠大于系統固有頻率,一般可當作比例環節處理,但是其轉換精度在一定程度上影響信號處理的精度。
PID控制器(比例-積分-微分控制器)結構簡單,使用時也不需要精確的系統模型,在工業控制中應用最為廣泛。電液位置伺服系統中控制算法就采用經典PID控制。
1.5 電液位置伺服控制系統建模與設計
基于上述分析,同時綜合考慮軟件濾波、電液伺服閥零偏等非線性特征,應用Simulink軟件進行伺服控制系統建模,如圖3所示。

圖3 電液位置伺服控制系統PID仿真
基于上述模型,結合系統設計時的時域要求或頻域要求,得到1組比較理想的PID控制參數,其中的比例系數Kp即為系統控制器增益。
2 試驗驗證
以某型發動機壓氣機進口導葉作動筒的控制為案例,其伺服控制系統模型如圖4所示。

圖4 某型項目導葉伺服控制系統模型
根據模型,可以得到在施加反向負載800 N、供油壓力5.0 MPa、回油壓力0.2 MPa時,不同控制器增益Kp下的頻響指標,見表1。

表1 帶載時不同控制器增益Kp的階躍響應仿真指標
根據工程設計要求,通常系統設計時幅頻裕度為6 dB,相頻裕度為45°。因此,在Kp=3.0時,系統可能不穩定。而Kp=2.0時,系統可能處于臨界穩定狀態。
在該型發動機半物理試驗臺上,對進口導葉作動筒施加反向負載800 N,在導葉閉環穩定控制在某一位置的基礎上,通過模擬控制器給出1個10%全程階躍位置伸出的指令信號,測試其對應的階躍響應特性。在不同供油壓力下,對應Kp=2.0、3.0時的階躍響應試驗測試數據如圖5、6所示。從圖中可見,在Kp=3.0,供油壓力為5 MPa時,系統控制不穩,與仿真結論一致。

圖5 在Kp=2.0、不同供油壓力下10%階躍響應

圖6 在Kp=3.0、不同供油壓力下10%階躍響應
以施加反向負載800 N、供油壓力為5 MPa、Kp=2時,伺服控制系統20%階躍響應時仿真分析曲線與試驗測試曲線進行對比,結果如圖7所示。從圖中可見,仿真結果與試驗測試結果的上升時間一樣;仿真和試驗超調量誤差為30%;仿真和試驗調整時間誤差為25%。模型仿真分析具備較高的可信度。
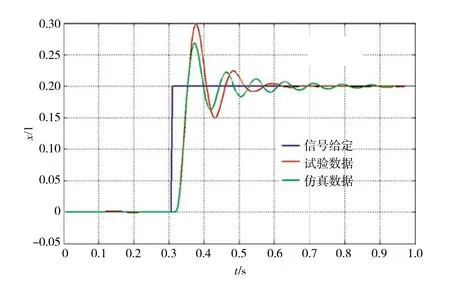
圖7 在20%階躍時的仿真與試驗結果對比
為了觀察負載對系統的影響,在供油壓力為5 MPa、Kp=2的條件下,分別對導葉伺服控制系統施加正向800 N負載和反向800 N負載 (通過分析計算可以得到對應狀態下FL0=400 N),統計作動筒伸出20%階躍和縮回20%階躍的動態響應試驗數據,結果見表2。表中調整時間以2%誤差來衡量。
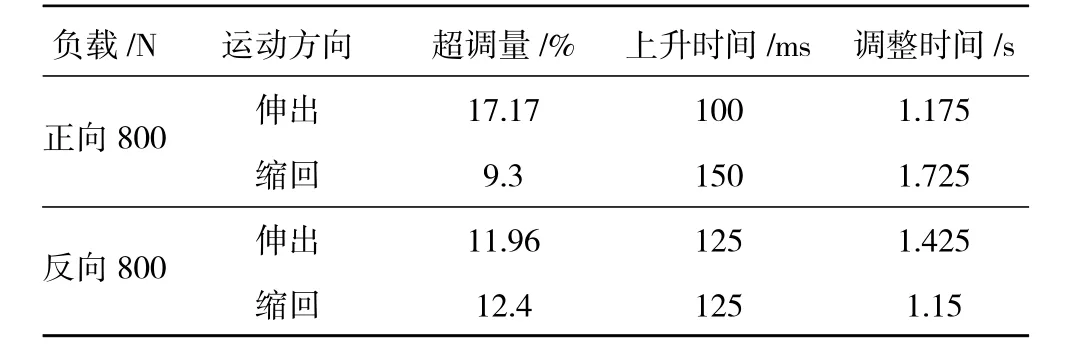
表2 不同負載下階躍響應試驗數據統計
通過數據對比可以發現:正向負載會導致作動筒伸出和縮回時出現明顯的動態特性差異,而反向負載的差異則不是很明顯,當負載超過FL0時,作動筒縮回時的動態特性要“快”于作動筒伸出時的動態特性,即縮回增益大于伸出增益。試驗結果與理論分析結論一致。
3 結論
本文基于閥控不對稱作動筒結構和電子控制模塊、傳感器模塊的分析,提出了1種典型航空發動機作動筒的伺服控制建模與分析設計方法,并通過實際發動機導葉位置控制系統的應用與驗證,得到以下結論:
(1)通過模型與試驗數據在時域和頻域的結果對比可知,基于閥控不對稱作動筒結構的伺服控制系統建模與分析設計方法切實可靠,模型置信度高,對實際應用具有指導意義。
(2)通過理論和試驗數據的統計分析可知,作動筒應盡量提供反向負載,且負載力應盡量在FL0附近,這樣可使作動筒往返控制效果一致,有利于伺服系統的控制。

