模糊-隨機混合參數的機構運動可靠度計算方法

游令非， 張建國,*， 翟浩， 李橋

(1. 北京航空航天大學 可靠性與系統工程學院, 北京 100083；2. 北京航空航天大學 可靠性與環境工程技術國防科技重點實驗室, 北京 100083)

機構運動時變可靠性是現有機構可靠性理論的重要內容，機構運動時變可靠度定義為在規定的運動區間上，規定的運動環境中，機構完成規定動作的能力，數學中表示為機構的實際運動輸出滿足期望運動輸出的概率，即機構運動誤差位于最大允許誤差范圍內的概率，其依賴于機構的運動誤差建模和分析。機構運動誤差問題一直受到機構學研究者的廣泛關注，并提出了諸如最壞情況分析、概率分析和模糊分析等方法。Tuo等[1-2]考慮機構參數的不確定性，建立了機構動態可靠性分析模型，并對連桿機構等典型傳動機構進行了動態精度可靠性分析。董玉革等[3]提出將機構中不確定性因素處理為模糊變量進而構造了機構模糊可靠度分析算法。張義民等[4-5]采用Edgeworth級數方法研究了隨機變量不完全概率信息和隨機變量為任意分布的機構可靠性問題。但上述方法均為靜態可靠性分析問題，并未衡量機構在整個工作范圍內的可靠度。Zhang和Du[6]結合結構可靠性分析中上穿越率和下穿越率概念，推導了計算機構時變運動可靠性解析算法。除此以外，傳統的時變可靠性方法，也可以解決一般的機構運動精度可靠性求解問題，例如PHI2法[7-8]，極值響應面法[9-10]等。但這些研究只限于兩態假設，即非成功即失敗，這并不適用于實際工程應用中由認知不確定性帶來的非兩態問題分析。

基于包絡思想的解決機構運動精度可靠性問題的方法由Du[11]首次提出，其通過誤差帶包絡和一次二階矩方法相結合，解決機構運動誤差時變可靠度的求解問題。Zhang和Du[12]運用包絡函數的方法，對鉸鏈間隙尺寸和結構尺寸同時具有隨機特性的機構進行了時變可靠性分析。Wei等[13]提出了基于包絡函數法的參數可靠性靈敏度分析和全局可靠性靈敏度分析方法，求出了參數可靠性靈敏度指標和全局可靠性靈敏度指標。Wei等[14]利用包絡函數與一次二階矩相結合的方法，針對輸入變量具隨機過程特性的桿系，對整個運動行程進行了可靠度求解。但這些研究并未考慮參數的模糊性，僅考慮了隨機特性，這與實際工程應用是不相符的。

綜上所述，傳統的包絡函數方法雖然可以很好地求解機構在整個工作范圍內的可靠度，但其并沒有考慮普遍存在的認知不確定性問題，特別是一些參數除隨機特性外，往往伴隨著模糊性問題；同時，其并未考慮失效準則的模糊性，即認為產品只有“成功”和“失效”2個狀態，但實際工況中，由于對故障機理、失效模式等的認知不確定性，使得常規“兩態”假設無法滿足實際要求。因此,對于同時具有模糊和隨機特性的機構系統的運動可靠度的研究十分必要。本文在關于機構模糊-隨機時變可靠性研究的基礎上，針對機構運動誤差存在模糊判據和不確定參數具有模糊-隨機混合特性的情況進行可靠性建模分析，對模糊判據和參數進行等效轉化的同時，應用包絡思想對運動誤差帶建立模糊-隨機時變可靠性模型，將時變可靠性問題轉化為時不變可靠性問題，并最終在每一截集下求出相應可靠度并進行平均加權，得到了機構系統運動在全行程內的可靠度，并最終應用于四連桿機構。

1 模糊失效判據的等效

組成機構的構件存在著加工和裝配誤差，這就使得構件的尺寸具有不確定性，從而造成機構運動誤差的不確定性[12]，設g(X,θ)為機構運動誤差，其中X=(X1,X2,…,Xn)為機構構件尺寸隨機變量，θ=θ(t)為機構運動角度，運動誤差定義為機構實際輸出ψ(X,θ)和理想輸出ψd(θ)之差，即

g(X,θ)=ψ(X,θ)-ψd(θ)

(1)

由機構運動可靠度定義[3]可知，若運動誤差不大于機構允許的運動誤差，則認為機構可靠；反之，則認為機構處于失效狀態。機構運動誤差功能函數G(X)可表示為

G(X)=|g(X,θ)|-ε

(2)

式中：ε為運動誤差閾值。相應地，在輸入角θ的范圍為[θ0,θe]上，其時變運動可靠度為

R=P{G(X)<0,θ∈[θ0,θe]}

(3)

但上述處理方法會帶來一些困難，如設機構運動誤差閾值為0.025 mm，則當機構運動誤差為0.025 mm時，機構是可靠的；而當機構運動誤差為0.025 01 mm時，則認為機構不可靠，但這2種情況之間并無本質差別。造成這種矛盾的原因是將完好與失效狀態截然分開，而未考慮中間過渡狀態，即失效和完好這2個概念的外延是模糊的。為解決上述矛盾，更加準確、真實地反映機構的運動可靠性，有必要將模糊數學方法引入機構的運動可靠性分析中。

失效邊界(誤差閾值ε)定義為某一模糊區間[zL,zU]，其中zL和zU分別為模糊區間的下界和上界，把機構運動誤差失效準則看作模糊事件，描述事件狀態程度隸屬函數μG(z)可以用來表示這一過渡情況，其數值越大，事件失效的傾向越大，數值越小，失效的傾向越小。機構運動失效概率可表示為

(4)

式中:z為機構模糊-隨機混合空間Ω中的隨機變量，其概率密度函數為fG(z)；μG(z)為描述事件狀態程度的隸屬函數，其范圍為0≤μG(z)≤1。

若μG(z)為遞減函數，即使得機構運動的失效程度隨z值的減小而增大，根據文獻[15]，結合隨機變量的概率分布函數的定義，可以把1-μG(z)看作一個新的隨機變量(記為Z′)概率分布函數，模糊-隨機失效域可以描述為{X|G(X)≤Z′}，等效的功能函數為Ge=G(X)-Z′。

若μG(z)為遞增函數，則可以把μG(z)看作一個新的隨機變量(記為Z″)概率分布函數，同理，這種情況下機構運動的失效域描述為{X|G(X)≥Z″}，對應的等效功能函數為Ge=Z″-G(X)。

2 運動可靠度的一般包絡方法

對于機構輸入角范圍為[θ0,θe]，由X的隨機特性易知在誤差閾值ε下，g(X,θ)=ε實為一族曲線，包絡法[11]定義了對[θ0,θe]上運動誤差曲線族g(X,θ)=ε中所有曲線的包絡，定義包絡方程G+(X)=0和G-(X)=0分別對應上界包絡和下界包絡，即曲線族的上邊界和下邊界，機構運動誤差的包絡函數如圖1所示[12]。由定義知在包絡曲線上，函數值應處處等于ε，同時由于包絡曲線包絡了不同θ下的曲線，所以其對θ求偏導應為0。

在包絡方程給出之后，考慮在整個運行周期中的機構運動誤差時變可靠性問題，可表示為

R(θ0,θe)=Pr{S+∩S-}

(5)

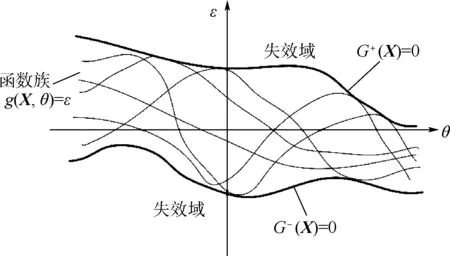
圖1 機構運動誤差的包絡函數Fig.1 Envelope functions of mechanism motion error

式中：S+={G+(X)<0}；S-={G-(X)>0}。

上邊界包絡方程G+(X)=0為

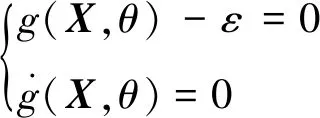
(6)

下邊界包絡方程G-(X)=0為

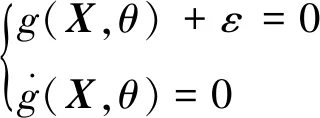
(7)

由以上分析可知，可對每個包絡方程的2個式子進行聯立進而消除θ，時變可靠性問題則轉變為時不變可靠性問題。

3 模糊-隨機時變可靠性建模

考慮具有模糊-隨機混合不確定性的機構，在其輸入角范圍[θ0,θe]內，其運動誤差可表示為

(8)

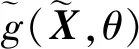
結合前文所述，其模糊-隨機時變運動可靠性功能函數可表示為

(9)

圖2 運動誤差的失效隸屬度函數Fig.2 Membership function of motion error failure

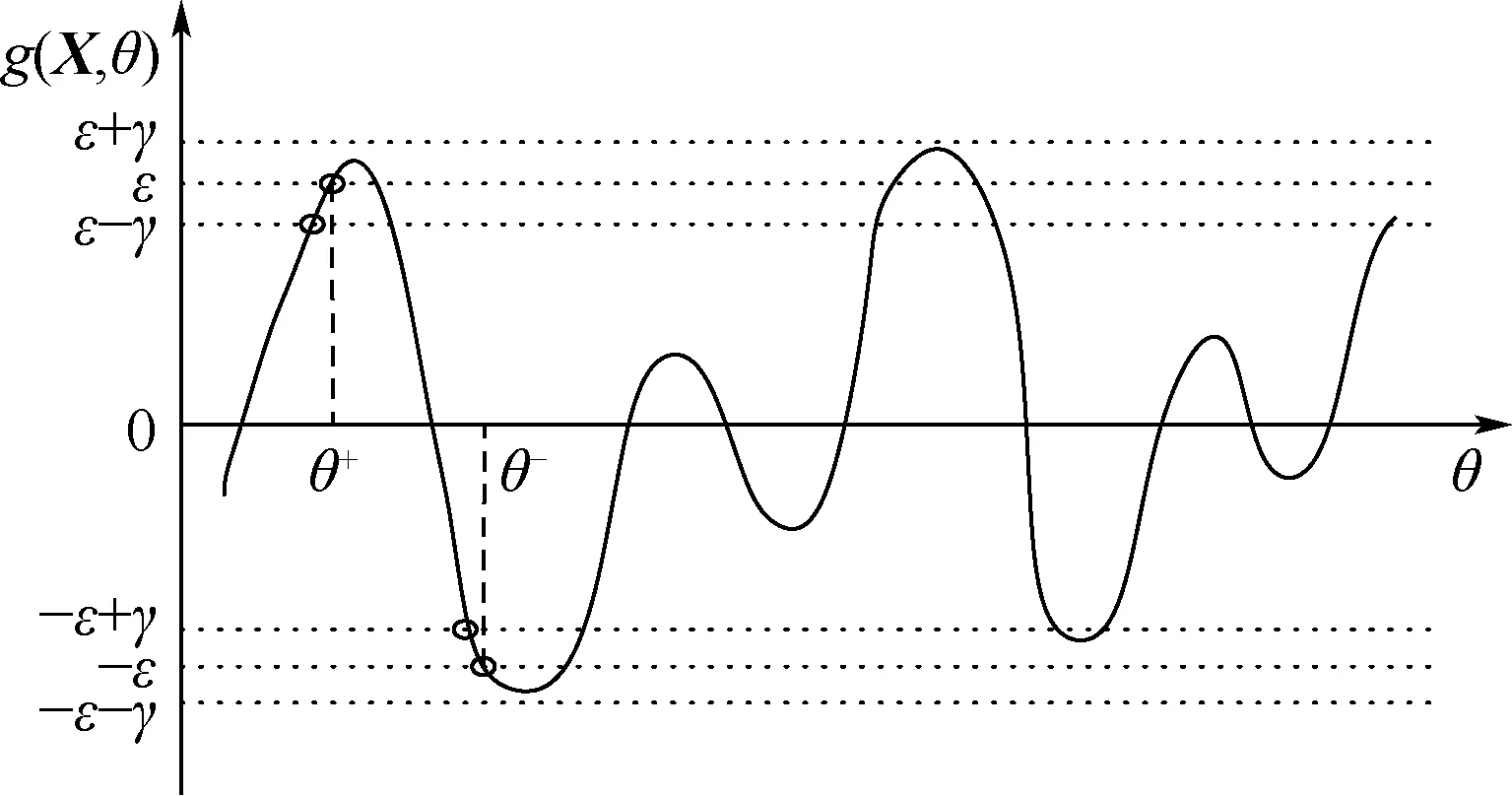
圖3 閾值模糊的時變可靠性失效事件描述Fig.3 Failure event description of time-dependent reliability based on fuzzy threshold

至此，在含有模糊-隨機混合變量和模糊判據情況下，α水平下的機構運動的可靠度為

Rα(θ0,θe)=P{-ε-Z≤g(Xα,θ)≤ε+

Z,?θ∈[θ0,θe]}|=|P{|g(Xα,θ)|≤ε+

Z,?θ∈[θ0,θe]}

(10)

后續通過對α的離散求和或數值積分可以求得機構運動的失效概率。

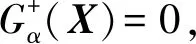
(11)

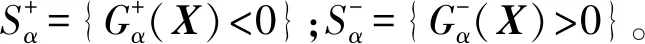
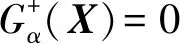
(12)

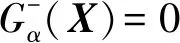
(13)

此時，通過改進包絡方程，功能函數已轉變為僅含參數α的隨機變量的表達式，但繼續通過聯立消除θ的方法，一般很難獲得其精確的解析表達式，下面用近似方法對包絡函數進行求解。

4 基于改進包絡函數的時變可靠度計算

4.1 模糊-隨機時變可靠度的近似求解

由于包絡函數一般具有較強的非線性特性[15]，若通過傳統的可靠度求解方法，即在一個展開點展開構造其近似表達式，會導致與原式誤差較大。為充分利用包絡函數特性，將包絡函數在多個展開點上分段線性化，構造近似包絡函數并求出每段的展開點，最終通過求這些展開點的聯合分布函數最終求得可靠度。

假設Xα=[X1α,X2α,…,Xnα]為相互獨立的正態分布隨機變量，對g(Xα,θ)-Z在Xα的均值μXα處用一階泰勒級數展開來近似運動誤差，并把Xα化成標準正態隨機變量U，展開后表達式記為Lα(U,θ)，則由式(12)與式(13)知：

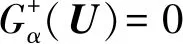
(14)

(15)

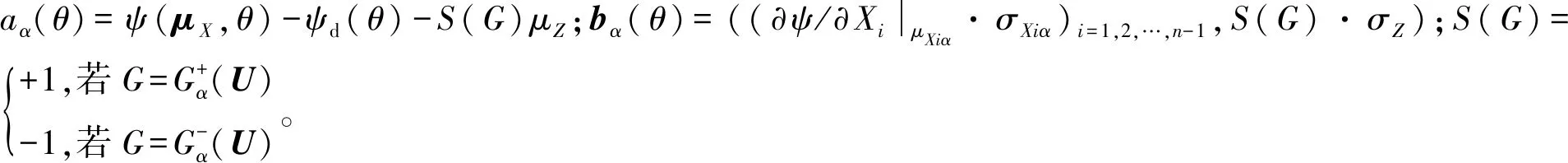
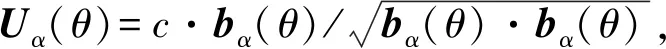
另一方面，由式(14)與式(15)可知，近似運動誤差S(θi)Lα(U,θi)為正態分布，由此可以用展開點的高維正態分布函數(均值μα和協方差陣Σα)對失效概率進行數值求解：

μα=(s(θi)μLα(θi))i=1,2,…,m=

(S(θi)aα(θi))i=1,2,…,m

(16)

Σα=(σij)i,j=1,2,…,m

σij=s(θi)s(θj)bα(θi)bα(θj)

(17)

S(θi)=

(18)

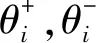
Pfα(θi)=Pr{s(θi)Lα(U,θi)>ε}=

(19)

(20)

將α在[0,1]上離散n等份，則閾值為ε下的可靠度可表示為

(21)

特別地，若α連續且所有水平中去除的多余展開點均相同，則閾值為ε下的可靠度可表示為

(22)

4.2 算法流程

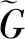
步驟2將α在[0,1]上離散n等份，α初始化為0。將步驟一的結果轉化成α水平下的僅含隨機變量的功能函數Gα。

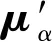
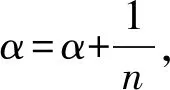
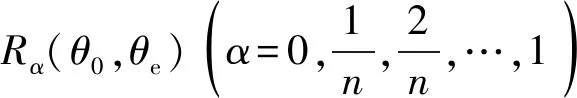
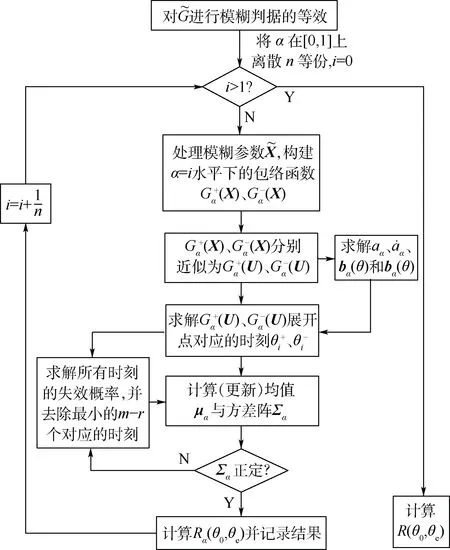
圖4 基于改進包絡函數的可靠度計算方法流程Fig.4 Flowchart of reliability computation method based on advanced envelope function

5 四連桿機構運動可靠度計算

5.1 四連桿機構運動學建模與分析

本例用本文方法對四連桿機構進行運動可靠度分析，首先，對四連桿機構進行運動學建模。在二維空間F(x,y)中，機構如圖5所示，輸入角為θ，輸出角為ψ。

(23)

首先考慮模糊判據，根據第1節的分析，將模糊閾值等效為隨機變量，本例γ取0.01，對比式(10)及分析可知，應引入隨機變量Z，它的概率累積分布函數為

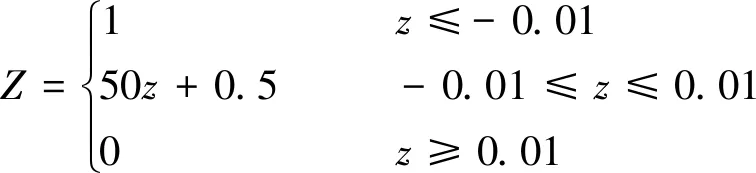
(24)

(25)

則α水平下的概率密度函數為

fα(r2)=

(26)

則α水平下R2的均值和標準差分別為

圖5 四連桿機構Fig.5 Four-bar linkage mechanism

Eα(r2)=5

(27)

(28)

其運動輸出方程組在α水平下的表達式為

(29)

由式(27)和式(28)可得α水平下尺寸隨機變量分布的數字特征，如表1所示。

表1 α水平下尺寸隨機變量的數字特征Table 1 Numerical characteristics of random dimension variables under α level

通過以上對模糊變量的等效，由式(23)解得α水平下的ψ(Rα,θ)為

(30)

式中：

A=-2R1R3sinθ

B=2R3(R4-R1cosθ)

進而由式(15)可得求得b=(b1,b2,b3,b4)。

5.2 四連桿機構模糊-隨機時變可靠度求解

如圖5所示的四連桿機構理想的運動方程為

ψd(θ)=90+7.13sin(2(θ-95.5))

輸入角范圍為[θ0,θe]，其中θ0為0°，θe為90°，則其理想運動輸出ψd(θ)為輸入角從0°～90°間輸出端的角度。

在可變閾值ε上，用本文提出的計算方法和蒙特卡羅仿真(Monte Carlo Simulation，MCS)法的結果進行比較，其中，由于蒙特卡羅法的仿真次數規模為107級，認為其計算結果是趨于真實值的。

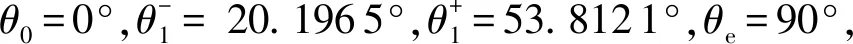
由式(20)可得可靠度R1(θ0,θe)=0.313 3。其余截集水平下的可靠度結果重復以上步驟即可，計算結果如圖7所示。將其平均加權即為ε=0.5時的運動可靠度。

當ε在[0.2,1.4]上變化時計算結果如圖8所示，由失效概率曲線圖表明本文提出的模糊-隨機時變可靠度計算方法與MCS法在失效概率的計算上差別較小，計算結果準確度可以認為滿足機構運動誤差的分析要求，對工程實際應用有一定的參考價值。部分誤差閾值對應的結果見表2。

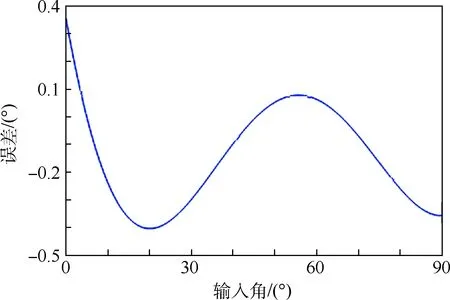
圖6 變量取均值時的運動誤差變化Fig. 6 Motion error change at means of variables

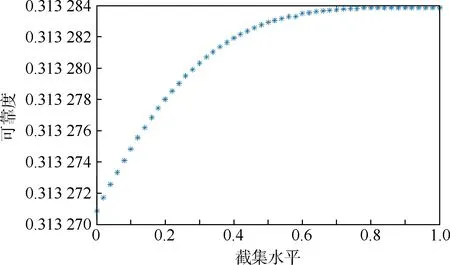
圖7 ε=0.5時可靠度隨截集水平α的變化Fig.7 Change of reliability with cut set level α when ε=0.5

圖8 0°～90°的失效概率Fig.8 Probability of failure at 0°-90°

ε/(°)本文方法MCS法0.700.714250.713830.800.836450.836110.900.914070.913671.000.958250.957941.100.981310.981031.200.992320.99218

從計算結果可以看出，基于本文方法所得的結果均略大于MCS法的結果，這是因為MCS法是對所有時刻(角度)進行遍歷并進行求解，而基于本文提出的方法是對有限的、失效概率較大的展開點進行計算，所以可靠度計算結果均比MCS法略大一些。

6 結 論

本文針對機構產品的時變可靠性建模分析問題，綜合考慮了模糊性和隨機性，針對機構運動誤差建立了機構運動模糊-隨機時變可靠性模型，提出了模糊-隨機時變可靠度求解方法，經案例驗證表明：

1) 本文提出的模糊-隨機時變可靠度求解方法相較于傳統時變可靠度求解方法，不但考慮了參數的模糊性，同時還考慮了判據的模糊性，解決了模糊-隨機混合參數下的機構時變可靠性問題，更符合實際工程應用，對類似的機構運動可靠性分析具有一定的指導意義。

2) 本文方法求解方便，相比于MCS法計算誤差較小，本案例中2種方法的計算誤差最大不超過0.000 8，貼合度較高；同時計算效率大大提高，每α水平下MCS法計算次數為107次，而本文方法為50次左右。

3) 本文提出的機構運動模糊-隨機時變可靠性分析方法適用于隨機樣本不完善，或樣本數量不夠的情況，可計算出較精確的結果。