基于制動轉向協同控制的智能車緊急避障研究*

王其東，李印祥，陳無畏，趙林峰，謝有浩

（1.合肥工業大學汽車與交通工程學院，合肥 230009； 2.合肥學院，合肥 230601； 3.安徽獵豹汽車有限公司，滁州 239064）

前言

隨著科技的進步，人們不再滿足于傳統車輛所提供的功能，與此同時能夠輔助人或者取代人做決策的智能車成為了近幾年的研究熱點，車輛主動安全技術的研究和開發也引起車輛研發人員的重視［1］。文獻［2］中對車輛在直道行駛時前方障礙物突現的操作特性進行了研究：在車速低于60 km／h的低速工況，駕駛員習慣于制動和轉向同時作用控制汽車；在車速高于80 km／h的高速工況，駕駛員更偏向先采用純制動來降低車速。文獻［3］中對駕駛員緊急變道的操作特性進行了研究，分析了這個過程中轉向盤轉角和制動力隨時間的變化關系，并據此搭建緊急避障最優操作模型。日本京都大學的O.Nishihara提出一種綜合了轉向和制動的最小化車輛總動力的最優控制方法，仿真結果表明該方法可快速有效地解決避障問題［4］。考慮到換道過程中行車的平順性和安全性，M.Ruder等［5］開發了一套輔助換道系統（highway lane change assistant monitor，HLCAM），該系統能對環境中的危險情況進行判斷，并自動警告駕駛員注意，如果駕駛員并未進行操作，則系統主動地進行轉向躲避障礙物。U.Rosolia等人［6］提出一種采用NLMPC控制器來跟蹤避障路徑的方法：首先通過GMRES／Continuation algorithm規劃出轉向避障時的路徑；然后建立1／4車輛模型和1／2車輛模型用非線性模型預測控制方法來跟蹤期望的避障路徑；最后計算出這兩個車輛模型跟蹤偏差，用PID控制來縮小這兩種車輛模型的跟蹤誤差。劉英杰等［7-9］采用模型預測控制算法對規劃的理想軌跡進行跟蹤，且都驗證了這種方法的有效性。A.Khajepour等人［10］利用三維虛擬危險勢場，產生出車輛避障安全行駛路徑，并利用多約束模型預測控制來跟蹤這個安全路徑，最后通過Carsim和Simulink聯合仿真證明了該方法對許多駕駛情況的有效性。弗雷德里克大學的S.Kanarachos［11］提出了一種新的用來計算避障最優轉角的方法—一種基于改進Pontryagin極大值原理和Bang-Bang控制的方法，這種方法將轉角最優轉化為可調整的時間最優問題；仿真結果表明該方法與其它方法相比，雖然計算速度較快，但對于車輛不同行駛工況適應性較差。南京大學的Chen Y.等［12］提出一種智能車ACC和自動換道集成控制方法，該方法將換道算法分為兩種：一種是高速情況下的自動換道；另一種是主動避障時的主動換道。日本東京大學的I.Kou等人［13］基于線控主動轉向提出一種輔助換道控制策略，該方法通過分配人和車之間的主權系數，實現人機共駕。文獻［14］中提出了一種智能車輛方向和速度綜合決策的混合機理與規則建模研究，將縱向加速度和側向加速度分成若干個組合，求出不同組合下對應的路徑，根據環境約束條件，從中選擇一條最優的路徑，并采用穩態預測動態校正理論跟蹤最優的加速度路徑。該方法雖然能規劃出最優的路徑，但由于縱向加速度和側向加速度組合過多，造成計算量大、實時性難以保證等問題。

綜上所述，以上對于車輛主動換道避障的研究中，大多數學者假設汽車換道過程中速度是恒定的，忽略了車輛縱向速度的變化對車輛換道過程的影響，但車輛在高速緊急換道時，縱向速度的變化對換道安全性影響巨大。因此，本文中綜合考慮了車輛避障過程中縱向和側向速度的變化，將車輛避障看成是通過調整合適的車輛合力而使避障距離最短問題。假設車輛初始時刻偏航角為0，側向避障距離一定，建立車輛避障過程狀態方程和約束條件，然后利用拉格朗日乘子法，以車輪與地面附著條件為約束，求出車輛緊急換道避障過程中的理想縱向力和側向力隨時間的變化規律和相應的避障路徑，然后建立車輛3自由度動力學模型，并基于Carsim和Simulink硬件在環試驗和實車試驗來驗證其有效性。

1 最優控制量求取

1.1 緊急避障操作行為分析

一般來講，在目標車道沒有障礙物，滿足換道避障條件時，駕駛員可進行換道避障。駕駛員在緊急換道避障時一般會發生以下兩種碰撞情況：

（1）由于駕駛員在危險情況下比較緊張等心理因素的影響，會對車輛進行激烈的轉向和制動操作，從而可能出現雖并未與當前車道的障礙物發生碰撞卻由于車輛行駛到目標車道時已發生失穩，與目標車道正常行駛的車輛發生了碰撞；

（2）由于駕駛員發現前方障礙物時，距離已較近，由于轉向系統等限制，車輛無法完成避障，與當前車道前方的障礙物發生角碰。

對于第一種碰撞情況，主要是因為駕駛員無法在緊急的情況下判斷出最優的操作方式組合，而導致即使已經裝備車身電子穩定系統（ESP）的車輛仍舊發生失穩。

對于第二種碰撞情況，一方面是駕駛員對于前方避障安全距離存在錯誤判斷，另外一方面是車輛轉向系統硬件結構的限制導致車輛無法產生足夠大的轉向角完成快速換道避障。

對以上汽車緊急避障時車輛發生碰撞的原因分析可將其分為兩大類：主觀因素和客觀因素。主觀因素即駕駛員對車輛避障時候安全狀態、最優轉向盤轉角和制動力的判斷錯誤；客觀因素即為汽車固有結構。

對于智能車，無需考慮客觀因素的影響，緊急避障操作由車輛自身完成，這就需要決策出保持車輛穩定躲避障礙物的理想前輪轉角和制動力的變化規律。

車輛的避障過程分為如圖1所示4個階段。

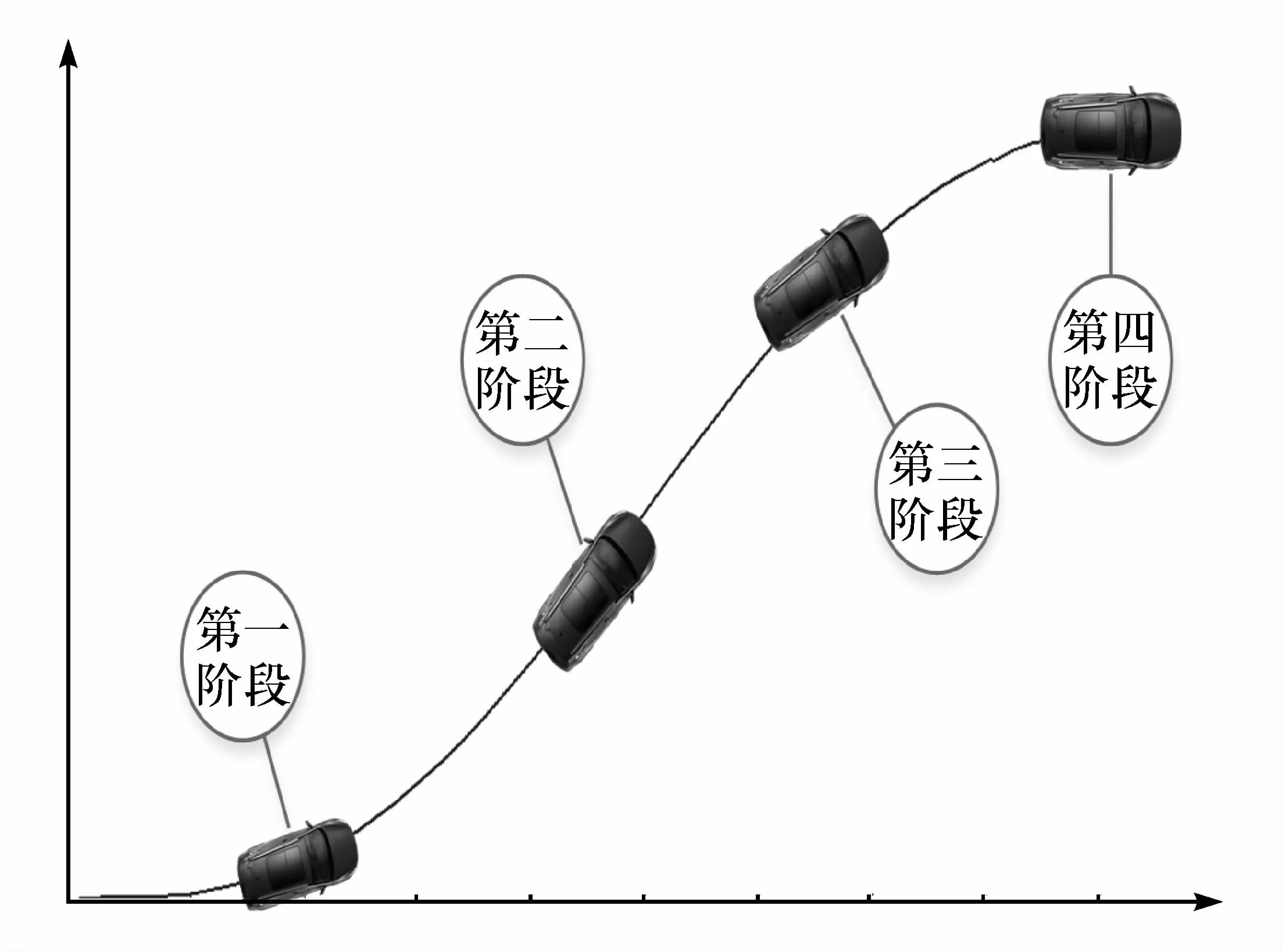
圖1 車輛緊急避障過程

第一階段是車輛制動的同時前輪轉角從初始位置向左轉到最大值的階段，在該避障階段中，車速一般較高且前輪轉角變化速度相對較快，車輪的側偏角逐漸增大，最容易發生側滑。

第二階段是車輛前輪轉角從最大值逐漸回正的過程，該過程中車輛的側偏角是一個逐漸減小的過程，從汽車失穩特性來講，該階段一般不會發生失穩。

第三階段與第一階段類似，是前輪轉角向右轉到最大值的過程，該過程中車速雖有一定程度的降低，但仍是輪胎側偏角增大的過程，也有可能發生失穩。

第四階段與第二階段類似，也是前輪轉角逐漸減小的過程，如果車輛在前幾個階段沒有發生失穩，那么該階段一般也不會發生失穩。

綜上所述，車輛在避障的第一個階段，即制動的同時轉向盤緊急轉到最大角度時，該階段由于速度較快，很容易造成由于輪胎不能提供滿足車輛轉向的側向力而使車輛發生側滑。本文中假設側向換道寬度一定，建立車輛運動狀態方程，將地面所能提供的最大合力作為約束，以最短的縱向避障距離作為性能指標，求解出這個過程中理想的縱向力、側向力的變化規律以及理想軌跡。

1.2 換道模型

車輛換道操作示意圖如圖2所示。圖中：車輛換道起始時刻縱向速度為vx0，側向速度為vy0，航向角為零；車輛換道終止時刻為te，此時車輛縱向速度為vxe，側向速度為vye，航向角為零；車輛行駛的縱向距離為xe；側向距離為ye。

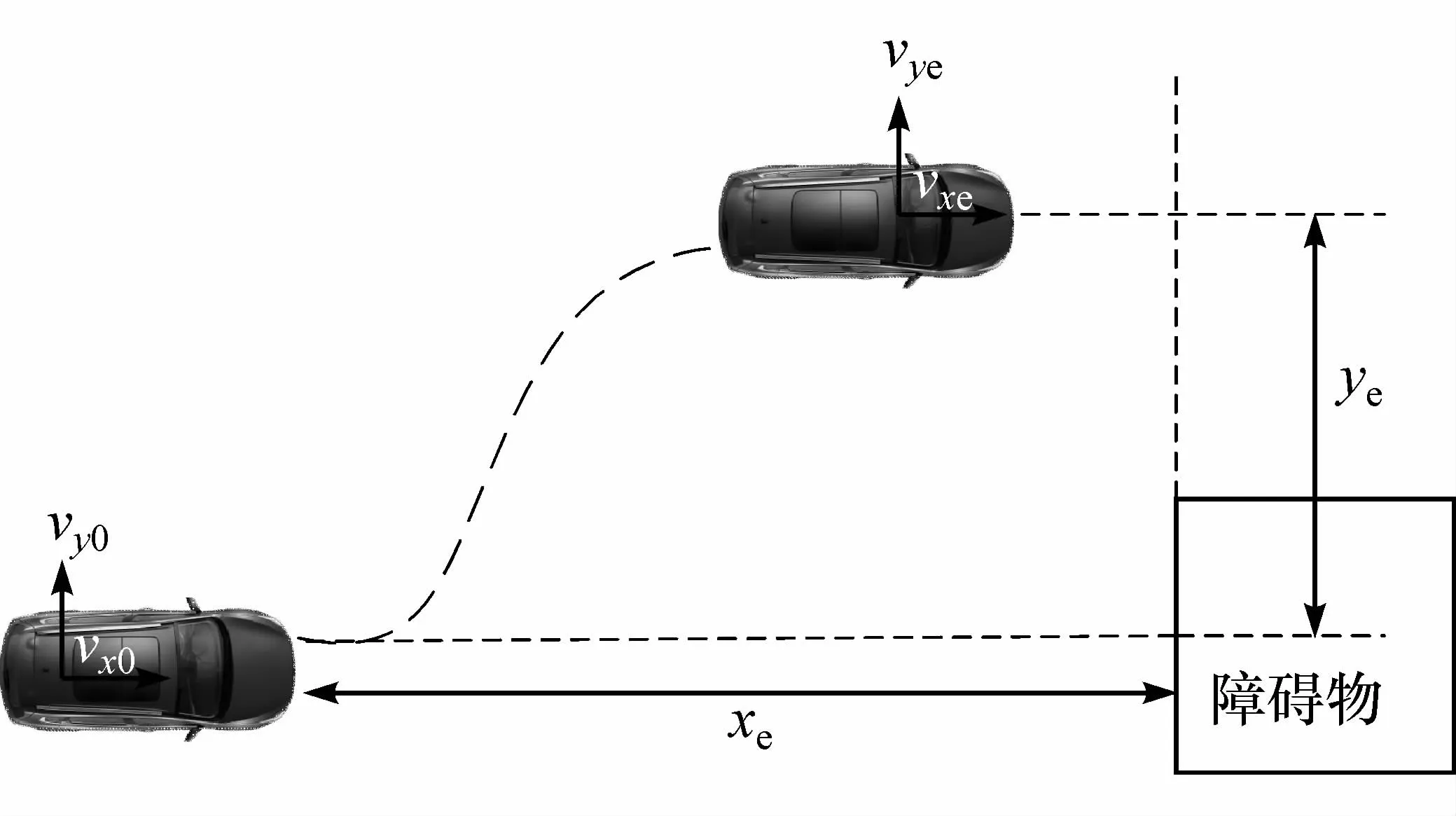
圖2 換道操作示意圖

將整車假設成質量集中的系統，假設在這個過程中，縱向力為 Fx（t），側向力為 Fy（t），根據文獻［15］和文獻［16］，輪胎所能提供的最大側向力和縱向力是一個與路面附著系數和輪胎自身特性相關的參數，其最大縱向力和側向力大致滿足摩擦圓的關系，即

式中Fmax為輪胎力的最大值。

假設轉向制動避障時的控制輸入為

動力學方程為

式中：m為整車質量；x和y為車輛的位置坐標。

對于緊急避障問題，系統的狀態和輸入可用如下公式表示：

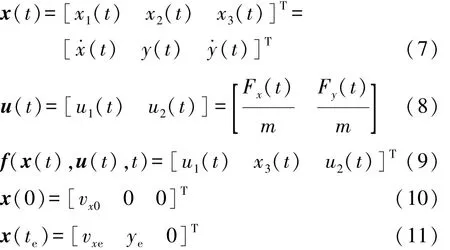
根據文獻［15］中關于緊急避障中最小合力的討論，造成車輛失穩的主要原因是輪胎路面限制，輪胎無法產生足夠大的汽車轉向側向力導致車輛失穩。因此，在以上建立車輛換道模型基礎上，將輪胎路面附著力作為約束，利用拉格朗日乘子法和哈密頓函數求出帶有路面附著約束的車輛行駛最優控制力。最終將避障中理想縱、側向力的求取轉換成求解拉格朗日乘子系數υ1，υ2和避障完成時間te這3個參數的問題。

式中φ（t）為車輛避障過程中航向角。從式（13）～式（16）可以看出，只要車輛初始縱向速度vx0、側向換道寬度ye、車輛最大合力Fmax和質量m確定，就可求出 te，υ1，υ2這 3個參數，進而根據式（17）和式（18）可求出理想的縱向力和側向力輸入。

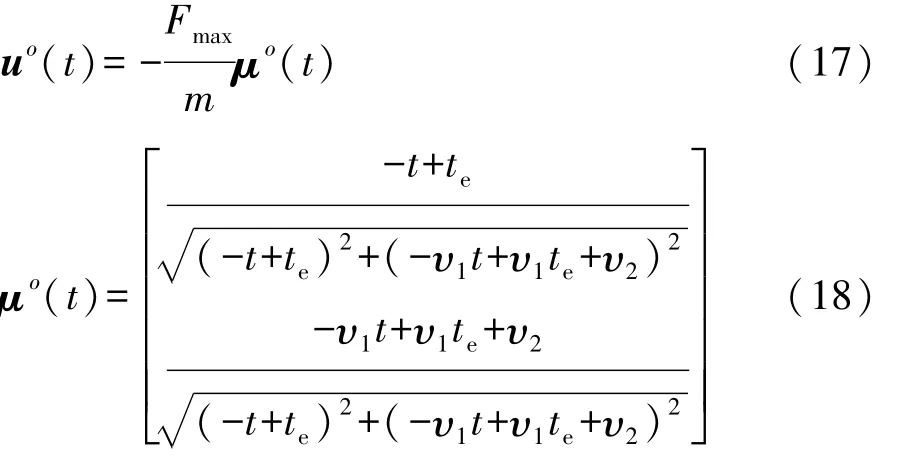
仿真中設置路面附著系數為0.8，整車質量為825 kg，最大合力為6 468 N，車輛換道寬度為3 m，初始速度為80 km／h。

將上述車輛仿真參數代入式（13）～式（16）中得

將式（19）中參數代入式（17）和式（18）中得到理想的縱、側向力變化規律和理想軌跡。圖3所示為理想的縱向力和側向力變化規律，圖4所示為理想的車輛軌跡。

圖3 理想縱向力和側向力的變化規律

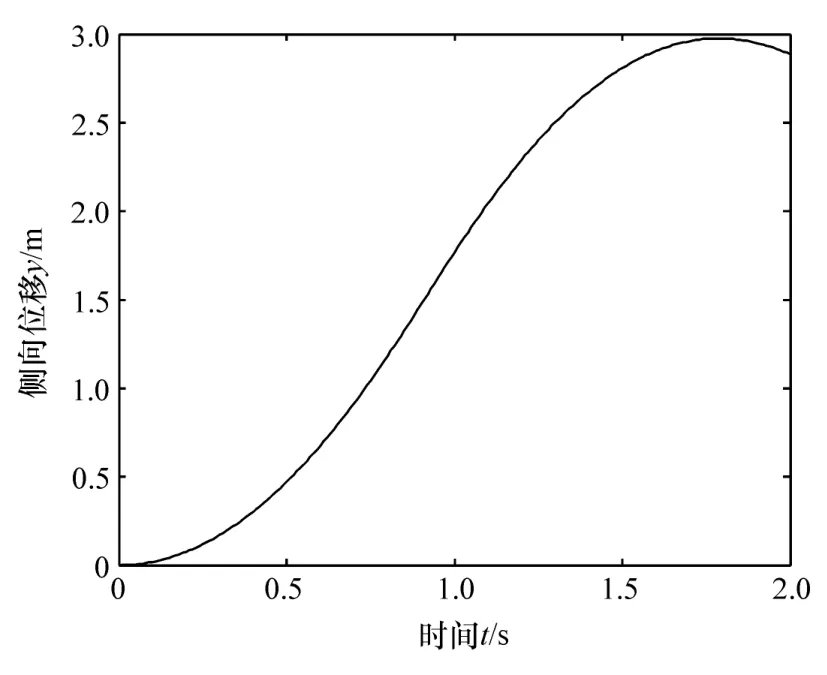
圖4 理想的車輛軌跡

2 理想縱向力和側向力的驗證

為驗證理想縱向力和側向力變化規律的有效性，將車輛模型簡化為具有縱向運動、側向運動和橫擺運動的3自由度單軌車輛模型，對車輛進行了一系列理想化的假設：

（1）假設車輛在平坦路面上行駛，懸架系統和車輛是剛性的，忽略車輛垂向運動和懸架的影響；

（2）忽略空氣阻力的作用；

（3）假設車輛前輪驅動，忽略轉向系的影響；

（4）假設車輛制動時，軸荷轉移和縱向力的變化比例一致。

3自由度車輛模型如圖5所示。

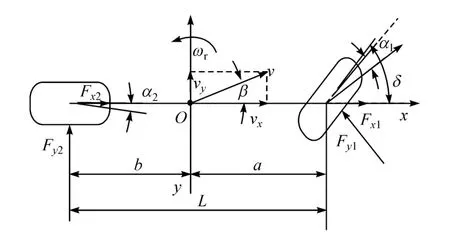
圖5 3自由度車輛模型

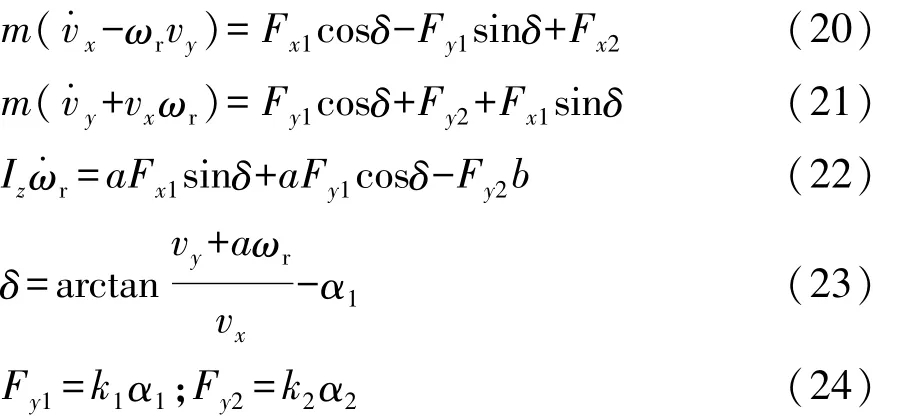
式中：Fx1和Fy1為車輛前輪受到的縱向力和側向力；Fx2和Fy2為車輛后輪受到的縱向力和側向力；vx和vy為車輛縱向和側向速度；ωr為車輛的橫擺角速度；a和b為車輛質心到前軸和后軸的距離；α1和α2為前后輪的側偏角；k1和k2為前后輪側偏剛度；δ為車輛前輪轉角；Iz為轉動慣量。具體參數值如表1所示。

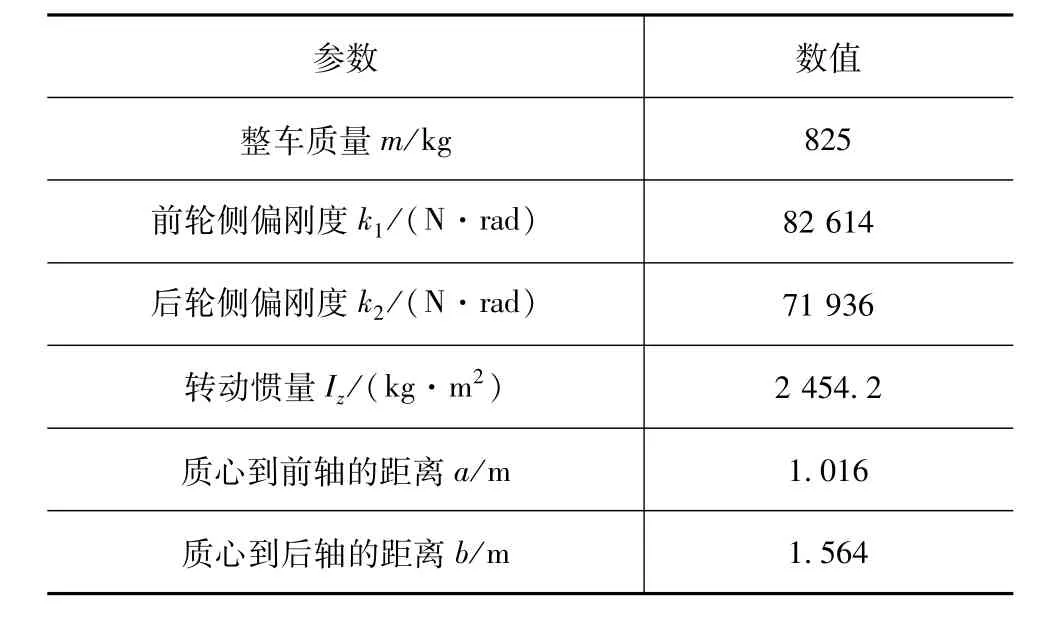
表1 1／2車輛模型參數

設定仿真中路面附著系數為0.8，車輛初始速度為80 km／h。本文中采用了兩種方法進行了驗證：（1）將理想縱向力和側向力的變化規律代入3自由度模型中，觀察其實際運行軌跡；（2）選取幾組固定的縱向力變化規律代入3自由度車輛模型中。通過這兩種方法來觀察其實際的運行軌跡，具體方法如圖6所示。

假設車輛換道過程中速度是恒定的，即地面對于車輪的縱向合外力為定值。而當車輛緊急換道避障時，假設該過程中制動減速度恒定，忽略滾動阻力和空氣阻力，則縱向力恒定。由于輪胎力的限制，車輛的側向力存在一個極限值，表現在車輛操控上，在保證車輛穩定性的前提下，車輛的前輪轉角會有一個極限值。從圖7中可以看出，在當前仿真條件下，當固定縱向力為1 600 N時，相同時刻車輛的側向距離最遠。因此將這個變化規律作為假定縱向速度固定，即縱向力固定條件下的最優規律，其軌跡曲線和理想的軌跡曲線對比如圖8所示。

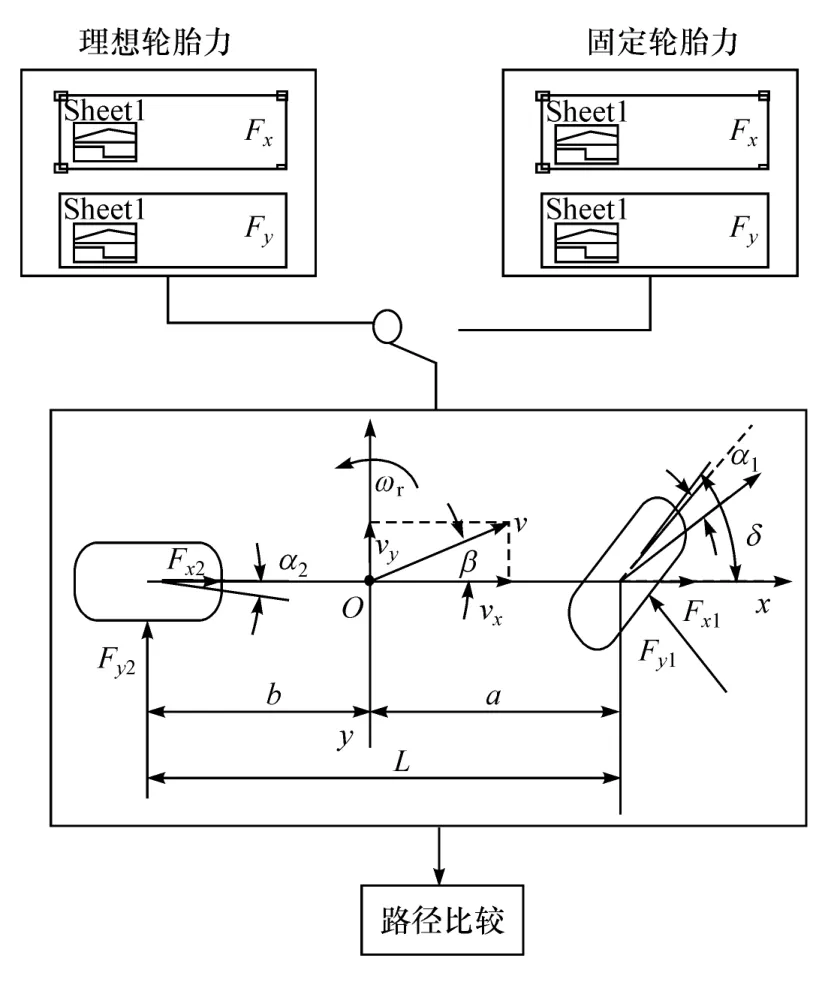
圖6 基于3自由度模型的驗證方法

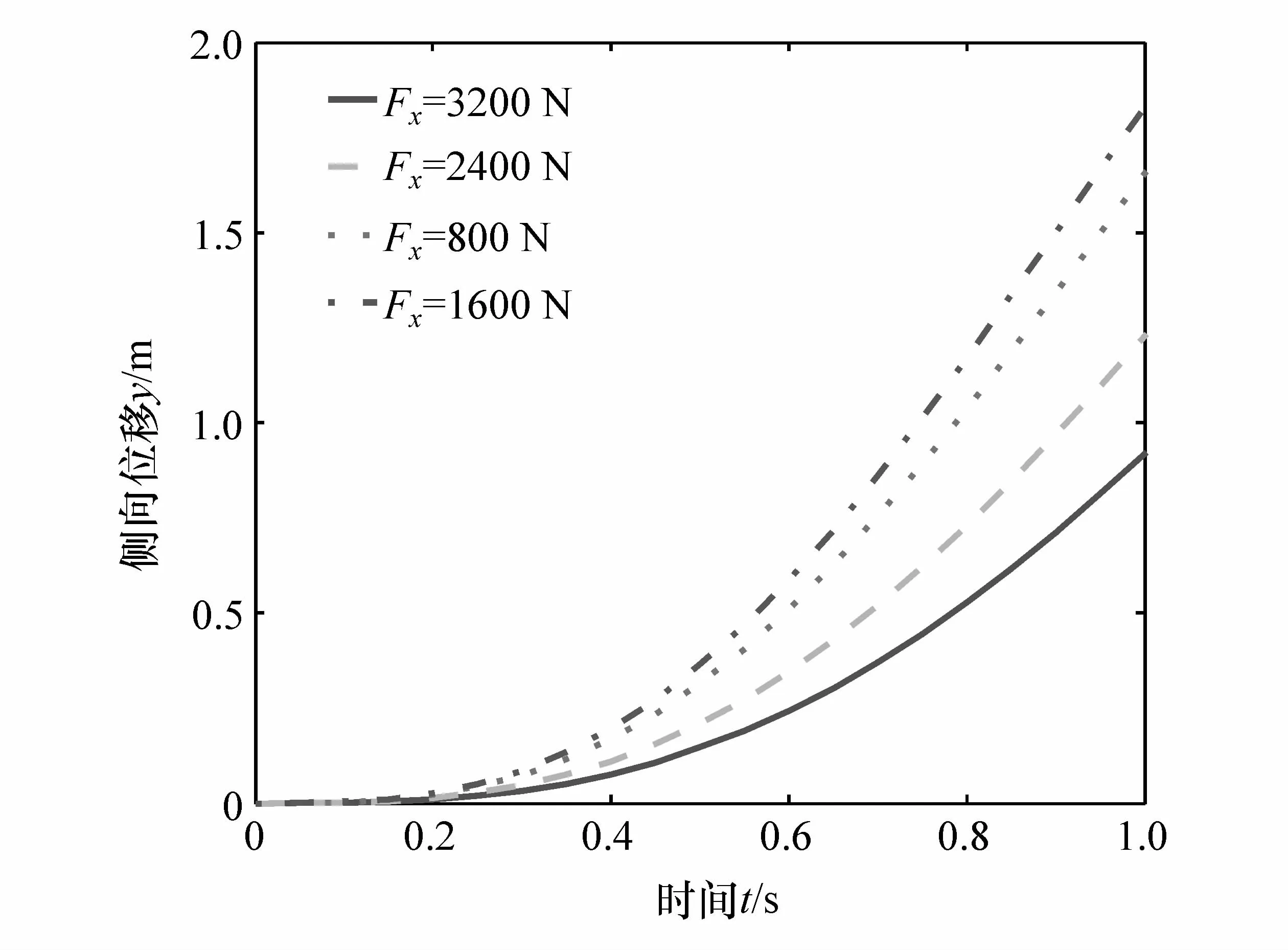
圖7 固定縱向力路徑

從圖8中可以看出，將通過車輛理想2自由度模型計算出的理想縱、側向力變化規律代入車輛3自由度模型時，車輛實際軌跡能夠很好地與理想軌跡保持一致；而假設縱向加速度固定時，即縱向力變化規律固定時，此時的車輛行駛軌跡曲線則和理想的軌跡有相對較大的差距；且采用理想縱向力和側向力時，車輛在相同時刻的側向位移也比固定縱向力時要大，即避障能力要強。

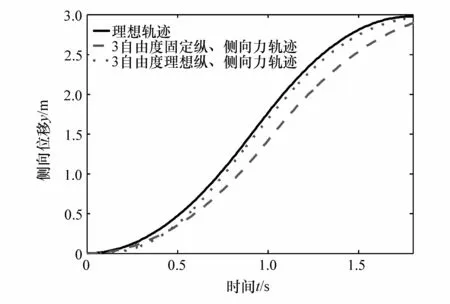
圖8 3種路徑對比圖

3 基于Carsim和Labview的硬件在環試驗驗證

3.1 基于有限元思想的軌跡分割

根據有限元中將復雜問題看成由許多小的單元互聯組成，對每個單元求近似解，然后推導出求解這個域總的滿足條件，從而得到問題解的這一思想［17］，提出一種將理想的軌跡分成若干個小的單元，如圖9所示。每一個小的單元用i＝1，2，…，n來表示，單元i開始的節點用ai表示，結束的節點用bi表示，第k個小單元中開始的節點和上一個單元中結束的節點連在一起，這樣就將一條完整的換道軌跡分成了n個首尾相連的小單元。將每一個單元中起始點和結束點用兩個參數來表示：ai（tai，yai），bi（tbi，ybi）。

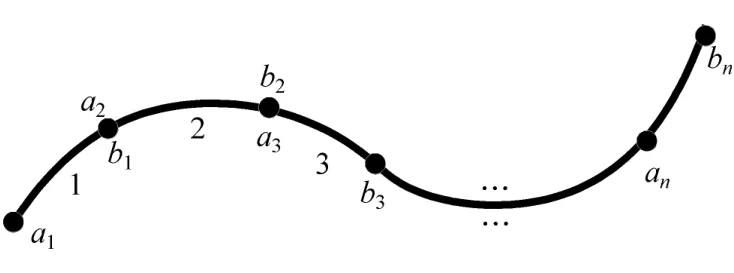
圖9 軌跡分割

3.2 穩態預測動態校正駕駛員模型

將汽車看成一個轉向盤轉角和制動減速或油門加速雙輸入行駛軌跡單輸出的系統，那么車輛未來的行駛軌跡由這兩個輸入變量所決定；若不考慮輪胎等非線性因素的影響，從車輛運動學的角度來說，假如當前時刻的車輛輸入不變，那么就可預測下一

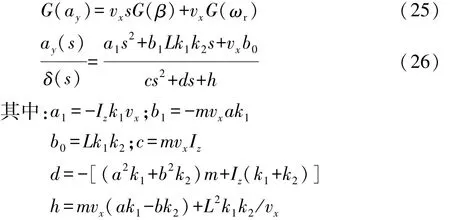
式中L為軸距。

由于穩態預測和實際的車輛運動存在一定的誤差，車輛自身動力學特性又有強非線性等因素，為了補償這些因素的影響，設計PID控制算法對理想的控制輸入做一定的校正。

3.3 路徑跟蹤

為進一步驗證所計算的縱、側向力分配的有效性，采用更加精確的Carsim車輛模型，在Labview中建立基于穩態預測動態校正理論的駕駛員模型，算法大致分為4個步驟：

（1）首先將目標路徑分割成有限個片段，并將各個片段的坐標確定下來；

（2）通過第二個點的坐標確定出初始時刻車輛前輪轉角，當車輛到達該時刻，通過計算實際坐標點和期望坐標點的偏差，對前輪轉角進行第一次修正；

（3）然后將第一次修正的轉角來預測下一時刻車輛的位置，并將該時刻理想的坐標和預測的坐標進行對比，并對前輪轉角進行第二次修正；

（4）最后重復第二、三步驟直到避障過程結束。

算法的具體流程如圖10所示。

3.4 硬件在環試驗

本硬件在環試驗平臺由主動轉向控制器、主動制動控制器、PXI主機、工控機、數據采集卡和CAN卡等組成，同時與車輛動力學仿真軟件Carsim聯合構成車輛主動避障系統硬件在環試驗臺。CAN總線接收轉向盤轉角傳感器信號，數據采集卡采集油門踏板位移信號和制動輪缸壓力信號，并將采集到的信號和計算出來的前輪轉角通過工控機實時傳遞給Carsim中建立的整車模型，實現閉環精準控制。時刻車輛的位置［18］。根據廣義預測理論，預測模型只強調其功能，并沒有對其具體的結構形式有特別要求；而反饋校正則可以對未來的誤差進行補償。就穩態預測而言，利用理想車輛2自由度模型作為預測模型，而軌跡跟蹤就類似于一個滾動優化的過程。根據汽車理想2自由度模型，得到車輛側向加速度到前輪轉角的傳遞函數關系：

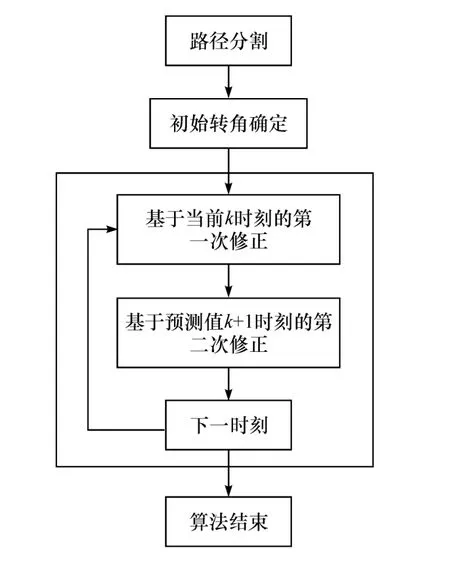
圖10 路徑跟蹤算法流程

硬件在環試驗臺如圖11所示。

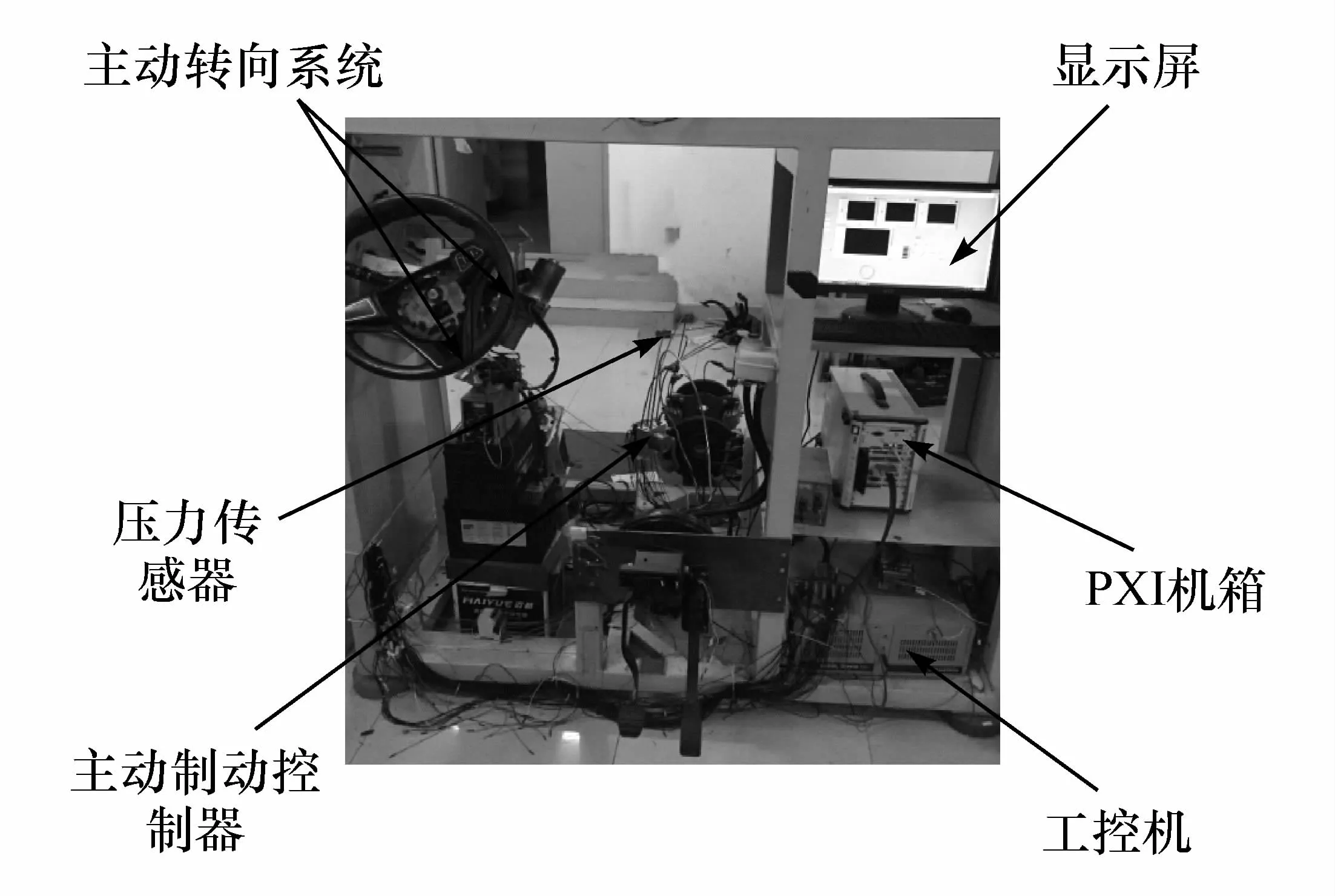
圖11 硬件在環試驗臺

然后在硬件在環試驗臺上，通過Carsim和Labview聯合搭建緊急避障場景，模擬仿真車輛的緊急避障過程。在Carsim中選擇C-class型車，Carsim輸出為車輛位置坐標、橫擺角和車速等信息，輸入為基于駕駛員模型計算的轉向盤轉角信息和理想的縱向力轉換為理想的主缸制動壓力信息。根據Carsim中對于制動系統的研究，汽車縱向力可簡化為主缸壓力的線性函數：

式中：Fx為縱向力；Kb為比例系數；pb為制動壓力。

設定避障初始時刻車速為80 km／h，圖12～圖16分別為硬件在環試驗的主缸壓力圖、速度圖、路徑圖、側向力變化圖和橫擺角速度圖。

圖12 主缸壓力圖

圖13 速度變化圖

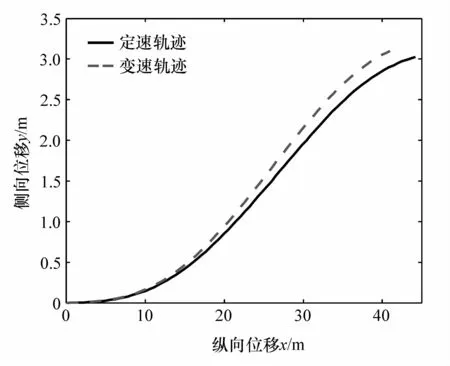
圖14 路徑對比圖

由圖12可見，主缸實際制動壓力值能較好地跟隨理想制動壓力。由圖13可見，車輛在緊急避障換道過程中，隨著縱向制動力的增大，車速下降程度逐漸變得劇烈，在1 s左右時，車輛制動力達到最大，減速度也達到最大，之后制動力又逐漸減小，車輛速度也逐漸趨于平穩，車輛完成換道避障操作。由圖14可見，當車輛換道過程中采用變速，即輪胎縱向側向力按照理想情況變化時，與假定車輛換道過程中速度不變，即縱向力恒定時的行駛軌跡相比，相同的縱向行駛距離時，采用理想縱向力和側向力分配的車輛行駛側向距離要大于車輛固定速度下的側向距離。由圖15和圖16可見，側向力的變化與理想的側向力規律基本保持一致，車輛實際橫擺角速度與理想橫擺角速度保持一致，說明車輛已處于穩態行駛邊緣，表示在該狀態下，汽車避障能力已達到最大，證明了所計算的理想縱向力和側向力分配的有效性。

圖15 側向力對比圖

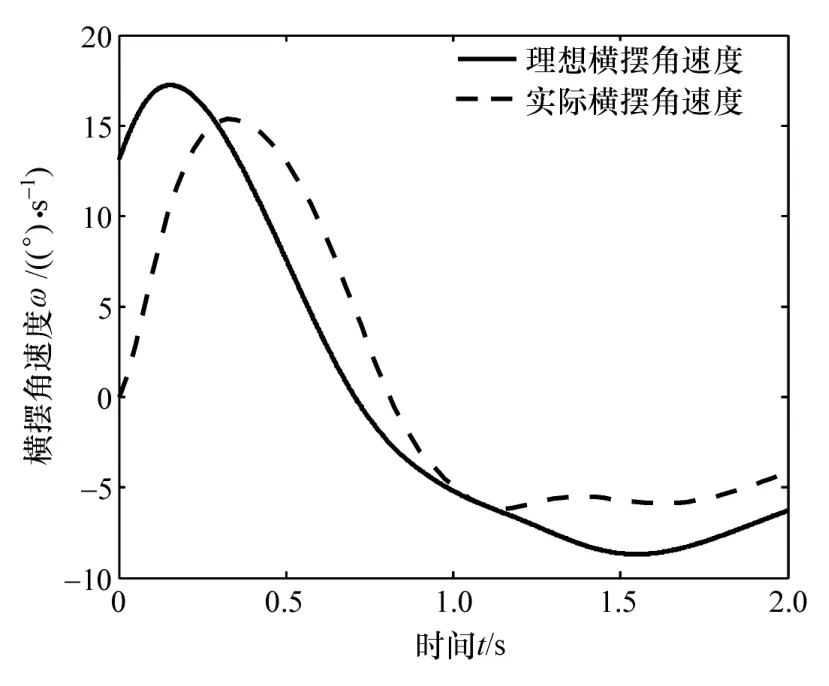
圖16 橫擺角速度對比圖

4 實車試驗

為進一步驗證所提出的制動轉向控制策略的有效性，在試驗車平臺上進行試驗。試驗車平臺如圖17所示，該平臺基于某款電動車進行改裝，將原車的制動部分和轉向部分改裝成能夠進行主動制動和主動轉向的控制系統，車載相機和激光雷達用來對車輛前方的障礙物信息進行識別，陀螺儀和Vbox數采系統對行車過程中的軌跡和橫擺角速度進行記錄。

考慮試驗的安全性，設定實車試驗的初始速度為40 km／h，路面為良好的瀝青路面，由式（13）～式（16）可得當前車輛狀態下參數的計算結果：

試驗結果如圖18～圖21和表2所示。

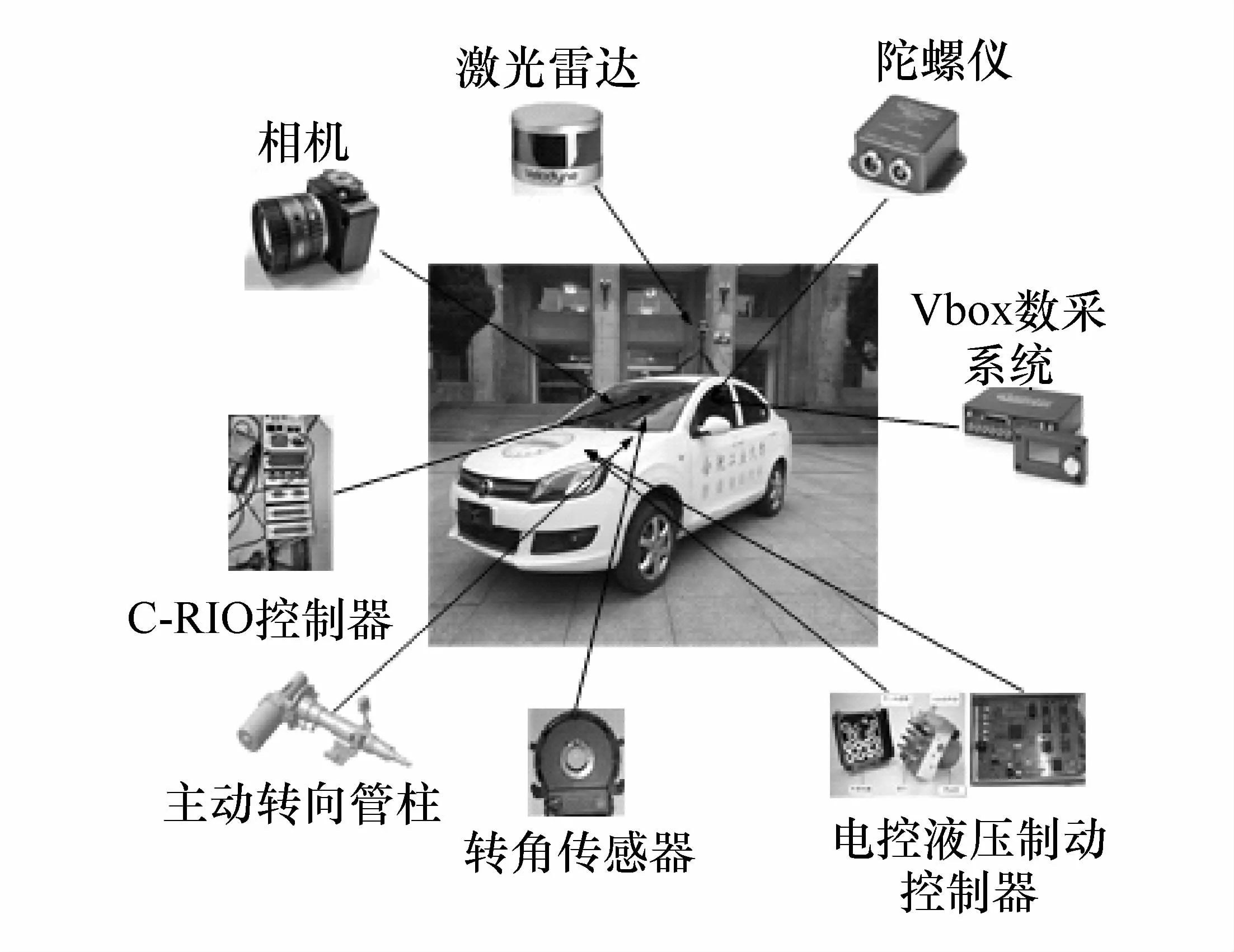
圖17 試驗車平臺

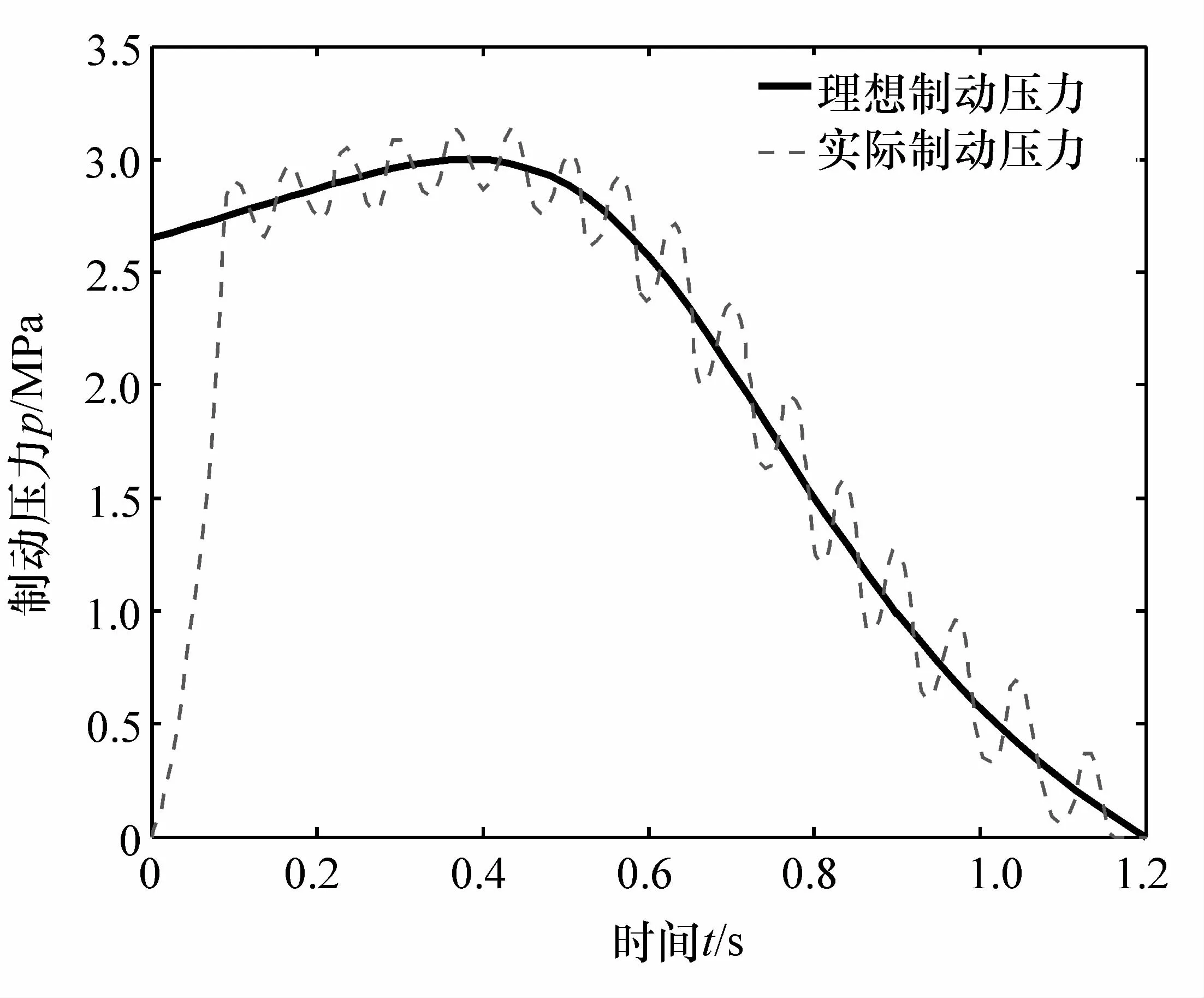
圖18 制動壓力對比圖

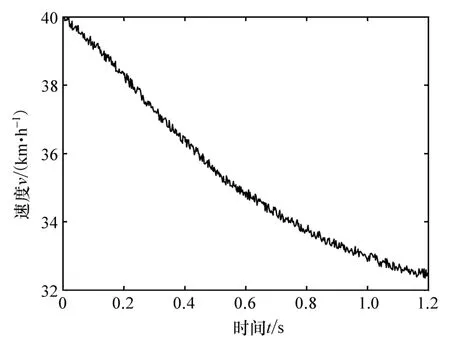
圖19 速度變化圖

由圖18可見，車輛的實際制動壓力先增大后減小，且實際制動壓力能較好跟隨理想制動壓力，在0.5 s左右車輛的減速度達到最大值，車輛的減速度是一個先增大后減小的過程。由圖19可見，在0.5 s之前，車輛的速度下降逐漸加快，0.5 s后車輛的速度下降逐漸變緩。圖20表示了車輛在定速和變速下的避障軌跡曲線。表2列出了車輛在定速避障和變速避障情況下的避障完成時間對比和所行駛的縱向距離對比。由表可見，在相同的換道初始條件和換道寬度的情況下，變速換道規律要比定速換道規律的縱向換道距離短，且完成換道的時間短。圖21表示這個過程中車輛橫擺角速度的變化規律，根據車輛穩定行駛條件，此時的車輛實際橫擺角速度滿足車輛當前行駛條件下的穩態橫擺角速度，即車輛能快速并不失穩地完成換道。

圖20 軌跡對比圖

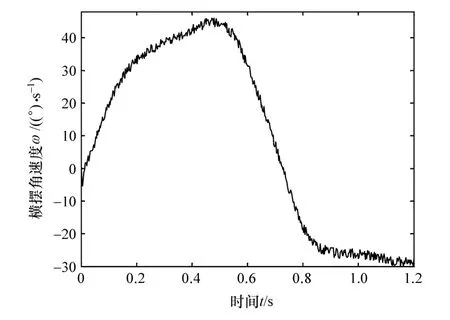
圖21 橫擺角速度

表2 軌跡跟蹤對比

5 結論

（1）本文中從車輛安全性方面考慮了車輛緊急避障時如何快速行駛到相鄰車道，將車輛避障問題看成是避障距離最短問題，并利用拉格朗日乘子法求解出車輛緊急避障時候理想的縱、側向力分配規律以及理想軌跡。

（2）為驗證理想縱、側向力分配規律的正確性，通過建立更加精確的3自由度模型，將理想的縱、側向力分配規律代入模型，同時也考慮其它類型的分配規律代入到車輛模型，通過對比其軌跡，進一步驗證了計算的縱、側向力分配規律的正確性。

（3）本文中在進行基于Carsim和Labview硬件在環試驗驗證理想縱、側向力分配規律時，采用一種基于有限元的路徑分割方法和穩態預測動態校正理論的路徑跟蹤算法，通過硬件在環試驗驗證了在此縱、側向力分配規律下，車輛的輪胎力得到了充分利用，車輛的實際橫擺角速度在理想橫擺角速度附近。最后通過實車試驗進一步驗證了所計算的縱、側向力分配規律的有效性。