水平分層土層系統等效阻尼比的 簡化計算方法1

殷 琳 樓夢麟 康 帥

1）寧波工程學院，建筑與交通工程學院，浙江寧波 315000

2）寧波工程學院，浙江省土木工程工業化建造工程技術研究中心，浙江寧波 315000

3）同濟大學，土木工程學院，上海 200092

4）河南大學，土木工程學院，河南開封 475001

前言

土層地震反應分析是工程場地地震安全性評價和區域地震區劃中的重要工作環節（上海市地震局等，2004；中華人民共和國國家質量監督檢驗檢疫總局等，2006）。在土層地震反應分析中，關于水平均勻土層的研究最為深入（邢浩潔，2017），建立了相關問題的解析解（吳世明，2000；謝定義，2011），如水平均勻土層的水平和豎向線性地震反應的解析解。在實際工程中，土層往往是水平分層的，若要應用水平均勻土層地震反應解析解的理論計算公式，必須把水平分層土層等效為水平均勻土層，其中土層系統的等效阻尼比是需要獲取的1個等效參數。此外，在強震作用下土層介質處于非線性工作狀態，其非線性地震反應分析一般有3種方法，即頻域內的等效線性化計算方法、時域內的等效線性化計算方法和時域內的真非線性計算方法（Idriss等，1968；欒茂田等，1992，2003）。而在時域內進行土層地震反應計算時，無論是線性問題還是非線性問題，一般應用有限元法并采用基于振型阻尼比的瑞利比例阻尼矩陣的形式，按各自土介質阻尼比形成阻尼子矩陣，然后組裝成土層系統的總阻尼矩陣無疑是合理的數值建模方法（Idriss等，1973）。在實際應用中，更為簡便、快速的途徑是在土層整體層面上，形成系統的瑞利比例阻尼矩陣，為此需首先獲得水平均勻土層系統的等效阻尼比。

樁-土動力相互作用是工程結構抗震設計理論研究中的1個重要方面，基于單樁阻抗函數的群樁基礎模型已在工程結構抗震計算和設計中得到廣泛應用，而單樁阻抗函數的解析解是建立在土層為水平均勻的假定之上。已有研究（樓夢麟等，2012）表明：把水平分層土層等效為水平均勻土層有助于在工程中應用水平均勻土層的研究成果，各國在建筑抗震規范中都有相應的規定（中華人民共和國住房和城鄉建設部等，2010）。土層系統等效阻尼比是將水平分層土層等效為水平均勻土層過程中應該考慮的重要力學參數。

本文重點探討水平分層土層系統的等效阻尼比的計算方法。

1 水平變參數土層等效阻尼比的計算方法

眾所周知，土層介質的動力物理特性參數隨埋深變化，即便是單一介質的水平土層，也不是水平均勻土層，其動力參數也沿土層深度有所變化，稱為水平單層變參數土層。同樣，任何水平分層土層也都是變參數水平土層。本文把水平單層變參數土層、水平分層均勻土層和水平分層變參數土層簡稱為水平變參數土層。下面先討論一般意義下水平變參數土層系統的等效阻尼比的近似計算方法。

設水平變參數土層總厚度為H，共有n層土，第i層土的中心位置距下臥基巖面的距離 為zi，該位置處的土介質的阻尼比為λ(zi)，則該水平變參數土層的等效阻尼比λeff為：

式中，f(z)為加權函數。

加權函數f(z)的形式可有不同選擇，本文選擇5種加權函數：①假設各層土的阻尼比對等效阻尼比的貢獻相同，即權函數f(z)是等權函數；②假設各層土的阻尼比對等效阻尼比的貢獻隨其所處深度從基巖至地表呈正弦函數變化，即權函數f(z)取為水平均勻土層第一階振 型的位移分布函數，即為正弦函數；③假設各層土的阻尼比對等效阻尼比的貢獻隨其所處深 度從基巖至地表成余弦函數變化，即權函數f(z)取為水平均勻土層第一階振型的剪切應變分 布函數，即第一階振型的位移分布函數的導數，為余弦函數；④加權函數f(z)為倒三角形分布，可看作第2種加權函數的簡單近似；⑤加權函數f(z)為三角形分布，可看作第3種加權 函數的簡單近似。上述5種加權函數如圖1所示。

圖1 加權函數分布圖 Fig.1 Plots of weighting function

當5種加權函數的最大值為1時，由式（1）可得到相應的變參數土層等效阻尼比的表達式。

（1）當加權函數f(z) = 1時，

式中，z為土層上任意一點到基巖面的距離，H為土層總厚度（下同）。

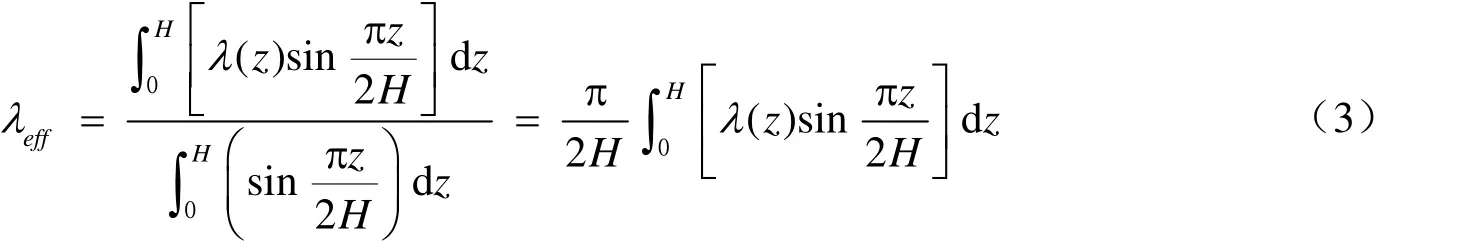
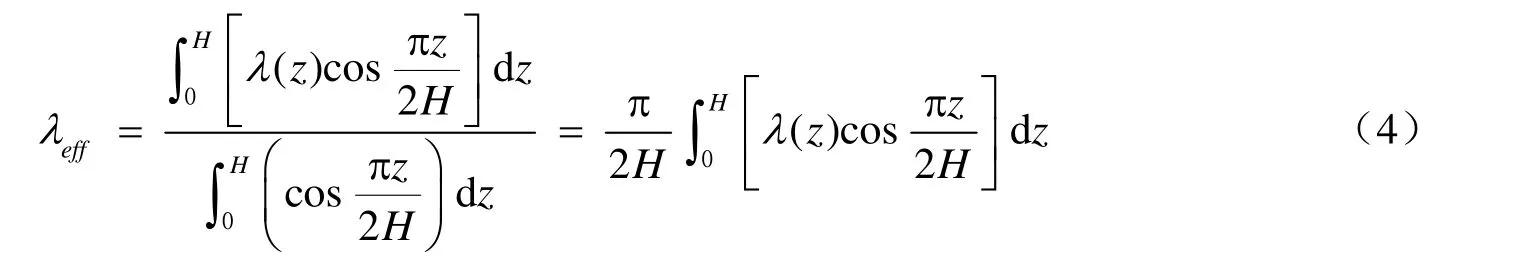
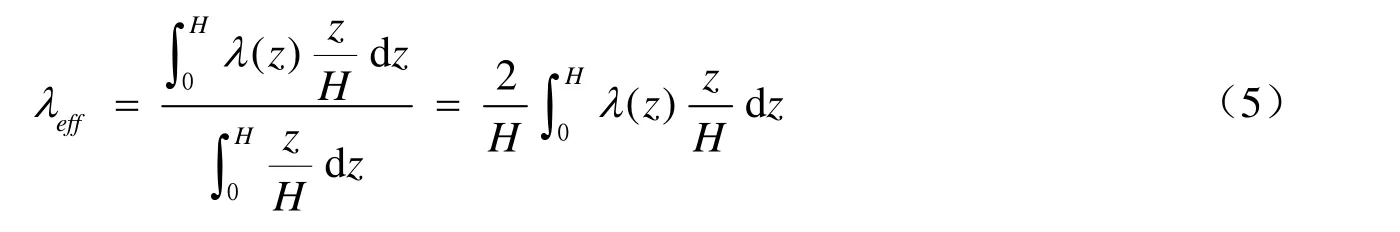
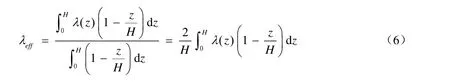
2 計算水平分層均勻土層等效阻尼比的加權比例因子

圖2所示的水平分層土層可視為水平變參數土層的1個特例，其土層介質力學特性參數的分布沿豎向埋深呈階躍函數，即每層土的阻尼比恒定，不隨埋深變化。為表述方便，定義iλ為第i層土介質的阻尼比，Zi和Zi-1分別為第i層土層上、下界面的Z坐標值，hi為第i層土厚度，iH為第i層土層中心至土表的距離，也即第i層土層中心面的埋深，它們之間的關系為：

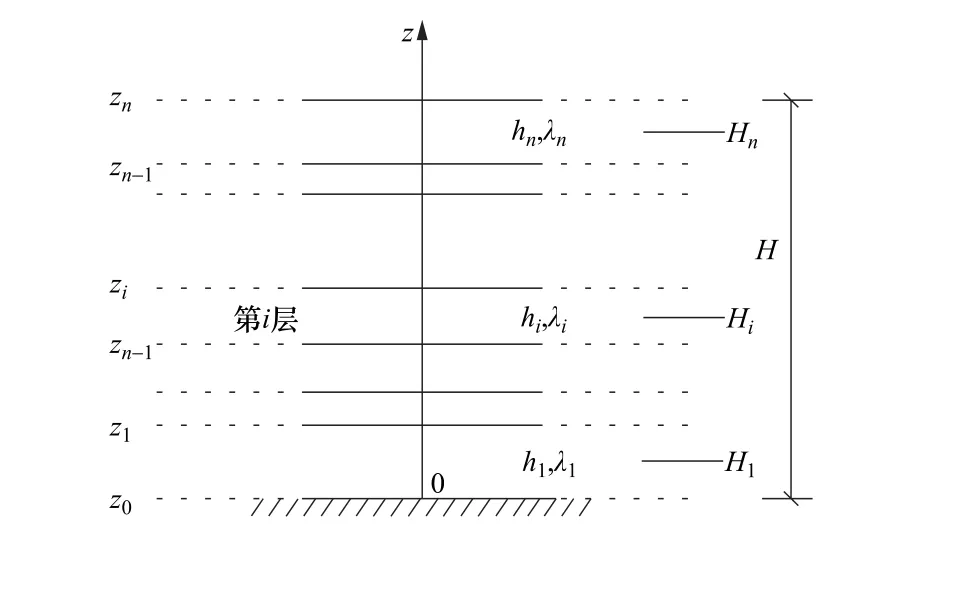
圖2 分層土層及相關參數示意 Fig.2 Illustration of layered soils and corresponding parameters

當各土層的阻尼比為常數時，由式（2）—（6）可分別得到：

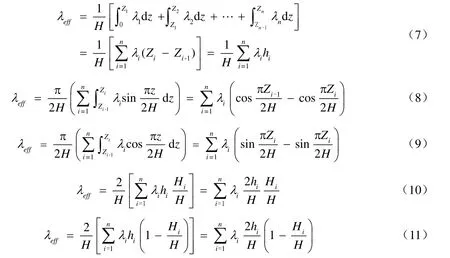
上述基于水平變參數土層加權函數并通過積分計算獲得等效阻尼比的方法（式（2）—（6）），稱為方法a。如將式（7）—（11）寫成如下形式：

則稱Dia為第i層土的阻尼比加權比例因子，其值介于0和1之間。對應式（7）—（11）的加 權比例因子分別標記為：

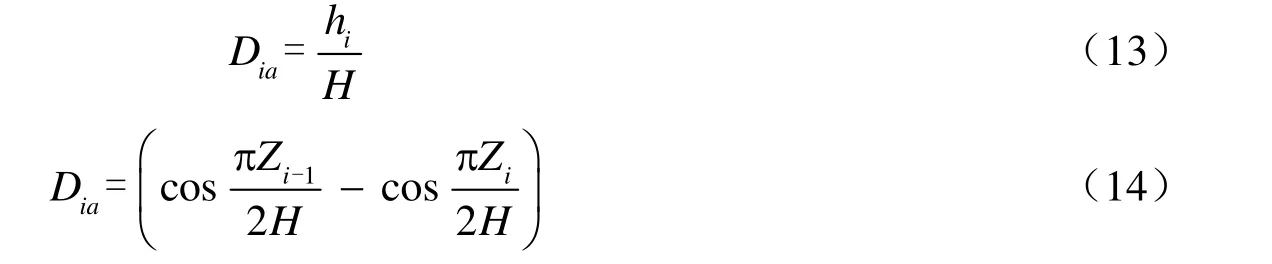
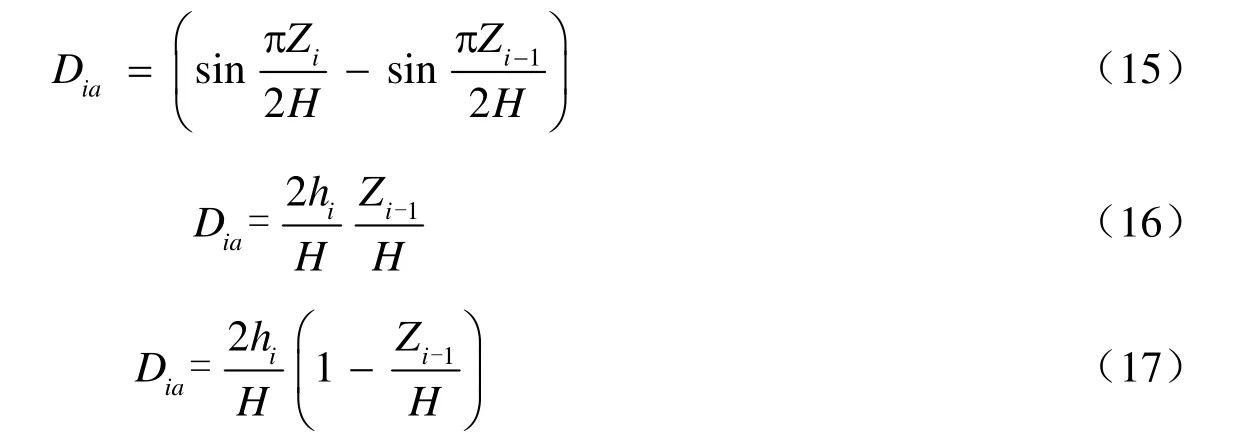
同時，考慮到每層土的阻尼比是恒定不變的，每層土層可取相同的加權系數fi來計算等效阻尼比，將各層直接指定加權系數的方法記為方法b，此時水平分層均勻土層的等效阻尼比為：

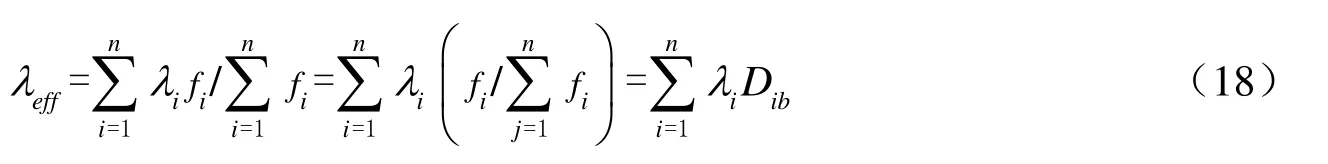
式中，第i層的加權比例因子Dib為：

本文選用6種加權系數，分別為：①fi=hi，即取第i層的層厚為該層的加權系數；即取第i層中心面處的均勻土層第1階振型位移函數值為該層的加權系數；即取第i層中心面處的均勻土層第1階振型的應變函數值為該層的加權系數；即取第i層中心面處的埋深為該層的加權系數；即取第i層中心面處的高程坐標為該層的加權系數；此時考慮了層厚和埋深的雙重影響。樓夢麟 等（2012）對第1、4和6種加權系數的取值方法進行了應用和比較，在上述6種加權函數假定下，各層土層的加權比例因子分別為：

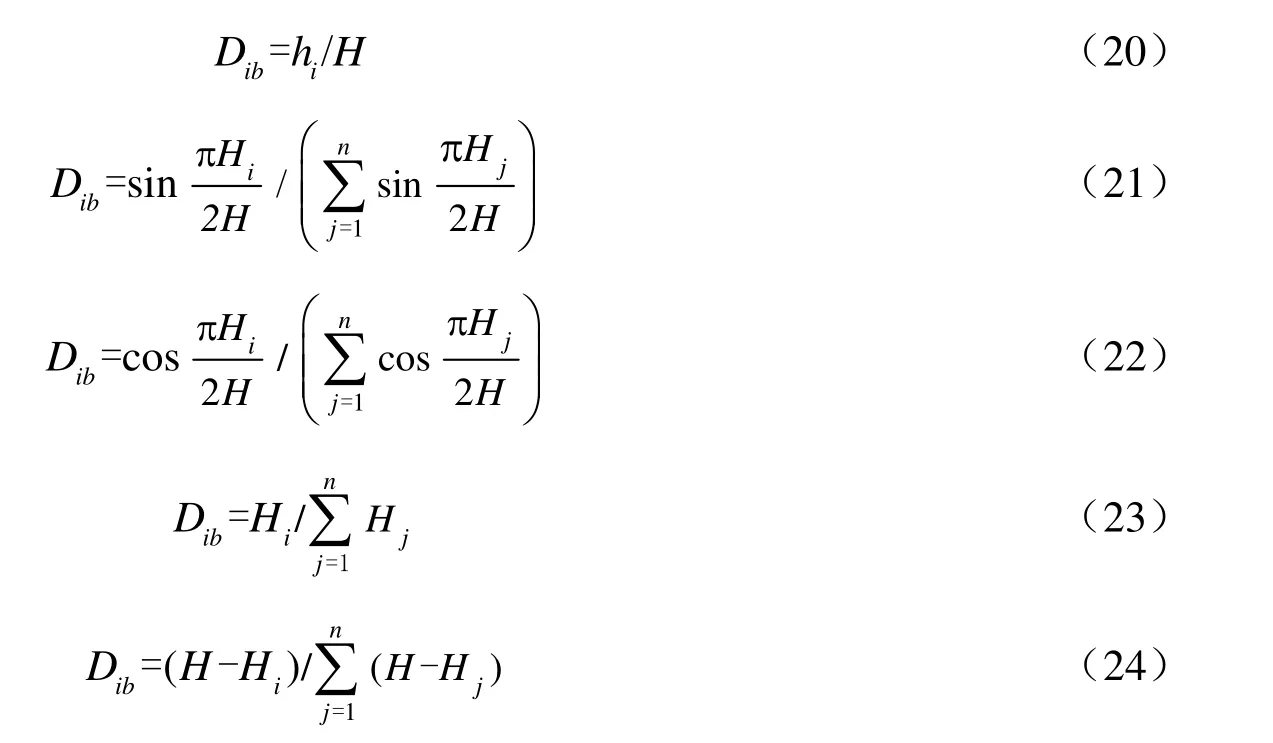
比較式（13）和式（20）可知，對于水平分層均勻的土層而言，以層厚為加權系數的實質是采用了等權加權函數；此外，考察式（25）中的分母，由于zn=H，z0=0，其分母可以進一步簡化為：將此結果代入式（25），可得與式（16）中的Dia相同， 證明了采用三角形分布作為加權函數考慮了層厚和深度的雙重影響。

由基于分布加權函數的方法a和直接指定各層加權系數的方法b共形成了11種加權比例因子，實際共提出了9種不同加權比例因子的取值方法，分別表為a1、a2、a3、a4、a5和b2、b3、b4、b5。下文通過算例來討論不同加權比例因子對土層地震反應計算結果的影響。

3 算例分析

基于土介質耗能機理的試驗研究成果，在土動力學原理中常采用滯回阻尼模型，其數學描述是復剛度形式。為此，本文在頻域內計算土層的線性地震反應，也可避免時域內的比例阻尼矩陣建模存在問題（樓夢麟，2016）。在假定土介質為線性的條件下，計算了2個水平分層土層的地震反應，通過分析土層地表的地震加速度與位移反應峰值的計算精度來討論文中所建議的不同加權方法的合理性。采用線性假定可獲取土層地震反應的準確解，用于評價近似解的計算精度，所得結論可以推廣到水平分層土層的非線性地震反應的計算問題。

3.1 算例1

水平分層土層的總厚度為100m，土層分為10層，每層10m，分層情況如圖3所示。各土層物理參數均為：密度2000kg/m3，彈性模量391MPa，泊松比0.35，換算剪切波速為269m/s。

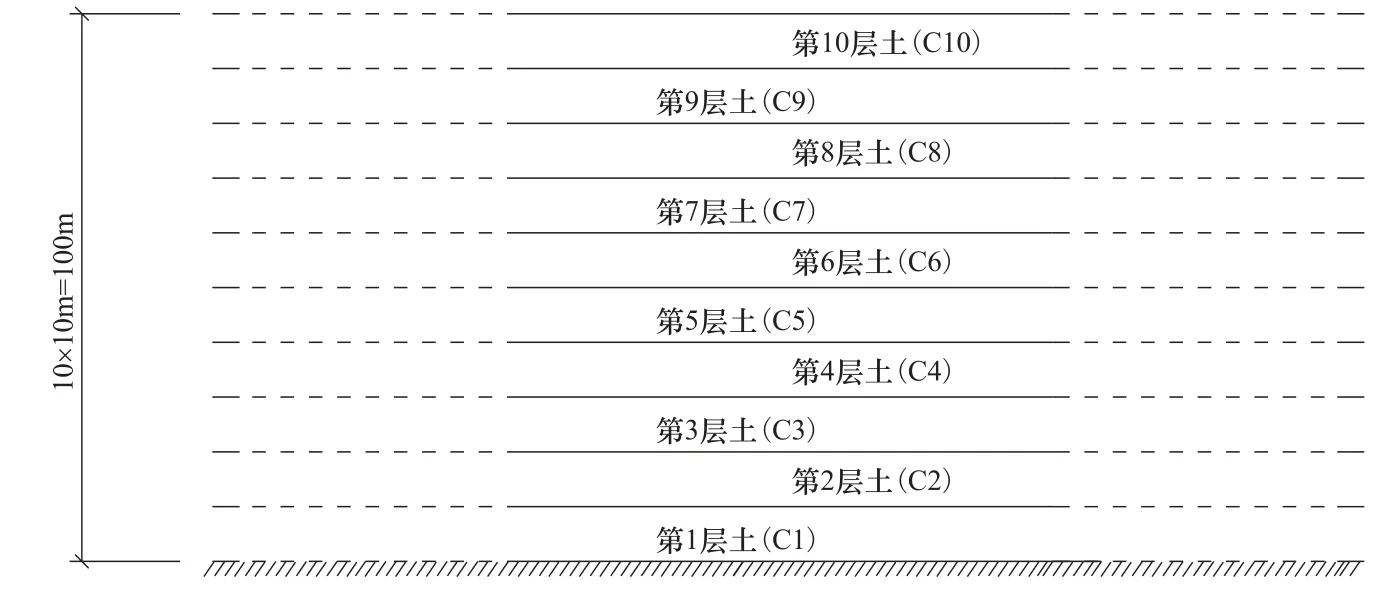
圖3 分層土層場地 Fig.3 Layered soil sites

對于水平地震作用下水平分層土層的地震反應，可采用單列平面應變有限元方法來計算（鄔都等，2008）。為確保頻率低于20Hz的地震波分量均能傳到地表而不被濾波，有限元網格的豎向尺寸應滿足最小尺寸要求，即最大豎向單元尺度lmax應不大于λ/8，其中λ為對應于最高激振頻率的正弦波在此土層中傳播的波長，一般情況下基巖地震波的最高激振頻率取為20Hz。由土層模型的物理參數知，激振頻率為20Hz的正弦波在此土層中傳播的波長為：

在本算例中，網格豎向尺寸取l=1m，可滿足上述有限單元豎向尺寸的要求。

該平面應變有限元模型底部結點自由度全約束，兩側邊界上的結點僅約束豎向自由度，成為側移邊界。

將圖3中各層土介質的阻尼比設為不同值后，形成S1、S2和S3共3種水平分層土層模型，3種模型各層土阻尼比的設置值列見表1。在各層土厚度hi相等的情況下，可以證明 式（16）、（17）中的Dia分別與式（23）、（24）中的Dib相同，由于篇幅限制，在此不再贅述。

表1同時給出了7種計算方法下的等效阻尼比。

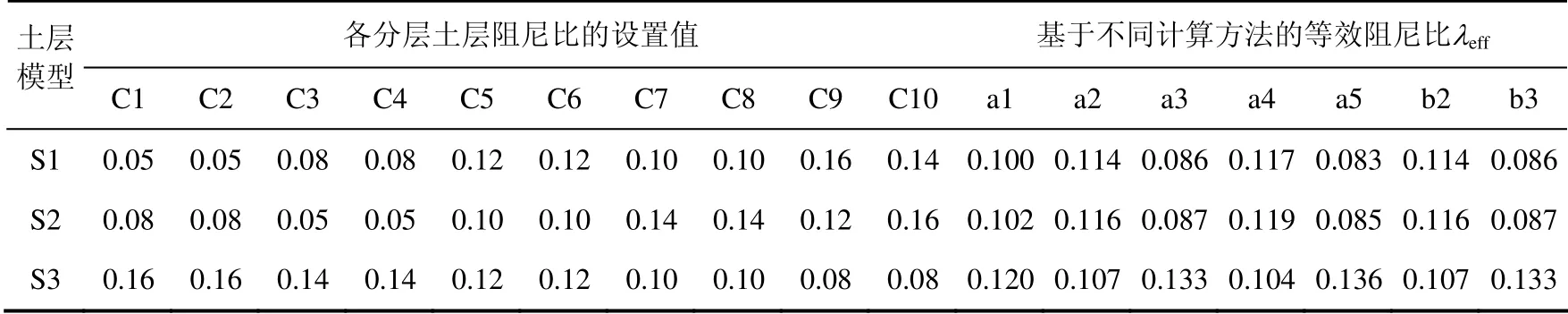
表1 不同土層模型的阻尼比分布及基于不同計算方法的等效阻尼比 Table1 Distribution of damping ratios of the soil modals and calculated damping ratios

表1中的數據表明，方法b2、b3所得的等效阻尼比與方法a2、a3所得值相等，方法a2和a4所得的等效阻尼比相近，方法a3和a5所得的等效阻尼比相近。因此，下文只驗算方法a1—a5所得的等效阻尼比對土層地震反應的影響。

對于每一個土層模型，首先在頻域中計算分層土層在原始阻尼比時的土層地表的地震反應，將其作為比較的基準值，然后在頻域內分別應用方法a1—a5所得的等效阻尼比計算同一 土層的地震反應，并與基準值比較，以相對誤差水平ei判斷不同等效阻尼比時的計算精度， 相對誤差水平的計算公式為：

其中，A0表示土層地震反應峰值的基準值，Ai表示應用等效阻尼比計算所得的同一土層 地震反應峰值。

土層下臥基巖面上輸入的地震加速度時程分別為實測得到的4條地震加速度時程，分別簡稱為El-Centro波、Taft波，Kobe波，汶川基巖波，此外還選用了上海地區某工程場地地震安評所得的50年10%概率下的人工基巖波。在計算中，將5條地震加速度時程的幅值均調整為1.00m/s2，相應的時程曲線及其反應譜如圖4所示。

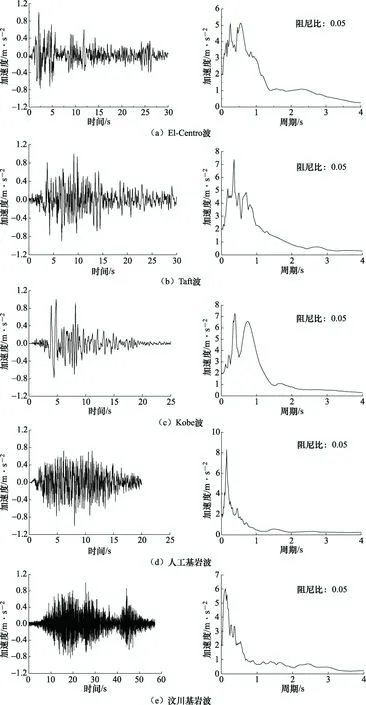
圖4 地震波時程曲線及反應譜 Fig.4 Time history and response spectrum diagram of seismic wave

表2給出了各種土層模型下的土層地表絕對加速度與相對位移反應峰值，表3給出了對應的計算相對誤差。

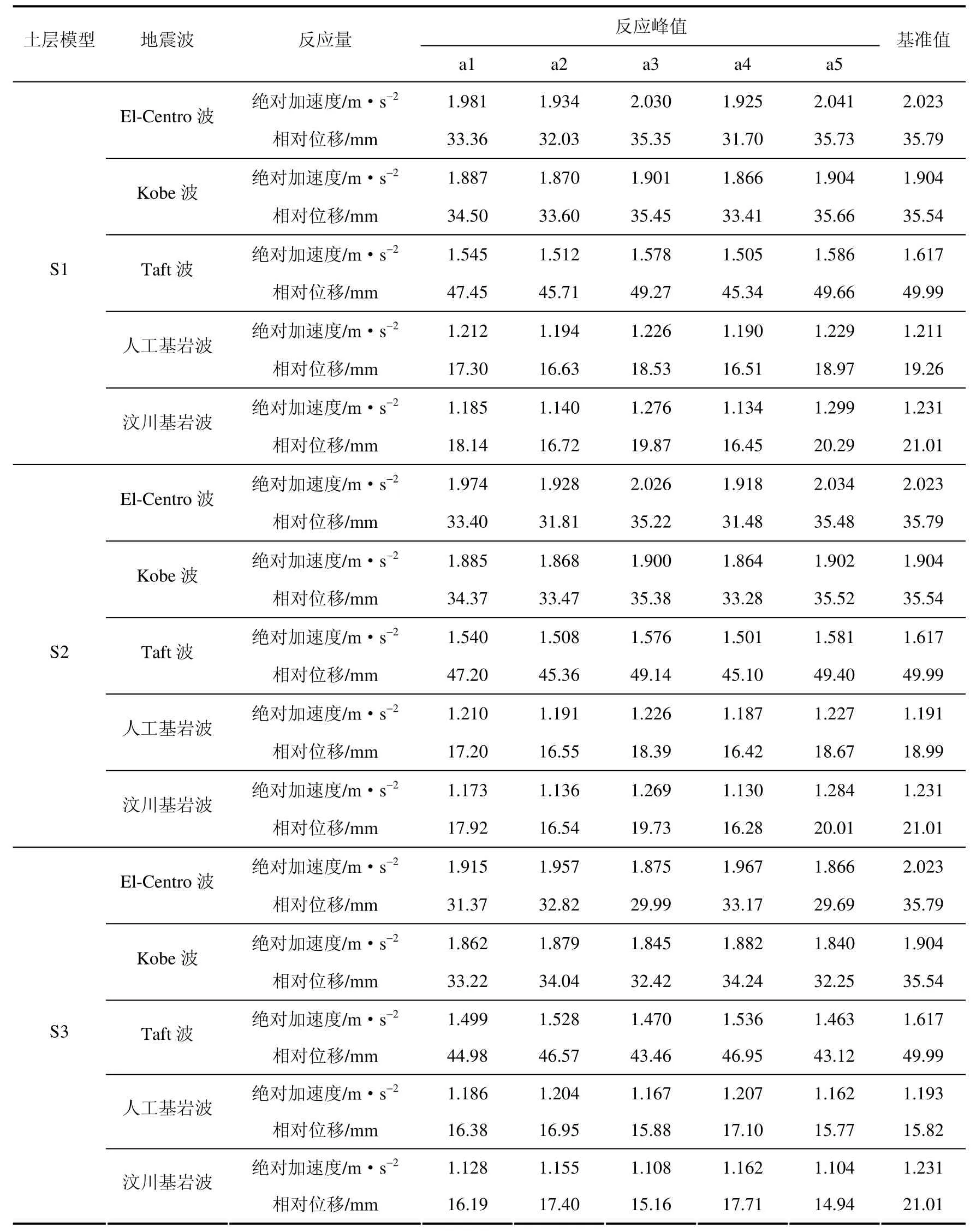
表2 不同土層模型地表的地震反應峰值 Table2 Peak seismic response of different soil layer models

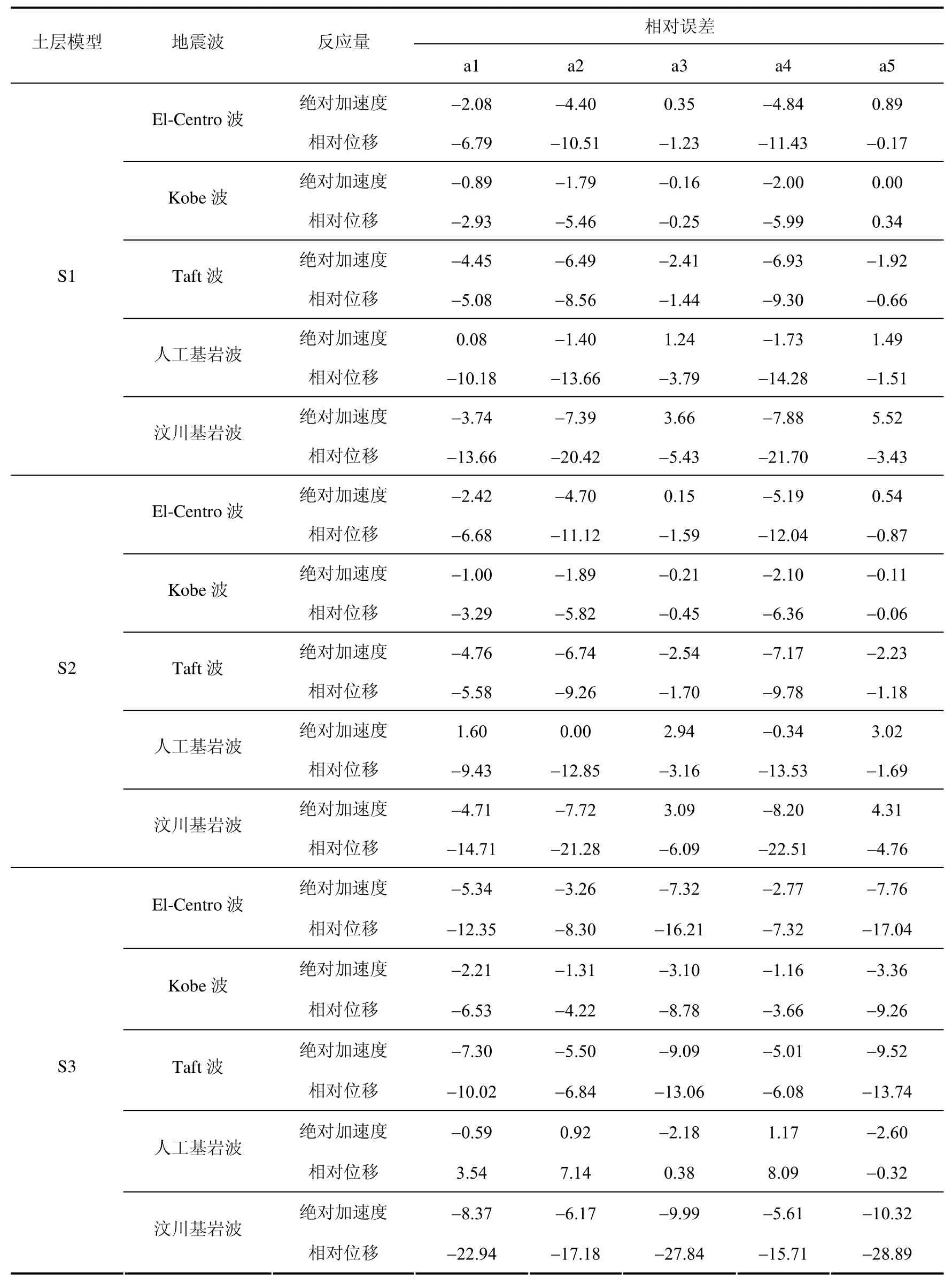
表3 不同土層模型地表的地震反應峰值的相對誤差（單位：%） Table3 Relative errors of peak seismic response of different soil layer models (unit:%)

從表3的數據可以看出，不同的等效方法會產生不同的誤差水平，從總體來看，在等厚度分層土層的條件下，近似估算方法a3和a5所產生的誤差基本相同，同樣，近似估算方法a2和a4所產生的誤差基本相同，即用直線代替正弦或余弦曲線來表示加權函數所得的等效阻尼比和產生的計算誤差水平基本相同。對于土層模型S1和S2，近似估算方法a3和a5所產生的誤差要小一些，且普遍小于5%。而對于土層模型S3，近似估算方法a2和a4所產生的誤差要小一些，多數情況下小于5%，只有汶川地震波的誤差大一些，主要是由于該地震波的廣譜性造成的。進一步比較表明，土層模型S1和S2的阻尼比由地表到基巖呈減小趨勢，宜采用正三角形分布的加權函數，而土層模型S3的阻尼比由地表到基巖呈增加趨勢，宜采用倒三角形分布的加權函數。

3.2 算例2

以蘇通大橋5號橋塔基礎處的工程場地為實際算例，進一步討論不同等效阻尼比近似估算方法的合理性。該工程場地可近似視為水平分層土層，共劃分為11層，相關計算參數如表4所示。

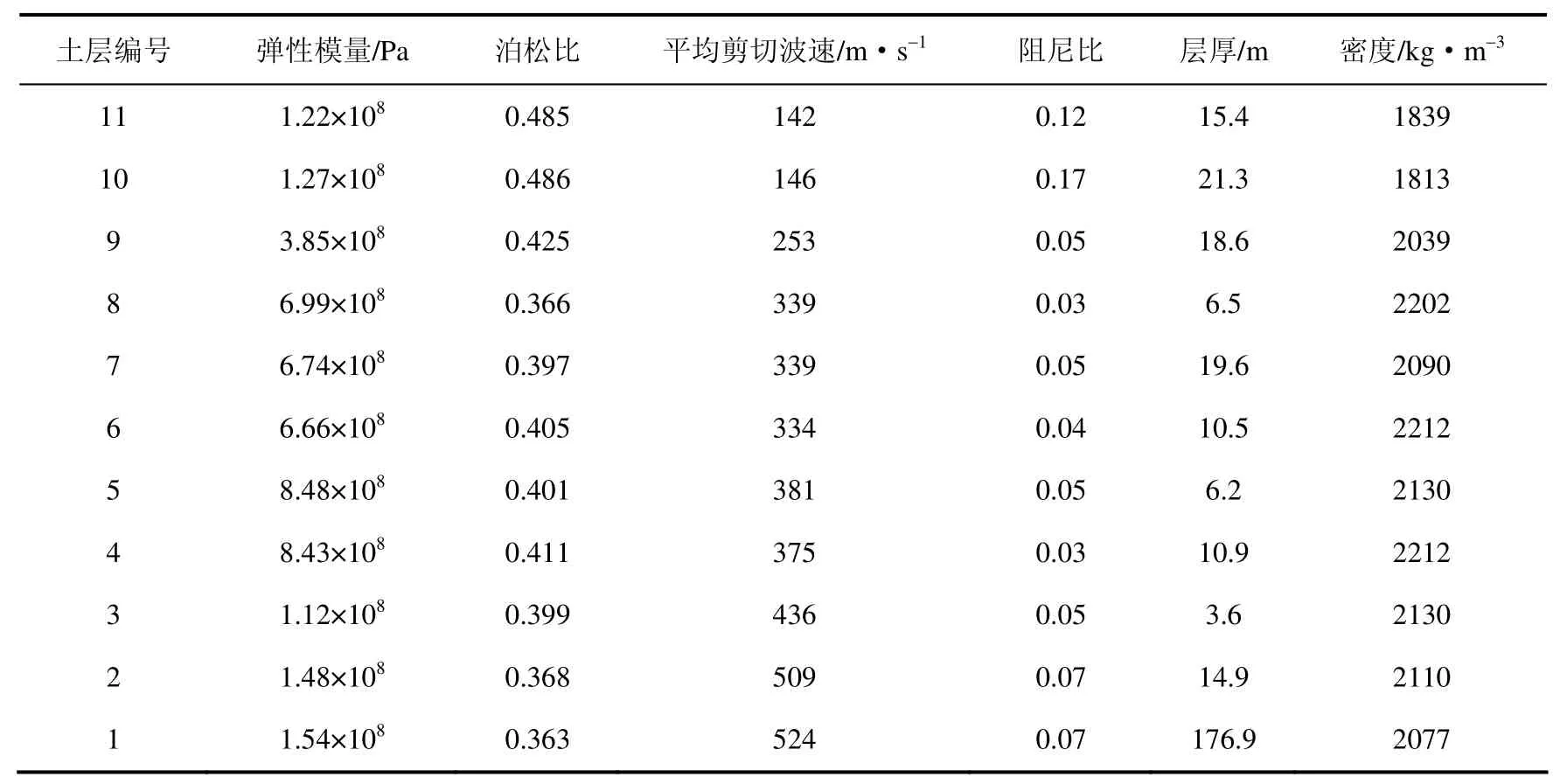
表4 工程場地土層模型基本參數 Table4 Parameter of soil sites

根據土的分層情況及相關參數，可得到不同近似估算方法所得的土層等效阻尼比，如表5所示。從表中數據可以看出，采用方法a3、a5和b2所得的等效阻尼比相等，采用方法a2和a4所得的等效阻尼比相近，采用方法b3和b5所得的等效阻尼比相近。該場地地震反應有限元模型的建立與求解方法與算例1相同，計算結果見表6和表7。

表5 土層模型各方法計算出的等效阻尼比 Table5 Equivalent damping ratios of soil site by different method

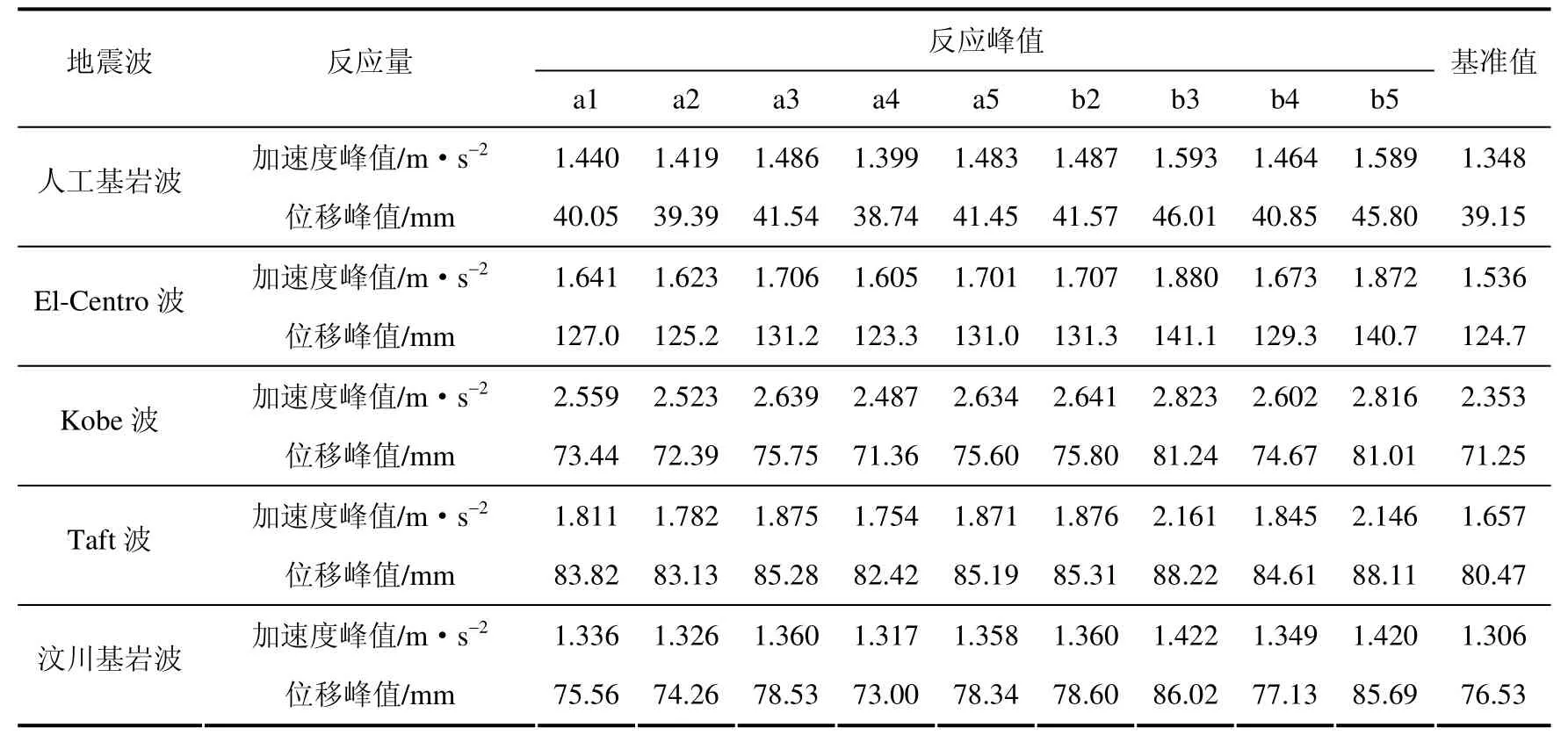
表6 土層地震反應峰值 Table6 Peak value of seismic responses of soil layer

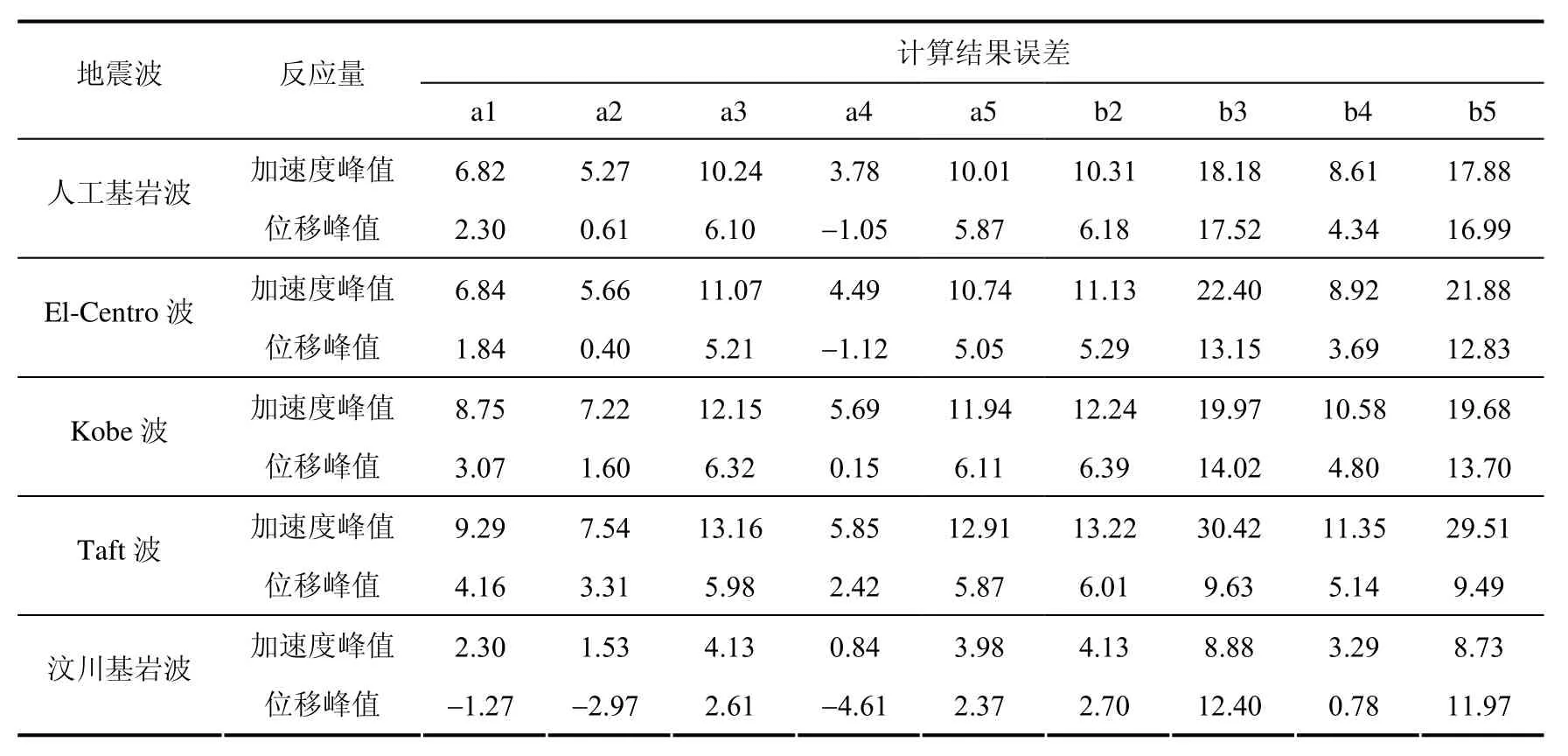
表7 地震反應計算結果誤差（單位：%） Table7 Errors of seismic response calculation (unit:%)

從表7的數據可以看出，近似估算方法a2和a4產生的誤差要小一些，多數情況下小于5%。由于最下層土層厚達176.9m，超過土層厚度304.4m的一半，盡管地表2層土層的阻尼比較大，但該場地土層的各層土層阻尼比變化總的趨勢是由地表向基巖增加，與前一算例中S3土層相似，也有相似的結論。在這種情況下，宜采用近似估算方法a2和a4，且a2和a4的誤差水平相當。

此外，從表7還可以看出，與近似估算方法a2和a4相對應的近似估算方法b2和b4，其計算誤差要大的多，表明層厚差別較大時，宜采用基于分布加權函數的方法a，而不采用直接指定各層加權系數的方法b。

4 結語

（1）在進行水平分層土層地震反應分析時，若所選擇的等效阻尼比計算方法不恰當，將導致計算所得的地震反應出現較大的誤差，在本文的算例中，最大可達30%。

（2）在水平分層土層中，若各層土阻尼比由地表到基巖呈增強趨勢，則采用a5方法（即正三角形分布）計算等效阻尼比較合理；若各層土阻尼比由地表到基巖呈減小趨勢，則采用a4方法（即倒三角形分布）來計算等效阻尼比較合理。

（3）總體上，采用基于分布加權函數的方法更為合理，適用性更為廣泛。