橢圓形柱體地震動(dòng)水壓力的簡(jiǎn)化分析方法1

王丕光 黃義銘 趙 密 杜修力 張麗華

1）清華大學(xué)土木工程系，北京 100084

2）北京工業(yè)大學(xué)城市與工程安全減災(zāi)教育部重點(diǎn)實(shí)驗(yàn)室，北京 100124

3）華北科技學(xué)院，北京 101601

引言

近年來(lái)，隨著世界經(jīng)濟(jì)的發(fā)展，中國(guó)近海結(jié)構(gòu)的研究得到了快速發(fā)展，如跨海橋梁、海上風(fēng)電、人工島和石油平臺(tái)等。然而，中國(guó)福建、廣東沿海和中國(guó)臺(tái)灣等地區(qū)的近海結(jié)構(gòu)面臨著地震作用的威脅。在地震作用下，橋梁與周?chē)w的相互作用會(huì)對(duì)橋墩產(chǎn)生動(dòng)水壓力。地震作用下水體與結(jié)構(gòu)的動(dòng)力相互作用會(huì)對(duì)結(jié)構(gòu)產(chǎn)生附加動(dòng)水壓力，其不僅會(huì)改變結(jié)構(gòu)的動(dòng)力特性，還會(huì)對(duì)水中結(jié)構(gòu)的動(dòng)力反應(yīng)產(chǎn)生較大影響（Liaw等，1974；Han等，1996；黃信等，2011a；江輝等，2014）。因此，充分認(rèn)識(shí)和研究地震激勵(lì)下近海結(jié)構(gòu)的動(dòng)水壓力，對(duì)于近海結(jié)構(gòu)的抗震設(shè)計(jì)具有重要意義。

在實(shí)際近海工程中存在各種截面形式的墩柱結(jié)構(gòu)，如圓形和橢圓形等。目前，國(guó)內(nèi)外學(xué)者對(duì)圓柱結(jié)構(gòu)地震動(dòng)水壓力的研究已取得大量的研究成果。Liaw等（1974）基于輻射波浪理論推導(dǎo)了圓柱結(jié)構(gòu)的動(dòng)水壓力公式，結(jié)果表明，對(duì)于細(xì)長(zhǎng)結(jié)構(gòu)可以忽略水體壓縮性的影響；表面波僅在低頻時(shí)對(duì)動(dòng)水壓力的影響比較明顯。忽略水體壓縮性和表面波時(shí)，該動(dòng)水壓力可視為部分水體質(zhì)量與結(jié)構(gòu)加速度的乘積，這部分水體稱(chēng)為“附加質(zhì)量”。Williams（1986）采用邊界積分方法研究了地震作用下水中圓柱結(jié)構(gòu)的動(dòng)力反應(yīng)。Tanaka等（1988）分析了水平地震作用下彈性圓柱體動(dòng)水壓力的附加質(zhì)量系數(shù)和阻尼系數(shù)。Han等（1996）提出了計(jì)算水中圓柱結(jié)構(gòu)自振頻率的簡(jiǎn)化公式。賴(lài)偉等（2004）提出了一種圓形橋墩上地震動(dòng)水壓力的半解析半數(shù)值方法。黃信等（2011b，2012）討論了水體壓縮性、表面波和水底吸收邊界對(duì)圓形橋墩地震動(dòng)水壓力的影響。杜修力等（2012）、Du等（2014）提出了可壓縮水體條件下圓柱結(jié)構(gòu)地震動(dòng)水壓力的時(shí)域算法和時(shí)域簡(jiǎn)化公式。Goyal等（1989）、Li等（2013）和Jiang等（2017）提出了圓柱形橋墩上地震動(dòng)水壓力的附加質(zhì)量簡(jiǎn)化計(jì)算公式。另外，Liao（1985）研究了水中多個(gè)圓柱結(jié)構(gòu)的動(dòng)力相互作用；Sun等（1991）研究了軸對(duì)稱(chēng)結(jié)構(gòu)的地震動(dòng)水壓力；Avilés等（2001）討論了海底吸收條件對(duì)軸對(duì)稱(chēng)結(jié)構(gòu)地震動(dòng)水壓力的影響；Wei等（2015）提出了水中軸對(duì)稱(chēng)結(jié)構(gòu)的地震設(shè)計(jì)和分析的簡(jiǎn)化方法。

上述分析表明，地震作用下圓柱結(jié)構(gòu)與水體的動(dòng)力相互作用問(wèn)題已取得了可供實(shí)際應(yīng)用的研究成果，但對(duì)橢圓柱體結(jié)構(gòu)動(dòng)水壓力方面仍鮮有研究。本文基于橢圓坐標(biāo)系，根據(jù)線性輻射波浪理論，利用分離變量法推導(dǎo)了橢圓柱體結(jié)構(gòu)動(dòng)水壓力的解析解，并采用有限元方法建立了地震作用下水體與橢圓柱體結(jié)構(gòu)動(dòng)力相互作用的簡(jiǎn)化分析方法。

1 橢圓形柱體動(dòng)水壓力求解

地震作用下橢圓柱體結(jié)構(gòu)與水體動(dòng)力相互作用的分析模型如圖1所示，a和b分別表示橢圓外徑的半長(zhǎng)軸和半短軸，a1和b1分別表示橢圓內(nèi)徑的半長(zhǎng)軸和半短軸，h為水深，H為柱體高度。直角坐標(biāo)系下，z軸沿柱體軸線向上，坐標(biāo)原點(diǎn)位于柱體底部；地基為剛性，地面運(yùn)動(dòng)加速度為。水體假定為無(wú)旋、無(wú)粘、可壓縮的小擾動(dòng)流體，并忽略表面重力波的影響。

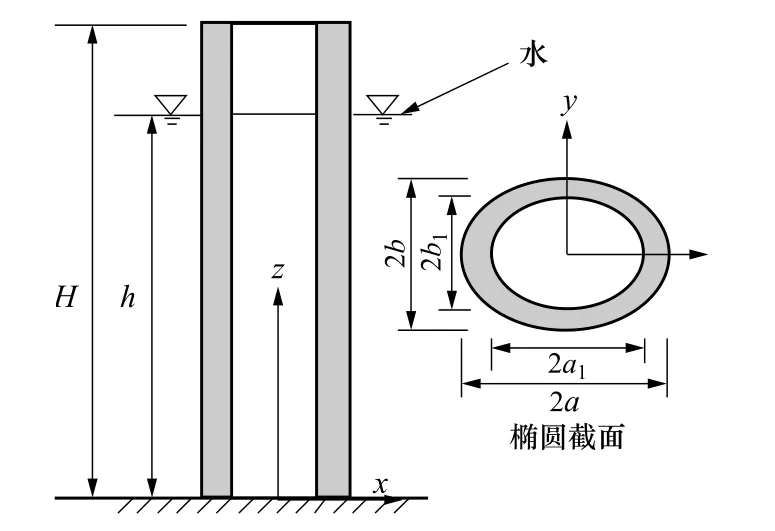
圖1 橢圓柱體與水體相互作用分析模型 Fig.1 Analytical model of the interactiin of elliptic cylinder and water

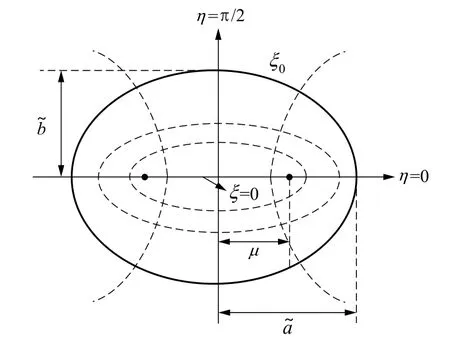
圖2 橢圓坐標(biāo)系 Fig.2 Elliptical cylindrical coordinate

1.1 控制方程和邊界條件

由于柱體截面呈橢圓形，故在橢圓坐標(biāo)系下求解橢圓柱體的地震動(dòng)水壓力。橢圓坐標(biāo)系如圖2所示。直角坐標(biāo)系與橢圓坐標(biāo)系直接的變化關(guān)系為：

在橢圓柱坐標(biāo)系下，以動(dòng)水壓力p表示的流體控制方程為（Bhatta，2005）：

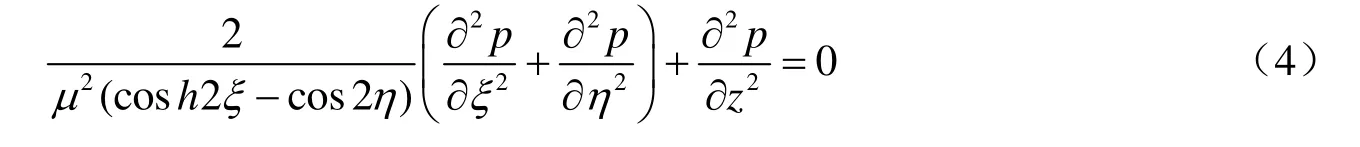
水體底部、靜水表面和無(wú)窮遠(yuǎn)邊界條件為：

地震動(dòng)沿長(zhǎng)軸方向時(shí)，η=0和η=0.5π面的對(duì)稱(chēng)邊界條件為：

地震動(dòng)沿短軸方向時(shí)，η=0和η=0.5π面的對(duì)稱(chēng)邊界條件為：

地震動(dòng)沿長(zhǎng)軸和短軸方向時(shí)，水體與結(jié)構(gòu)交界面邊界條件分別為：

式中，ρ表示水體密度，表示結(jié)構(gòu)的加速度。

1.2 分離變量求解

在橢圓柱坐標(biāo)系下，p(ξ,η,z)可分離變量為：

將式（12）代入式（4）整理得到3個(gè)解耦的方程：

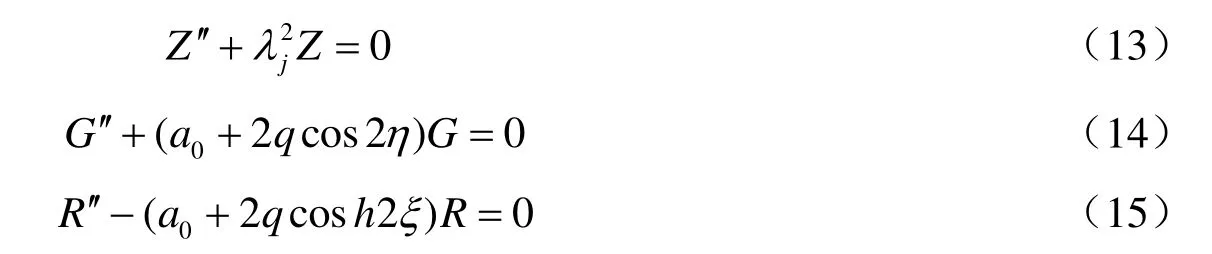
式中，λj和a0是分離變量常數(shù)，q=μ2λ2j/4為一無(wú)量綱參數(shù)。

由方程（13）和邊界條件式（5）、（6）可得：

式中，dj為待定系數(shù)，λj= (2j- 1)π /2h，j=1，2，…。通過(guò)正交歸一化可得

方程（14）為修正的角向馬蒂厄方程（熊天信，2014），其解為第一類(lèi)角向馬蒂厄函數(shù)cen(η,-q)和sen(η,-q)，即：

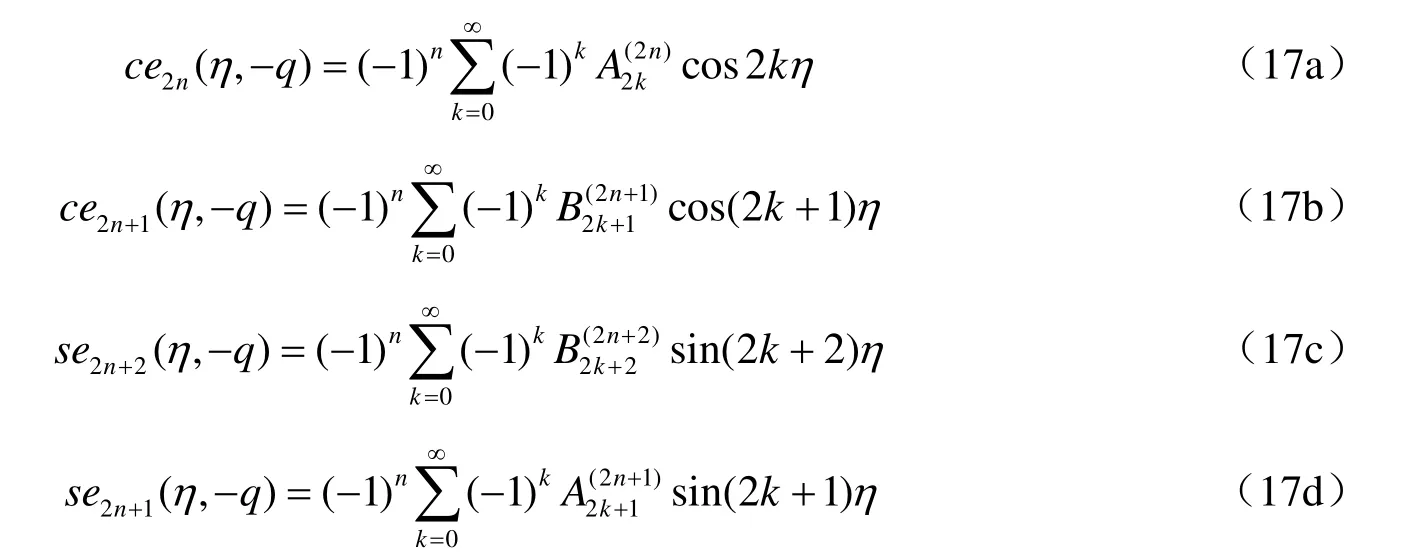
函數(shù)cen(η,q)和sen(η,q)的歸一化正交關(guān)系為：

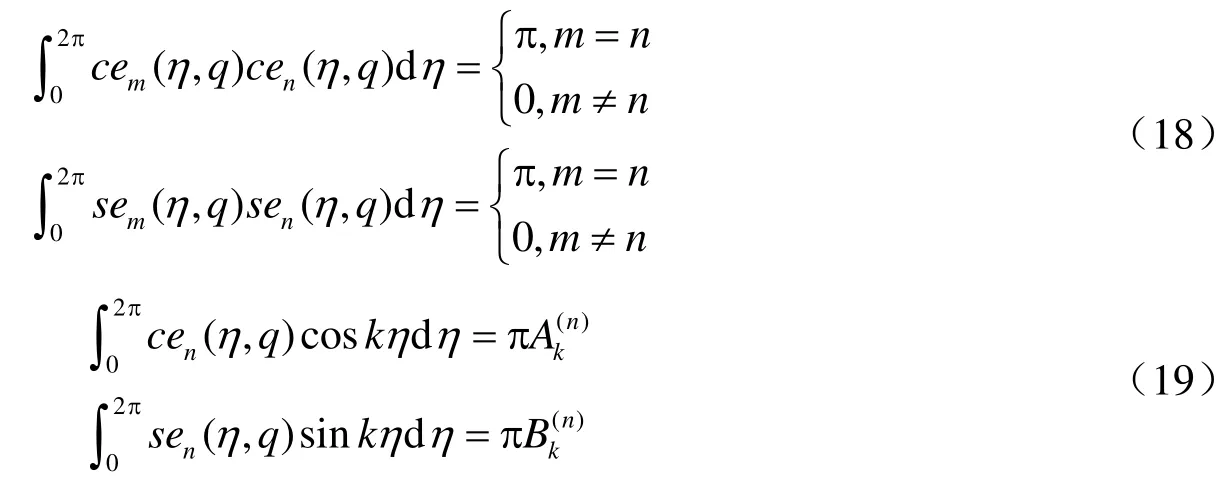
方程（15）為修正的徑向馬蒂厄方程（熊天信，2014）。整數(shù)階徑向馬蒂厄方程的完全解為：

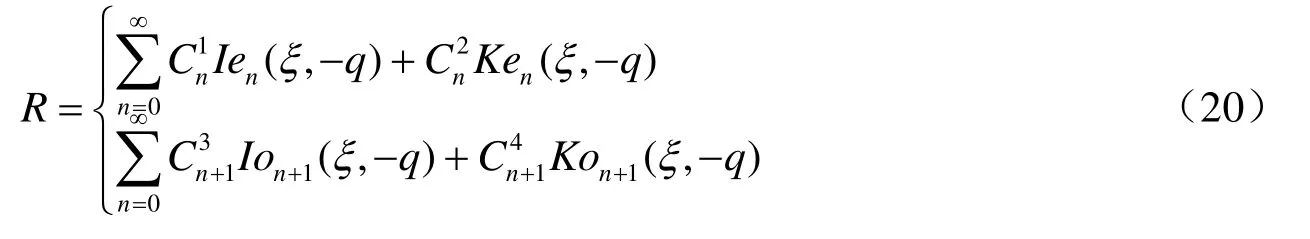
式中，是任意常數(shù)；函數(shù)Ien(ξ,-q)和Ion(ξ,-q)稱(chēng)為第一類(lèi)變形貝塞爾型徑向馬蒂厄函數(shù)，是單調(diào)遞增函數(shù)；函數(shù)Ken(ξ,-q)和Kon(ξ,-q)稱(chēng)為第二類(lèi)變形貝塞爾型徑 向馬蒂厄函數(shù)，是單調(diào)遞減函數(shù)。

1.3 柱體的動(dòng)水壓力

當(dāng)?shù)卣饎?dòng)沿長(zhǎng)軸方向時(shí)，根據(jù)邊界條件式（5）—（8）和（10），并利用式（18）的正交性可得式（12）的解為：

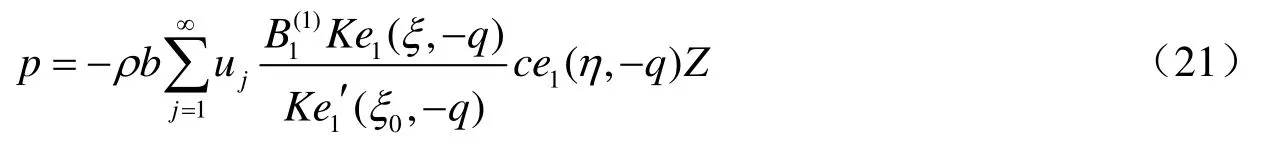
當(dāng)?shù)卣饎?dòng)沿短軸方向時(shí)，根據(jù)邊界條件式（5）—（7）、（9）和（11），并利用式（18）的正交性可得式（12）的解為：

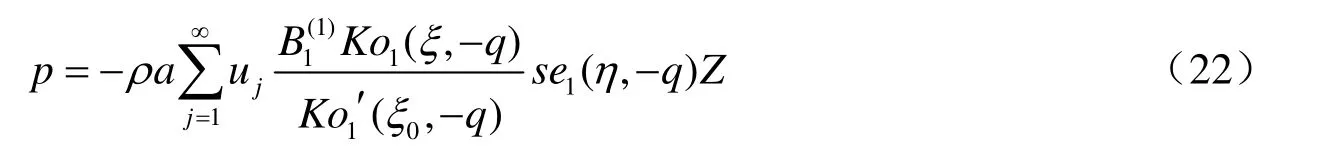
式中，Ko1′ (ξ,-q)為函數(shù)Ko1(ξ,-q)的一階導(dǎo)數(shù)。

地震作用沿長(zhǎng)軸方向時(shí)，橢圓截面柱體表面單位高度上的動(dòng)水力為：

將式（21）代入式（23）整理得：

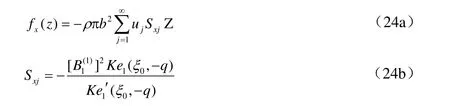
地震作用沿短軸方向時(shí)，橢圓截面柱體表面單位高度上的動(dòng)水力為：

將式（22）代入式（25）整理得：

1.4 方法驗(yàn)證

首先，通過(guò)圓形橋墩動(dòng)水力的解析解（Li等，2013）驗(yàn)證本文提出的橢圓形截面柱體動(dòng)水壓力的解析解。假定結(jié)構(gòu)為剛性，將單位高度動(dòng)水力沿高度積分，可得到橢圓形柱體的均布附加質(zhì)量系數(shù)為：

式中，m0為單位高度水體的附加質(zhì)量，沿長(zhǎng)軸 方向時(shí)m0=ρπb2，沿短軸方向時(shí)m0=ρπa2。 圖3為本文圓柱體附加質(zhì)量系數(shù)的解與圓柱解析解的對(duì)比。由圖3可以看出，本文解與圓柱解析解很好地吻合。

進(jìn)一步通過(guò)Wang等（2019）提出的數(shù)值方法驗(yàn)證本文提出的橢圓形截面柱體動(dòng)水壓力的解析解，該方法實(shí)質(zhì)上是用垂向特征函數(shù)展開(kāi)，將三維輻射問(wèn)題簡(jiǎn)化為二維問(wèn)題；然后用外域特征函數(shù)展開(kāi)解與結(jié)構(gòu)截面附近內(nèi)域有限元聯(lián)合求解。圖4為本文橢圓柱體附加質(zhì)量系數(shù)的解與數(shù)值解的對(duì)比，橢圓柱的長(zhǎng)軸和短軸尺寸分別為a=20m、b=10m。由圖4可以看出，本文的解與橢圓柱數(shù)值解很好地吻合。

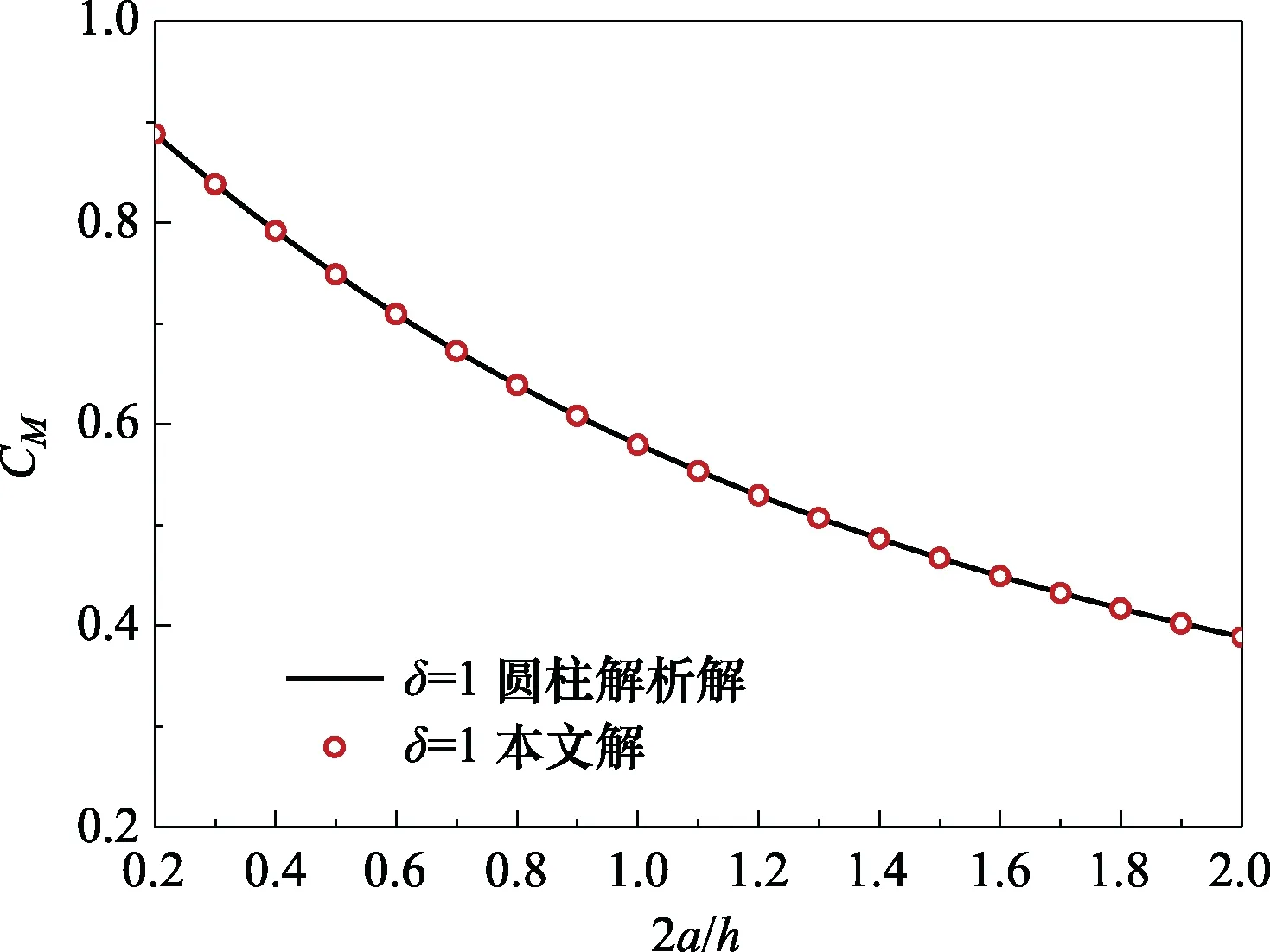
圖3 圓柱解析解與本文解的對(duì)比 Fig.3 The proposed solution compared with the analytical solution for circular cylinders and this paper

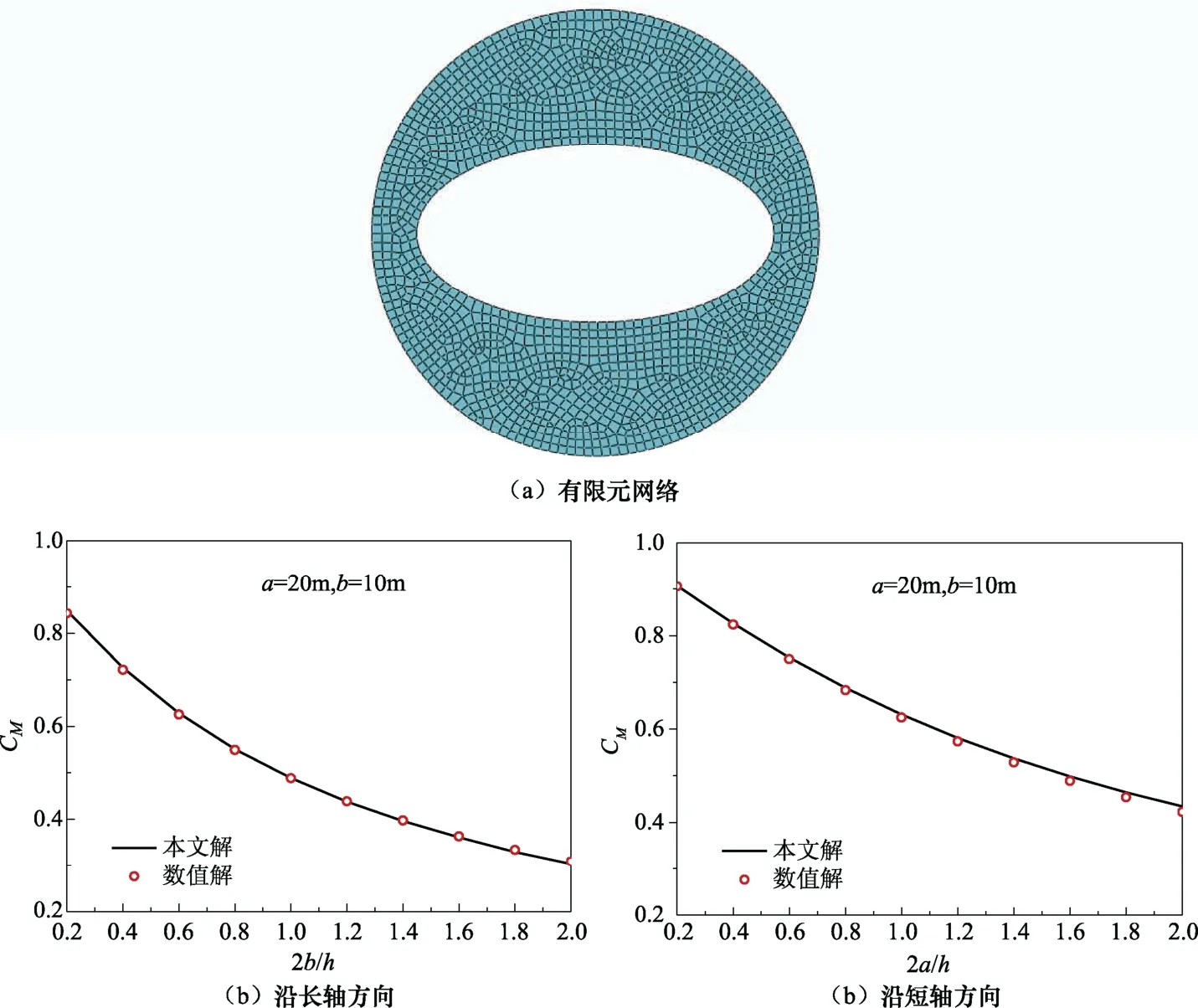
圖4 橢圓柱數(shù)值解與本文解的對(duì)比 Fig.4 The proposed solution compared with the numerical solution for elliptical cylinders and this paper

2 水中橢圓柱體結(jié)構(gòu)的地震反應(yīng)求解

采用有限元方法將柔性柱體結(jié)構(gòu)離散為梁?jiǎn)卧瑒t地震作用下水中橢圓柱體的動(dòng)力方程為（王勖成，2003）：

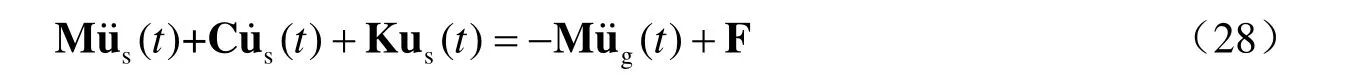
式中，M、C和K分別為結(jié)構(gòu)質(zhì)量、阻尼和剛度矩陣；us為結(jié)構(gòu)柔性位移列向量；F為地震 動(dòng)水力列向量。將地震動(dòng)水力式（24）或（26）進(jìn)行有限元離散，則F可以表示為

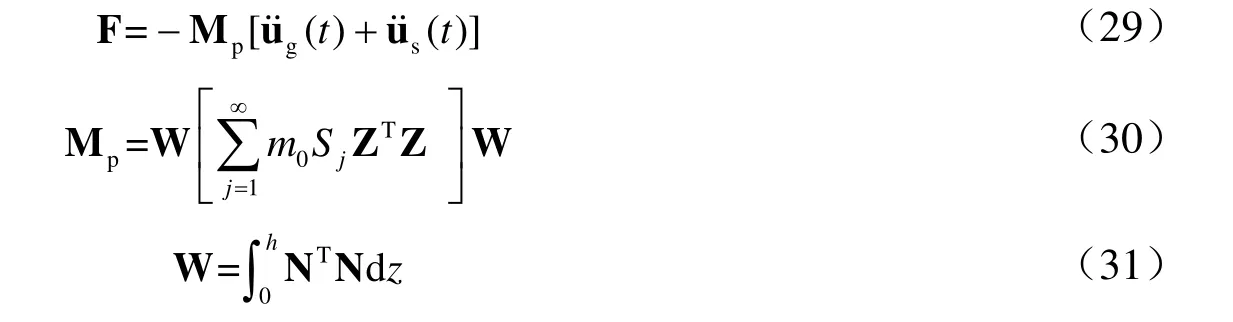
式中，Mp為附加質(zhì)量矩陣，N為形函數(shù)列向量；Sj如式（24b）或（26b）。

將式（29）代入式（28）整理得：

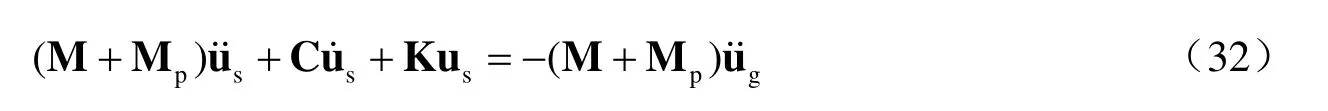
式（32）可通過(guò)數(shù)值積分方法Newmark-β方法求解（劉晶波等，2005）。需要指出的是，附加質(zhì)量矩陣Mp是滿陣的，難以在商業(yè)有限元中實(shí)現(xiàn)。本文將附加質(zhì)量矩陣Mp的每一行元素進(jìn)行集中化形成1個(gè)集中的附加質(zhì)量矩陣Mg，即：

式中，mi,j=mj,i，mi=mi,1+mi,2+ …… +mi,L-1+mi,L，L表示柱體結(jié)構(gòu)水下的節(jié)點(diǎn)數(shù)目。

通過(guò)柔性橢圓柱體驗(yàn)證提出的集中附加質(zhì)量矩陣的精度。圖5為地面運(yùn)動(dòng)位移，脈沖持時(shí)0.2s，頻譜覆蓋了地震作用頻段。橢圓柱體尺寸為H=80m、a=40m、b=20m、a1=30m、b1=15m；密度和彈性模量分別為2500kg/m3和30GPa；水深h=80m；梁?jiǎn)卧L(zhǎng)8m；不考慮阻尼作用。圖6為地面運(yùn)動(dòng)沿長(zhǎng)軸方向時(shí)，采用精確附加質(zhì)量模型和集中附加質(zhì)量模型計(jì)算得到的結(jié)構(gòu)頂部位移時(shí)程。由圖可見(jiàn)，采用集中附加質(zhì)量方法計(jì)算的位移反應(yīng)的周期偏大，即結(jié)構(gòu)柔性運(yùn)動(dòng)引起的水體附加質(zhì)量偏大。

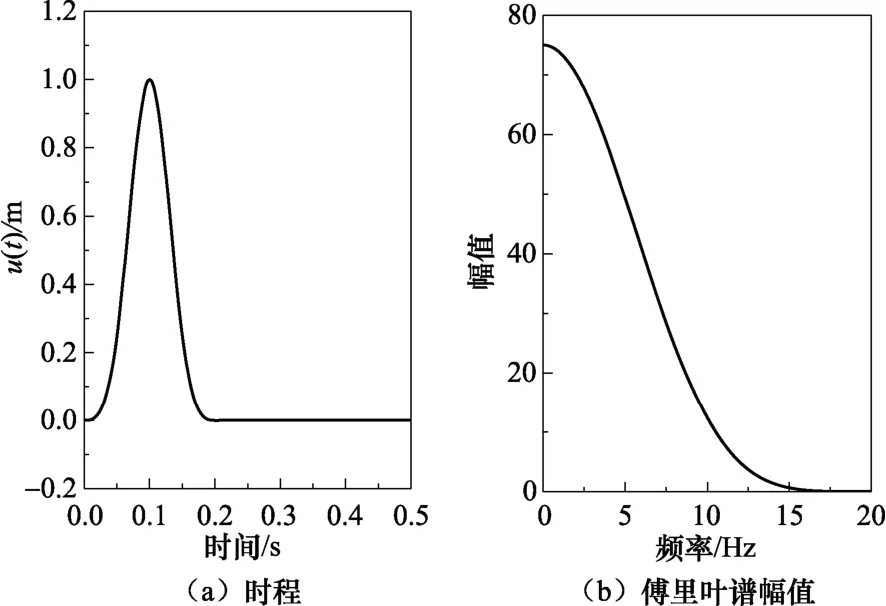
圖5 地面位移時(shí)程和傅里葉譜 Fig.5 The time history of displacement of the ground motion and its Fourier spectrum

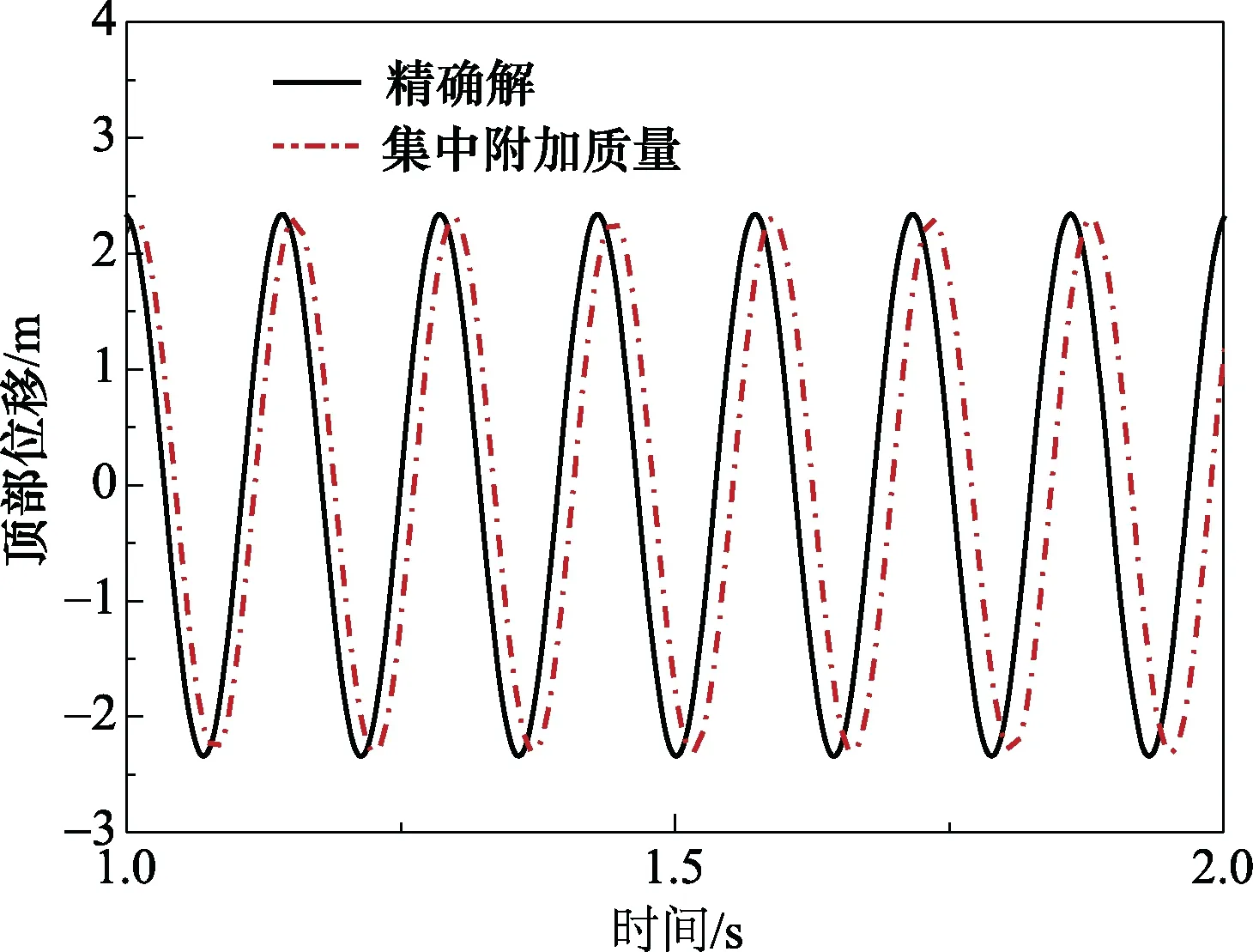
圖6 參考解和集中附加質(zhì)量模型位移時(shí)程的對(duì)比 Fig.6 The comparison of time history of displacement of the cylinder obtained by reference solution and lumped added mass method

因此，本文進(jìn)一步提出修正的集中附加質(zhì)量方法，即將式（32）修正為如下形式：

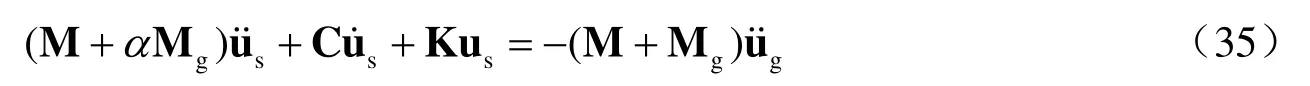
式中，α≤1為集中附加質(zhì)量矩陣修正系數(shù)。圖7為集中附加質(zhì)量矩陣修正系數(shù)隨無(wú)量綱參數(shù)寬深比（l）和長(zhǎng)短軸比（δ）的變化；無(wú)量綱參數(shù)寬深比（l）和長(zhǎng)短軸比（δ）的定義如公式（36）和（37）所示：

式中，地震方向沿x軸時(shí)D= 2a，地震方向沿y軸時(shí)D= 2b。

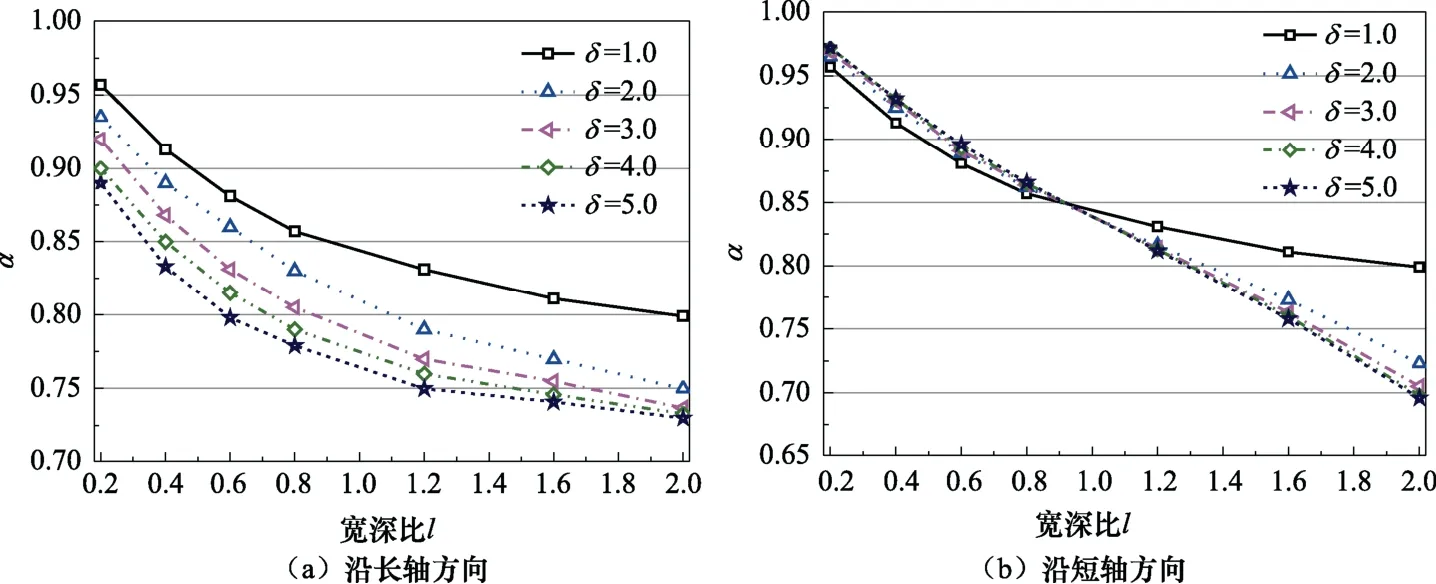
圖7 集中附加質(zhì)量修正系數(shù) Fig.7 Correction factors for the lumped added mass matrix

圖8為地面運(yùn)動(dòng)沿長(zhǎng)軸方向時(shí)，采用滿陣附加質(zhì)量模型和修正集中附加質(zhì)量模型計(jì)算得到的結(jié)構(gòu)頂部位移時(shí)程，滿陣附加質(zhì)量模型解為參考解。由圖可見(jiàn)，采用修正集中附加質(zhì)量方法計(jì)算的位移反應(yīng)與參考解很好地吻合。

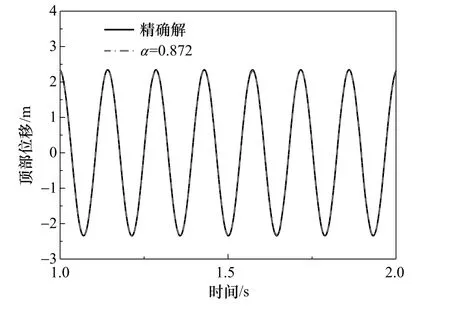
圖8 參考解和修正集中附加質(zhì)量模型的 位移時(shí)程比較 Fig.8 The comparison of time history of displacement of the cylinder obtained by reference solution and modified-lumped added mass method

3 橢圓形柱體均布附加質(zhì)量簡(jiǎn)化公式

式（34）所示的集中附加質(zhì)量矩陣與通過(guò)剛性結(jié)構(gòu)動(dòng)水力解析公式計(jì)算得到的附加質(zhì)量是一致的。需要指出的是，動(dòng)水力附加質(zhì)量解析公式的數(shù)學(xué)表達(dá)復(fù)雜，難以在工程中進(jìn)行應(yīng)用。因此，提出附加質(zhì)量的簡(jiǎn)化計(jì)算公式。假定附加質(zhì)量沿高度均勻分布，相應(yīng)的附加質(zhì)量系數(shù)定義如式（27）所示。將式（24a）或（26a）代入式（27）整理得：

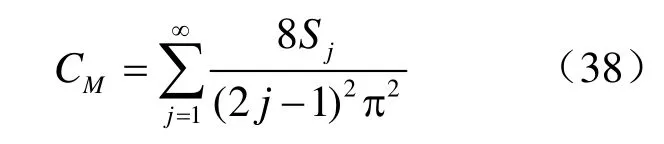
式中，Sj的定義見(jiàn)式（24b）或（26b）。需要指出的是，簡(jiǎn)化公式是在0.2 ≤l≤ 2和0.2 ≤δ≤5的范圍內(nèi)擬合得到的。

通過(guò)曲線擬合，圓形柱體均布附加質(zhì)量系數(shù)的簡(jiǎn)化公式為：

當(dāng)?shù)卣饎?dòng)沿長(zhǎng)軸方向時(shí)，通過(guò)曲線擬合得到橢圓形柱體沿長(zhǎng)軸方向的均布附加質(zhì)量系數(shù)的簡(jiǎn)化公式為：

當(dāng)?shù)卣饎?dòng)沿短軸方向時(shí)，通過(guò)曲線擬合，得到橢圓形柱體沿短軸方向的均布附加質(zhì)量系數(shù)的簡(jiǎn)化公式為：

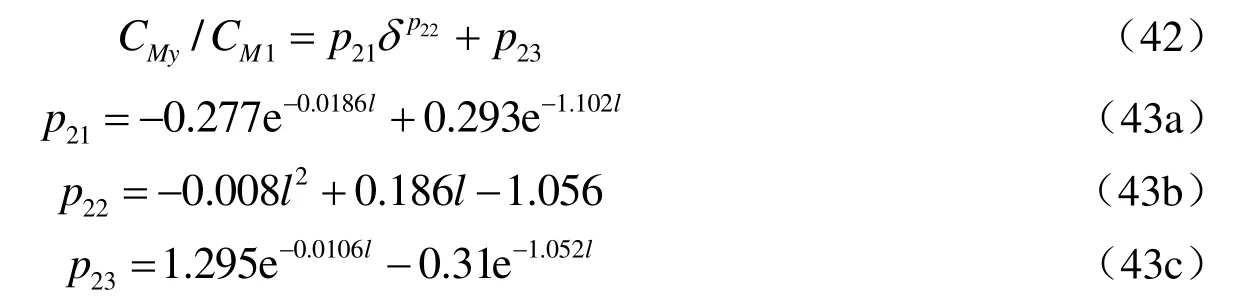
圖9為橢圓柱體附加質(zhì)量系數(shù)的解析解與簡(jiǎn)化公式的對(duì)比，圖10則為簡(jiǎn)化公式的誤差，可以看出簡(jiǎn)化公式與解析解吻合較好。

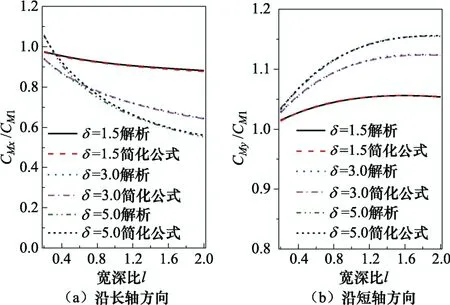
圖9 附加質(zhì)量系數(shù)解析解和簡(jiǎn)化公式的對(duì)比 Fig.9 The comparison of coefficient of the added mass obtained by analytical solution and simplified formula

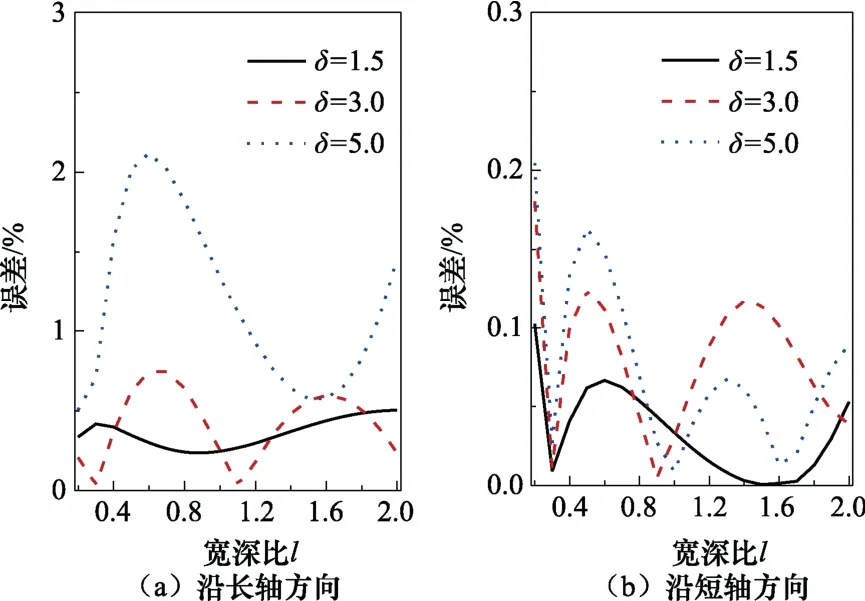
圖10 附加質(zhì)量系數(shù)簡(jiǎn)化公式的誤差 Fig.10 The error of the simplified formula for the added mass coefficient

4 結(jié)語(yǔ)

（1）基于橢圓坐標(biāo)系，采用分離變量法將拉普拉斯方程轉(zhuǎn)換為馬蒂厄方程。通過(guò)求解馬蒂厄方程，提出了橢圓柱體結(jié)構(gòu)地震動(dòng)水壓力的解析解。

（2）建立了地震作用下橢圓柱體結(jié)構(gòu)與水體相互作用的動(dòng)力有限元方程，結(jié)構(gòu)的動(dòng)水力通過(guò)附加質(zhì)量矩陣施加，該矩陣是滿陣的。

（3）為便于橢圓柱體結(jié)構(gòu)附加質(zhì)量矩陣在商業(yè)有限元中實(shí)現(xiàn)，提出了集中附加質(zhì)量矩陣的方法，該方法中柔性運(yùn)動(dòng)引起的附加質(zhì)量為集中附加質(zhì)量矩陣和修正系數(shù)的乘積。

（4）基于剛性柱體結(jié)構(gòu)動(dòng)水力的解析解，通過(guò)曲線擬合的方法建立了橢圓柱體結(jié)構(gòu)動(dòng)水力的均布附加質(zhì)量簡(jiǎn)化公式，公式中的系數(shù)僅與無(wú)量綱參數(shù)寬深比和長(zhǎng)短軸比相關(guān)。