巧用幾何直觀，化解思維難點

◆

(江蘇省常州市武進區(qū)實驗小學)

幾何直觀是小學數(shù)學教學中的熱點，也是難點。對幾何直觀的理解和應(yīng)用，仁者見仁，智者見智。新課標強調(diào)，要重視學生幾何直觀意識的培養(yǎng)，讓學生從幾何直觀學習實踐中，認識數(shù)學、理解數(shù)學。數(shù)學知識本身具有一定的抽象性，學生在認知時不能直觀認識。借助于幾何直觀，可以透過幾何直觀情境，以圖形、演示等直觀方式，來展現(xiàn)數(shù)學概念及方法，提高數(shù)學課堂教學成效。

一、挖掘數(shù)學與圖形的關(guān)系，品味“幾何直觀”內(nèi)涵

二、明確幾何直觀的價值，促進數(shù)學思維的形成

事實上，在幾何直觀教學應(yīng)用中，將幾何直觀作為圖形化教學的載體，來發(fā)展學生的空間觀念，提升學生的數(shù)學思維力。數(shù)學思維是解決數(shù)學問題的基礎(chǔ)，幾何直觀的應(yīng)用，豐富了學生頭腦中對數(shù)學問題的想象，也能夠從直觀地數(shù)學表征中，強化形象思維、創(chuàng)造性思維、邏輯性思維的培養(yǎng)。小學生正是形象思維向抽象思維過渡的關(guān)鍵期，對于形象化數(shù)學直觀的知識呈現(xiàn)，更能順應(yīng)學生形象思維發(fā)展需要。如在學習自然數(shù)時，我們引入數(shù)軸概念，讓學生從數(shù)軸上找出自然數(shù)的點，這些點，形成向往無限延伸的射線形狀。由此，從幾何直觀視角，認識到自然數(shù)與數(shù)軸圖形的對應(yīng)關(guān)系。在邏輯思維方面，借助于圖形直觀，來開發(fā)學生的想象力，增強對數(shù)學運算定律、數(shù)學公式的理解和應(yīng)用。如在學習“平行四邊形面積”時，如果我們直接給出面積計算公式，很多學生感到疑惑不解。我們可以先從長方形面積計算知識回顧教學中，讓學生復(fù)習長方形面積的計算方法。接著，提出平行四邊形的面積應(yīng)該如何計算？我們利用動手操作方式，用剪刀剪一個平行四邊形，然后，沿著中間任意一條高，剪開后，進行拼合成一個長方形。由此得到，平行四邊形的面積，與其等底等高長方形的面積相等，即平行四邊形面積等于底乘以高。同樣，在幾何直觀應(yīng)用中，還可以引領(lǐng)學生發(fā)現(xiàn)數(shù)學的奧妙，拓展解決數(shù)學問題的創(chuàng)新思維。讓學生能夠從數(shù)學思想與幾何直觀應(yīng)用中找到解決數(shù)學問題的思路，簡化解題難度。

三、探究幾何直觀，提供多元化解題路徑

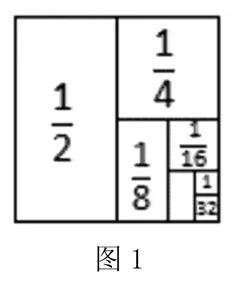
隨著學生知識結(jié)構(gòu)和年齡的增長，中高年級小學生的數(shù)學思維，處于具體運算向形式運算的過渡期。幾何直觀的運用，可以從圖形化解題分析中，將數(shù)學語言、數(shù)學符號轉(zhuǎn)換為直觀的圖形，幫助學生理解數(shù)學問題，感悟“數(shù)”與“形”的關(guān)系，也為提高解題能力創(chuàng)造條件。在學習“圖形與幾何”數(shù)學知識時，我們可以從幾何方法上，強調(diào)學生空間觀念的形成。如在學習“圖形的運動”時，對于“旋轉(zhuǎn)”的理解，很多學生感到難懂。我們可以將數(shù)學中的“旋轉(zhuǎn)”與生活中的“旋轉(zhuǎn)”進行對應(yīng)。通過實物旋轉(zhuǎn)方式，利用三角尺、直尺等旋轉(zhuǎn)，按照順時針、逆時針方向來觀察旋轉(zhuǎn)的角度，再將這些旋轉(zhuǎn)后的圖形畫在紙上。由此，從具體的實物“旋轉(zhuǎn)”來認識和理解“旋轉(zhuǎn)”概念，增強對數(shù)學方法的運用能力。還有，在運用幾何直觀教學時，可以化“看”為思，依托直觀的圖形來描述相應(yīng)的幾何問題，從而發(fā)現(xiàn)數(shù)學規(guī)律。在學習“長方體和正方體”時，對于長方體、正方體的特征分析，我們可以利用課件，讓學生觀察長方體的透視圖，然后利用擦除的方式，擦去一條棱，再擦去一條棱……從中觀察長方體的結(jié)構(gòu)變化。由此，從直觀的長方體圖形中，讓學生認識長、寬、高，以及頂點等概念，增強幾何直觀能力。在“數(shù)與代數(shù)”教學中，也可以利用幾何直觀，讓學生從表格、數(shù)軸、示意圖中挖掘數(shù)量關(guān)系。如在學習分數(shù)及其運算時，分數(shù)概念的理解，我們可以借助于“面積模型”，來將之直觀化呈現(xiàn)。某題中，有一杯水，第一次喝了半杯，第二次又喝了剩下的一半，如此每次都喝剩下的一半，喝了五次，共喝了多少水？如果我們直接將之轉(zhuǎn)換為“”顯然，很多學生感到疑惑不解。為此，我們通過對正方形面積的平分過程，如圖1所示。

總之，幾何直觀是小學數(shù)學教學中的重要思想，也是解決數(shù)學問題的有效方法。在數(shù)學領(lǐng)域，教師要注重幾何直觀的運用，通過形象化直觀圖形的呈現(xiàn)，讓學生能夠從中把握問題重點，化解難點。特別是對于中段學生，在形象思維向邏輯抽象思維過渡的關(guān)鍵期，借助于幾何直觀素養(yǎng)，來探究數(shù)學的本質(zhì)，發(fā)現(xiàn)數(shù)學的樂趣，提高學習數(shù)學的熱情，增強數(shù)學分析、解題能力。鼓勵學生從幾何直觀視角來審視數(shù)學問題，帶領(lǐng)學生從幾何直觀思維中辨析“數(shù)”與“形”的關(guān)系，提高數(shù)學創(chuàng)新思維力。