視覺導(dǎo)引受限下空間繩系機(jī)器人最優(yōu)逼近控制

胡永新，黃攀峰，孟中杰，劉正雄，張夷齋，董剛奇

(1. 西北工業(yè)大學(xué)航天學(xué)院智能機(jī)器人研究中心，西安 710072；2. 西北工業(yè)大學(xué)航天飛行動力學(xué)技術(shù)國家重點(diǎn)實(shí)驗(yàn)室，西安 710072)

0 引 言

空間繩系機(jī)器人由空間抓捕器，空間系繩，空間平臺三部分構(gòu)成，抓捕器通過系繩與平臺相連，如圖1所示，空間繩系機(jī)器人具有機(jī)動靈活，操作半徑大，安全性高等優(yōu)勢[1-2]。空間繩系機(jī)器人可用于太空垃圾移除[3-4]，目標(biāo)星輔助穩(wěn)定[5-6]等任務(wù)，是一種非常具有應(yīng)用前景的在軌操作工具，同時也是當(dāng)前在軌服務(wù)技術(shù)發(fā)展的熱點(diǎn)方向之一，國內(nèi)外學(xué)者對該空間繩系系統(tǒng)進(jìn)行了大量研究。

近年來有關(guān)空間繩系機(jī)器人的研究主要集中在動力學(xué)建模，逼近抓捕，抓捕后穩(wěn)定控制，拖曳移除，以及回收控制等。在動力學(xué)建模方面，文獻(xiàn)[7]介紹了基于無質(zhì)量輕質(zhì)桿模型，珠子模型，牛頓-歐拉方法，Ritz法，混合單元法，Galerkin法，Hamilton力學(xué)變分法等的空間系繩建模與求解方法。Yu等[8]針對空間柔性繩系衛(wèi)星系統(tǒng)釋放問題，采用簡化彈性桿模型分析了系繩長度釋放率，并在頻域分析了其穩(wěn)定性，得到了使繩系系統(tǒng)穩(wěn)定釋放的系繩伸長率的參數(shù)區(qū)域。Qi等[9]提出一種雙系繩空間繩系機(jī)器人概念，并對其動力學(xué)建模及控制問題進(jìn)行了研究。Zhang等[10]采用拉格朗日法對空間機(jī)器人、目標(biāo)組合體進(jìn)行建模，并對其動力學(xué)特性進(jìn)行了分析。

在抓捕后穩(wěn)定控制方面，William等[11]針對僅利用系繩的空間繩系機(jī)器人對目標(biāo)抓捕后復(fù)合體的消旋穩(wěn)定問題設(shè)計(jì)控制方法，該方法在系繩長度突然跳變情況下控制性能依然表現(xiàn)良好。文獻(xiàn)[12]研究了空間繩系機(jī)器人對目標(biāo)抓捕后復(fù)合體姿態(tài)接管控制問題，考慮了控制約束以及外部干擾，設(shè)計(jì)了有限時間終端滑模控制器，仿真結(jié)果校驗(yàn)了其控制器的良好性能。Zhai等[13]研究了空間繩系機(jī)器人系統(tǒng)中系繩對空間平臺干擾下空間平臺的姿態(tài)穩(wěn)定控制問題，考慮彈性系繩的擺動，建立了平臺姿態(tài)動力學(xué)方程，并設(shè)計(jì)了自適應(yīng)姿態(tài)控制器對平臺姿態(tài)進(jìn)行控制。

在對目標(biāo)拖曳移除方面，Chu等[14]針對空間繩系機(jī)器人大型空間垃圾移除問題，分析了系繩連接點(diǎn)偏置量的影響，并設(shè)計(jì)了安全準(zhǔn)則來對該空間系繩系統(tǒng)系繩纏繞風(fēng)險進(jìn)行分析。Wen等[15]針對空間繩系機(jī)器人對目標(biāo)離軌任務(wù)設(shè)計(jì)了僅有系繩長度反饋的系繩張力控制率，并實(shí)現(xiàn)了空間繩系機(jī)器人系統(tǒng)的穩(wěn)定控制。Wang等[16]研究了空間繩系機(jī)器人對目標(biāo)拖曳過程中的姿態(tài)穩(wěn)定控制問題，引入了系繩連接點(diǎn)的移動機(jī)構(gòu)，該機(jī)構(gòu)能夠?qū)崿F(xiàn)2自由度的旋轉(zhuǎn)和1自由度的伸縮，并設(shè)計(jì)了姿態(tài)前驅(qū)動抗飽和控制器，實(shí)現(xiàn)了抓捕復(fù)合體姿態(tài)的穩(wěn)定控制。

空間繩系機(jī)器人對目標(biāo)進(jìn)行逼近是其進(jìn)行其它任務(wù)的前提，在逼近抓捕任務(wù)方面，文獻(xiàn)[17]以空間繩系機(jī)器人對非合作目標(biāo)抓捕為背景，提出了一種新的目標(biāo)定位方法，所采用非合作目標(biāo)抓捕區(qū)域預(yù)測模型，大大減小了目標(biāo)搜索區(qū)域。文獻(xiàn)[18]針對空間繩系機(jī)器人近距離逼近問題設(shè)計(jì)了一種基于超扭滑膜觀測器的動態(tài)擬控制方法，實(shí)現(xiàn)了空間繩系機(jī)器人的近距離位姿跟蹤控制。孟中杰等[19]提出一種基于直線跟蹤的混合視覺伺服控制方法，該方法能夠保證在僅能獲得帆板支架邊緣線圖像信息的情況下，空間繩系機(jī)器人穩(wěn)定到達(dá)目標(biāo)衛(wèi)星的帆板支架處，并滿足捕獲條件。Botta等[20]對抓捕器與目標(biāo)的接觸碰撞過程進(jìn)行研究，建立了接觸碰撞動力學(xué)模型。黃攀峰等[21]針對空間繩系機(jī)器人目標(biāo)抓捕過程中的穩(wěn)定控制問題，設(shè)計(jì)了空間繩系機(jī)器人目標(biāo)抓捕魯棒自適應(yīng)穩(wěn)定控制器，該控制器能對模型中不確定性進(jìn)行補(bǔ)償，控制精度較高。Wang等[22]設(shè)計(jì)了一種協(xié)調(diào)控制機(jī)構(gòu)通過控制系繩連接點(diǎn)的移動充分利用系繩張力提供姿態(tài)控制力矩，其中在該機(jī)構(gòu)作用下，俯仰通道和偏航通道姿態(tài)控制均采用系繩張力力矩，滾轉(zhuǎn)通道采用推力器推力力矩，大大節(jié)省了燃料消耗。Zhang等[23]針對非合作目標(biāo)逼近問題提出了一種僅測角的逼近控制方案，該方案包括離線運(yùn)動規(guī)劃，模型預(yù)測控制和時延控制，仿真結(jié)果證明了該控制方案的有效性。

綜合以上已有研究可以發(fā)現(xiàn)，空間繩系機(jī)器人的最大特點(diǎn)是可以利用系繩提供軌道控制力以及姿態(tài)控制力矩對空間繩系機(jī)器人的位姿進(jìn)行控制，并且控制過程中系繩一般能夠提供遠(yuǎn)大于其推力器推力的張力，充分利用系繩張力作為控制量不僅能夠大大提高位置和姿態(tài)部分通道的控制的快速性，而且能夠節(jié)省燃料消耗。但采用系繩進(jìn)行控制時也會帶來明顯的問題，由于系繩張力矢量并不一直通過空間抓捕器的質(zhì)心，利用系繩張力進(jìn)行位置控制時，系繩張力會引入姿態(tài)干擾力矩，同時，運(yùn)用系繩張力力矩進(jìn)行姿態(tài)控制時，系繩張力會對抓捕器的軌道運(yùn)動產(chǎn)生影響。因而考慮這種操作耦合下姿軌一體化最優(yōu)控制很有必要。

在逼近任務(wù)過程中，抓捕器采用自身測量系統(tǒng)提供位姿信息進(jìn)行逼近，但限于空間繩系機(jī)器人的體積和重量，一般僅采用單/雙目相機(jī)來實(shí)現(xiàn)對目標(biāo)的測量[1]。一般情況下，遠(yuǎn)距離采用單目相機(jī)對目標(biāo)進(jìn)行測量，近距離采用雙目相機(jī)，但無論單目相機(jī)還是雙目相機(jī)，其相機(jī)視場角均有限。而任務(wù)一般要求在逼近過程中目標(biāo)一直處于空間抓捕器的相機(jī)視場范圍。但空間抓捕器的姿態(tài)運(yùn)動以及位置運(yùn)動均有可能使目標(biāo)脫離相機(jī)視場范圍。

另外需指出的是，當(dāng)逼近目標(biāo)為非合作目標(biāo)時，應(yīng)用單目相機(jī)進(jìn)行位置導(dǎo)航時，僅視線面內(nèi)面外角是單目相機(jī)可以直接測量的量，抓捕器相對目標(biāo)距離不可直接測量，因而這種相對導(dǎo)航信息不完全的逼近控制問題很有實(shí)際研究意義。

通過以上分析可知，空間繩系機(jī)器人對目標(biāo)最優(yōu)逼近的問題需同時兼顧軌道運(yùn)動和姿態(tài)運(yùn)動，并且在控制器設(shè)計(jì)中需考慮導(dǎo)航信息不全的影響。

本文結(jié)構(gòu)如下：第1節(jié)采用牛頓-歐拉法建立了空間繩系機(jī)器人動力學(xué)模型，以及逼近目標(biāo)相對軌道動力學(xué)模型。第2節(jié)采用高斯偽譜法進(jìn)行姿軌最優(yōu)軌跡一體化規(guī)劃，并設(shè)計(jì)了閉環(huán)控制率對最優(yōu)軌跡進(jìn)行跟蹤。第3節(jié)進(jìn)行了仿真校驗(yàn)。第4節(jié)對全文進(jìn)行了總結(jié)。

1 空間繩系機(jī)器人系統(tǒng)動力學(xué)模型

首先，在模型建立過程中采用以下假設(shè)：

1)平臺質(zhì)量遠(yuǎn)大于系繩和抓捕器的質(zhì)量，且推力器以及系繩張力對平臺的影響可以忽略不計(jì)。

2)平臺在任務(wù)期間保持姿態(tài)穩(wěn)定，將平臺視為質(zhì)點(diǎn)忽略其姿態(tài)對系繩及抓捕器的影響。

3)逼近過程中，系繩連接點(diǎn)在抓捕器本體系下不移動。

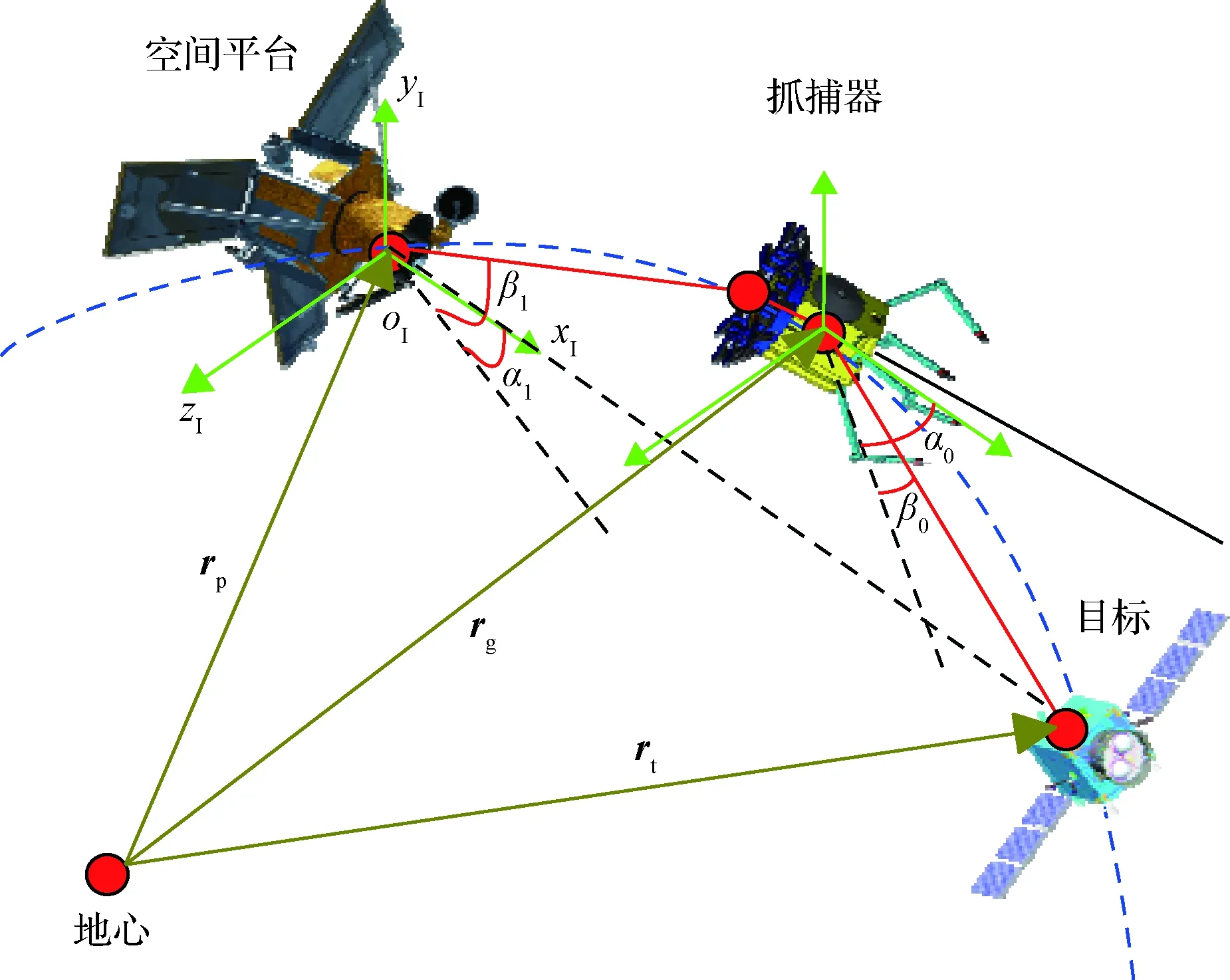
圖2 空間繩系機(jī)器人對目標(biāo)逼近Fig.2 The gripper approaching the target

1.1 逼近目標(biāo)相對軌道動力學(xué)模型

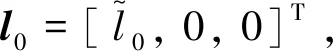
(1)

式中:ωvI為抓捕器視線坐標(biāo)系相對慣性坐標(biāo)系的旋轉(zhuǎn)角速度。

fg為作用在抓捕器上的空間干擾力矢量，ft為作用在目標(biāo)上的空間干擾力矢量，Tg為作用在抓捕器上空間系繩張力矢量，F(xiàn)g為作用在抓捕器上推力器推力矢量，F(xiàn)t為作用在目標(biāo)上推力器推力矢量，mt為目標(biāo)質(zhì)量，mg為抓捕器質(zhì)量，μ為地球引力常數(shù)，則目標(biāo)及抓捕器的相對軌道動力學(xué)方程為：

(2)

其中，Δggt為抓捕器和目標(biāo)的引力加速度差。將Δggt投影到抓捕器視線坐標(biāo)系可得：

(3)

式中:Δgvgt,rvg和rvt分別為Δggt,rg和rt在抓捕器視線坐標(biāo)系下的投影，且rvg=rvt-l0。

將式(3)在l0=0處展開，并忽略高階項(xiàng)可得：

(4)

式中：a,n,e及θ分別為目標(biāo)軌道的長半軸、角速度、偏心率、真近點(diǎn)角。

結(jié)合式(1)和式(4)，式(2)在抓捕器視線系下描述為：

(5)

式中:vft，vFt，vfg，vTg，vFg分別為ft,Ft,fg,Tg,Fg在抓捕器視線坐標(biāo)系下的投影。

1.2 空間系繩無質(zhì)量彈性桿模型

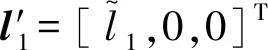
平臺受到系繩張力矢量為-Tg，根據(jù)假設(shè)可以忽略。抓捕器質(zhì)心受到系繩張力矢量為Tg，受到自身執(zhí)行器控制力矢量為Fg。則該部分動力學(xué)方程為：

(6)

(7)

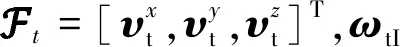
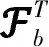
(8)

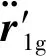
(9)

其中，Δgpgt為Δgpg在系繩坐標(biāo)系下的投影。

則式(6)在系繩坐標(biāo)系下的投影為：

(10)

式中：tFg，tfeg，tTg=[-Tl,0,0]T分別為系繩坐標(biāo)系下抓捕器控制力、環(huán)境干擾力、系繩控制力。

由于系繩僅有張緊力沒有壓緊力，因而：

(11)

式中:E為空間系繩拉伸彈性模量，A為空間系繩橫截面積，σ=(l1-ls)/ls,ls為已釋放系繩的自然長度，c為空間系繩等效黏性阻尼系數(shù)。

1.3 抓捕器姿態(tài)動力學(xué)模型

任務(wù)過程中，抓捕器受到的力矩主要有：抓捕器控制力矩、系繩張力力矩以及環(huán)境干擾力矩，有：

(12)

式中：Ib為抓捕器在其本體系下的慣性張量；bτc，bτe分別為抓捕器本體系下抓捕器控制力矩，系繩張力力矩以及環(huán)境干擾力矩。Cbt為抓捕器本體系到系繩坐標(biāo)系的旋轉(zhuǎn)矩陣。

2 逼近目標(biāo)最優(yōu)控制

2.1 最優(yōu)軌跡規(guī)劃問題描述

空間平臺距目標(biāo)100 m停靠并調(diào)整位姿，確保目標(biāo)在抓捕器相機(jī)視場中心時釋放抓捕器，抓捕器以一定初速向目標(biāo)逼近，逼近至距目標(biāo)一定距離。假設(shè)目標(biāo)不進(jìn)行自主機(jī)動，且其軌道偏心率e=0，忽略環(huán)境干擾等影響，研究空間繩系機(jī)器人抓捕器從逼近到距目標(biāo)20 m的逼近最優(yōu)軌道設(shè)計(jì)。

1)指標(biāo)函數(shù)

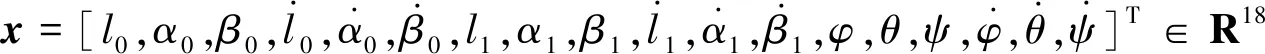
(13)

其中，up=[mgQl2,mgQα,mgQβ]T為軌道控制輸入推力器部分，ua=[Qφ,Qθ,Qψ]T為姿態(tài)控制力矩，κ1,κ2∈R3×3為系數(shù)矩陣，且需根據(jù)實(shí)際的推力及推力力矩關(guān)系進(jìn)行選擇。

2)約束函數(shù)

優(yōu)化問題中約束主要有動力學(xué)方程約束，邊界條件約束，控制約束以及狀態(tài)約束。

式(5)、式(10)和式(12)為該問題的動力學(xué)方程約束。

令x0為空間繩系機(jī)器人系統(tǒng)的初始狀態(tài)，則：

x(t0)=x0

(14)

(15)

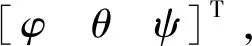
(16)

當(dāng)γ≤ζ時，目標(biāo)一直處于抓捕器相機(jī)視場范圍。顯然任務(wù)中α0,β0,θ,ψ的幅值均小于0.25ζ時，可以保證γ≤ζ一直成立。因而建立下列狀態(tài)約束：

(17)

同時需要考慮控制約束

uL≤u≤uR

(18)

其中，u∈R7為控制變量，uL與uR分別為控制變量的下限與上限。

2.2 高斯偽譜法規(guī)劃模型建立

對于最優(yōu)軌跡規(guī)劃問題，求解方法分為間接法和直接法[26]。間接法精度高但對初值估計(jì)困難。直接法收斂域?qū)挘瑢Τ踔倒烙?jì)要求不高。高斯偽譜法作為一種求解最優(yōu)化問題的直接法，具有較高求解精度，在一系列最優(yōu)控制問題中得到采用。文獻(xiàn)[27]采用高斯偽譜法對失效航天器超近距逼近問題規(guī)劃最優(yōu)避免碰撞逼近軌跡。文獻(xiàn)[28]將高斯偽譜法應(yīng)用于液體運(yùn)載火箭拋罩結(jié)束到入軌飛行段的制導(dǎo)方法中得到了滿意的結(jié)果。文獻(xiàn)[29]將高斯偽譜法應(yīng)用于多UAV協(xié)同航跡規(guī)劃，獲得了滿足任務(wù)要求的可行飛行軌跡。本文采用高斯偽譜法對空間繩系機(jī)器人最優(yōu)逼近問題進(jìn)行求解。利用高斯偽譜法將最優(yōu)軌跡規(guī)劃問題離散化并轉(zhuǎn)化為NLP問題。

Gauss偽譜法通過時域變換、Lagrange多項(xiàng)式差值將時間t∈[t0,tf]上的最優(yōu)控制問題轉(zhuǎn)化為τ∈[-1,1]上的非線性規(guī)劃問題。

(19)

其中，τ1～τK為Legendre-Gauss多項(xiàng)式的K個零點(diǎn)，X為離散狀態(tài)變量，U為離散輸入變量，Dki為微分矩陣，且滿足如下關(guān)系：

(20)

末端狀態(tài)約束可以轉(zhuǎn)化為：

(21)

式中:ωk為第k處的高斯積分系數(shù)。

目標(biāo)函數(shù)可以轉(zhuǎn)化為：

(22)

狀態(tài)變量和控制變量在各離散點(diǎn)處的約束為：

(23)

2.3 閉環(huán)控制器設(shè)計(jì)

在空間繩系機(jī)器人系統(tǒng)抓捕機(jī)構(gòu)在遠(yuǎn)距離逼近時僅采用單目相機(jī)作為相對位置測量裝備，但單目相機(jī)僅能夠直接測量目標(biāo)方位角信息。因而本文所設(shè)計(jì)控制器利用目標(biāo)方位角，系繩長度以及絕對姿態(tài)角的測量信息實(shí)現(xiàn)空間繩系機(jī)器人的位姿跟蹤控制。所設(shè)計(jì)控制器結(jié)構(gòu)如圖3所示。

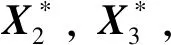
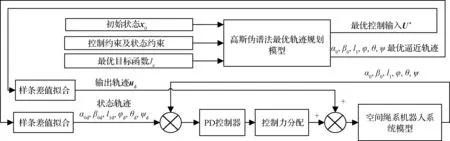
圖3 閉環(huán)最優(yōu)控制系統(tǒng)框架Fig.3 The closed-loop optimal control system

3 仿真校驗(yàn)

3.1 仿真條件

空間繩系機(jī)器人的基本參數(shù)如下：空間繩系機(jī)器人質(zhì)量36 kg，慣量：Ix=0.6 kg·m2,Iy=2.1 kg·m2,Iz=2.2 kg·m2；連接點(diǎn)在抓捕器本體系下位置為[-0.25 m，0，0]T；軌控推力器推力幅值2 N，姿控推力器推力力矩為0.1 Nm，抓捕器控制力矩幅值為0.1 Nm；抓捕器單目相機(jī)視場角為0.4 rad；系繩楊氏模量130 Gpa，系繩直徑1 mm，等效黏性阻尼系數(shù)為0.1，系繩張力范圍為0.02 N～10 N；為保證系繩一直處于張緊狀態(tài)，令系繩一直有張力且張力最小為0.02 N。抓捕器脫離平臺后，向目標(biāo)進(jìn)行逼近，實(shí)現(xiàn)對目標(biāo)從100 m到20 m的逼近。

表1 仿真關(guān)鍵參數(shù)列表Table 1 Key simulation parameters

3.2 仿真算例一

在MATLAB環(huán)境下對高斯偽譜法規(guī)劃模型進(jìn)行求解得到理想控制輸入和理想狀態(tài)軌跡，將理想控制輸入進(jìn)行樣條差值，并將差值得到的結(jié)果作為實(shí)際控制量，得到仿真結(jié)果如圖4～圖10所示。其中圖4～圖6為控制輸入曲線，可以看出所規(guī)劃控制輸入均滿足控制變量上下限約束。在軌道控制方面，x軸方向上的減速主要由系繩張力實(shí)現(xiàn)，節(jié)省了推力器燃料消耗。u2～u7均得到的很好的擬合，但u1擬合效果并不理想，在13 s～18 s以及95 s～100 s期間實(shí)際輸入與期望之間存在有較大的偏差。

圖7為慣性系下抓捕器相對目標(biāo)運(yùn)動軌跡，可以看出實(shí)際軌跡逐漸偏離期望軌跡。圖8為抓捕器絕對姿態(tài)變化曲線，可以看出絕對姿態(tài)在三個通道跟蹤效果均不理想，特別是姿態(tài)角θ在任務(wù)期間最大值為0.2322 rad，大于規(guī)劃中設(shè)置上限0.1 rad。從圖9可以看出，系繩張力力矩存在較大偏差，該偏差直接導(dǎo)致姿態(tài)跟蹤偏差。可見系繩控制輸入的擬合偏差對逼近過程具有較大影響，特別是系繩控制輸入擬合偏差不僅對軌道跟蹤產(chǎn)生影響，其產(chǎn)生的系繩力矩偏差會對姿態(tài)軌跡跟蹤產(chǎn)生較大影響。

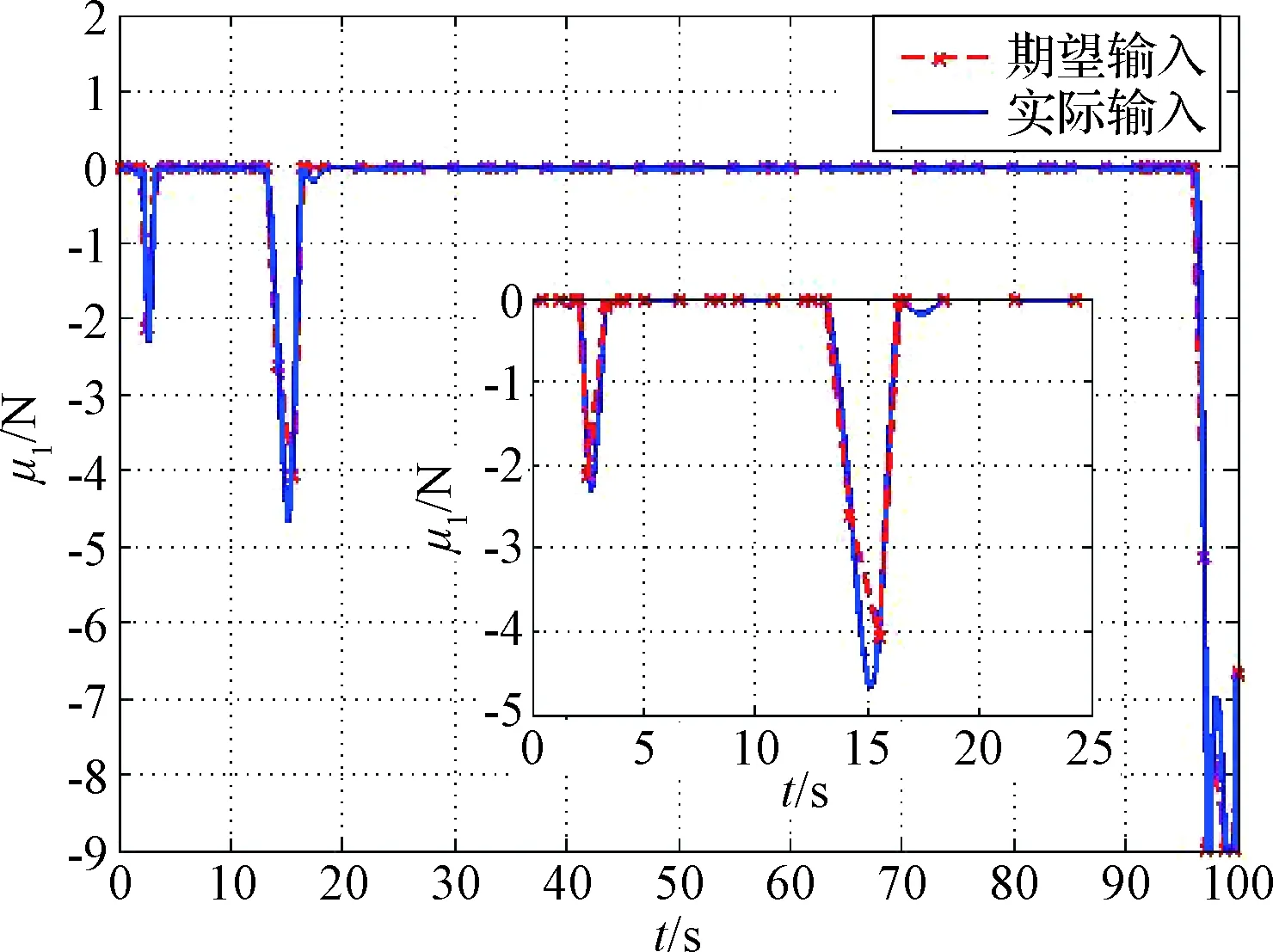
圖4 系繩控制力Fig.4 The control force of tether

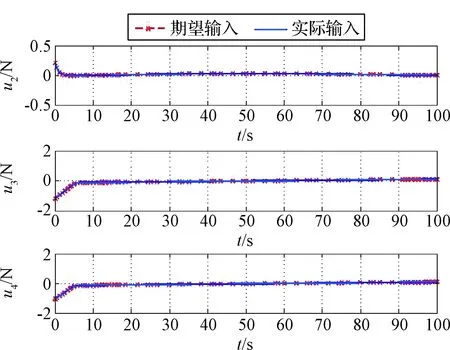
圖5 軌道控制中推力器控制力部分Fig.5 The control force of thrusters

圖6 姿態(tài)控制力矩Fig.6 The control torques

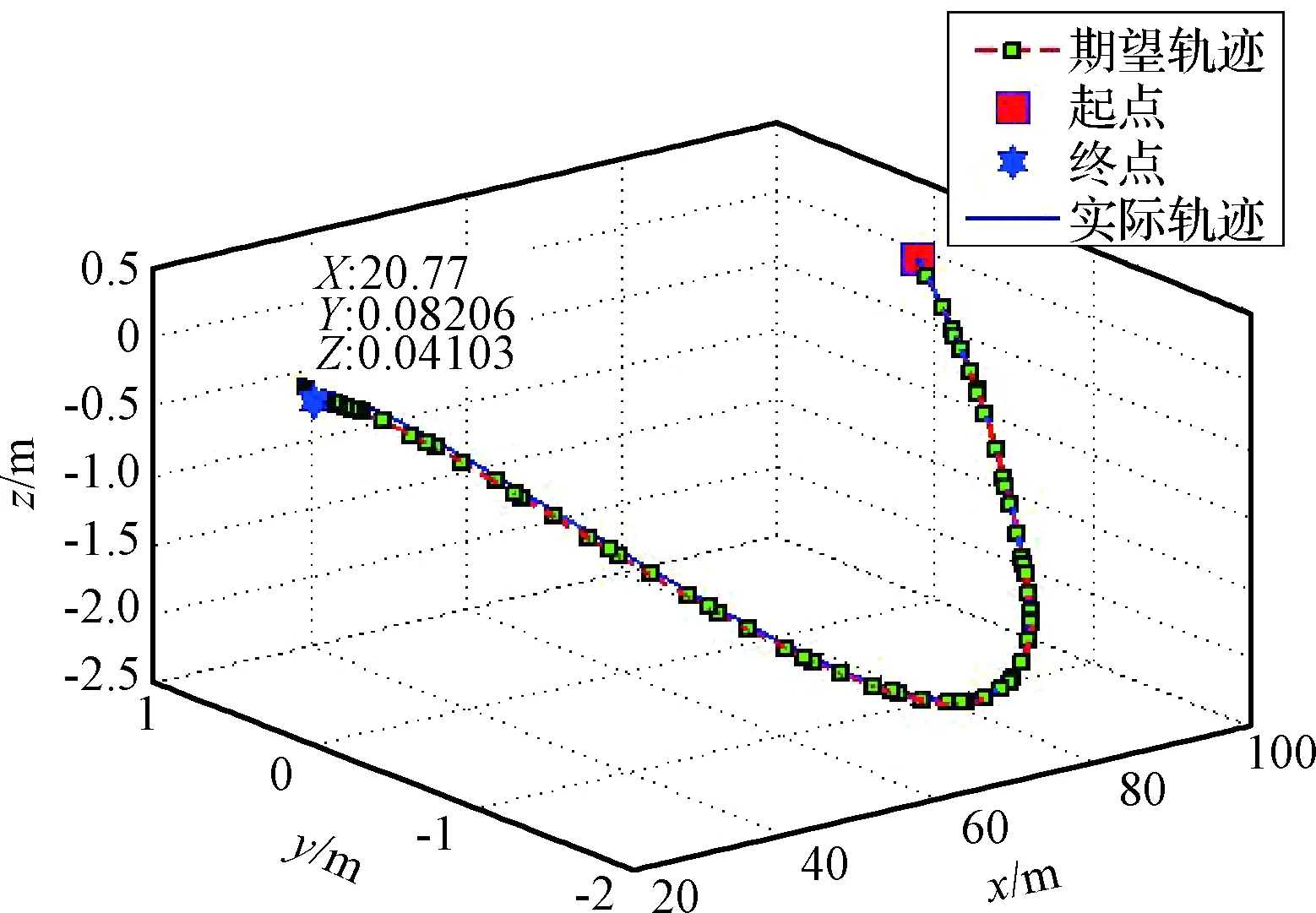
圖7 慣性坐標(biāo)系下抓捕器與目標(biāo)之間相對運(yùn)動軌跡Fig.7 The trajectory of the gripper relative to target with respect to oIxIyIzI

任務(wù)期間抓捕器視線角如圖10所示，可以看出在整個任務(wù)過程中視線角均小于0.22 rad，目標(biāo)全程均在抓捕器相機(jī)的視場范圍內(nèi)，滿足任務(wù)要求，但可以看出視線角在52 s左右達(dá)到峰值，這是由姿態(tài)角θ和ψ在52 s左右達(dá)到極值導(dǎo)致。最終抓捕器與目標(biāo)的相對位置為[20.77 m,0.08 m,0.04 m]，與所規(guī)劃的期望最終位置之間的偏差為[0.77 m, 0.08 m,0.04 m]，最終姿態(tài)角與期望姿態(tài)角的偏差為[0.024 rad,0.2 rad,-0.04 rad],可見采用該開環(huán)控制方案，軌跡跟蹤存在較大末端控制偏差。

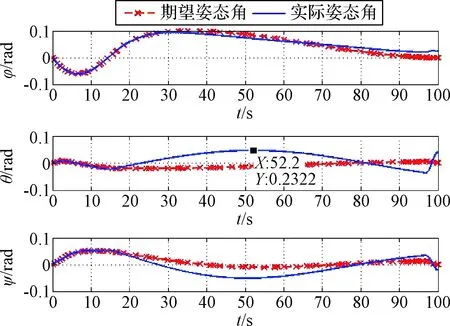
圖8 抓捕器絕對姿態(tài)變化曲線Fig.8 The attitude angle of the gripper

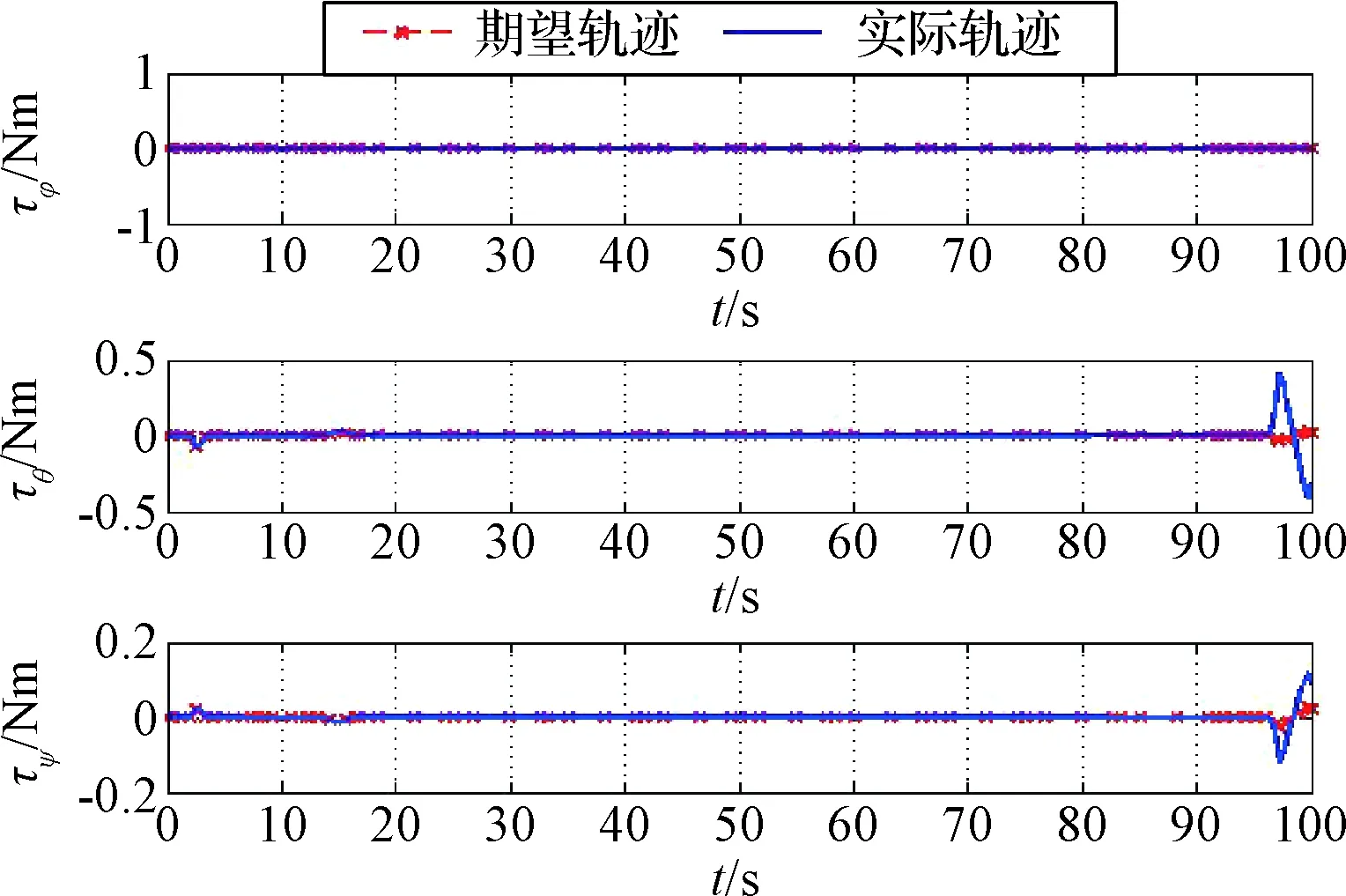
圖9 系繩張力力矩Fig.9 Torques produced by the tether

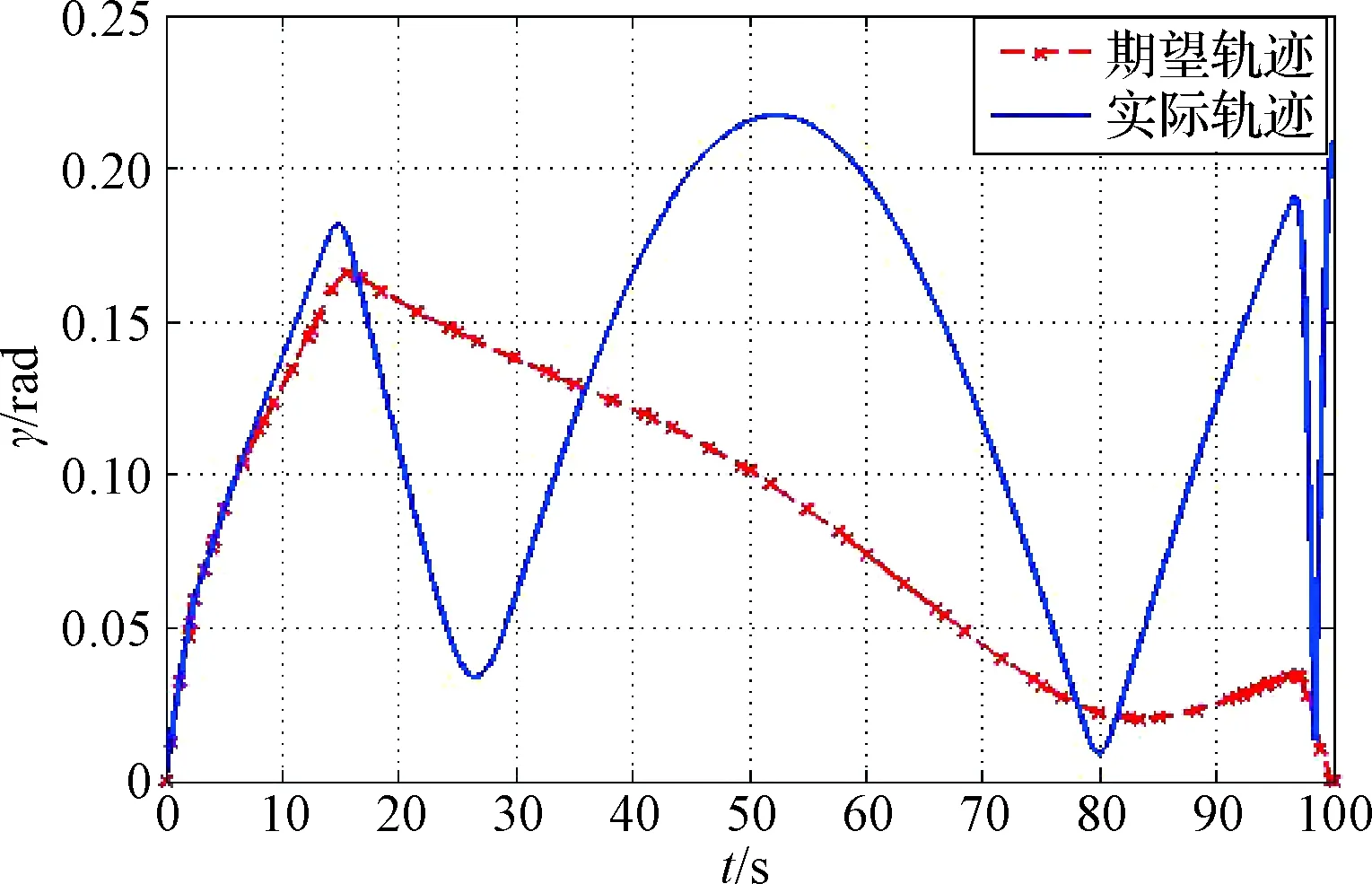
圖10 抓捕器視線角變化曲線Fig.10 The sight-line angle of the gripper

3.3 仿真算例二

對第2.3節(jié)所設(shè)計(jì)的閉環(huán)控制框架進(jìn)行了仿真校驗(yàn)，仿真結(jié)果如圖11～圖16所示。其中圖11～圖13為控制輸入曲線，可以看出控制輸入均滿足幅值約束條件，控制輸入u1,u2,u6的軌跡與期望軌跡存在較大偏差，其中u1的偏差和仿真算例一中相同，主要為擬合偏差。u2和u6的偏差為PD控制器產(chǎn)生的控制量對狀態(tài)偏差進(jìn)行補(bǔ)償控制。

圖14為慣性坐標(biāo)系下抓捕器與目標(biāo)之間相對運(yùn)動的軌跡。圖15為抓捕器絕對姿態(tài)角變化曲線，可以看出實(shí)際軌跡與期望軌跡重合度較高。最終抓捕器與目標(biāo)的相對位置為：[19.99 m, 3.8×10-4m, -1.4×10-3m]，與所規(guī)劃的期望最終位置之間的偏差為[-0.01 m, 3.8×10-4m, -1.4×10-3m]，最終姿態(tài)角與期望姿態(tài)角的偏差為[-1×10-6rad, 2×10-3rad, 5×10-4rad]。從圖16可以看出，在整個任務(wù)中抓捕器視線角變化軌跡與期望軌跡基本一致且均小于0.18 rad，滿足相機(jī)視場角約束。

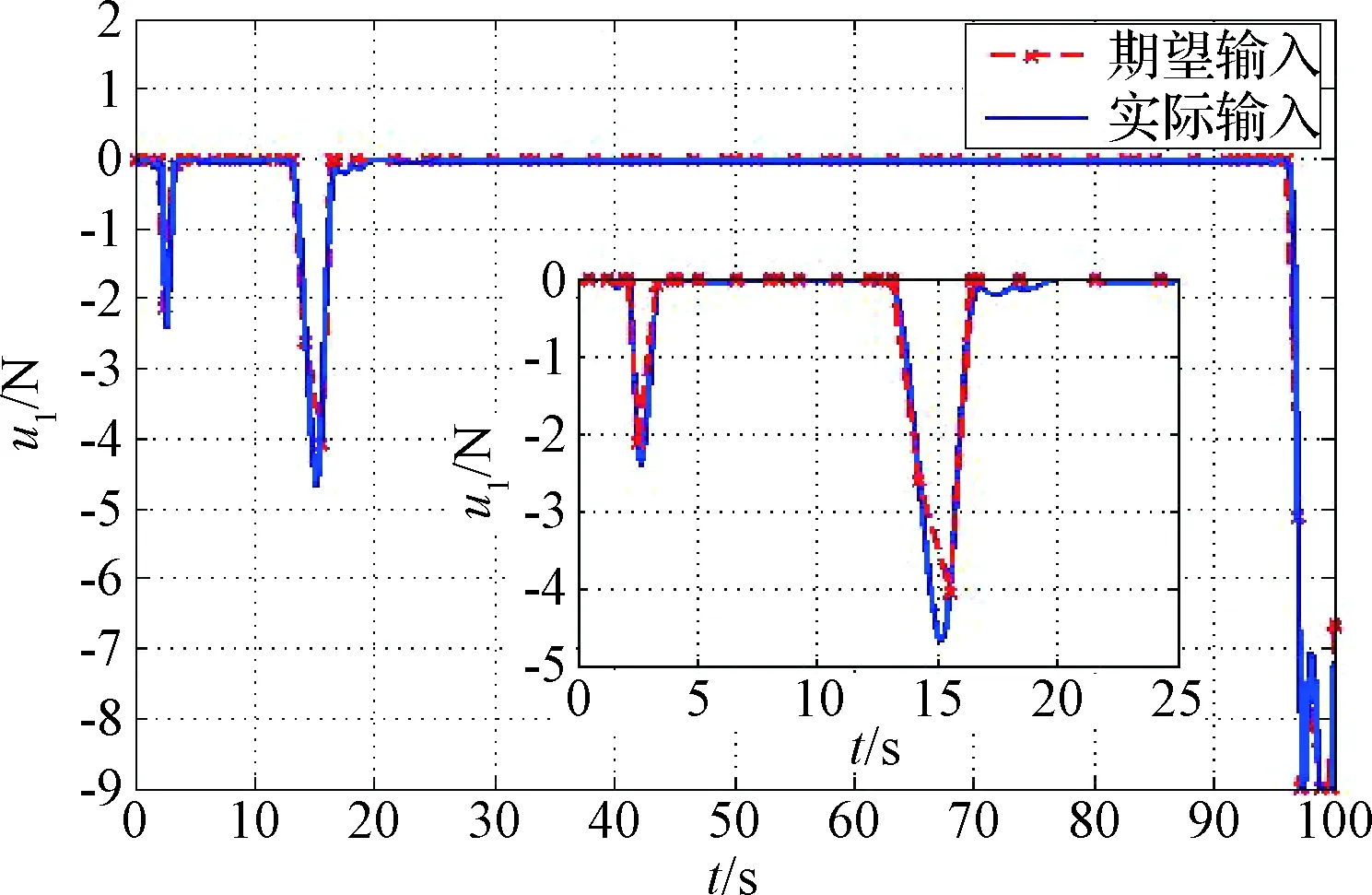
圖11 系繩控制力Fig.11 The control force of the tether

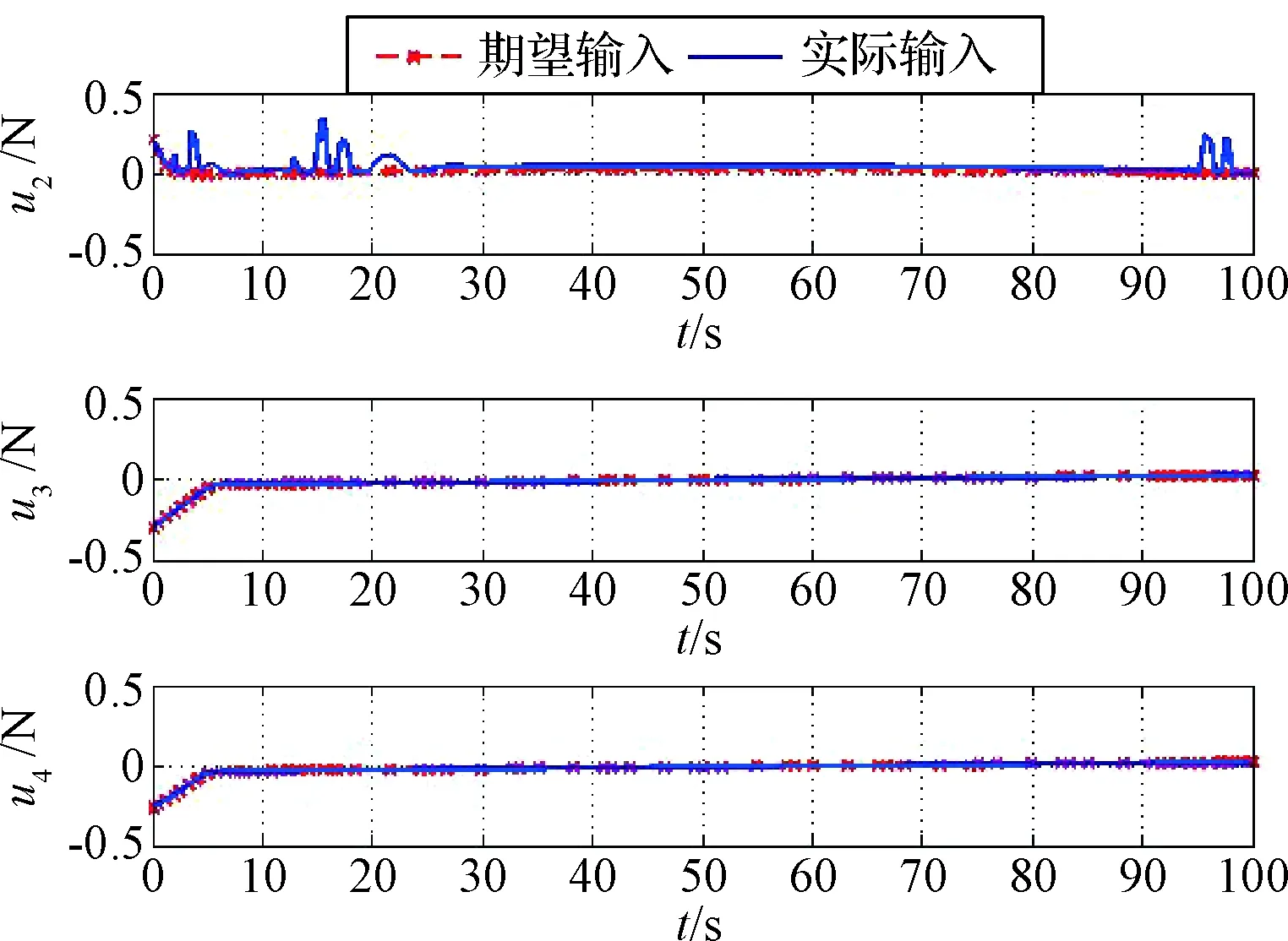
圖12 軌道控制中推力器控制力部分Fig.12 The control force of thrusters

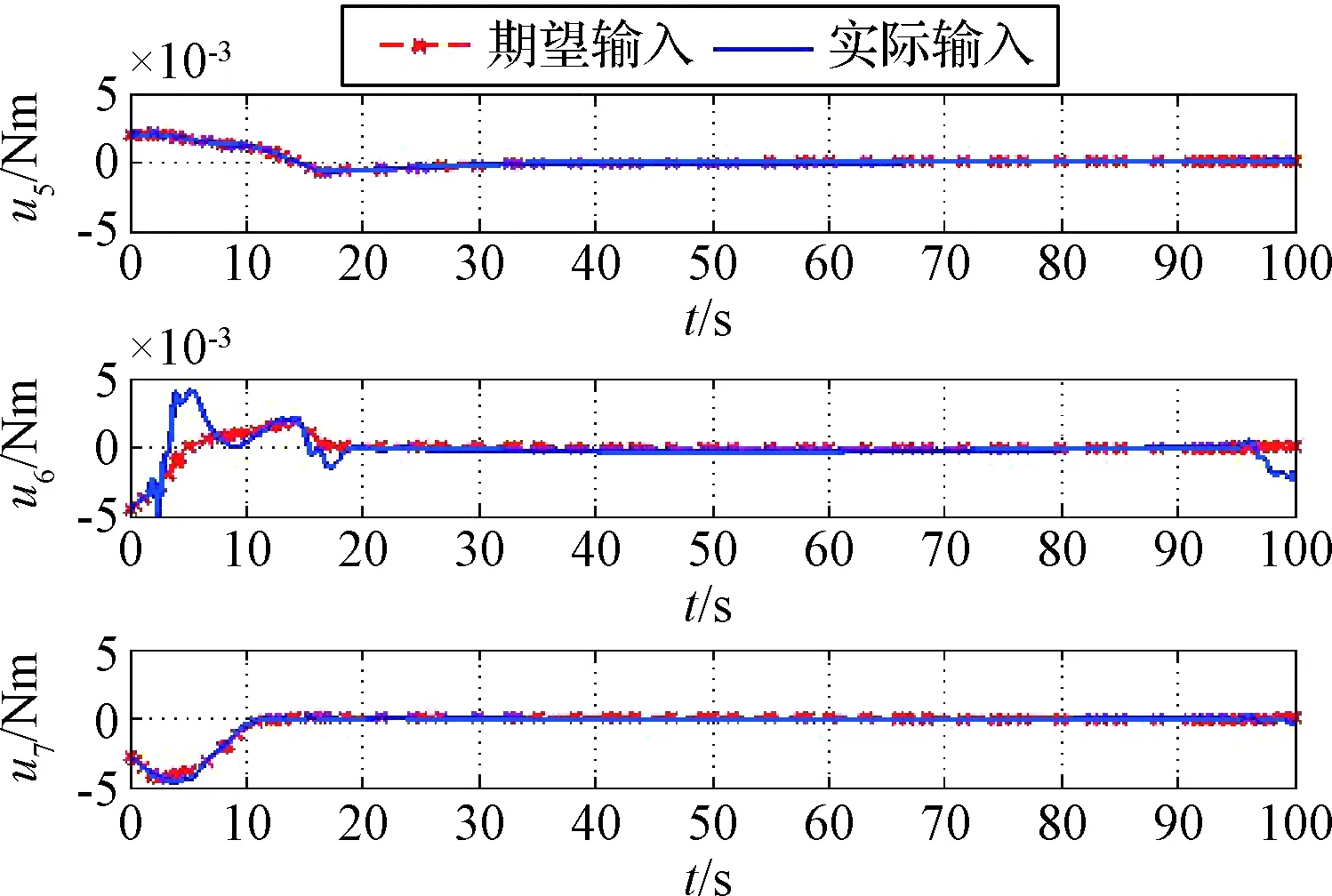
圖13 姿態(tài)控制力矩Fig.13 The control torques

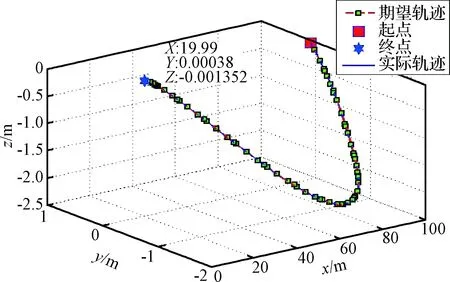
圖14 慣性坐標(biāo)系下抓捕器與目標(biāo)之間相對運(yùn)動軌跡Fig.14 The trajectory of the gripper relative to target with respect to oIxIyIzI

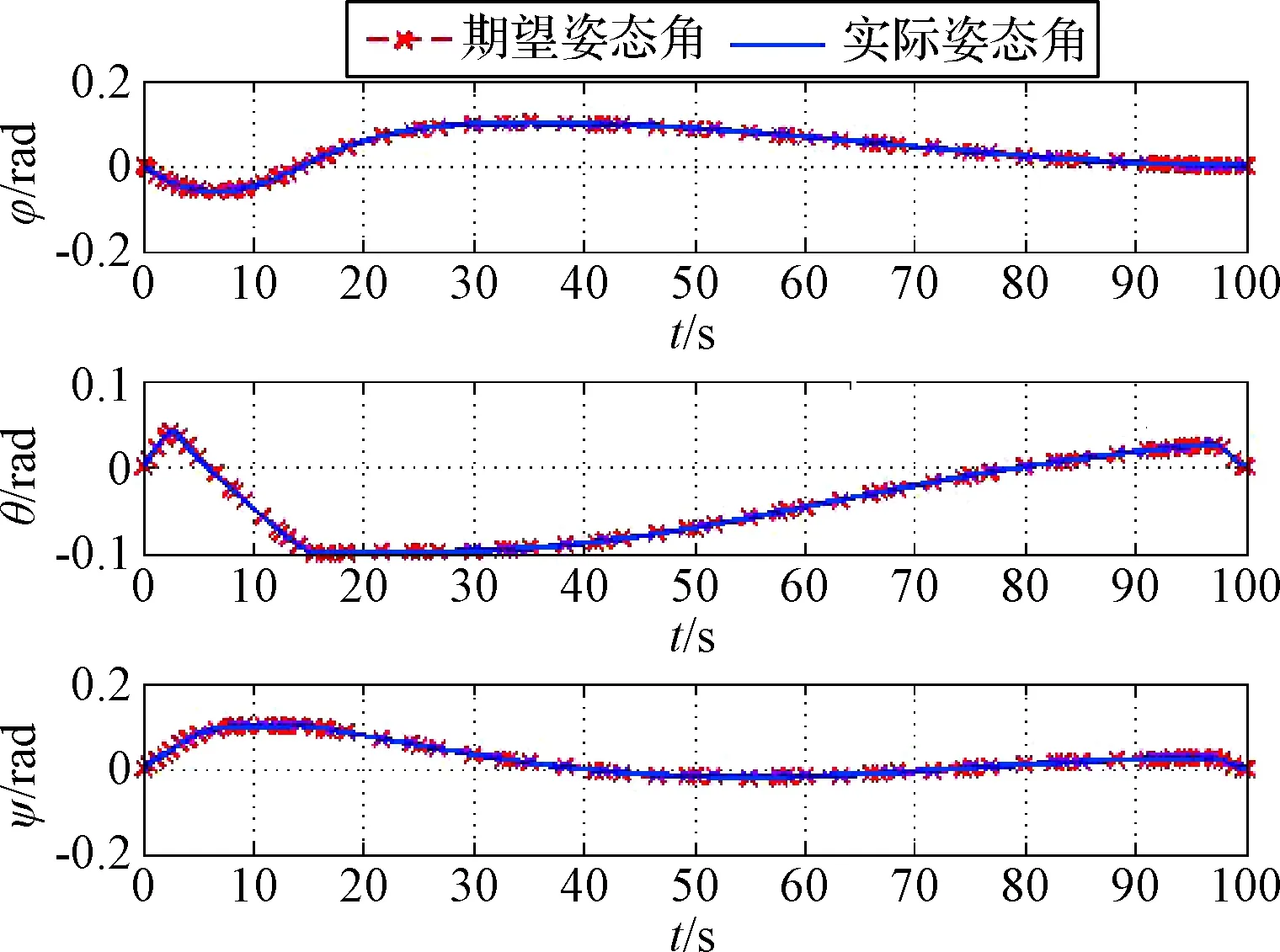
圖15 抓捕器絕對姿態(tài)變化曲線Fig.15 The attitude angle of the gripper

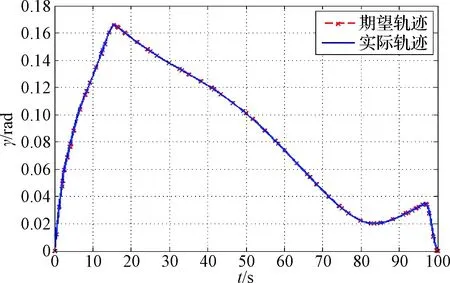
圖16 抓捕器視線角變化曲線Fig.16 The sight-line angle of the gripper

4 結(jié) 論

本文針對空間繩系機(jī)器人對非合作目標(biāo)最優(yōu)逼近問題進(jìn)行研究。考慮抓捕器視線角約束，對空間繩系機(jī)器人姿軌最優(yōu)軌跡一體規(guī)劃，并設(shè)計(jì)了閉環(huán)最優(yōu)控制系統(tǒng)對規(guī)劃軌跡進(jìn)行跟蹤控制，該方案中位置跟蹤僅需目標(biāo)方位角信息和系繩長度信息，克服了單目相機(jī)距離信息測量不足的缺點(diǎn)，實(shí)現(xiàn)了無需測量抓捕器與目標(biāo)相對距離的相對位置逼近。仿真結(jié)果表明,該閉環(huán)控制系統(tǒng)能夠保證目標(biāo)在整個任務(wù)期間一直處于抓捕器相機(jī)視場范圍內(nèi)，且具有較高的末端控制精度。需要指出的是：在本文的研究中，系繩彈性桿模型較為簡化，忽略了系繩質(zhì)量的影響以及空間平臺位姿機(jī)動控制的影響，下一步研究工作將把系繩珠點(diǎn)模型以及平臺位姿機(jī)動控制考慮進(jìn)繩系機(jī)器人系統(tǒng)模型中，分析其對繩系機(jī)器人逼近任務(wù)的影響。