一種應用于空間碎片演化模型的碰撞概率算法
王曉偉,劉 靜,崔雙星
(1. 中國科學院國家天文臺,北京 100101;2. 國家航天局空間碎片監測與應用中心,北京 100101; 3. 中國科學院大學,北京 100049)
0 引 言
近年來,空間碎片數量激增使得在軌航天器的運行安全受到極大威脅,Kessler雪崩效應再次被提及[1]。空間碎片數量不斷增長引發了國際上關于空間碎片環境長期穩定性的研究,空間碎片環境長期演化模型成為該領域的國際研究熱點之一[2-9]。
空間碎片環境長期演化模型可以預測未來幾十年至上百年的空間碎片環境演化,為調整太空發展戰略或制定相關空間政策提供技術支持,以保證未來太空活動可持續發展。空間碎片演化模型能夠模擬空間碎片的主要增長機制和減少機制,例如未來的航天器發射、在軌碰撞或爆炸解體、自然隕落、任務后處置等,通常由軌道預報模型、未來發射模型、碰撞概率評估模型、解體模型、任務后處置模型等幾個子模型組成。由于在軌碰撞解體是空間碎片在未來演化中的重要增長來源,對碰撞概率的評估會影響空間碎片在軌碰撞事件的預測,因此碰撞概率評估模型是空間碎片演化模型中較為關鍵的環節之一。
傳統的瞬時碰撞概率計算方法多是基于空間物體的位置橢球誤差[10-11],然而空間碎片演化模型預測的時間較長(幾十年甚至幾百年),空間物體軌道預報的精度有限,且高精度的位置誤差對于長期演化并不具有實際意義,因此傳統的瞬時碰撞概率計算方法并不適用。要預測空間碎片在未來長期演化中發生碰撞解體事件的可能性,需要一種適用于長期軌道演化系統的碰撞概率估計方法。
Cube模型是由美國國家宇航局(National aeronautics and space administration, NASA)提出的一種快速成對算法,適用于任何軌道演化系統。Cube算法通過對整個演化系統進行時間均勻采樣,能夠利用演化過程中不斷更新的軌道根數來評估空間物體之間的碰撞概率[12-13]。Cube模型算法具有原理簡單、配對快速的優點。Cube模型算法提出后,被多個國家的空間碎片環境長期演化模型所采納。但在2014年第32屆機構間空間碎片協調委員會(Inter-agency space debris coordination committee, IADC)全體會議上,法國宇航局(Centre national d’etudes spatiales, CNES)指出,利用其演化模型MEDEE模擬低地球軌道(Low earth orbit, LEO)空間環境的未來演化,當Cube模型的立方體尺寸取值不同時,空間環境演化結果會有較大差異,如圖1所示,圖中粗線表示40次蒙特卡洛運行的平均結果,細線表示1σ的標準差。表1為MEDEE模型預測的200年后的LEO空間碎片數量相比于初始碎片數量的變化百分比,及其1σ標準差[14-15]。但從物理規律而言,空間碎片在演化過程中的碰撞概率不會因碰撞概率評估算法不同而改變,因此若Cube模型因其參數設置不同而對未來空間環境演化結果帶來顯著影響,將直接導致空間碎片演化模型的可信度降低。
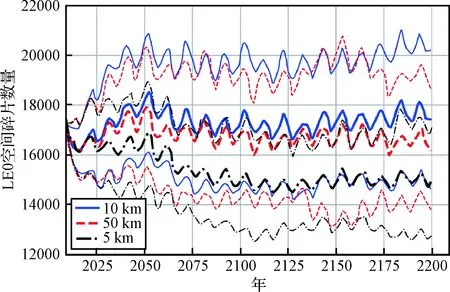
圖1 立方體大小不同時MEDEE模型的運行結果Fig.1 Evolution results of MEDEE with different cube sizes

立方體尺寸/km200年后碎片數量相比于初始碎片數量的百分比[平均值+/-1σ標準差]h=5-13%+/-12%h=102%+/-16%h=15-5.3%+/-14%
本文對此問題進行了深入分析,研究了Cube模型算法及其在空間碎片演化模型中的應用問題,并在Cube模型算法的基礎上做了改進,提出了I-Cube模型。經過多次蒙特卡洛模擬運行驗證,使用改進后的I-Cube算法,空間碎片演化模型的演化結果不再受碰撞概率算法參數的影響,顯著提高了演化模型的穩定性與可信度。
本文所使用的SOLEM模型(Space objects long-term evolution model)是我國自主建立的空間碎片長期演化模型[16-17]。SOLEM模型作為中國國家航天局(China national space administration, CNSA)的代表參與了IADC組織的多項國際聯合研究,并取得了與國際上其他演化模型較為一致的結果[18]。
本文第1部分對Cube模型算法及其在空間碎片演化模型中的應用做了進一步說明與分析,第2部分介紹改進的碰撞概率模型I-Cube,第3部分對比分析了采用Cube模型算法與I-Cube算法的演化結果,第4部分進行了總結。
1 碰撞概率模型及其對演化的影響
碰撞概率的計算直接影響空間碎片碰撞解體次數的預測。碰撞解體是未來空間碎片數量增長的重要來源,因而對空間碎片間的碰撞概率估計成為影響未來空間環境演化仿真結果的關鍵環節之一。
1.1 碰撞概率算法Cube模型
Cube模型是由NASA提出的適用于任何軌道演化系統的碰撞概率評估算法[12-13]。Cube算法通過對整個演化系統進行時間均勻采樣的方法來計算空間碎片的碰撞概率。數學上,物體i和j之間在很長一段時間內(從tbegin到tend)的總碰撞次數可表達為:
(1)
式中:Pi,j是碰撞率;L是tbegin和tend之間的時間間隔數;ts和ts+1代表第s個時間間隔的起止時刻。如果時間間隔ts+1-ts足夠短,兩個空間碎片之間的碰撞特征變化不大,那么可認為Pi,j在這段時間內是常數,則上述積分表達式可寫為
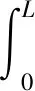
(2)
在每次采樣時刻,建立地心笛卡爾坐標系,將三維近地空間劃分成多個邊長為h的小立方體,每個空間物體的位置、速度根據該時刻的軌道根數計算。當兩個空間物體處于同一個立方體時,碰撞率Pij由下式計算
Pij=sisjAcVimpdU
(3)
式中:si和sj表示目標i和j在該立方體內的空間密度;Ac表示兩目標的碰撞截面;Vimp表示兩個目標的碰撞速度;dU表示該立方體的體積。對Pij進行時間積分后得到碰撞概率
pij=Pij·[ts+1-ts]=sisjAcVimpdUdt
(4)
計算出pij后,應用蒙特卡羅方法生成一個隨機數Ri與pij進行比較,以此來確定一次碰撞是否發生。若一個立方體內同時有兩個或多個物體,計算其兩兩之間的碰撞概率,并確定碰撞是否發生;而若一個立方體內只有一個空間物體,則不再考慮該物體與其他物體的碰撞可能性。對于N體系統,該方法能夠快速有效地找出碰撞配對物體,計算時間與N成正比,而非N2。
根據標準統計采樣方法,采樣次數越多,即采樣時間間隔越短越好,但在空間碎片長期演化模型中,需要考慮整個模型的運行速度,不能在碰撞概率計算上花費過多的時間。在美國的空間碎片長期演化模型LEGEND中,dt默認值為5天[13]。
而關于采樣時刻所劃分的立方體大小,Cube模型認為在平均軌道半長軸的1%及以內都是合理的[13]。將其應用在空間碎片演化模型中時,主要研究對象是LEO軌道的碎片,軌道半長軸在6578~8578 km之間,故依據Cube模型,其所劃分的立方體尺寸在65 km及以下時都是合理的。美國空間碎片長期演化模型LEGEND中,h取值為10 km[13]。
1.2 Cube算法存在的問題
依據Cube模型,上述碰撞概率算法式(4)相當于在一個微觀尺度上(一個立方體內)應用氣體動力學理論。然而,根據式(4)計算出的pij并非真正的碰撞概率,而是兩個物體在所劃分的立方體dU內在積分時間dt內的平均碰撞次數。在積分時間并非趨于0的情況下,對于個別截面積超大的碎片,用該式計算出的碰撞概率存在pij>1的情況。實際上,在pij≤0.2的情況下,可將其近似看作碰撞概率,其誤差小于10%,而當pij>0.2時,該近似不再成立,必須使用碰撞概率的嚴格表達式(見式(5))[19]。
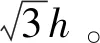
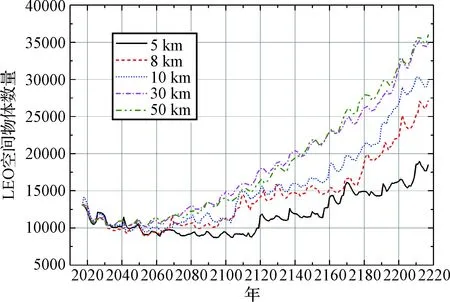
圖2 立方體大小h對空間碎片演化預測結果的影響Fig.2 Evolution results of SOLEM model with the cube size h
2 改進的碰撞概率算法I-Cube模型
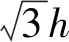
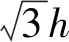
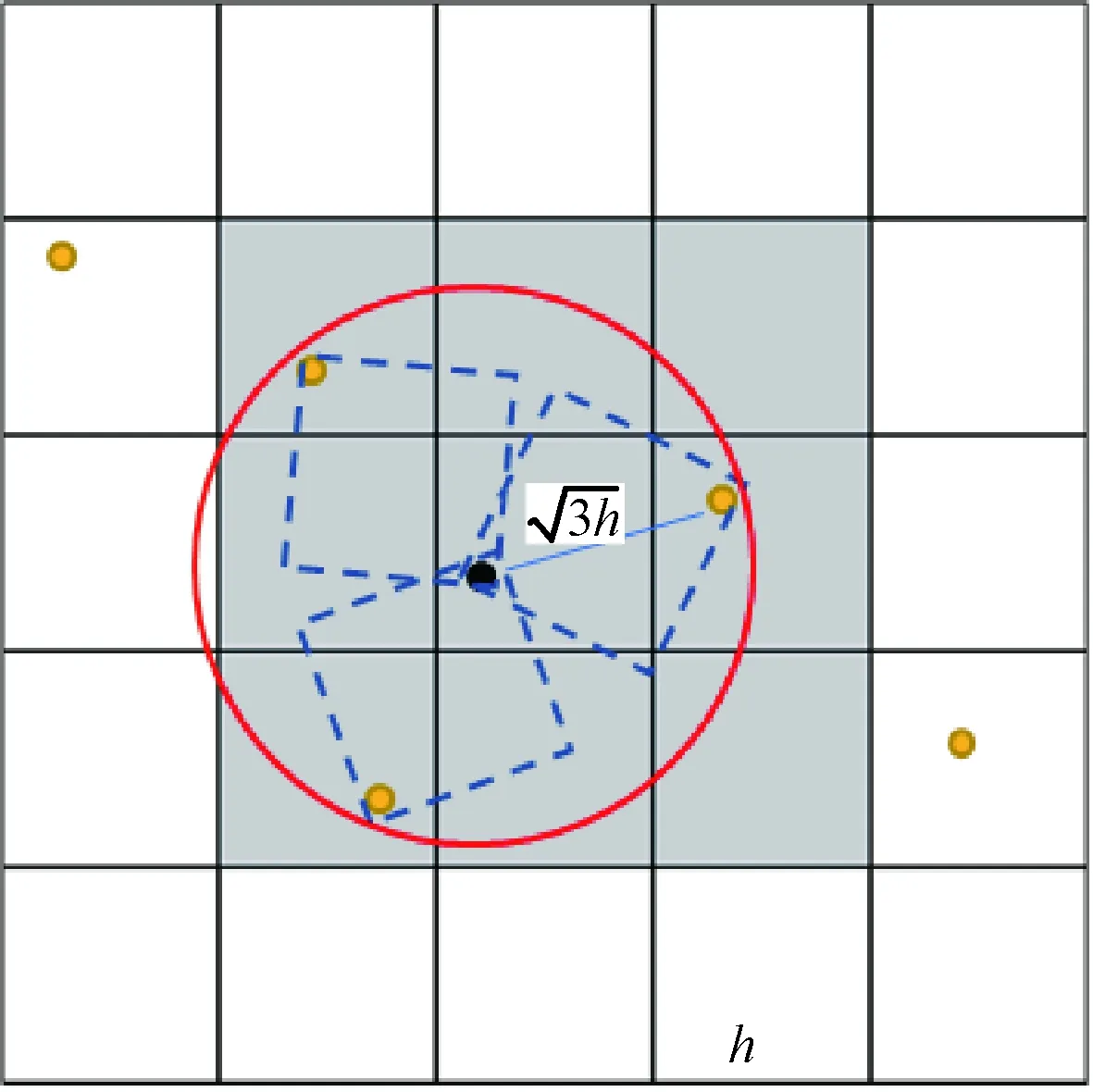
圖3 考慮相鄰立方體中兩個物體的碰撞概率的二維示意圖Fig.3 Two-dimensional representation for considering possible collisions between debris residing in neighbouring cubes
I-Cube算法的具體實現步驟如下:
1)確定對演化系統進行時間均勻采樣的間隔dt。在SOLEM模型中,時間采樣間隔dt為5天。
2)對近地空間劃分立方體。在采樣時刻,建立地心笛卡爾坐標系,將地球周圍的近地空間劃分為一個個邊長為h的立方體,并對每個立方體按h的倍數進行編號。
3)計算空間物體所在的位置。在采樣時刻,根據每個空間物體(序號為i)更新后的軌道根數計算其所在的位置,并記錄其所處的立方體編號。
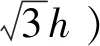
5)計算配對目標之間的碰撞概率pij。
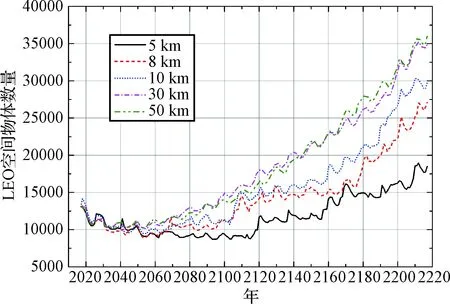
6)利用蒙特卡羅方法判斷碰撞是否實際發生。生成0~1之間的隨機數Ri,若Ri 步驟5)中碰撞概率pij的具體算法如下: 根據氣體動力學,在體元dU內,在dt時間內,空間物體i和j的平均碰撞數為 c=SiSjVimpAcdUdt (5) pij=1-exp(-c) (6) 與Cube算法相比,I-Cube算法采用了嚴格表達式來計算碰撞概率pij,此外增加了處于相鄰立方體內的空間物體間碰撞可能性的計算,尋找碰撞配對物體的復雜度增加,因而計算所用的時間也相應增加,基本相當于原Cube算法計算時間的3倍。但從整個演化模型運行上看,這個計算速度仍在可接受范圍內。 據目前公開的文獻看,只有CNES利用其MEDEE模型對原Cube算法參數的影響做過相關研究[14-15],此外,UKSA的DAMAGE模型采用Cube算法并對其做了部分改進[20]。但由于各國的空間碎片長期演化模型在各個模塊算法的具體技術實現方式并未公開,MEDEE模型、DAMAGE模型以及國際上其他長期演化模型在Cube算法的應用或改進方面,以及太陽活動、大氣模型等關鍵影響因素的假設與參數設置方面均與SOLEM模型不盡相同,且在已公開的文獻中,MEDEE和DAMAGE模型與SOLEM模型所使用的初始空間碎片數據也不同,故無法就Cube算法改進前后其參數對空間環境演化仿真的影響與SOLEM模型形成橫向對比。鑒于SOLEM模型在國際聯合研究中的出色表現,并出于避免不同演化模型因模型本身差異帶來影響的考慮,本文僅利用SOLEM模型在保證其他關鍵影響因素保持不變的前提下,對Cube算法改進前后改變參數h對演化結果的影響進行研究。 SOLEM演化模型中將太陽輻射流量和地磁活動設為平均值,即F10.7=130 sfu,Ap=9。軌道預報算法為簡化的半分析法,考慮地心引力、地球非球形引力攝動、大氣阻力攝動、第三體引力攝動和光壓攝動,大氣密度模型采用NRLMSIS00模型。碰撞解體模型采用NASA標準解體模型。以2017年9月1日的空間碎片環境數據作為初始輸入,預報200年至2217年9月1日。以2009.09.01至2017.08.31之間8年的發射情況作為發射模型在未來200年內不斷循環,航天器任務壽命假設為8年,不考慮軌道維持和人工避碰措施,任務后軌道處置率假設為30%。 SOLEM模型在上述假設條件均不變的情況下,碰撞概率評估模型分別采用Cube算法和I-Cube算法,僅改變參數h的大小,研究其對未來200年空間碎片環境演化的影響。本文算例中參數h取值分別為5 km、8 km、10 km、30 km、50 km。每個算例均運行50次蒙特卡洛模擬并求平均。仿真結果如圖4~圖7所示,其結果量化如表2所示。 圖4 采用Cube算法,未來空間碎片數量的演化Fig.4 Predictions of future space environment evolution using Cube method 圖5 采用I-Cube算法,未來空間碎片數量的演化Fig.5 Predictions of future space environment evolution using I-Cube method 圖6 采用Cube算法,未來200年空間碎片碰撞次數的預測Fig.6 Predictions of cumulative number of space debris collisions in future 200 years using Cube method 圖4~圖7以及表2所示的仿真結果表明,演化模型在其他如太陽輻射等關鍵影響因素保持不變的情況下,采用原Cube算法,改變所劃分立方體的大小h會嚴重影響未來空間碎片環境的演化結果。就算例中h的取值范圍(5~50 km),不同的取值造成200年后空間碎片數量演化的預測值相差約17500個,為2017年初始碎片數量的134%;200年累計災難性碰撞次數預測相差23次,非災難性碰撞次數預測相差約27次。由于h的取值皆在“平均軌道半長軸的1%及以內”的合理范圍,因而無法判斷哪種演化結果可信。 而采用I-Cube算法后,改變參數h大小,未來空間碎片環境的演化結果不再受其顯著影響。就算例中h的取值范圍(5~50 km),不同的取值造成200年后空間碎片數量演化的預測值相差僅為2017年初始碎片數量的18%,200年累計災難性碰撞次數預測相差不到4次,非災難性碰撞次數預測相差約6次。 圖7 采用I-Cube算法,未來200年空間碎片碰撞次數的預測Fig.7 Predictions of cumulative numbers of space debris collisions in future 200 years using I-Cube method 由此可見,采用I-Cube算法后,未來空間碎片的演化結果高度一致,碰撞解體事件的預測不再受參數h的顯著影響。相比于采用Cube算法,I-Cube算法對碰撞概率的計算更為準確合理,進而使空間碎片演化模型的穩定性與可信度顯著提升。 I-Cube算法采用了嚴格表達式來計算空間物體間的碰撞概率,排除了原Cube算法中可能出現“碰撞概率”大于1的隱患。 I-Cube算法與Cube算法的模型假設不同。I-Cube算法假設只要兩個物體間的距離在給定閾值范圍內都存在碰撞可能性,而Cube算法假設只有位于同一個立方體內的物體之間存在碰撞可能性。相比之下,I-Cube算法的模型假設更符合物理真實。 I-Cube算法保留原Cube算法尋找碰撞配對物體的思路,仍通過在采樣時刻對近地空間劃分立方體的方法來快速尋找潛在的碰撞對,但尋找潛在碰撞對的范圍由原來的同一立方體擴展至相鄰的立方體。由于增加了尋找碰撞配對物體的復雜度,I-Cube算法犧牲了一部分計算時間,但從空間碎片演化模型的整體運行上看,計算速度仍可接受。 表2 采用Cube算法與I-Cube算法,改變參數h對未來空間環境演化的影響對比Table 2 Impacts of varying parameter values of h on the predictions of future space debris environment evolution using Cube algorithm compared with those using I-Cube algorithm 相比于Cube算法,I-Cube算法提升了碰撞概率計算方法的準確度與合理性,使空間碎片環境長期演化模型的演化結果不再受自身碰撞概率算法參數的影響,從而提高了空間碎片長期演化模型的穩定性與可信度。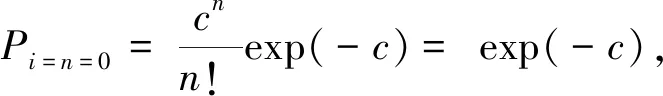
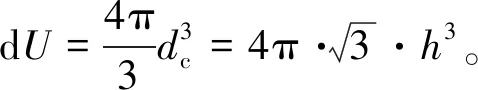
3 仿真分析

4 結 論