基于差分方程的高溫防護服溫度分布研究
2019-05-10 09:52:54何玉華北水利水電大學數學與統計學院金融數學專業
數碼世界 2019年4期
何玉 華北水利水電大學數學與統計學院金融數學專業
引言
隨著現代化社會的迅猛發展,各個的產業領域也相繼出現各種類型的工作環境,在工業化突飛猛進的情況下,高溫作業需求隨著現代化的發展在不斷的增多。然而,高溫環境下的熱應激問題已經變得愈來愈為嚴重,很多人們也漸漸的都不愿意進行高溫作業。高溫作業,指在高氣溫或有強烈的熱輻射、或伴有高氣濕相結合的異常氣象條件下的作業。在現實的生產生活中,總會不可避免的存在著高溫作業,而高溫作業往往對人體的傷害是巨大的,怎樣在高溫環境下保持較長時間的工作并且絕對保證作業人員的安全成為社會上一個日趨迫切解決的問題。
1 熱傳導差分方程建立
假設溫度在傳播時均勻傳播,在某一時刻,測量假體任意位置的溫度相同。由題可知:密度是、比熱是、熱傳導率是、熱傳導系數是k。取x軸與高溫服裝厚度重合,以u(x,t)表示x點在t時刻溫度,則有:
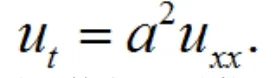
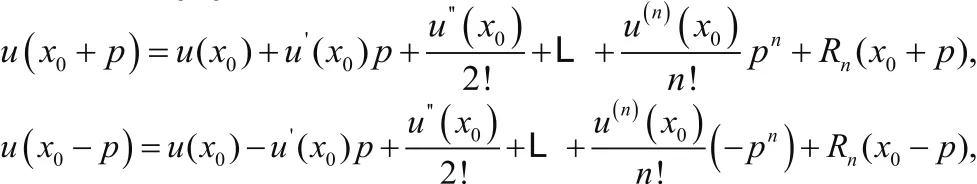
聯立上述兩式,可得:
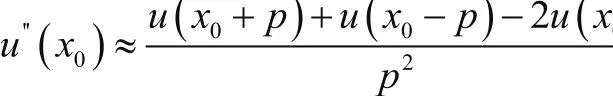
將溫度在點(x0,t0)沿t方向進行距離為φ展開為泰勒級數,可得:
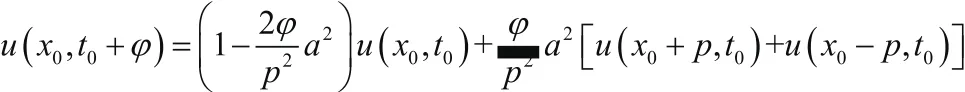
由此上式為所求熱傳導差分方程。
2 模型求解
已知高溫服裝有三層織物材料和一層空氣層構成,記為I、II、III、IV層,建立差分方程模型,分別求解I、II、III、IV層溫度分布。由條件帶入可得邊界條件為:
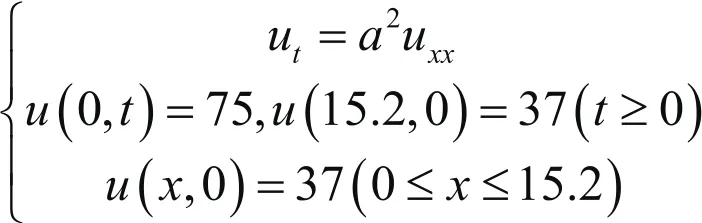
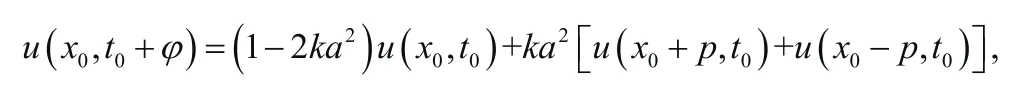
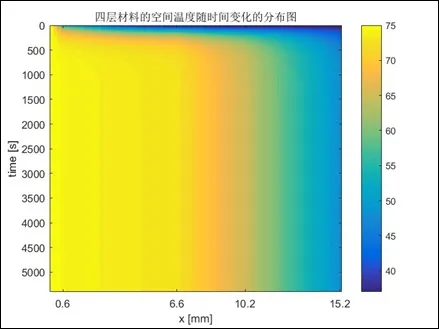
利用有限差分可得到四層穩態時的溫度分布數值解,即各層穩態溫度為下表。

表1 各層穩態溫度
3 結論
在現實的生產生活中,總會不可避免的存在著高溫作業,而高溫作業往往對人體的傷害是巨大的,怎樣在高溫環境下保持較長時間的工作并且絕對保證作業人員的安全成為社會上一個日趨迫切解決的問題。本文由此建立的高溫防護服一維熱傳遞模型,使用差分方程的方法,能夠有效利用數據,在取較小步長的情況下,得到四層不同物質在傳遞中每秒的溫度改變,實現熱傳遞的動態演示。
猜你喜歡
新作文·小學低年級版(2021年9期)2021-11-27 07:57:46
中老年保健(2021年12期)2021-08-24 03:30:40
中國傳媒大學學報(自然科學版)(2021年1期)2021-06-09 08:43:00
學生天地(2020年17期)2020-08-25 09:28:54
少年博覽·初中版(2020年6期)2020-06-12 11:42:23
中國生殖健康(2020年6期)2020-02-01 06:28:50
新世紀智能(英語備考)(2019年12期)2020-01-13 06:07:18
中國生殖健康(2019年11期)2019-01-07 01:28:02
中國生殖健康(2018年6期)2018-11-06 07:09:28
故事大王(2016年7期)2016-09-22 17:30:08

