水合物法捕集煙氣中CO2的新擬合熱力學模型

李璐伶 趙金洲 李海濤 張烈輝 樊栓獅,2 李清平龐維新 呂 鑫 鄭利軍 魏 納

1.“油氣藏地質及開發工程”國家重點實驗室·西南石油大學 2.華南理工大學傳熱強化與過程節能教育部重點實驗室3.中海油研究總院有限責任公司

0 引言

火電廠所排放煙氣中含有大量的CO2，約占CO2總排放量的75%[1-2]。CO2是一種對環境有害的溫室氣體，但同時也是一種寶貴的資源[3-4]。因此，有必要捕集煙氣中的CO2。常用CO2捕集工藝包括化學吸收法[5-6]、物理吸收法[7-10]、膜分離法[11]以及低溫分離法[12]。低溫分離法中的水合物法[12]因能耗低、操作簡便，有利于后續CO2儲存、利用等特點，被認為是最具前景的CO2捕集工藝之一[13-15]。

為了滿足CO2捕集要求，需要多級水合反應。各級水合反應操作條件的確定須利用熱力學模型，因此，為了降低多級反應所累積的總誤差，準確的熱力學模型顯得尤為重要。熱力學模型的建立是基于體系達平衡時，同一物質在各相的化學位之差或逸度相等的原理。常用的氣液模型主要包括SRK方程、PR方程、CPA方程、SAFT方程以及DA方程，水合物相模型主要包括vdW-P模型[16]與Chen-Guo模型。

Herslund等[17]利用vdW-P+CPA模型計算CO2—N2生成水合物的相平衡壓力，發現針對低濃度CO2煙道氣，誤差較大。Zhang等[18]對vdW-P+PR模型進行修正，用于預測CO2—N2在促進劑作用下生成水合物的相平衡條件。結果顯示，該模型在已知溫度預測生成壓力時，準確度較低。Herri等[19]基于vdW-P+SRK模型，并利用3種方法計算Langmuir吸收系數，結果發現計算煙氣相平衡壓力的平均絕對誤差均高于8%。綜上所述，目前所建立的熱力學模型準確度還有待提高[20]。為此，筆者針對vdW-P+CPA模型修正，并驗證其準確性。

1 熱力學模型

1.1 氣液相模型

CPA方程中剩余摩爾Helmholtz自由能項（Ares）的微擾展開式如下[21]：

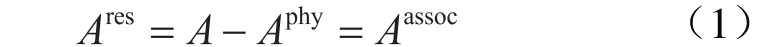
其中

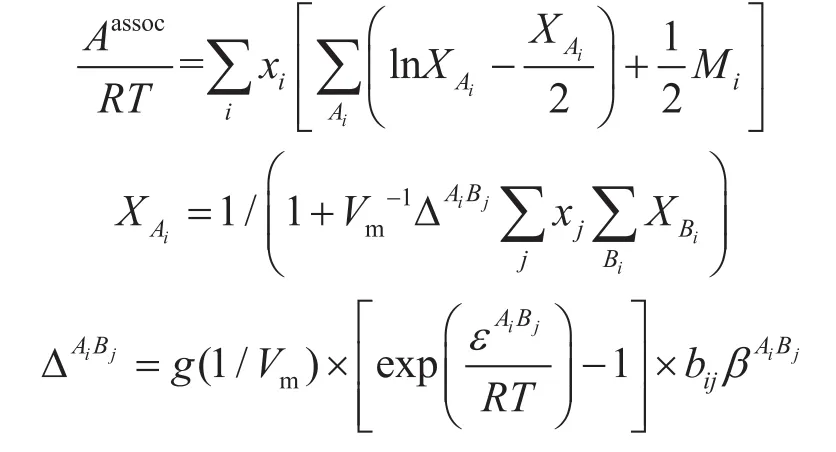
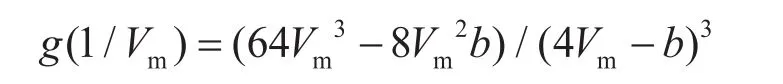
式中A表示總的Helmholtz自由能，J/mol；Aphy表示物理項的Helmholtz自由能，J/mol，筆者利用SRK方程計算；Aassoc表示締合項的Helmholtz自由能，J/mol；R表示通用氣體常數，R=8.314 J/(mol·K)；T表示溫度，K；xi表示i組分的摩爾分數；Ai表示i組分的締合位A；Mi表示i組分締合位個數；XAi表示i分子上A配位未被占據的摩爾分數；Vm表示摩爾體積，m3/mol；XBi表示i分子上B配位未被占據的摩爾分數；ΔAiBj表示i分子的A配位與j分子的B配位締合強度，m3/mol；βAiBj表示能量參數；b表示體積參數，m3/mol；εAiBj表示締合體積，(Pa·m3)/mol；g（1/Vm）表示徑向分布函數。

1.2 水合物相模型

vdW-P模型中水合物相與空水合物相化學位差（Δμw,H）可由下式計算：

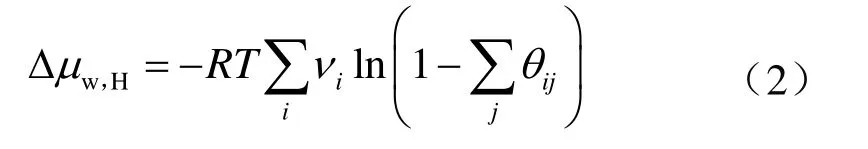
其中

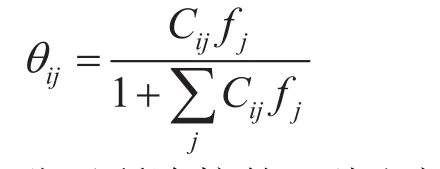
式中 表示單一水分子所連接的i型孔穴數；θij表示客體分子j在i型孔穴中的占有率；fj表示客體分子j的逸度，Pa；Cij表示客體分子j在i型孔穴的Langmuir吸收系數。

Parrish和Prausnitz[22]提出了Langmuir吸收系數的計算公式如下：

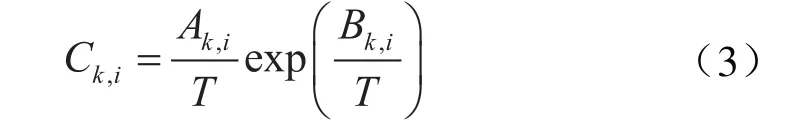
式中Ak,i、Bk,i分別表示擬合參數。

同時，Saito等[23]提出水在液相中化學位差Δμw,L的計算方法如下：

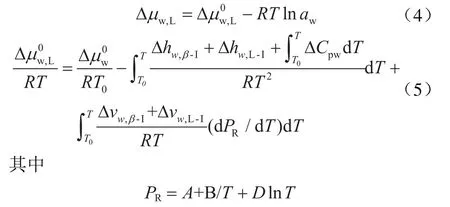
2 模型參數的擬合

本文參考文獻[17, 24]報道的CPA方程中，僅考慮了水分子間的相互締合作用，認為CO2、N2為無締合分子。而Tsivintzelis等[25]對比發現，當CO2為溶劑分子，且有一個僅能與H2O分子締合的接受電子位時，準確度較高。因此，為提高熱力學模型的準確度，筆者認為H2O為4C連接分子，CO2分子為有一個電子接受位的溶劑分子，N2為無締合分子。在此基礎上，對模型參數進行重新擬合。

2.1 能量參數α

文獻中報道的CPA方程認為CO2為無締合作用的非極性分子，直接利用CO2的絕對溫度、絕對壓力以及偏心因子計算能量參數α。同時，認為H2O為4C型分子，其能量參數α0.5為[1－（T/Tc）0.5]的一次函數。而Mathias等[26]報道過，對于極性組分其能量參數α0.5為[1－（T/Tc）0.5]的三次函數時，計算結果更為準確，而對于有分子間相互締合作用的非極性分子，能量參數α0.5為[1－（T/Tc）0.5]的一次函數時，計算結果更準確。因此，筆者利用DIPPR數據庫[27]中的CO2與H2O的飽和液相密度及飽和蒸汽壓數據，對CPA方程中的能量參數α進行回歸。基于matlab進行最優計算，目標函數可由下式計算：

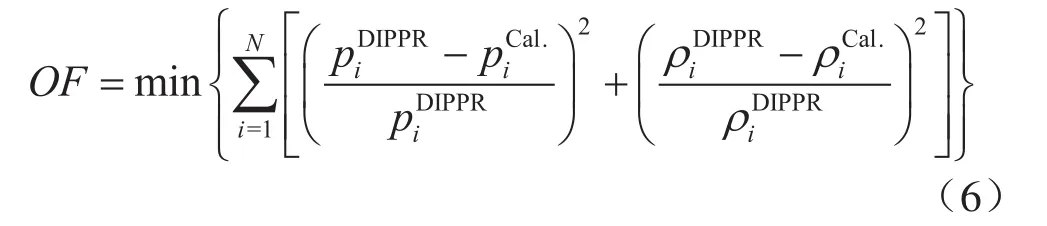
式中pi表示第i組的系統壓力，Pa；ρi表示第i組的飽和液相密度，kmol/m3；上標DIPPR表示來自DIPPR數據庫的實驗數據；上標Cal.表示模型計算值；N表示共有N組數據。

擬合得H2O與CO2的能量參數α分別表示為：

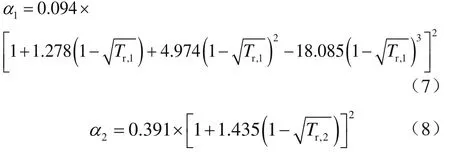
式中α1表示H2O的能量參數，Pa/（m6·mol2）；α2表示 CO2的能量參數，Pa/（m6·mol2）；Tr,1表示 H2O的對比溫度；Tr,2表示CO2的對比溫度。

為了驗證擬合結果準確性，分別利用新擬合能量參數與原能量參數[28]計算CO2與H2O的液相飽和密度，并與DIPPR數據對比，結果如圖1所示。值得注意的是，選作驗證模型準確性的實驗數據均未用于參數擬合。

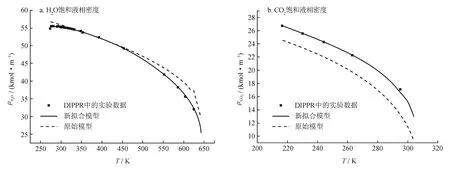
圖1 原始模型與新擬合模型計算H2O與CO2飽和液相密度對比圖

如圖1所示，兩模型均能較好地描述H2O與CO2的飽和液相密度與溫度的關系。對于H2O而言，當溫度大于420 K或小于320 K時，由于水分子極性作用對飽和液相密度的影響越來越明顯，原始模型的準確度下降。而新擬合模型在考察范圍內準確度均較高，尤其是在低溫條件下。對于CO2而言，由于原始模型認為其為無締合作用的非極性分子，直接利用絕對溫度、絕對壓力以及偏心因子計算其能量參數，導致其在低溫下的飽和液相密度與實驗值偏差較大。而筆者將CO2的α0.5擬合為[1－（T/Tc）0.5]的一次函數，計算結果準確度較高。當溫度較高時，新擬合模型的計算結果略高于實驗值，而原始模型的結果更接近實驗值。原因可能是高溫下，CO2的締合作用變弱，此時認為CO2是無締合作用的非極性分子更合理。但水合物體系為低溫體系，因此新擬合模型更適用。

為了便于對比，利用式（15）計算平均絕對誤差 (Average Absolute Deviation，AAD)。結果顯示，針對H2O而言，新擬合模型的AAD僅為0.08%，原始模型的AAD為1.84%；針對CO2而言，兩模型的AAD分別為2.09%、4.06%。綜上可知，新擬合模型在預測H2O和CO2的飽和液相密度時，準確度更高，且更適用于低溫體系，即

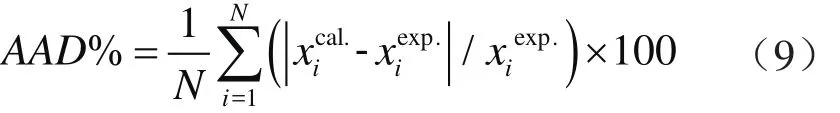
式中xi表示體系i組分的摩爾含量；上標exp.表示文獻報道的實驗數據。

2.2 二元交互作用參數kij

二元交互作用參數kij反映了不同分子間相互作用對體系熱力學性質的影響，Ruff i ne等[29]通過實驗發現，kij受溫度的影響較大。因此，利用以溫度為函數的kij，有助于提高模型計算的準確度。針對CO2—H2O體系以及N2—H2O體系的kij擬合、驗證過程在前期工作中有詳細描述[30]，在此不做贅述，擬合結果為：

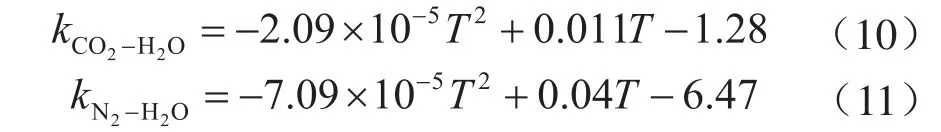
由于CO2與N2分子間作用較小，取為0[17]。

2.3 Langmuir吸附系數計算參數

Langmuir吸收系數通常是利用純氣體生成水合物的相平衡條件基于熱力學模型擬合。因此，當氣液相模型改變時，Langmuir吸收系數也應改變。如何同時確定大孔和小孔的Langmuir吸收系數是計算的關鍵。由于CO2—N2混合氣體生成水合物時，CO2大部分存在于大孔中，而N2在大小孔里均有。因此，認為CO2的小孔Langmuir吸收系數很小，大孔Langmuir吸收系數較大，N2則認為大小孔的吸收系數接近。為了簡化計算過程認為CO2與N2的小孔Langmuir吸收系數改變很小，利用純氣體生成水合物的相平衡條件[31-35]，擬合了大孔的吸收系數，并利用擬合結果求得參數，結果如表1所示。

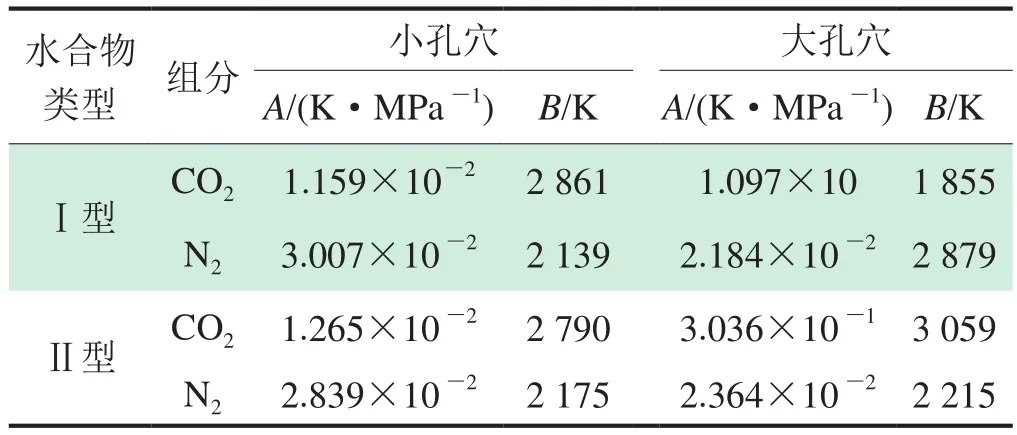
表1 式（8）的參數表

為了驗證擬合結果的準確性，將擬合參數帶入熱力學模型，分別計算純CO2與N2的相平衡條件，并與文獻報道的實驗數據進行對比，結果如圖2所示。

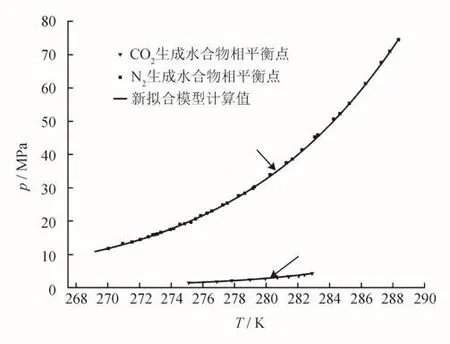
圖2 純CO2、純N2相平衡條件新擬合模型計算值與文獻報道的實驗數據對比圖

如圖2所示，隨著溫度的升高，CO2與N2生成水合物的相平衡壓力均呈上升趨勢。相同溫度下N2生成水合物的相平衡壓力明顯高于CO2，這再次驗證了利用水合物法可實現CO2與N2分離。利用本文擬合的參數計算Langmuir吸收系數，模型計算結果與文獻報道的實驗結果吻合度較高。經計算得知，模型在預測CO2與N2生成水合物的相平衡壓力時，AAD分別為0.86%和0.82%。由此可知，本論文擬合的用于Langmuir吸收系數的參數能夠保證vdW-P模型計算純物質水合物相熱力學性質的準確性。

3 模型驗證

為了驗證所建立的熱力學模型的準確性，分別利用新建模型、文獻模型[16]，計算給定溫度下煙氣生成水合物的相平衡壓力，并與文獻報道的實驗數據[32,36-37]對比。由于文獻報道實驗數據均未對進料液體分率進行報道，同時進料液體分率對相平衡條件的計算結果影響較小，結合相關文獻報道[38-39]，假設進料液體分率為0.5，計算結果如圖3所示。

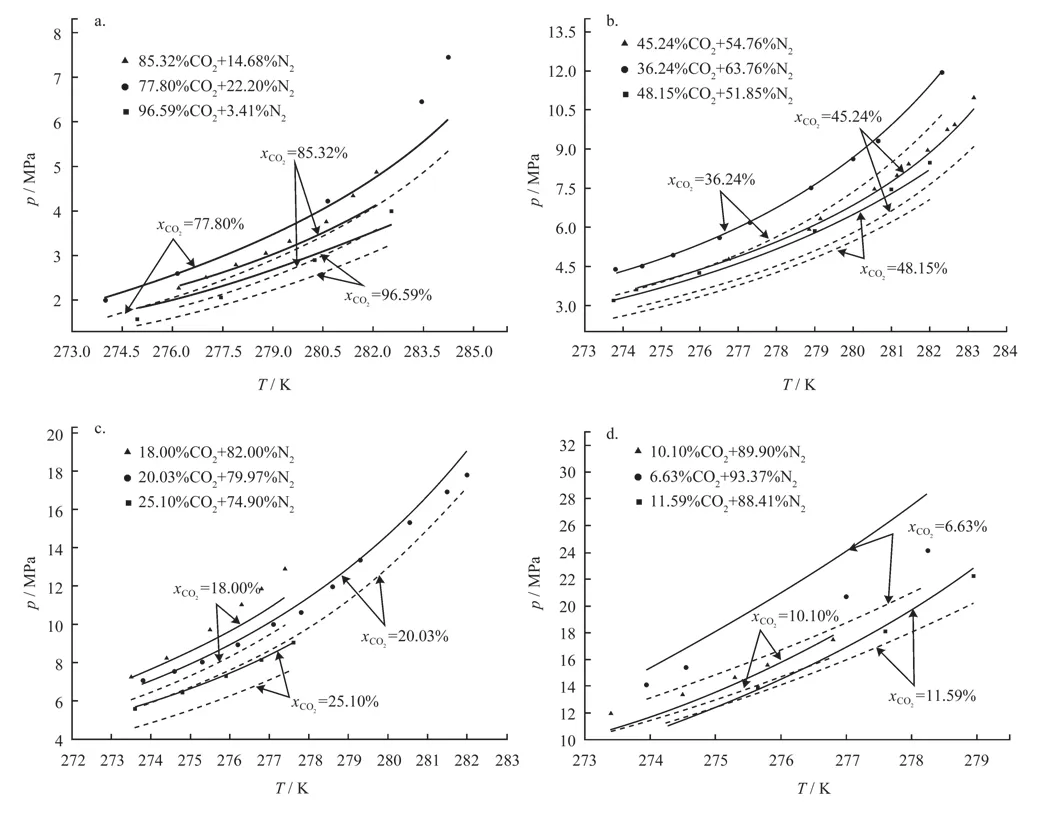
圖3 CO2+N2混合氣體生成水合物的相平衡條件的兩種模型計算值與實驗值對比圖

如圖3所示，兩模型均能很好地描述煙氣生成水合物相平衡壓力與溫度的關系。通過考慮CO2與H2O分子間的相互締合作用，并重新擬合CPA方程中的α、kij以及vdW-P模型中Langmuir吸收系數的計算參數，新擬合模型在計算煙氣生成水合物相平衡條件時的準確度較原有模型有所提高。針對大部分氣樣，尤其是CO2含量為50%左右的氣樣，新擬合模型的計算結果與實驗值的偏差受溫度影響作用較小，原因可能是與溫度相關的二元交互作用參數降低了溫度對計算結果準確度的影響。同時，通過考慮CO2與H2O分子間的相互締合作用，提高了計算氣液相組成計算的準確度。分別計算兩模型的AAD，結果如表2所示。

如表2所示，新擬合模型較文獻模型AAD的平均值由15.16%降至5.02%。但針對CO2含量為6.63%的混合氣體，新擬合模型的AAD高于文獻模型。可能原因是新擬合模型高估了N2的存在對混合氣體生成水合物相平衡條件的影響，導致當CO2含量較低時，模型的準確度下降。文獻模型針對混合氣體生成Ⅰ型水合物時的相平衡條件預測結果偏差較大，而針對Ⅱ型水合物的偏差較小。當CO2濃度大于75%時，新擬合模型的AAD相對較大，為10%～5%。可能原因是在該條件下，混合氣體生成Ⅰ型水合物，N2因壓力作用占據512小孔穴，而CO2濃度較大、分壓較大，因壓力作用會與N2競爭占據512小孔穴，而模型忽略了N2與CO2分子間的相互作用，導致準確度有輕微下降。而隨著CO2含量的減少，CO2的分壓降低，兩分子間競爭作用減弱，AAD下降。尤其是針對CO2含量為20%～48%的混合氣體，AAD約為2%。值得注意的是，當CO2含量為18%左右時，兩模型的AAD均較大，導致這個現象的原因可能是混合氣體生成水合物由Ⅰ型過渡到Ⅱ型是循序漸進的過程，而筆者將15%的CO2濃度作為界線，導致模型計算準確度下降。但總之，筆者新擬合的模型計算準確度有一定程度的提高，特別是針對CO2濃度為25.1%～48.15%的混合氣體，計算精度較高。

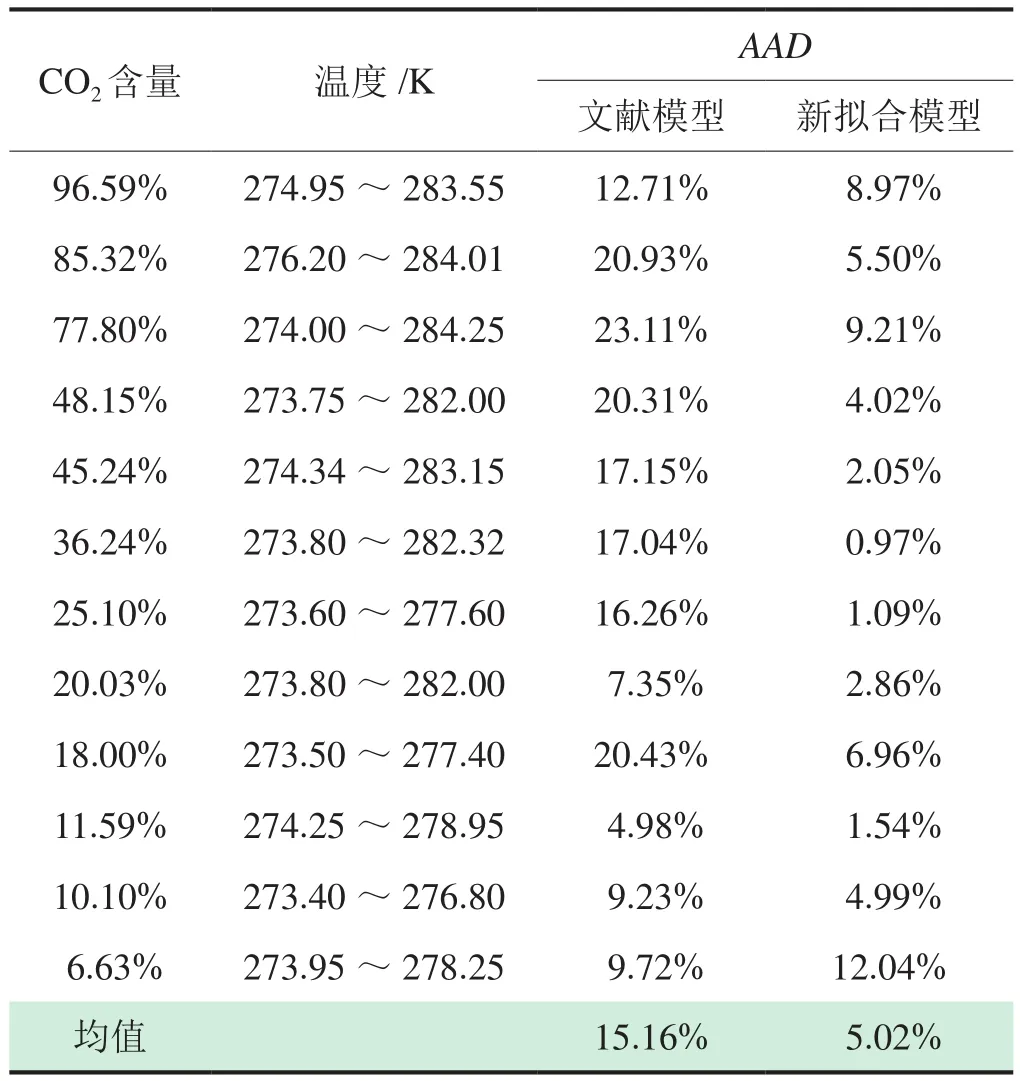
表2 文獻模型和新擬合模型的AAD計算結果對比表

4 結論

1）通過將H2O與CO2的能量參數α0.5分別擬合為[1－（T/Tc）0.5]的三次函數、一次函數，結果顯示在預測飽和液相密度時，AAD分別由1.84%下降至0.08%，由4.06%下降至2.09%。

2）在此基礎上，對vdW-P模型中Langmuir吸收系數的計算參數進行了重新擬合，經驗證，新擬合模型在預測純CO2與純N2生成水合物的相平衡壓力時，AAD僅分別為0.86%與0.82%。

3）利用新擬合模型與文獻模型分別計算不同組成煙氣生成水合物的相平衡條件，并與實驗數據對比。發現新擬合模型的準確度較文獻模型有了較大程度地提高，AAD由15.16%降至5.02%。特別是針對CO2濃度為25.1%～48.15%的混合氣體，新擬合模型計算精度較高。

4）針對CO2濃度為18%的煙氣，兩模型計算結果均存在較大誤差，原因是氣體生成水合物由Ⅰ型過渡到Ⅱ型是循序漸進的過程，而本文將CO2含量為15%作為界線，導致在該范圍的計算精度下降。

總之，通過考慮CO2與H2O分子間的相互締合作用，對原有模型進行修正，所建立的新擬合模型的準確度有一定程度提高，為水合物法的實際應用提供參考作用。