基于改進蟻群算法的移動機器人平滑路徑規劃

孫 瑞，張文勝

?

基于改進蟻群算法的移動機器人平滑路徑規劃

孫 瑞，張文勝

(石家莊鐵道大學交通運輸學院，河北 石家莊 050043)

針對移動機器人提出了基于改進蟻群算法的平滑路徑規劃方法。為了克服蟻群算法解決路徑規劃問題時存在的收斂速度慢的缺點，對啟發因子的矩陣初始值及更新方式進行了改進，啟發因子改進后的結果與之前相比，平均路徑長度減少了17.6%，平均收斂代數減少了93.1%；對于柵格環境下存在障礙物時機器人累計轉彎角度大的問題，提出了控制點轉移策略，在上一步改進的基礎上，通過對控制路徑走向的柵格中心點向柵格角頂點的轉移，實現了路徑規劃的平滑改進。路徑規劃仿真結果表明，與平滑改進前相比，平滑改進后機器人的平均路徑長度減少了4.28%，累計轉彎角度減少了52.58%。

蟻群算法；移動機器人；路徑規劃；控制點轉移策略

隨著人工智能的發展，機器人在人類社會發揮著越來越重要的作用[1]。移動機器人的路徑規劃是機器人執行任務的首要條件[2]，可要求機器人在躲避障礙物的前提下，找到從出發點到目的地的最優路徑。

蟻群算法是模仿自然界中螞蟻覓食過程發展起來的一種優化方法[3-4]，具有較強的魯棒性，在解決優化問題方面顯示出巨大優勢和發展潛力[5-7]，廣泛應用于移動機器人路徑規劃問題。目前眾多學者對其進行研究，徐勝華等[8]在解決機器人路徑規劃問題時對蟻群算法進行改進，使其能根據環境特征進行優化；張文強和張彥[9]提出一種改進蟻群算法，將引力系數和避障系數引入啟發因子中，提高了解的質量和搜索效率；朱艷等[10]將方向信息加到啟發因子中，且動態調整權重系數使算法搜索效率更高；王輝等[11]通過更改啟發因子及信息素更新規則，使改進后的算法收斂更快；王志中[12]提出了螞蟻相遇策略及螞蟻回退策略，設置了信息素感應閾值，對信息素殘留方法進行了改進，使改進后的蟻群算法具有更快的收斂速度以及更優的規劃結果；張瑋等[13]采用改進煙花-蟻群混合算法進行最優路徑的求解，將改進煙花算法得到的最短路徑作為參照路徑，將其換算成蟻群算法的初始信息素分布，結果表明該算法具有良好的性能；王紅君等[14]提出了一種平滑蟻群算法，將路徑上當前節點與其他不在同一條直線上的節點依次連線，如果新的連接線不穿越障礙物，則將當前連接線作為新路徑代替原來路徑，降低了路徑長度。

以上研究大多是對蟻群算法進行改進，對于改進后的路徑進行平滑的方法較少。本文不但通過改進啟發因子實現了對蟻群算法的改進，而且提出了控制點轉移策略，通過對控制路徑走向的柵格中心點向柵格角頂點的轉移，實現了對蟻群算法改進后的路徑平滑操作，為蟻群算法的改進及路徑平滑操作提供了一種新思路。

1 環境建模

柵格法可使機器人感知的柵格信息與環境相對應，且柵格法地圖易于創建和維護，因此采用柵格法建立移動機器人二維空間環境模型。柵格法模型如圖1所示，劃分柵格區域的指標為機器人單位運動步長。左上角柵格為起始柵格，柵格序號按自左向右，從上至下的順序依次增大，右下角柵格為終點柵格。障礙物柵格表現為黑色，自由柵格為白色[15]。設為柵格序號；為柵格的邊長。柵格序號與柵格中心點坐標對應關系如下

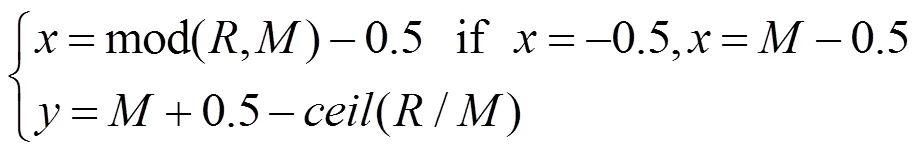
2 基本蟻群算法

在覓食過程中，螞蟻根據信息素濃度選擇新的路徑，并賦予路徑一定概率。信息素具有揮發性，隨著時間的推移，揮發留下的信息素能引導螞蟻找到最優路徑[16-17]。

在尋找新的食物源時，螞蟻沒有信息素指引，因此進行完全隨機搜索，此時所有路徑均被賦予相同的概率。螞蟻將更多的信息素留在較短的路徑上，較長的路徑逐漸被放棄[18]。之后會有更多的螞蟻選擇信息素較多的路徑，這就形成了正反饋機制，通過該機制，蟻群中螞蟻能沿著最佳路徑找到食物。該過程如圖2所示。

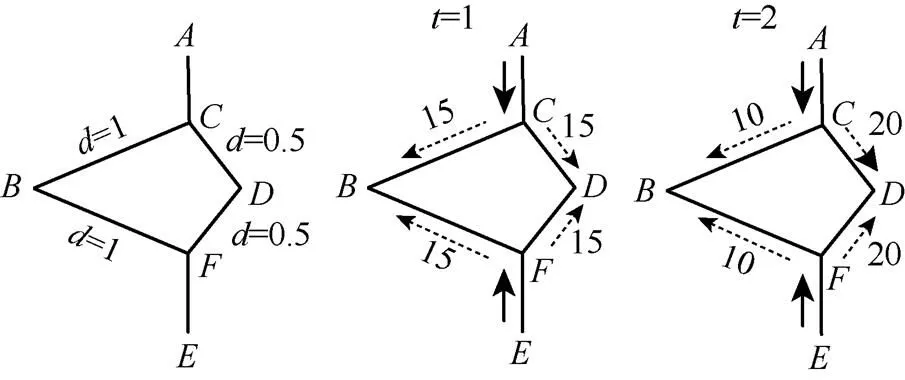
圖2 螞蟻覓食示意圖

設為食物來源；為蟻巢所在地；為時間；和為單位距離；和為0.5單位距離。設和中有30只螞蟻，當＝1時，上沒有信息素，因此螞蟻以相同的概率選擇路徑。經過1單位時間后，路徑上信息素量是的2倍；當＝2時，和中的30只螞蟻根據先前迭代中不同路徑上的信息素濃度再次選擇路徑：從點出發的螞蟻有20只選擇，10只選擇；從點出發的螞蟻有20只選擇，10只選擇，因此，較短路徑上積累了更多的信息素。隨著時間的推移，會有更多螞蟻選擇()路徑，直到最后一組螞蟻均找到蟻巢和食物之間的最短路徑。螞蟻覓食是一個正反饋過程。某刻，螞蟻從節點轉向節點的概率為[19]

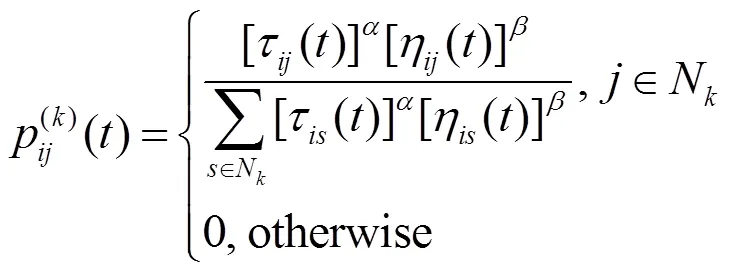
3 改進蟻群算法

3.1 啟發因子的改進

對于啟發因子的改進分為啟發因子矩陣初始值和啟發因子更新方式2部分。

3.1.1 啟發因子矩陣初始值的改進

在基本蟻群算法中，啟發因子矩陣初始值為該節點與下一節點距離的倒數。經驗證其收斂性能較弱、全局搜索能力較差。為加強蟻群算法收斂性能，減少收斂代數，提高全局搜索能力，對啟發因子矩陣初始值進行改進，即

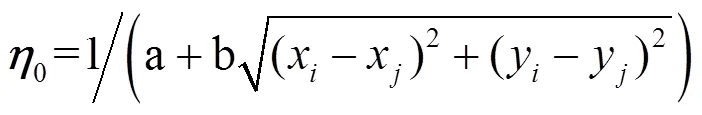
(x,y)為該節點處坐標值，(x,y)為下一節點處坐標值，引入常數a、b，使啟發因子矩陣初始值為任意兩節點距離進行初等變換后的倒數。在第4節中進行路徑規劃統計結果分析，找到移動機器人路徑規劃最短且收斂代數最少的a、b值。

3.1.2 啟發因子更新方式的改進

在基本蟻群算法中，啟發因子為該節點與下一節點距離的倒數，使螞蟻具有一定的盲目性，易陷入局部最優而錯失全局最優路徑[20]。為減少這種情況的發生，提高蟻群算法全局搜索能力，引入下一節點到目標節點之間的距離，對啟發因子更新方式進行改進，即

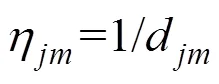
其中，為下一節點；為目標節點；d為節點到目標節點之間的距離。

將改進后啟發因子帶入狀態轉移公式，得到改進后的狀態轉移公式為

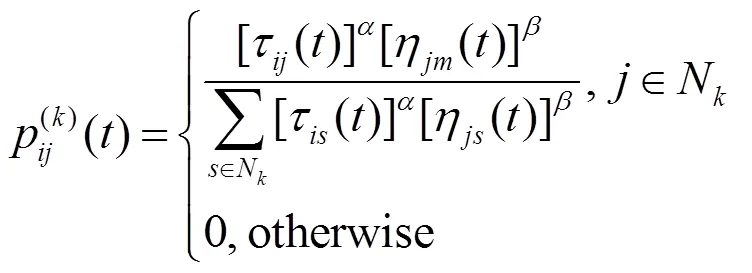
分析可知，當下一節點到目標節點之間的距離越大時，啟發因子越小，螞蟻選擇該節點的概率隨之越小。也就是說，當搜索到的距離越短時，螞蟻選擇的概率越大，因此移動機器人路徑規劃更優。

3.2 路徑規劃的平滑改進

在柵格環境下，移動機器人的路徑規劃是該路徑上各個柵格中心點連成的直線段，將這些柵格中心點稱為控制點，其控制著移動機器人的路徑規劃。由于移動機器人的路徑是從中心點到中心點的直線段，從一定程度上增加了路徑長度，且增大了移動機器人累計轉彎角度。對路徑規劃進行平滑改進，不僅能減少移動機器人運行距離，還能降低其由于轉彎帶來的能耗[21]。

圖3實線為基于蟻群算法搜索到的路徑，從點到點的路徑由3段折線組成。若將路徑上的點與點相連，能減小移動機器人路徑規劃累計轉彎角度，且根據三角形兩邊之和大于第三邊的定理，線段的長度小于原路徑長度。

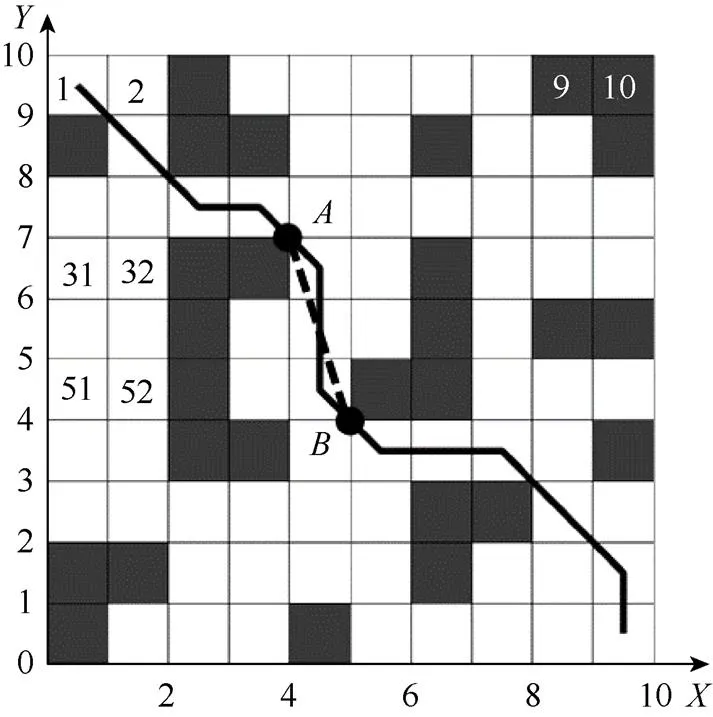
圖3 從A到B的路徑規劃改進

因此引入控制點轉移策略，將圖3中第35個柵格的控制點由柵格中心點轉移到該柵格上離起點最近的點，將第55個柵格的控制點由柵格中心點轉移到該柵格上離終點最近的點，刪除原路徑上第45個柵格的中心點，并將點與點連接成一條直線段。因此，縮短了路徑規劃的距離，減少了路徑規劃的累計轉彎角度，實現了路徑的平滑操作。

3.3 基于改進蟻群算法的移動機器人平滑路徑規劃

步驟1.運用經過啟發因子改進后的蟻群算法生成一條機器人最優路徑。

步驟2. 引入控制點轉移策略，即通過對控制路徑走向的柵格中心點向柵格角頂點的轉移，進行路徑簡化與平滑操作。

設置路徑起點為，終點為。控制點轉移策略主要針對除起點與終點之外的路徑上的其他柵格中心點。當路徑上存在豎直線段時，將最上方柵格中心點記為(X,Y)，分別判斷所在柵格的4個角頂點：U(X–0.5,Y+0.5)，U(X+0.5,Y+0.5)，U(X+0.5,Y–0.5)，U(X–0.5,Y–0.5)與起點的距離，選擇與起點的距離最小的點作為轉移的目標角頂點(記為U)，將轉移至U。將最下方柵格中心點記為(X,Y)，分別判斷所在柵格的4個角頂點：D，D，D，D與終點的距離，選擇與終點距離最小的點作為轉移的目標角頂點(記為D)，將轉移至D。刪除與之間的中心柵格點，并將點U與點D相連。

判斷當路徑上存在水平線段時，將最左側柵格中心點記為，分別判斷所在柵格的4個角頂點：，L，L，L與起點的距離，將轉移到該柵格距起點最近的角頂點(記為L)上。將最右側柵格中心點記為，分別判斷所在柵格的4個角頂點：R，R，R，R與終點的距離，將轉移到該柵格距終點最近的角頂點(記為R)上。刪除與之間的中心柵格點，并將點L與點R相連。

步驟3.生成新路徑取代原有路徑。判斷路徑上是否仍存在水平線段或豎直線段，若仍存在則重新執行步驟2和步驟3，否則輸出機器人最終路徑。

路徑規劃的平滑改進能有效減小移動機器人的路徑長度及累計轉彎角度，使得機器人的能量消耗得以降低，更符合移動機器人的路徑規劃要求。路徑規劃平滑改進流程圖如圖4所示。

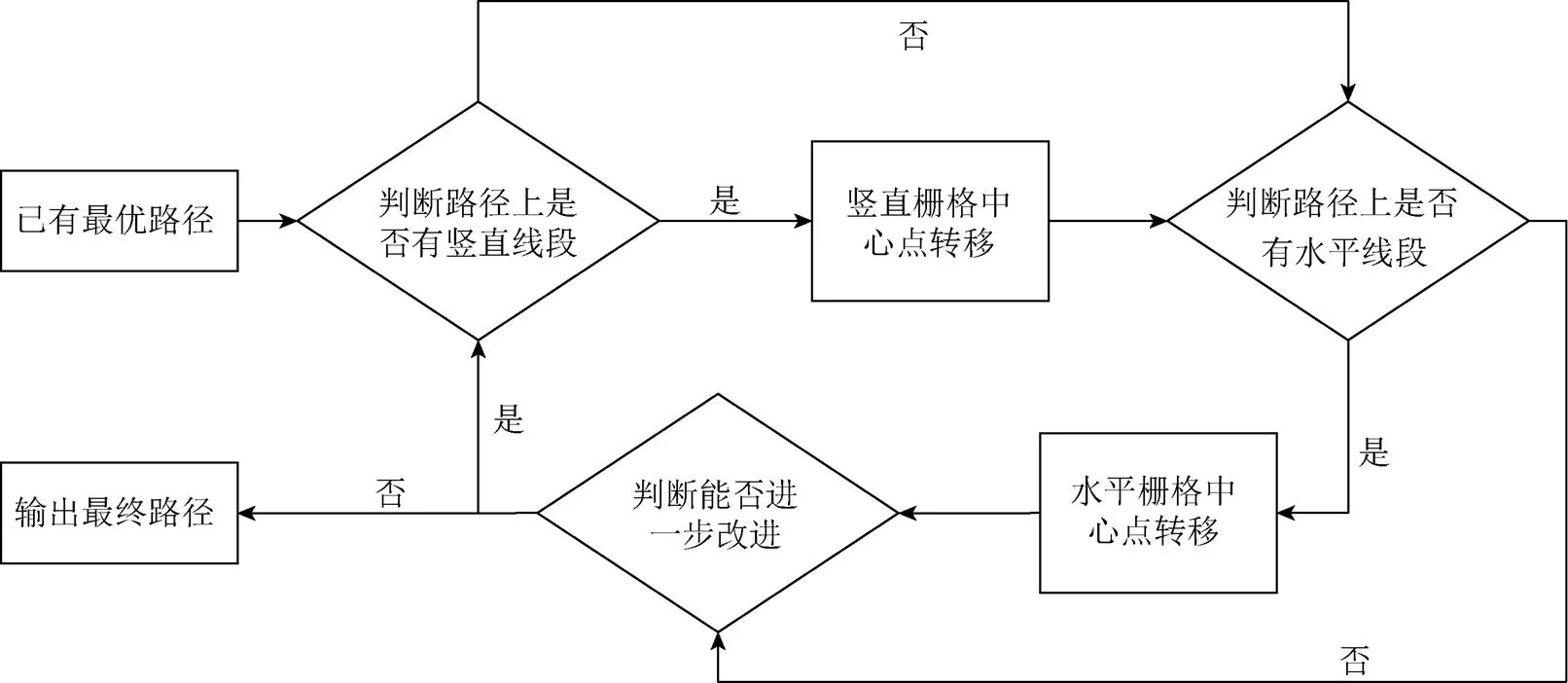
圖4 路徑規劃平滑改進流程圖

4 改進蟻群算法及路徑平滑操作的仿真驗證

4.1 仿真1

為驗證經過啟發因子改進的蟻群算法在移動機器人路徑規劃的正確性與有效性，對算法進行仿真。仿真環境為MATLAB R2016a，采用柵格法建模，柵格邊長為10。螞蟻個數=30，信息素重要程度參數=1，啟發因子重要程度參數=6，信息素蒸發系數=0.1，信息素增加強度系數=14。

在和均為默認值1的情況下，對基本蟻群算法及經過啟發因子更新方式、狀態轉移公式改進的蟻群算法進行仿真，路徑規劃仿真結果如圖5所示。

蟻群算法在搜索過程中進行下一節點選擇時存在著隨機性因素，僅根據一次實驗結果難以準確判斷兩種算法的優劣，因此需進行多次實驗來得到更準確的結果。為此，分別用MATLAB運行20次和50次，并對兩者的運行結果進行對比。

用MATLAB運行20次得到的路徑規劃統計結果見表1。

用MATLAB運行50次得到的路徑規劃統計結果見表2。

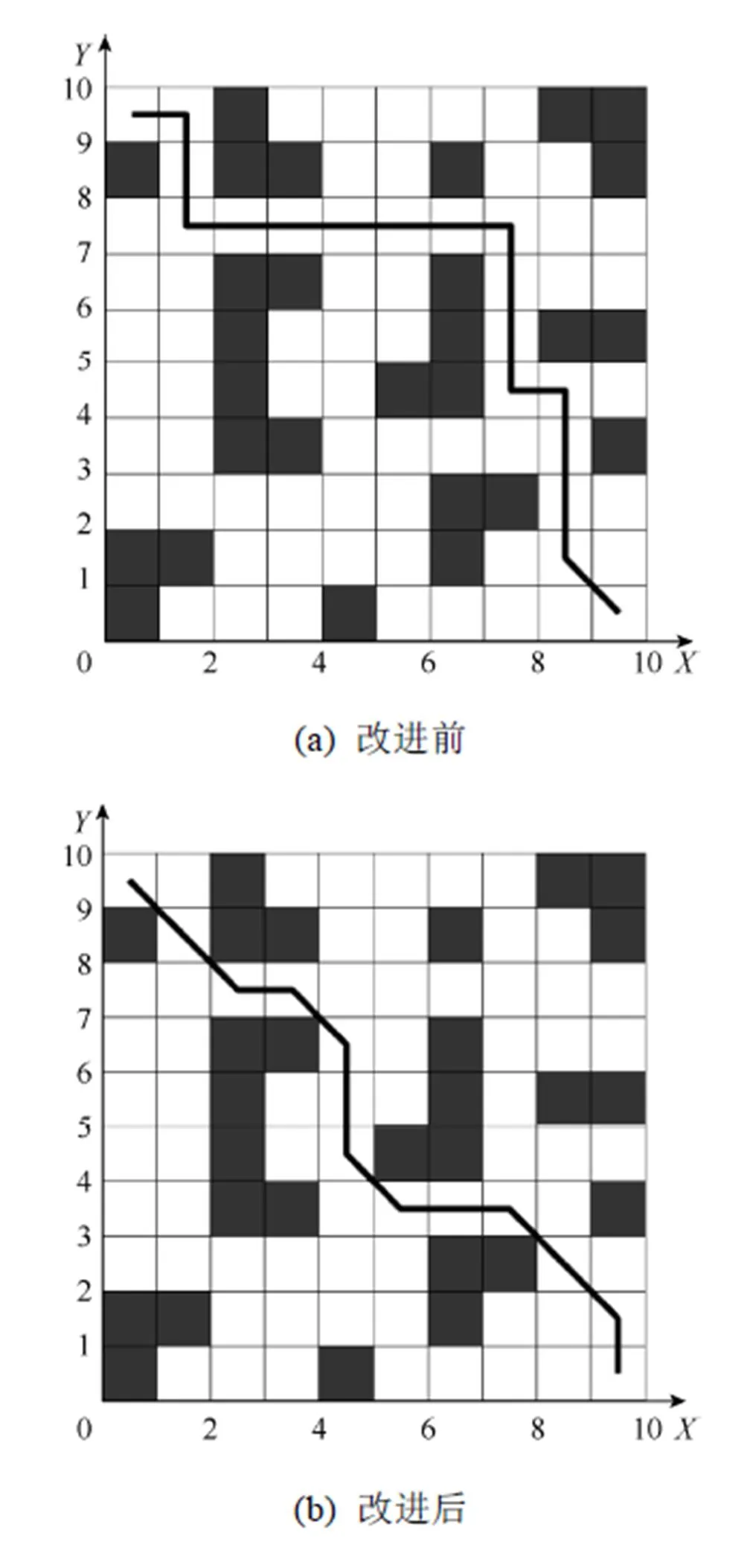
圖5 啟發因子更新方式、狀態轉移公式改進前后路徑規劃仿真結果

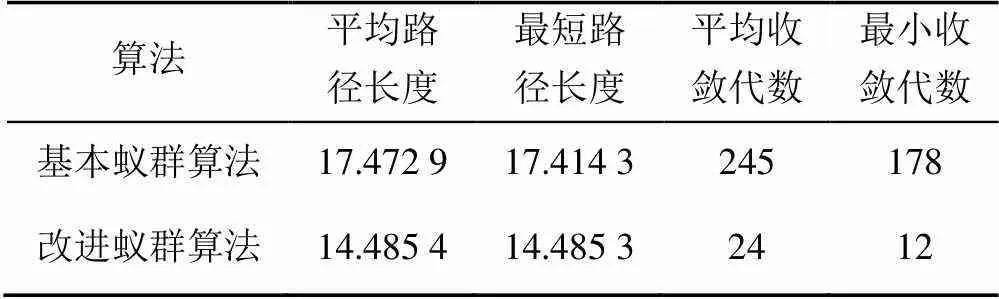
表1 a和b均為1時，運行20次的路徑規劃統計結果

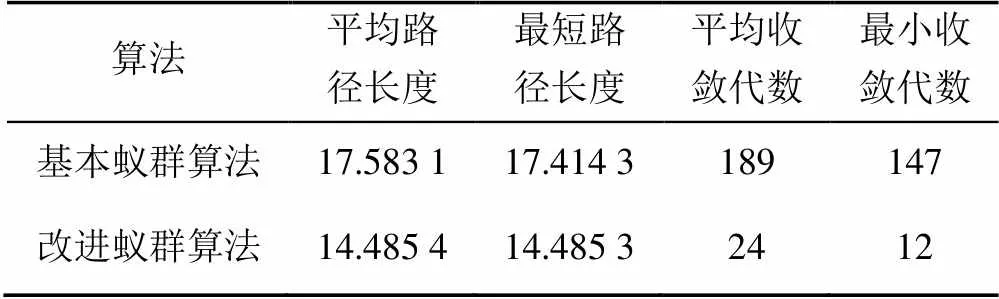
表2 a和b均為1時，運行50次的路徑規劃統計結果

由表1和表2比較分析可知，運行50次時，基本蟻群算法的平均路徑長度、平均收斂代數、最小收斂代數均發生變化。運行50次比20次包含更多的路徑搜索情況，以最小收斂代數為例，運行50次時為147，而運行20次時未出現此情況。因此，選擇用MATLAB進行50次獨立實驗，分析時采用MATLAB運行50次得到的路徑規劃統計數據。

由表2可知，啟發因子更新方式改進后的蟻群算法仿真出的平均路徑長度比基本蟻群算法減少了17.6%，最短路徑長度減少了16.8%。在平均收斂代數方面，改進蟻群算法比基本蟻群算法減少了87.3%。在最小收斂代數方面，改進蟻群算法比基本蟻群算法減少了91.8%。因此，在路徑長度及收斂速度上，經過啟發因子更新方式改進后的算法優于基本蟻群算法。

當和取不同值時，在10×10柵格環境下，對經過啟發因子更新方式改進的蟻群算法執行50次，路徑規劃統計結果見表3。

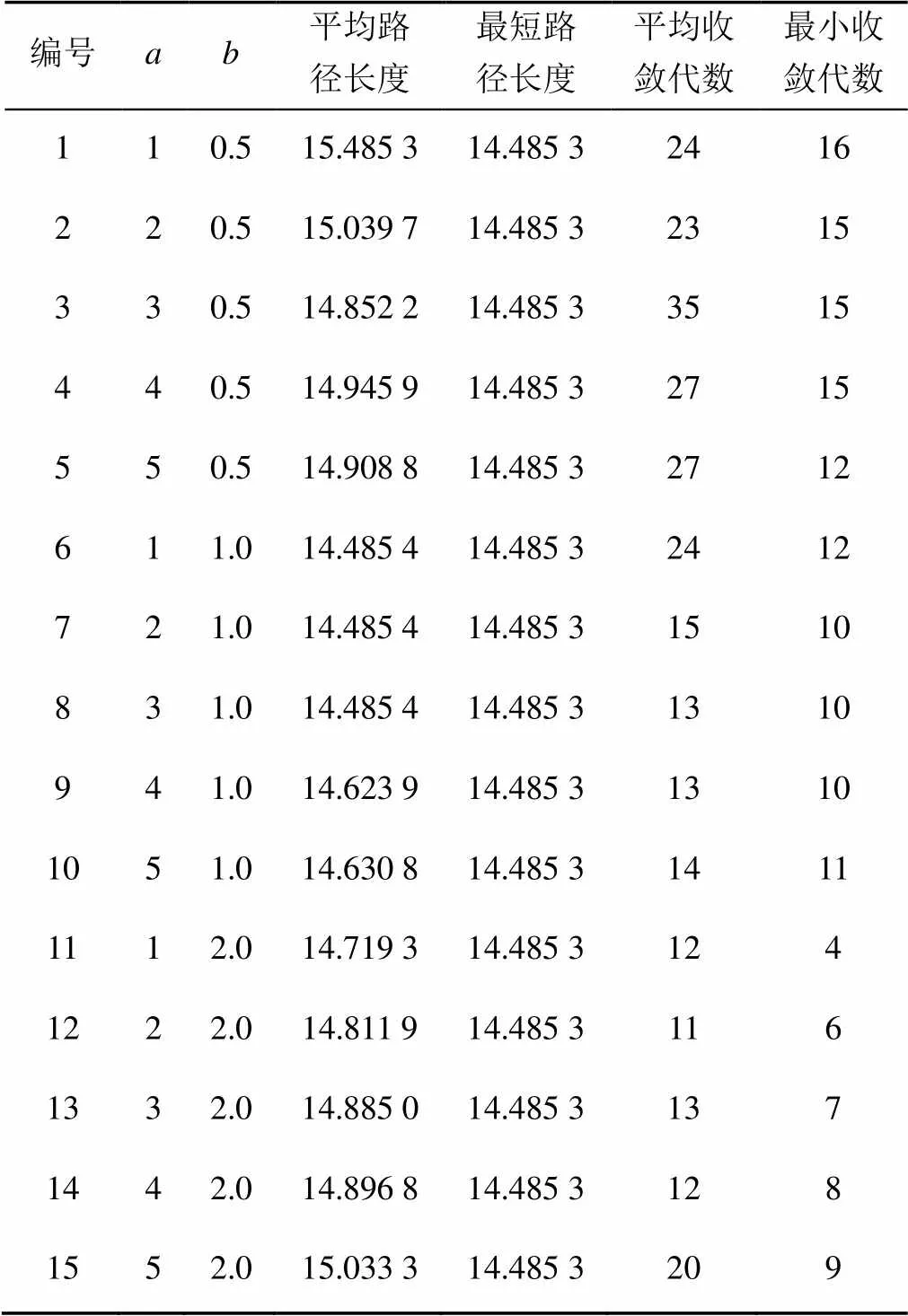
表3 當a和b取不同值時，改進蟻群算法路徑規劃統計結果

由表3分析可知，當=1；=1，2，3時，對經過啟發因子更新方式改進的蟻群算法執行50次得到的平均路徑長度均為最短，在保證具有最短路徑的前提下，當=3，=1時平均收斂代數及最小收斂代數最小，此時蟻群算法具有較好的收斂性能。與基本蟻群算法路徑統計結果相比，=3且=1時平均路徑長度減少了17.6%，平均收斂代數減少了93.1%。

4.2 仿真2

運用控制點轉移策略，對路徑規劃進行平滑改進，仿真結果如圖6和圖7所示。由圖6分析可知，在10×10柵格環境下，路徑規劃平滑改進后最優路徑長度為13.677 3，比原有路徑長度14.485 3減少了5.58%。改進前累計轉彎角度為315.000 0°，改進后累計轉彎角度為169.695 2°，減少了46.13%。

圖7在20×20柵格環境下，經過路徑規劃平滑改進后的路徑長度為27.329 0，比原有路徑長度28.041 6減少了2.54%。改進前轉彎角度為360.000 0°，改進后轉彎角度為147.479 3°，減少了59.03%。

采用控制點轉移策略后，平均路徑長度減少量為4.28%，平均轉彎角度減少量為52.58%。平滑改進前后數據對比見表4。

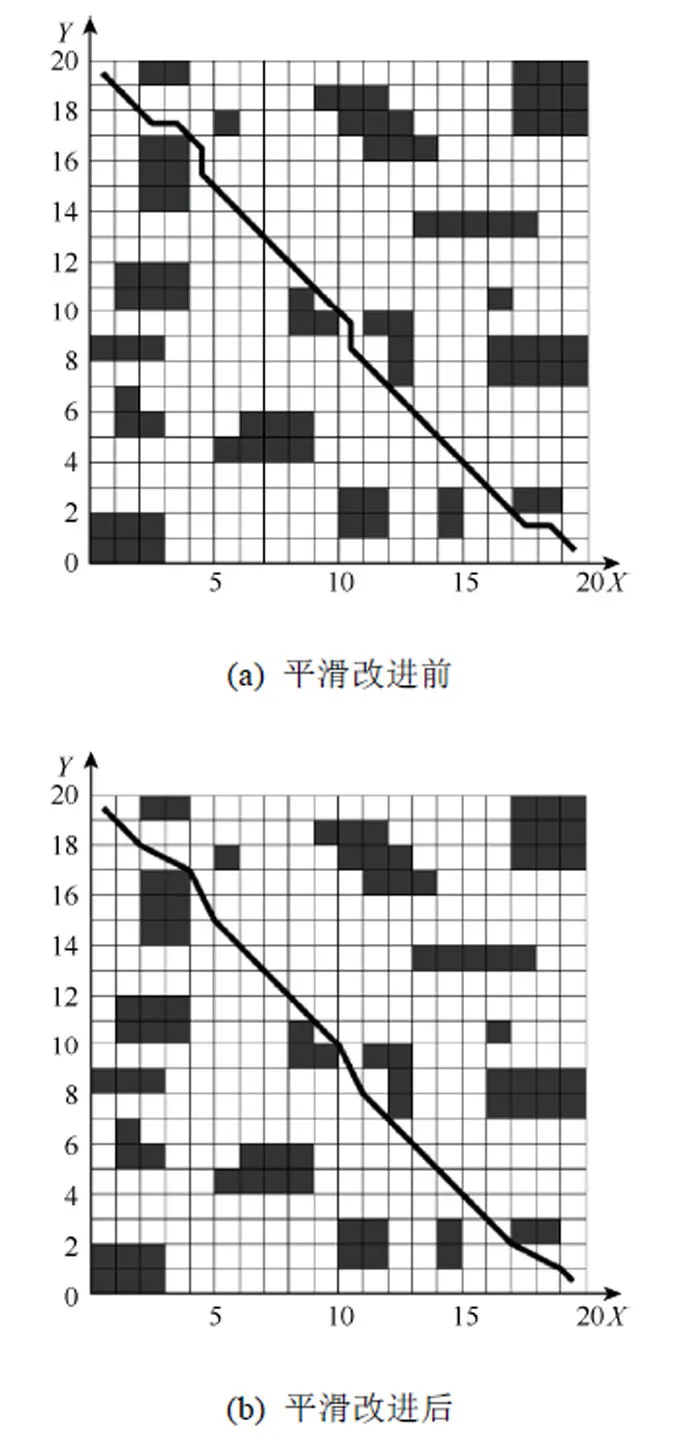
圖7 20×20柵格環境下平滑改進前后的路徑規劃

表4 路徑平滑前后對比

5 結束語

針對蟻群算法解決路徑規劃問題時存在的收斂速度慢的缺點，對啟發因子矩陣初始值及更新方式進行了改進，與基本蟻群算法相比，改進后平均路徑長度減少了17.6%，平均收斂代數減少了93.1%；對于在柵格環境下機器人累計轉彎角度大的問題，提出了控制點轉移策略，通過對控制路徑走向的柵格中心點向柵格角頂點的轉移，進一步縮短了路徑長度，實現了路徑規劃的平滑改進，平滑改進后機器人的平均路徑長度減少了4.28%，累計轉彎角度減少了52.58%。

[1] 栗紅生, 劉瑩. 復雜路徑下機器人路徑規劃優化方法仿真[J]. 計算機仿真, 2014, 31(1): 407-411.

[2] 趙開新, 孫新領, 王東署, 等. 基于改進蟻群算法的移動機器人路徑規劃研究[J]. 科技通報, 2017, 33(9): 76-79.

[3] GONG Y J, CHEN E, ZHANG X L, et al. AntMapper: An ant colony-based map matching approach for trajectory-based applications [J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(2): 390-401.

[4] 陳曉, 戴冉, 陳昌源. 基于Maklink圖和蟻群算法的航線規劃[J]. 中國航海, 2017, 40(3): 9-13.

[5] 張琦. 移動機器人的路徑規劃與定位技術研究[D]. 哈爾濱: 哈爾濱工業大學, 2014.

[6] DENG X Y, ZHANG L, LUO L. An improved ant colony optimization applied in robot path planning problem [J]. Journal of Computers, 2013, 8(3): 585-593.

[7] TANG B W, ZHU Z X, FANG Q, et al. Path planning and replanning for intelligent robot based on improved ant colony algorithm [J]. Applied Mechanics and Materials, 2013, 390: 495-499.

[8] 徐勝華, 宋樹祥, 佘果. 一種掃地機器人路徑規劃的改進算法[J]. 測控技術, 2017, 36(2): 120-123, 127.

[9] 張文強, 張彥. 基于改進蟻群算法的機器人三維空間路徑規劃[J]. 組合機床與自動化加工技術, 2018(4): 73-75.

[10] 朱艷, 游曉明, 劉升, 等. 基于改進蟻群算法的機器人路徑規劃問題研究[J/OL].計算機工程與應用. [2018-05-22]. http://kns.cnki.net/kcms/detail/11.2127.TP. 20180313.0951.014.html.

[11] 王輝, 王景良, 朱龍彪, 等. 基于改進蟻群算法的泊車系統路徑規劃[J]. 控制工程, 2018, 25(2): 253-258.

[12] 王志中. 基于改進蟻群算法的移動機器人路徑規劃研究[J]. 機械設計與制造, 2018(1): 242-244.

[13] 張瑋, 馬焱, 趙捍東, 等. 基于改進煙花-蟻群混合算法的智能移動體避障路徑規劃[J/OL]. 控制與決策. [2018-07-03]. https://doi.org/10.13195/j.kzyjc.2017.0870.

[14] 王紅君, 徐軍, 趙輝, 等. 基于平滑蟻群算法的機器人路徑規劃[J]. 燕山大學學報, 2017, 41(3): 278-282.

[15] 史恩秀, 陳敏敏, 李俊, 等. 基于蟻群算法的移動機器人全局路徑規劃方法研究[J]. 農業機械學報, 2014, 45(6): 53-57.

[16] 龔星宇, 常心坦, 賈澎濤, 等. 基于蟻群算法的井下救援路徑優化方法[J]. 工礦自動化, 2018, 44(3): 76-81.

[17] 顧軍華, 孟慧婕, 夏紅梅, 等. 基于改進蟻群算法的多機器人路徑規劃研究[J]. 河北工業大學學報, 2016, 45(5): 28-34.

[18] SHU J, WU L, HAN B, et al. Enhanced multi‐dimensional power network planning based on ant colony optimization [J]. International Transactions on Electrical Energy Systems, 2015, 25(7): 1204-1222.

[19] ZHANG W B, GONG X P, HAN G J, et al. An improved ant colony algorithm for path planning in one scenic area with many spots [J]. IEEE Access, 2017, 5: 13260-13269.

[20] 萬曉鳳, 胡偉, 方武義, 等. 基于改進蟻群算法的機器人路徑規劃研究[J]. 計算機工程與應用, 2014, 50(18): 63-66.

[21] 黃辰, 費繼友, 劉洋, 等. 基于動態反饋A*蟻群算法的平滑路徑規劃方法[J]. 農業機械學報, 2017, 48(4): 34-40.

Smooth Path Planning of Mobile Robot Based on Improved Ant Colony Algorithm

SUN Rui, ZHANG Wen-sheng

(School of Traffic and Transportation, Shijiazhuang Tiedao University, Shijiazhuang Hebei 050043, China)

A smooth path planning method based on improved ant colony algorithm is proposed for mobile robot in this paper.In order to overcome the disadvantage of slow convergence rate of ant colony algorithm in solving path planning problem,the initial value and updating method of the matrix of heuristic factors are improved. Compared with the results that the heuristic factor has not been improved, the average path length is reduced by 17.6%, and the average convergence algebra is decreased by 93.1%.The control point transfer strategy is proposed to solve the problem of large cumulative turning angle of the robot when obstacles exist in the grid environment.Based on the previous improvement,a smooth improvement of path planning is achieved by transferring the central point of grid to the vertex of grid. The path planning simulation results show that the average path length of the robot is decreased by 4.28% and the cumulative turning angle is reduced by 52.58%, compared with the non-smooth improvement.

ant colony algorithm; mobile robot; path planning; control point transfer strategy

TP 391

10.11996/JG.j.2095-302X.2019020344

A

2095-302X(2019)02-0344-07

2018-07-07；

2018-09-19

河北省重點研發計劃項目(18390324D)；石家莊市科學技術研究與發展計劃項目(181130034A，191260411A)；石家莊鐵道大學研究生創新項目(YC2019044)

孫 瑞(1995-)，女，河北衡水人，碩士研究生。主要研究方向為智能優化算法。E-mail：sunr3617@163.com

張文勝(1971-)，男，寧夏隆德人，教授，博士。主要研究方向為交通信息。E-mail：zws@stdu.edu.cn