基于橫向和縱向公平偏好的二層供應鏈網絡均衡決策

鄭英杰,周 巖

(青島大學管理科學與工程系,山東 青島 266071)

1 引言

隨著市場規模增長和競爭加劇，人們對供應鏈研究愈發重視。隨著供應鏈成員數量增加、分擔角色多樣化的變化，基于單一制造商和單一零售商的供應鏈模型，不能更好地反映現實中問題。由單一制造商和多個零售商形成的二層供應鏈網絡模型，能更好的描述此問題。

二層供應鏈網絡是一種常見的供應鏈結構，上層為一個決策者，占主導地位，下層是多個相互競爭的決策者，是追隨者，上下層之間是合作關系，下層是相互競爭關系，主導者和多個追隨者的決策影響其合作和競爭關系，其均衡決策在實際生產運營中尤為重要。典型的案例如蘋果公司等著名品牌與其下零售店形成的二層供應鏈網絡。但是由于下層零售商數量的增加，零售商不僅會關注與上層制造商之間的利潤分配，也會關注與同層其他零售商之間的利潤分配，形成零售商的縱向和橫向公平偏好行為。

已有較多學者針對二層供應鏈網絡進行研究。Lee等[1]基于一個制造商面對多個競爭零售商的二層供應鏈網絡研究了庫存策略。Roy等[2]在二層供應鏈網絡中研究了不確定市場下零售商的最優定價問題。國內，姚鋒敏等[3]建立了一個制造商和多個零售商的二層供應鏈網絡均衡模型，詳細描述了成員間的博弈關系和均衡決策問題。姚鋒敏和滕春賢[4]建立了二層供應鏈網絡競爭模型，研究表明上層可以通過一定的調控措施影響下層網絡的最優決策。周巖等[5]在二層供應鏈中分析了政府碳排放的調控機制對最優決策的影響。何麗紅等[6]在二層供應鏈中，研究了廣告努力水平和價格折扣對需求的影響。以上研究為解決此類問題提供了研究基礎和求解算法。

已有二層供應鏈網絡研究成果，都是基于決策者是完全理性且利己的假設。在傳統供應鏈中，一些學者引入決策者的公平偏好行為進行分析。Kahneman等[7]發現決策者不完全是自利的，會關注收益分配的公平性，提出公平偏好行為。基于Fehr和Schmidt[8]提出公平效用函數，近年來，分析供應鏈上下游成員間縱向公平偏好的成果較多。Cui等[9]將公平偏好首次引入供應鏈，分析了成員公平行為對渠道協調的影響。Katok和Pavlov[10]用實驗法研究了不公平厭惡和不完全信息等因素對供應鏈協調的影響。Qin Fai等[11]在信息不對稱下研究了公平偏好對供應鏈的決策影響。Patari等[12]提出用多準則決策方法研究公平效用。Liu Songsong和Papageorgiou[13]研究了通過轉移價格在多級供應鏈中實現利潤分配的公平性。國內，杜少甫等[14]在供應鏈中首次研究了零售商公平偏好行為對供應鏈契約的影響。杜少甫等[15]基于Nash討價還價模型建立公平效用參考框架，研究了供應鏈最優決策。李娟等[16]將公平細分后，研究了具有不同公平類型的零售商在批發價格契約下的訂購決策。劉云志和樊治平[17,18]考慮了供應商公平偏好且在不同市場下分析了VMI供應鏈協調問題。劉威志等[19]在不同定價策略下，分析了公平感知對二級供應鏈成員決策的影響。劉京等[20]研究了零售商具有公平偏好和風險規避的綠色供應鏈最優決策問題。

以上文獻都是基于單一制造商和零售商的傳統供應鏈分析上下游決策者間縱向公平偏好行為對供應鏈成員最優決策的影響。但是，一些學者將研究拓展到制造商與兩個競爭關系的零售商構成的供應鏈問題，分析了零售商之間的橫向公平偏好問題。Ho和Su Xuanming[21]在一個領導者和兩個追隨者問題中，研究了追隨者考慮橫向公平偏好對博弈結果的影響。Ho等[22]在一個制造商面對兩個零售商的供應鏈中，研究了考慮橫向、縱向公平偏好的供應鏈契約設計問題。Nie Tengfei和Du Shaofu等[23]在一個制造商和兩個零售商的供應鏈中，分析了其中一個零售商和制造商的縱向公平和與其他零售商橫向公平對數量折扣契約的影響。段丁鈺等[24]基于多個制造商和多個零售商的供應鏈網絡討論了零售商橫向公平偏好對均衡決策影響。

文獻[1-6]分析了二層供應鏈網絡最優決策。文獻[7-20]分析了傳統供應鏈中上下游決策者間縱向公平偏好行為對供應鏈成員最優決策的影響，但研究結果局限于傳統供應鏈上下游決策者間縱向公平偏好行為。文獻[21-23]分析了一個制造商面對兩個零售商的縱向公平和橫向公平偏好對供應鏈最優決策的影響。文獻[24]只研究了多個零售商間橫向公平偏好的供應鏈網絡均衡決策，沒有分析與制造商的縱向公平。基于以上分析和研究結果，本文基于下層多個零售商橫向、縱向公平偏好行為基礎上研究了一個制造商和多個(不少于兩個)相互競爭零售商構成的二層供應鏈網路問題。在完全信息下，下層零售商決策時，自身利潤少于同層其他零售商利潤，會帶來不滿與憤恨情緒，產生橫向公平偏好行為；自身利潤少于上層制造商利潤的參考值，也會帶來不滿與憤恨情緒，產生縱向公平偏好行為。構建考慮橫向和縱向公平偏好的多個競爭型零售商的Nash均衡模型、上層制造商和下層供應鏈網絡的Stackelberg-Nash博弈模型，利用罰函數法求解得到二層供應鏈網絡均衡決策。定性分析了橫向、縱向公平偏好權重、縱向公平參考系數對均衡決策的影響，并通過算例進行驗證。針對供應鏈各決策者如何應對公平偏好的負效用，提出合理化建議，使其在競爭市場中取得優勢。

2 問題描述

本文研究的二層供應鏈網絡結構如圖1所示，上層為一個制造商，下層由m(m≥2)個相互競爭的零售商和n(n≥2)個不同地域的需求市場構成，各層之間的商品交易用實線表示，箭頭表示商品流動的方向。

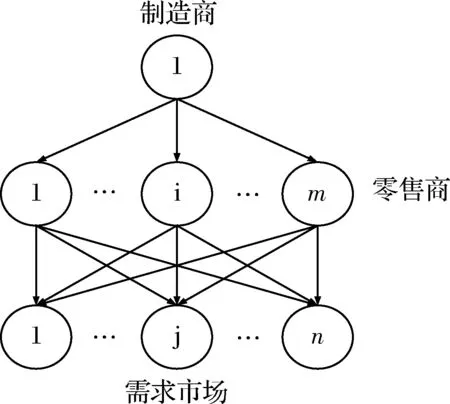
圖1 二層供應鏈網絡結構圖

上層制造商處于主導地位，下層多個零售商是追隨者，出售商品給需求市場的顧客。由于上層制造商不存在同層競爭者且相比下層利潤更大，所以假設是公平中性決策者，只考慮自身利潤最大化；下層為多個相互競爭的零售商和多個需求市場，零售商根據需求市場的需求量制定決策。在完全信息條件下，零售商i(i=1,…,m)決策時，首先考慮自身利潤最大化準則，當少于同層其他零售商利潤時，產生橫向公平最小化準則，當少于上層制造商利潤的參考值時，也會不滿與憤恨，產生縱向公平最小化準則。零售商在考慮利潤準則、橫向公平準則、縱向公平準則基礎上，得到效用函數做出最優決策。

由各成員博弈關系可知，上層制造商與下層多個零售商間具有Stackelberg博弈特征；下層多個零售商間具有Nash非合作博弈特征，在相互競爭中同時決策。所有零售商在銷售周期開始之前，根據市場需求，在考慮利潤、橫向和縱向公平偏好得到多準則效用函數，制定效用最大的訂購量和銷售量；制造商在獲得零售商訂購量后，制定實現利潤最大化的批發價格。需要的決策變量、費用函數、參數如表1、表2、表3所示。為了表示同層多個零售商間競爭關系[25]，費用函數Ci、Cij是同層決策向量的函數。為了保證均衡解的存在性，假設Ci為連續可微凸函數[25]。

表1 決策變量

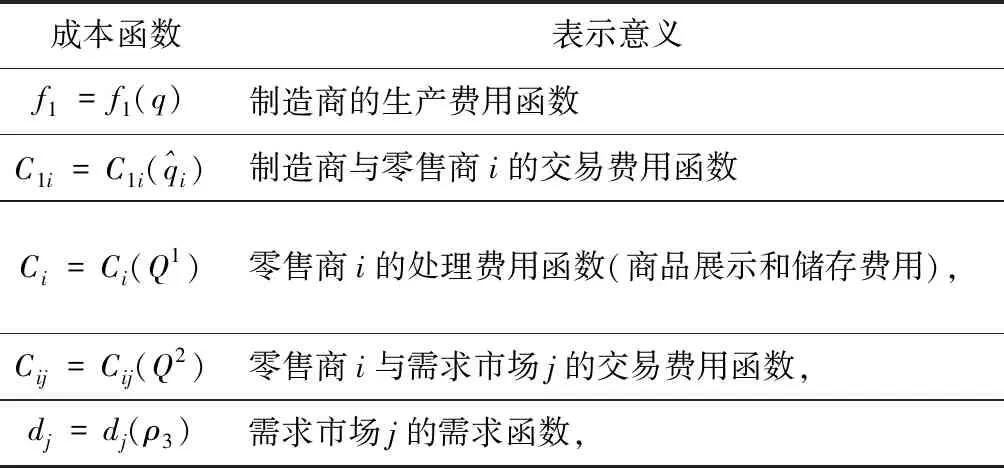
表2 費用函數

表3 相關符號與參數

假設供應鏈各成員在完全信息條件下決策。最優決策變量用*表示。

3 模型構建

這一節，先得到制造商利潤函數，再建立基于橫向、縱向公平偏好的多個競爭型零售商和需求市場的下層供應鏈網絡Nash均衡條件，最后得到上層制造商和下層供應鏈網絡的Stackelberg-Nash博弈模型。

3.1 制造商利潤

制造商利潤(記作πM)為：銷售商品給m個零售商的總收入減去生產、交易費用，則制造商的利潤表示為：

(1)

3.2 考慮橫向和縱向公平偏好零售商均衡條件

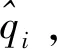
(2)

(3)

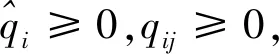
(4)

在完全信息條件下，零售商決策時，如果自身利潤少于同層其他零售商利潤，由于不滿與憤恨情緒產生橫向公平偏好行為。零售商i的橫向公平偏好行為，要求在下層多個零售商間，關于利潤分配的公平性，以自身利潤作為參考點，如果少于同層其他零售商利潤(同層其他零售商利潤,記作πt)，產生橫向公平偏好最小化問題：

(5)

如果零售商i利潤少于上層制造商利潤的參考值，也會由于不滿與憤恨情緒產生縱向公平偏好行為。零售商i以自身實際利潤作為參考點，如果自身利潤少于上層制造商利潤θ(θ∈[0,1])倍，產生縱向公平偏好最小化問題：

MinMax{θπM-πi,0}

(6)

利用基于公平的多準則決策方法[12]，得到零售商i考慮利潤準則(2)、橫向公平準則(5) 和縱向公平準則(6)的公平效用(記作Ui)最優化問題：

(7)

假設零售商的利潤均不相同，從大到小排序如下：π1>···>πh>···>πi>···>πm。記零售商i的利潤低于零售商h(h∈[1,i-1])，則零售商h的數量有i-1個。假設θπM>πi，即縱向公平存在。則公平效用(7)可表示為：

(8)

證明：由式(8)和約束(3)，得到公平效用最大化問題(7)的拉格朗日函數(記作Li)為：

(9)

其中λi為約束(3)的拉格朗日乘子變量。

由式(1)和(2)得：

(10)

(11)

(12)

(13)

(14)

(15)

(16)

同理，由式(12-13)，分別得：

(17)

(18)

聯立方程(16)-(18)，得：

(19)

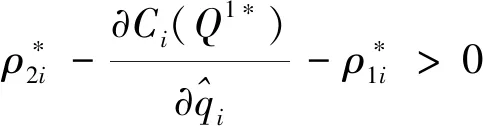
推論1進一步說明，當零售商i由于利潤同層分配不均產生橫向公平偏好，且公平偏好權重不斷增大時，為了擺脫在同層競爭中的不利地位，試圖通過增加其訂購量的方式，在市場競爭中取得優勢，使下層零售商間利潤分配趨于公平。

證 明：由推論1的證明方法得：

(20)

推論2得證。

推論2進一步說明，當零售商i由于在上下層利潤分配不均產生縱向公平偏好，隨著縱向公平偏好權重增大，零售商i會增加其商品訂購量，增加自身的利潤，使上下層利潤分配趨向公平。

證 明：由推論1的證明方法得：

(21)

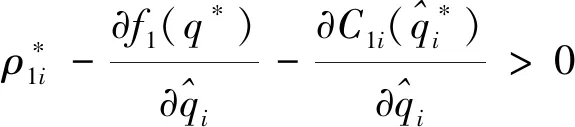
推論3進一步說明，當零售商i縱向公平參考系數不斷增大，可視為與縱向不公平的標準提高，零售商i通過增加其訂購量的策略，縮小與制造商利潤參考標準的差距，保證在上下層利潤分配的公平性。

(22)

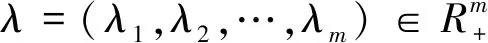
證 明：由式(11)-(13)一階最優性條件得到。

3.3 需求市場的均衡條件

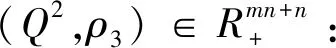
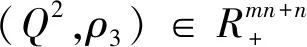
(23)

(24)

3.4 考慮零售商橫向和縱向公平偏好的下層供應鏈網絡均衡條件

(25)

3.5 考慮零售商橫向和縱向公平偏好的二層供應鏈網絡最優決策

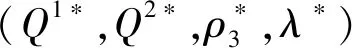
(26)

4 求解算法

在第3節，考慮零售商橫向和縱向公平偏好的二層供應鏈網絡最優決策問題，表示為一個具有變分不等式約束的二層規劃問題[27]，由于約束的復雜性，式(26)直接求解很困難。利用變分不等式和非線性互補問題的等價性[26]，把下層約束轉化為等式和不等式約束，則問題(26)，轉化為單層非線性規劃問題。通過罰函數法[28]，可求解得到考慮零售商橫向和縱向公平偏好的二層供應鏈網絡均衡決策。式(26)中，下層變分不等式約束用如下非線性互補問題表示[26]：

(27)

把式(27)中等式約束構造為式(26)中目標函數罰函數項，則具有變分不等式約束的二層規劃問題(26)可轉化為如下帶有罰函數的單層非線性規劃問題：

(28)

其中M>0為懲罰因子。只有式(28)中罰函數項等于0，問題(26)目標函數才能實現最大。即當M>0時，問題(28)的最優解就是問題(26)的最優解[28]，得到考慮零售商橫向和縱向公平偏好的二層供應鏈網絡均衡決策。

算法步驟：

步驟1 給定初始懲罰因子M和步長；

5 數值算例

本節通過數值算例驗證第3節模型、性質的有效性，分析零售商橫向、縱向公平偏好對均衡決策、利潤和效用的影響。算例中上層由1個制造商、下層由4個零售商和3個需求市場構成。費用函數(根據文獻[24]算例1修改得到)：

制造商生產費用：f(q)=0.25q2+0.2q。

制造商與零售商i交易費用：

需求市場j的需求函數：

d1(ρ3)=-2ρ31-1.5ρ32+1000

d2(ρ3)=-2ρ32-1.5ρ33+1000

d3(ρ3)=-2ρ33-1.5ρ31+1000

零售商i的處理費用：

零售商i與需求市場j交易費用：

Cij(Q2)=0.5qij+5,i=1,2,3,4,j=1,2,3

算例中調整零售商i的處理費用Ci(Q1)，使得4個零售商的利潤滿足π1>π2>π3>π4。

算例1 分析零售商橫向公平偏好對均衡決策、利潤和效用的影響

在算例1中固定縱向公平偏好權重和參考系數，分析零售商橫向公平偏好對均衡決策、制造商利潤和零售商效用影響。

固定縱向公平參考系數θ=0.2，且固定零售商縱向公平偏好權重γi為0(即不考慮縱向公平、只考慮橫向公平)、0.1(即同時考慮橫向和縱向公平)，令橫向公平偏好權重αi取值0、0.1、0.2，通過Matlab編寫第4節算法程序，求解得出均衡決策結果如表4所示；制造商利潤、零售商效用結果如表5所示。

由表4可看出：

(1)當零售商只考慮橫向公平，由表4的3-4列，零售商訂購量和銷售量相比公平中性結果(第2列)增加，且隨著橫向公平偏好權重進一步增大，與推論1結論相符；制造商給出處于劣勢地位零售商2、3、4的批發價格減小。

(2)當零售商同時考慮橫向、縱向公平，由表4的5-7列，決策變量隨橫向公平偏好權重的變化趨勢相同，但相比只考慮橫向公平結果，考慮橫向、縱向公平的零售商2、3、4以更低的批發價格從制造商處訂購更多的商品。

由表5可看出：相比公平中性結果，零售商考慮橫向公平時，制造商利潤增大，零售商2、3、4利潤增加但效用減小，且隨著公平偏好權重進一步變化。零售商在利潤增加的情況下效用減少，因為隨著自身橫向公平偏好權重的增加，零售商對于利潤分配公平的要求越高，雖然其利潤增大，但由橫向公平產生的負效用進一步增大，導致其效用下降。說明零售商的橫向公平偏好行為，對制造商有利，但不利于零售商的效用提高。

算例1結果說明：零售商的橫向公平偏好行為，會使其訂購量和銷售量增加，且制造商的批發價格減小。隨著橫向公平偏好權重的增大，在不利地位的零售商對公平感知提高，在市場中試圖通過增大商品交易量的策略，獲取更高利潤，擺脫劣勢地位。

在實際的生產運營中，對于考慮橫向公平偏好的零售商，分析橫向公平產生的根本原因，通過優化生產運作管理，向高利潤者看齊。如降低成本、加大產品宣傳力度等問題，提高自身市場競爭力，縮小與市場領跑者之間的差距，才能真正實現橫向公平。

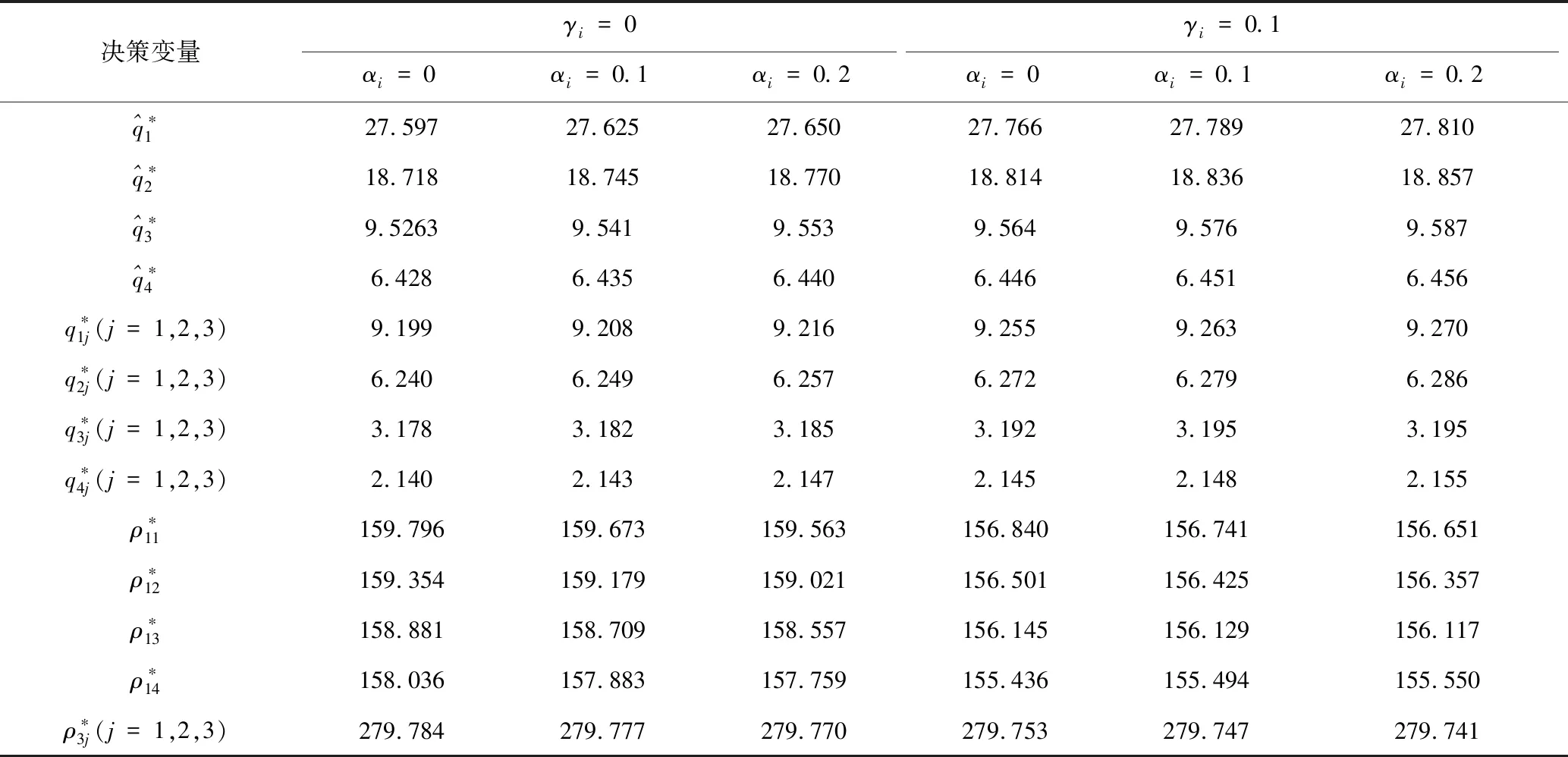
表4 算例1均衡決策結果

表5 算例1決策者的利潤/效用

算例2分析零售商縱向公平偏好對均衡決策、利潤和效用的影響

在算例2中固定橫向公平偏好權重和縱向公平參考系數，分析零售商縱向公平偏好對均衡決策、制造商利潤和零售商效用的影響。

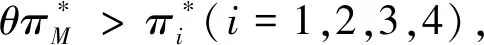
令縱向公平偏好權重γi取值0、0.1、0.2，通過Matlab編寫第4節算法程序求解得出均衡決策結果如表6所示；制造商利潤、零售商效用結果如表7所示。

由表6可看出：

(1)當零售商只考慮縱向公平偏好，由表6的3-4列，零售商訂購量和銷售量相比公平中性結果(第2列)增加，且隨著縱向公平偏好權重增大，與推論2結論相符；同時上層制造商給處于縱向劣勢地位零售商的批發價格減小。

表6 算例2均衡決策結果

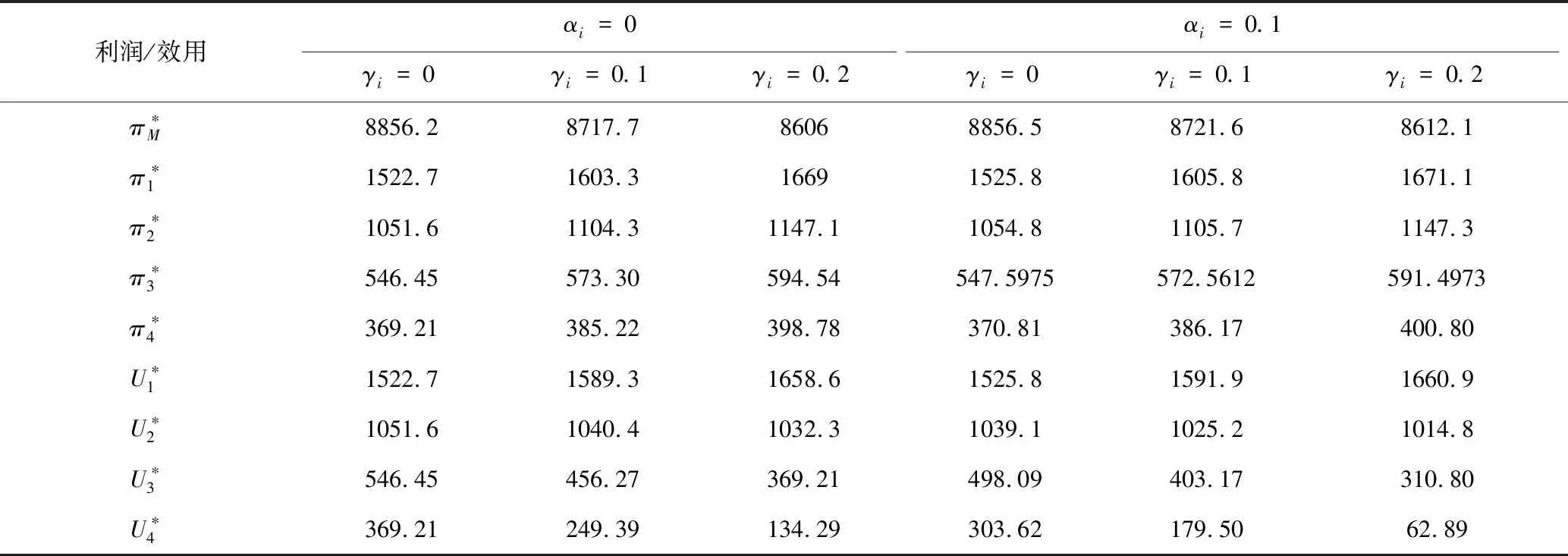
表7 算例2決策者的利潤/效用

(2)當零售商同時考慮橫向、縱向公平，由表6中5-7列可以看出，決策變量隨縱向公平偏好權重的變化趨勢相同，但相比只考慮縱向公平結果，考慮橫向和縱向公平的零售商以更低的批發價格從制造商處購買更多的產品。

由表7可看出：相比公平中性結果，零售商考慮縱向公平，制造商獲得利潤減小，零售商獲得的利潤增加、效用增加。隨著縱向公平偏好權重進一步變化，零售商縱向公平偏好使利潤從上層制造商向下層零售商流動，上下層利潤分配趨于公平。

算例2結果說明：零售商的縱向公平偏好行為，導致自身訂購量和銷售量增加，制造商批發價格減小且調節幅度相比算例1更明顯。隨著縱向公平偏好權重增大，零售商在上下層分配不公平感知提高，零售商試圖通過增大商品的交易量、獲得較低批發價格，壓低制造商利潤，同時增加自身利潤，縮小與制造商利潤參考值間的差距。

在實際的生產運營中，考慮了縱向公平偏好的零售商，提高了自身利潤和效用，但對于縱向公平權重的增大，會導致制造商利益受損，不利于供應鏈穩定。因此，制造商和零售商應在利潤分配方面積極協商，在保證供應鏈穩定的基礎上將零售商對縱向公平的重視程度控制在雙方可以接受的范圍。

算例3分析零售商縱向公平偏好參考系數對各成員均衡、利潤和效用的影響

當零售商考慮橫向、縱向公平偏好，公平權重相同且固定時，分析縱向公平參考系數對均衡決策、制造商利潤和零售商效用的影響。

固定零售商橫向、縱向公平偏好權重αi=γi=0.1，以步長0.05調整零售商縱向公平參考系數θ從0.2變化到0.4，通過Matlab編寫第4節算法程序求解得出均衡決策結果如表8所示；制造商利潤、零售商效用隨θ的變化趨勢如圖2、圖3所示。由表8可以看出：

(1)當零售商考慮橫向、縱向公平偏好時，隨著縱向公平參考系數θ增大，零售商與制造商之間的訂購量增加，與推論3結論相符。制造商給處于劣勢地位零售商的批發價格減小。因為隨著縱向公平參考系數θ增大，零售商縱向公平的參考標準提高，零售商在獲得同樣利潤時，與參考值的差值增大，產生更強的縱向公平行為。因此零售商在市場中試圖增加更多的商品交易量的策略，擺脫不利地位。

(2)由圖2、3可知，隨著縱向公平參考系數θ增大，制造商獲得利潤減小，零售商的利潤增加、效用減小。說明零售商縱向公平參考系數的增加不利于制造商利潤、零售商效用的提高；雖然零售商利潤上升、制造商利潤下降，但縱向公平參考系數增大，由于縱向公平偏好產生的負效用仍然是增大的，所以獲得的效用減小。

算例3結果說明：零售商縱向公平參考系數θ增加直接影響零售商縱向公平偏好產生的效用大小，不利于制造商利潤、零售商自身效用的提高。在實際生產運營中，制造商應多與零售商溝通，給予劣勢零售商優惠的批發價格，爭取共同協作提高供應鏈整體效益；同時零售商應制定合適的縱向公平參考標準，實現自身效用提升。

表8 算例3均衡決策結果

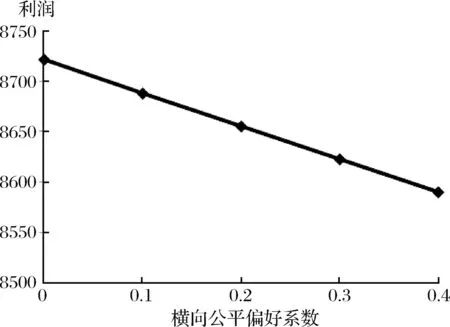
圖2 制造商利潤隨θ的變化趨勢

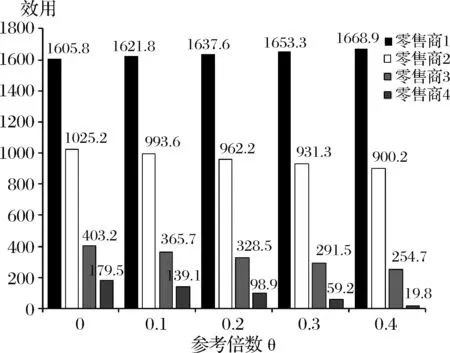
圖3 零售商的效用隨θ的變化趨勢

6 結語

本文針對上層為單一制造商下層為多個競爭性零售商和需求市場的二層供應鏈網絡問題,研究了零售商的橫向和縱向公平偏好行為。研究結果說明：

(1)零售商的橫向公平偏好行為，會降低上層制造商批發價格，增大下層零售商的訂購量銷售量；制造商利潤增大，零售商利潤增加但效用減小。建議零售商為了在同層零售間取得優勢地位，應通過優化生產運營，降低運營成本，提高效率實現橫向公平。

(2)零售商縱向公平偏好行為，會降低制造商批發價格，增加下層零售商的訂購量；制造商利潤減小，零售商利潤增加且效用增加。建議制造商應多與零售商溝通，相互交流學習，共同開發市場，提高供應鏈整體效益，通過實現零售商利潤提高減少縱向公平負效用。

(3) 零售商的縱向公平參考系數，也會使上層制造商批發價格減少，下層零售商的訂購量增加；制造商利潤減小、零售商利潤增加、效用減小。說明零售商縱向公平的標準提高，對供應鏈各成員均造成損失，不利于供應鏈整體和各成員目標的實現。建議零售商降低上下層利潤分配標準，與上層制造商溝通發展。對于制造商應多與零售商溝通，各方協作互助，實現效用最大和公平雙贏的局面。

制造商作為二層供應鏈網絡的主導者，在生產活動中為了提高其自身的利潤，應從零售商的多種行為和心理認知角度出發，增進上下層溝通，鼓勵零售商同層間相互學習與合作，共同開發市場，實現零售商間利潤分配公平才能保障客戶的穩定性，保證自身利潤。

本文在完全信息下，在二層供應鏈網絡中討論了零售商公平偏好行為；未來可以繼續討論信息不對稱情形下零售商的公平偏好行為對供應鏈最優決策的影響。