基于限制合作博弈的產業集群企業利益分配研究
王大澳,菅利榮,王 慧,劉思峰
(1.南京航空航天大學經濟與管理學院,江蘇 南京 211106;2.北京交通大學經濟與管理學院,北京 100044)
1 引言
產業集群作為當前產業發展中的一種重要形式,具有技術創新密集、規模經濟突出和知識溢出等特征。產業集群形成后,集群內部的企業組成協同創新聯盟,通過聯盟合作促進集群內新興創新企業的快速繁衍、成長,使相關產業得到延伸,逐漸形成協同創新網絡,構成完整的產業鏈條,提升科技與知識創新的效率,形成持續創新發展的機制,進而有力帶動整個新興產業的發展。然而影響聯盟企業合作最為關鍵的因素是如何合理公平的對組成聯盟所獲取的利益進行分配,利益分配是否合理直接影響聯盟創新的可持續性和穩定性。
如何有效解決合作聯盟內的收益分配問題已成為國內外研究的重要課題。Shapley值及其改進的方法是研究合作聯盟企業利益分配問題的重要方法之一。Shapley值是由Shapley于1953年提出的一種用以解決n人合作中利益分配問題的數學方法[1]。傳統的Shapley值方法以合作聯盟中每位成員具有相同的邊際貢獻為前提假設,然而在實際情況中,政治、經濟、環境等因素可能會對聯盟成員形成一定的約束。Aumann和Maschler最早提出了具有限制的合作博弈模型[2]。隨后學者們探討了參與成員之間其他形式的合作限制。Myerson通過無向圖來描述成員之間是否具有雙邊交流,將連通圖作為對可行聯盟的限制,只有成員之間具有連接關系,他們才可以形成合作[3]。Gilles假設一個成員必須獲得至少一個他的上級成員的許可才能和其他成員進行合作[4];Derks假設上級和下級所具有的權重不同,任何上級可以否決其下屬的行為,因此成員必須得到所有上級的許可才可參與合作[5-6]; Béal 等[7]在研究具有限制性可能的合作博弈中,擴展了Herings等[8]提出的樹形結構的平均邊際樹解,并獲得了這些解的一些新的特性;孫紅霞和張強[9]基于Faigle和Kern[10]提出的格結構思想,研究了具有聯盟結構的限制合作博弈。張瑜等[11]利用網絡協同系數對Shapley值進行優化對產業技術創新戰略聯盟中的創新主體在合作過程中的利益協調問題進行了研究。上述文獻中考慮具有限制的合作博弈問題,前提條件都是參與人之間的依賴關系必須是完整的,即在一個聯盟中一個成員要么被允許完全合作,否則他們不能參與合作。
然而在實際的聯盟合作中,企業在參與合作時,由于自生技術的局限性,產業集群環境的不確定性,企業只能發揮出一部分能力。企業之間以一定的參與率參加到聯盟合作中,他們之間的收益分配問題具有非可加性。為了解釋和刻畫這種問題,就要弱化概率公理化刻畫中可加性的條件。法國數學家Choquet[12]在1954年提出了關于容度的理論,來解釋非可加的測度,并提出了有界隨機變量關于容度的Choquet積分。Choquet積分是一種不滿足可加性測度的非線性積分,是解決屬性之間具有關聯性的問題有效方法。如趙樹平等[13]運用Choquet積分解決屬性之間具有關聯性的決策問題。現有的文獻中已有很多學者利用Choquet理論對聯盟成員以某種程度參與到聯盟合作中的情況進行了研究。Gallardo等[14]考慮到聯盟中的成員可能具有一定的自由度參與合作的情況,構建了聯盟中參與人可主觀的確定限制的博弈模型。孫紅霞和張強[15]將經典合作博弈中的勢函數和一致性推廣到具有模糊聯盟的合作博弈中,研究了具有模糊聯盟博弈的Shapley值。孫紅霞[16]研究了模糊聯盟結構的合作對策的分配問題,定義了Chouqet積分形式的模糊聯盟核心,并證明了Chouqet積分形式模糊Owen值屬于其所對應的模糊聯盟核心。孟凡永和張強[17]研究了具有Choquet積分形式的模糊合作對策,并對其單調性和連續性進行了研究。單而芳和張廣[18]結合權重的思想對準許樹結構(即局中人的活動需要經得其他局中人的準許才能生效)的博弈進行了研究,并對準許樹博弈限制核的研究,證明了當準許樹博弈滿足錐模性質時由權重系統集確定的解集與它的準許樹限制核是等價的。楊靛青等[19]針對模糊環境下有限制的聯盟合作情況,利用Choquet積分定義了模糊聯盟圖合作對策τ值,證明了其存在性和其他重要性質。
上述文獻中考慮了具有聯盟結構的合作博弈問題,但在實際的產業集群聯盟合作中,由于集群環境的復雜性、不確定性和企業自我認識的局限性,有時很難完全確定信息的精確值。然而鄧聚龍[20]提出的灰色系統理論對這類 “部分信息已知,部分信息未知”的小樣本,貧信息的問題可以進行很好的刻畫。鑒于此,在前人研究的基礎上,本文將灰數、Choquet積分和Shapley值模型相結合,提出了基于灰色授權機制的限制合作博弈,進而解決產業集群中企業的合作能力和聯盟收益值均為區間灰數,且企業之間具有關聯性的聯盟利益分配問題。
2 理論基礎
2.1 合作博弈
設有限局中人集合N={1,2,3,…,n}上具有效用可轉移的合作對策,是一個二元組,(N,v),其中v:2N→是定義在所有子集上的特征函數,且滿足v(?)=0;對任意S1,S2∈2N滿足S1∩S2=?,v(S1∪S2)≥v(S1)+v(S2)。一般情況下,通過特征函數v來識別一個合作博弈(N,v),給定一個聯盟E?N,v(E)為聯盟E的值,表示在聯盟E中局中人共同協作獲得的收益。如果博弈v是單調的,對于任意F?E?N,則有v(F)≤v(E)。將N上所有經典合作對策記為G(N)。
定義1 在n人合作博弈(N,v)中,G(N)的Shapley值是n維向量:φ(v)=(φ1(v),φ2(v),…,φn(v)),φi(v)的值為i在G(N)中獲得的收益:
×[v(E)-v(E{i})]
(1)
其中|E|表示聯盟E中局中人的數量,且Shapley值滿足以下三條公理:
可加性公理:對任意ω,v∈G(N)及任意的S∈2Ni∈N,有(ω+v)(S)=ω(S)+v(S),則φi(ω+v)=φi(ω)+φi(v), ?i∈N。
對稱性公理:如果對于N集合中所有不包含i和j的子集E,有v(E∪{i})=v(E∪{j}),則φi(v)=φj(v)。
啞元性公理:令v∈G(N),對任意的i∈N,如果v(E)=v(E{i}),E?N,則i為啞元,即φi(v)=v({i})。
2.2 區間灰數
定義2 設?1∈[a,b],a

定義4[22]設區間灰數?1,?2為兩個標準灰數,S(?1),S(?2)為對應的相對核,P(?1),P(?2)為對應的精確度。
(1)若S(?1) (2)若S(?1)>S(?2),則標準灰數?1??2; (3)若S(?1)=S(?2),則 ①若P(?1)=P(?2),則標準灰數?1=?2; ②若P(?1) ③若P(?1)>P(?2),則標準灰數?1??2。 定義5 設X={x1,x2,…,xn}為非空集合,P(X)是X的冪集,f:(X,P(X))為定義在X上的非負函數,μ為定義在P(X)上的容量,則f關于容量μ的Choquet積分為: (2) 其中,0≤f(x(1))≤f(x(2))≤…≤f(x(n)),A(i)={x1,x2,…,xi}且A(0)=0。 Choquet積分具有以下性質: 在實際的產業集群聯盟合作中,企業由于自生技術的局限性只能發揮出一部分能力,當和其他企業形成聯盟時在其他企業技術的支持下獲得更多的生產能力,即為其他企業對該企業進行的授權。灰色授權機制是指企業在聯盟中的合作能力為不確定的灰色信息。 定義6 設τ:2N→[0,1]N為N上的灰色授權算子,記為gso(N),且滿足: (1)τ(E)≤1E,E?N (2)如果E?F?N,則 τ(E)≤τ(F)。 假設τ是一個灰色授權算子,v是N上的博弈。給定一個聯盟E?N和i∈N,則τi(E)為企業i在聯盟E中的合作程度。 定義7 設v∈G(N)和τ∈gso(N)。v在τ上的限制博弈vτ∈G(N)的Choquet積分定義為: (3) (4) 其中0=?(0) 定義8 在n個企業的灰色授權機制的合作博弈為φ:G(N)×gso(N)→,則有φ(v,τ)=φ(vτ);v∈G(N),τ∈gso(N)。 定義9 在n個企業的灰色授權機制的合作博弈τ∈gso(N)中,設D?N是一個聯盟。如果對任意聯盟E?N,都有 (5) 則稱聯盟D為一個支柱。 定義10 在n個企業的灰色授權機制的合作博弈τ∈gso(N)中,的Shapley值是n維向量φ(v)=(φ1(v),φ2(v),…,φn(v))。 滿足以下四條公理: (2)對稱性公理:對于置換π,有φπi(πvτ)=φi(vτ)。 (3)可加性公理:對于任意v,ω∈G(N),τ∈gso(N)對任意的i∈N,有φi(v,τ)+φi(ω,τ)=φi(v+ω,τ)。 (4)啞元性公理:對于任意v∈G(N),τ∈gso(N),D為支柱,D?N,對任意的i∈ND,有φi(v,τ)=vτ({i})。 引理1 設合作博弈G=(N,uT)是一個簡單的博弈,其中合作聯盟T?N實值函數uT的取值為:如果T?N,則uT(N)=1;否則,uT(N)=0。 具體證明參考文獻[23]。 定理1具有灰色授權機制的限制合作博弈,若滿足有效性、對稱性、可加性和啞元性,則存在唯一的Shapley 值: ×[vτ(E)-vτ(E{i})] (6) 證明:對定理1的證明分為兩部分,第一部分先證明由公理可以推導出唯一的式(6)表示的Shapley值。第二部分證明公式(6)滿足四條公理。 由引理2可得: 由公理3和引理1的推論式,有 將引理2中的cT代入上式,并將聯盟R換成聯盟E,有 (7) 對式(7)分開討論,前一部分有: (8) 后一項中,因為i?E令E′=E∪{i}則E=E′{i},|E|=|E′|-1,于是,后一項為 (9) 將式(9)代入到式(7),再將式(8)代入,有 (10) 在i?E的時候式(10)中vτ(E)-vτ(E{i})=0,則式(10)和式(6)沒有區別,這樣我們完成了由公理可以推導出唯一的式(6)表示的Shapley值。 證明的第二部分驗證唯一的Shapley 值滿足合作博弈的四個公理。 驗證對稱性:對任意一個置換π,都是對N中n個元素的一種排序。令π2=π*π也是一種置換,π和π2的逆變換也是如此。因此對任意的E?N,有|π(E)|=|π-1(E)|=|E|。 令ε=(π*π)-1=(π2)-1 ×[πvτ(πE)-πvτ(πE{i})] ×[vτ(E)-vτ(E{i})]=φi(v) 驗證有效性:設v∈G(N),τ∈gso(N)E?N,D為一個支柱,運用Shapley值的有效性和Choquet積分的公理1。 對式(6)關于i求和得到: (11) 考慮一個固定的聯盟L?N,則式(11)括號中的第一項變為vτ(L),且總共出現|L|次,則整個和式中vτ(L)的系數為: (12) 上式對于一切聯盟L?N都成立。 式(11)括號中的第二項變為vτ(L{i}),且總共出現n-|L|次,則整個和式中vτ(L{i})的系數為: 其中(|L|+1)是指聯盟E選取的L∪{i},上式對于一切聯盟L?N都成立。 當L=N時,則式(12)等于1,因此,式(11)可化簡為: (13) 設D是一個支柱,根據支柱的定義和式(13)可得到 因此有效性公理得到驗證。 驗證可加性:設v,μ,v+μ∈G(N),τ∈gso(N),E?N,根據Choquet積分的性質5, 因此,(v+μ)τ=vτ+μτ -vτ(E{i}))+(μτ(E)-μτ(E{i}))] -μτ(E{i}))=φi(v,τ)+φi(μ,τ) 驗證啞元性:設v∈G(N),τ∈gso(N) D為支柱,D?N,對任意的i∈ND 表明啞元參加到聯盟D中,沒有新的貢獻,因此他能得到保留的收益vτ({i})。 若i不屬于支柱D,對于聯盟E?N,i∈S有 vτ(E∩D)=vτ((E{i})∩D) 將該式代入式(10),有 所有具有灰色授權機制的限制合作博弈的Shapley值滿足啞元性。 以上證明了灰色授權Shapley值滿足合作博弈的四個公理。 假設在某產業集群中企業i=1,2,3協同研制一種復雜產品,企業i生產組件i。由于客觀環境的復雜性、不確定性和技術的局限性,企業3在獨自生產時只能利用其自身0.3的生產能力;而企業3當與企業1組成聯盟時企業3被授予利用?13∈[0.4,0.5]的生產能力;而企業3與企業2組成聯盟時企業3被授予利用?23∈[0.7,0.8]的生產能力;當形成一個大聯盟時3個企業都被授予利用各自的全部生產能力。這種情況可以建立合作博弈模型({1,2,3},v),對于任意的聯盟E?{1,2,3},v(E)表示聯盟E獲得的收益。 v({1})=5,v({2})=6,v({3})=8 v({1,2})=20,v({1,3})=[16,19], v({2,3})=[28,30],v({1,2,3})=60 對于任意的聯盟E?{1,2,3},和i∈{1,2,3},τi(E)表明企業i的生產能力: 表1 企業在不同聯盟中的生產能力 計算限制博弈: vτ({1})=v({1})=5,, vτ({2})=v({2})=6, vτ({3})=v({3})=0.3×8=2.4, vτ({1,2})=v({1,2})=20, vτ({1,2,3})=v({1,2,3})=60。 計算3個企業分別獲得的報酬: 表2 企業3的Shapley值計算 φ3(v?)=[17.25,18.68] 同理可得:φ1(v?)=[16.48,18.75],φ2(v?)=[23.4,25.43]。 根據算例計算出的結果,φ1(v?)+φ2(v?)+φ3(v?)=[57.13,62.89]聯盟支柱的收益v({1,2,3})=60在區間[57.13,62.89]范圍內,所以滿足有效性,φi(v?)>vτ({i}),說明企業通過聯盟合作得到的利益大于企業自己單獨生產所產生的利益,所以分配結果滿足企業形成聯盟合作的個體的合理性。 引入區間灰數來表征企業在聯盟中的參與度和聯盟利益,可以更加直觀的描述因企業自我認識的局限性而造成的對企業在聯盟中的參與度和聯盟利益信息認知的部分明確和部分信息不明確的實際情況。由于區間灰數是一個區間內的某個真值,相比于表達整個區間的區間數,這就降低了在利益分配過程中采用區間數進行分配而帶來的不確定性。其次,應用Choquet積分對具有區間灰數信息的合作能力進行集成,保證了區間灰數的本質特征得以延續,因此也保證了聯盟利益分配的公平性。從計算步驟和計算結果方面分析,本文直接對區間灰數進行計算,有效的避免了因數據處理過程而導致數據不確定性放大或縮小的失真情況。 考慮到在實際的產業集群協同研制過程中企業由于自身技術的局限性,在沒有和其他企業形成聯盟合作時難以發揮出全部的生產能力。因此,本文首先對合作能力信息為灰數的情況,建立了灰色授權算子,其次運用Choquet積分對合作企業之間不完整的依賴關系進行集成,最后將集成信息和Shapley值模型結合起來,建立了具有灰色授權機制的限制合作博弈模型,最后通過應用算例,驗證了模型在產業集群聯盟企業合作中利益分配的公平性和合理性。 本文中,在建立灰色授權機制合作博弈模型時默認了企業之間都是相互促進的關系,然而在實際的產業集群聯盟合作中,企業之間不可避免的會存在一些競爭與沖突關系,如何處理在聯盟合作中企業之間的競爭與沖突關系是今后的研究方向。2.3 Choquet積分
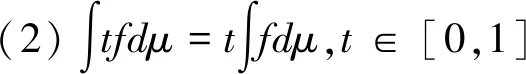
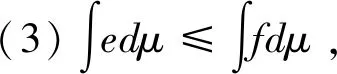
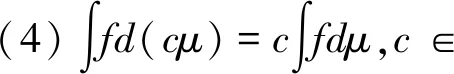
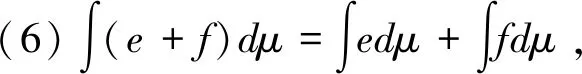
3 構建產業集群聯盟合作的灰色授權機制的Shapley值

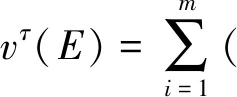

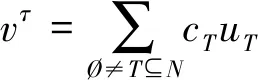
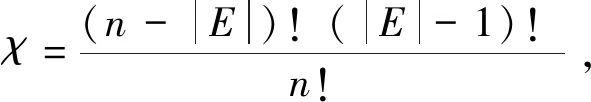
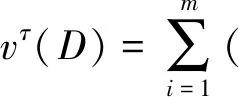
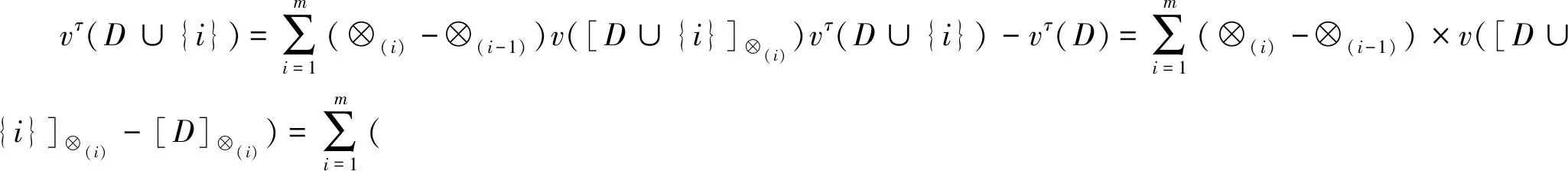
4 應用算例


5 結語

