公路混凝土橋梁疲勞壽命安全評估方法

趙學峰

（山西省交通科學研究院 橋梁工程防災減災山西省重點實驗室，山西 太原 030006）

0 引言

隨著交通運輸業的不斷發展，公路橋梁的安全運輸也成了人們關注的重點，在眾多已建成或正在建設的公路橋梁中，鋼筋混凝土結構占很大比重，因此，對混凝土疲勞壽命的準確評估具有重要的現實意義。多年來，國內外專家學者在結合混凝土的抗疲勞特性、剩余壽命預測等方面，對混凝土的疲勞壽命做出了眾多評估與研究，也取得了許多有學術價值的科研成果，例如彈性力學評估方法[1]。這些方法雖能對混凝土結構材料進行有效的疲勞壽命評估，但偏差值較大，無法對公路橋梁等混凝土結構建筑進行準確的壽命預測，嚴重影響我國交通運輸業的進一步發展。針對上述問題，本文提出并設計了一種基于S-N 曲線的疲勞壽命安全評估方法，并通過實驗論證分析的方式，確定該方法的可行性。結果表明，以鋼筋混凝土的S-N 曲線為基礎，依照線性疲勞損傷累加原則對橋梁疲勞損傷程度進行分析與評估的方式，能夠對公路混凝土橋梁的疲勞使用壽命進行準確評估與預測，較彈性力學評估方法具有極高的有效性。

1 基于S-N 曲線的混凝土橋梁疲勞壽命評估方法設計

1.1 構建S-N 曲線

為了準確評估混凝土結構的疲勞強度和使用壽命，本次設計引入外荷載與疲勞壽命之間的關系理論，建立能夠反映混凝土應力幅值和疲勞使用壽命之間關系的曲線，這條曲線就叫做S-N 曲線[2]，如圖1 所示。

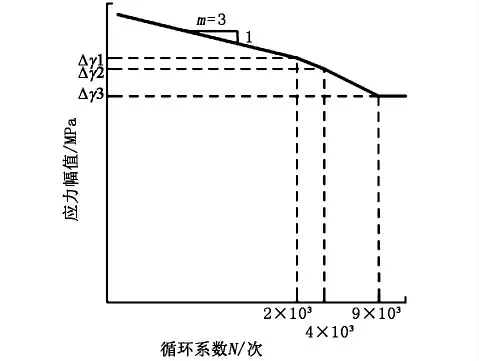
圖1 混凝土S-N 曲線示意圖

圖1中，x 軸和y 軸均采用對數坐標，其方程表達式為：

式中：Δγ 代表混凝土的實際應力幅值；m 代表S-N曲線斜率；C 為常數，本次計算不做定向分析。

斷裂力學的研究表明，在橋梁表面已經產生裂紋的情況下，小于Δγ 的應力幅值也會加大裂紋擴展面積[3]。因此本次設計將S-N 曲線的斜率調整為m+2，若實際應力幅值高于Δγ，則此時混凝土為疲勞狀態，橋梁趨于不穩定狀態；反之，若實際應力幅值低于Δγ，則此時混凝土結構不會產生疲勞損傷，橋梁將具有無限安全壽命。

1.2 臨界裂紋尺寸確定

在上述構建的S-N 曲線內，對混凝土的裂紋過程進行模擬。首先通過無損檢測方法對混凝土的裂紋形狀和位置進行檢測，然后根據理想化裂紋結構確定初始裂紋的簡化結構[4]，在此基礎上，對混凝土的裂紋結構進行描述并建立基本假定。

若實際裂紋尺寸大于初始裂紋結構時，即K≥K0，則根據S-N 曲線的力學發展，對混凝土橋梁發生脆性斷裂的可能性進行計算，可得到混凝土結構臨界裂紋的深度為：

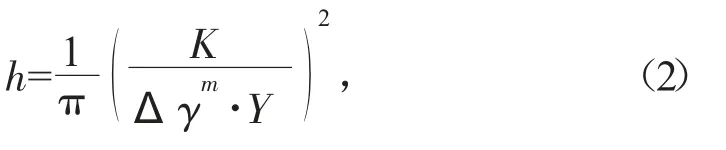
式中：h 代表橋梁的臨界裂紋深度；Y 代表應力強度因子。

若混凝土發生韌性斷裂時，其橫截面會大幅增加，同時，裂紋尺寸也會增大。當承受外荷載的橫截面面積隨著斷裂強度的增加而減小時，斷裂橫截面上的應力幅值將會增大并達到最大。這一過程中，忽略其他外力作用，理想狀態下認為初始缺陷截面所受到的作用力與臨界裂紋截面所受到的作用力相等。則根據混凝土結構發生斷裂時受到的合力，計算裂紋的半長度為：

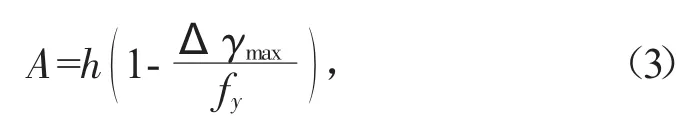
式中：A 代表混凝土裂紋半長度；fy代表裂紋拓展后的界面應力幅值；Δγmax代表作用在斷裂混凝土結構上的最大應力值。

得出混凝土結構的裂紋半長度后，相對應的加上整個混凝土結構的總長，便可得到臨界裂紋的具體尺寸，為下一步的安全評估計算做準備。

1.3 混凝土結構疲勞壽命評估計算

研究發現，在應力幅值作用下混凝土橋梁的使用壽命是由橋梁內部的受力情況決定的[5]，因此疲勞壽命安全評估的過程可以轉化為在隨機變動應力幅值的條件下，混凝土的裂紋擴展面積的計算過程。根據Paris 應力強度理論，設計如圖2 所示的評估模型。

將應力強度因子的變化幅值作為描述混凝土疲勞荷載的特征性，結合圖2 模型，計算其裂紋擴展面積[6]，在S-N 曲線坐標系下，裂紋擴展速率與應力強度因子的對應關系為：

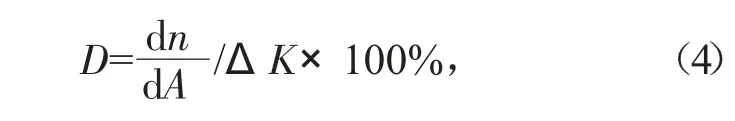
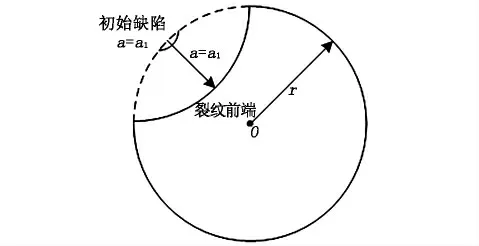
圖2 基于S-N 曲線的混凝土疲勞分析模型

式中：D 代表混凝土裂紋的擴展速率，用百分比計量；n 代表混凝土結構常數；ΔK 代表裂紋均值。

分析式（4）可知，對于任意一個應力幅值，都有一個循環次數Δn 與之相對，若混凝土結構發生缺陷時，相對應的應力強度幅值不變，則必定存在一個與應力幅值相關的強度因子。只有保證應力強度因子幅值低于初始值，才能將混凝土結構的損壞情況加以制止。

由于S-N 幾何修正因子是不斷變化的，因此采用循環計算方法[7]，對每一層結構的應力幅值進行確定。假設裂紋的半長度為A1，相對應的強度因子幅值為ΔKm，實時監測橋梁的缺陷情況，并記錄每個循環因子的應力幅值，計算對應的裂紋增量為：

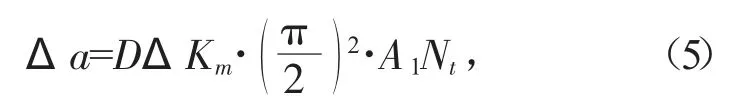
式中：Δa 代表橋梁的裂紋增量，即裂紋拓展面積；Nt代表t 時刻內產生的缺陷面積。

已知橋梁的裂紋拓展面積越大，疲勞壽命的安全使用周期越長；反之，若橋梁的裂紋拓展面積越小，疲勞壽命的安全使用周期越短。則根據上述分析，能夠實現對公路混凝土橋梁疲勞壽命安全的準確評估，但由于計算裂紋擴展面積時，需要反復計算裂紋擴展增量Δa，導致評估工作量過大，影響評估效率。因此本次計算采用C+語言程序[8]，將公路混凝土橋梁的初始缺陷長度、臨界裂紋尺寸、應力強度因子幅值、材料斷裂常數等參數均輸入程序，采取均值參考系數的方法，對混凝土結構的疲勞壽命進行評估計算。

從混凝土結構裂紋萌生開始，向程序內輸入初始裂紋長度，經過不同應力幅值的循環作用，對裂紋擴展增加面積進行計算，直至累加的應力幅值達到臨界裂紋尺寸，這時混凝土結構將發生斷裂，停止使用，那么致使混凝土發生斷裂的最大應力幅值就是此次循環結構的疲勞剩余壽命。至此，完成對基于S-N曲線的公路混凝土橋梁疲勞壽命安全的評估計算。

2 實驗分析

為保證本文設計的基于S-N 曲線的公路混凝土橋梁疲勞壽命評估方法的可行性與有效性，對某混凝土橋梁進行疲勞生命安全的評估。該橋梁主梁為空心板，主梁混凝土結構標號為C50，橋面混凝土標號為C50，主筋直徑為20 mm，斜向跨徑為10 m，梁高為0.5 m，斜交角度為40°。同時，為了保證實驗結果更具說明性，采用彈性力學評估方法與本文S-N 曲線評估方法進行對比，具體實驗過程及結果分析如下。

2.1 基于S-N 曲線的橋梁壽命評估實驗

由于橋梁受力的不均衡性，因此在車輛荷載作用下，混凝土結構逐漸發生裂紋現象，但這一過程中，無法直接獲取裂紋截面的應力幅值，故本次實驗假設混凝土結構處于彈性階段，發生裂紋時，截面應力服從理想狀態下的裂紋應力。同時，認為混凝土之間沒有滑移作用，不產生其他阻力，根據裂紋截面的應力幅值，得到受力混凝土結構的應力過程。

橋梁結構中，考慮到鋼筋腐蝕疲勞的影響，根據上述過程，計算混凝土結構的疲勞極限值與應力強度因子，并將結果代入式（5），得出其疲勞壽命的評估值，具體結果如表1 所示。

2.2 基于彈性力學的橋梁壽命評估實驗

彈性力學評估實驗首先要準確測量橋梁的各個參數值，也正由于此過程的復雜程度，導致最終的評估結果偏差項過大。

參考前人的研究成果，將各個計算結果代入彈性力學評估模型中，判斷混凝土應力強度因子的幾何修正系數和裂紋擴展情況。若應力強度因子的幾何修正系數低于初始強度值，則認為該結構存在裂紋，通過模型計算其疲勞壽命；若應力強度因子的幾何修正系數高于初始強度值，則說明該混凝土結構性能良好，其剩余疲勞壽命約為50年，因此不做計算。在認為本次實驗過程中混凝土結構存在裂紋的前提下，得到的疲勞壽命評估結果如表1 所示。

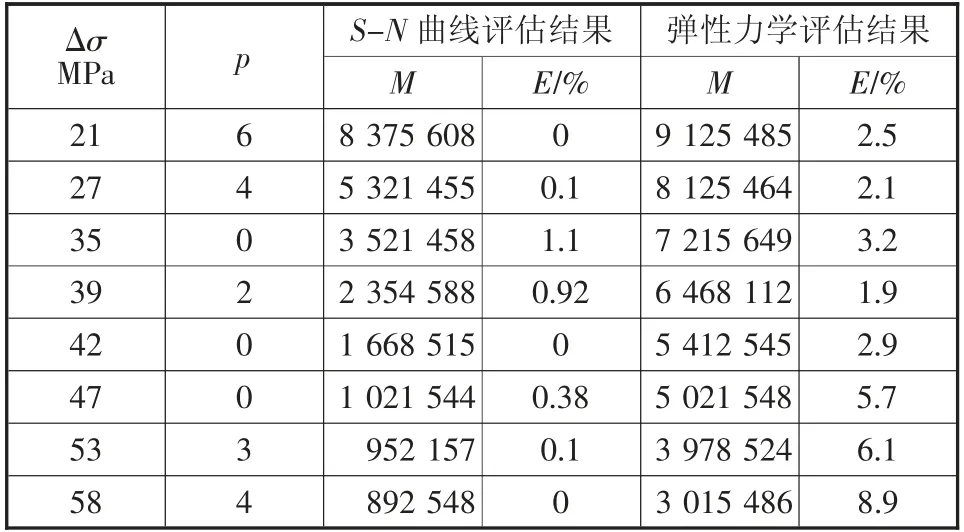
表1 橋梁疲勞壽命評估結果對比表

2.3 結果分析

根據上述兩種不同方法對橋梁的疲勞壽命進行評估，得到的評估結果如表1 所示。

表1 中，Δσ 代表實驗過程中混凝土所受應力幅值水平；p 代表各級應力幅值的循環次數；M 代表混凝土實際疲勞損傷評估值；E 代表評估偏差項。

分析表1 實驗結果可知，采用彈性力學與S-N曲線均能完成對公路混凝土橋梁疲勞壽命安全的評估，但實際疲勞損傷估計值的大小和偏差項不同。分析可知，基于彈性力學的評估方法對橋梁疲勞壽命的估計損傷值偏高，偏差項百分比過大；而本文基于S-N 曲線的評估方法下，對橋梁疲勞壽命的損傷評估值也略高一些，但不影響最終評估結果的分析，且平均偏差項僅為0.65%，不影響實際評估結果，因此可以確定本文評估方法的有效性和可行性。結果表明，基于S-N 曲線的公路混凝土橋梁疲勞壽命安全評估方法，能夠在不對混凝土結構產生疲勞損傷的前提下，對其疲勞使用壽命進行準確評估與預測。

3 結語

通過上述論證，將基于S-N 曲線的橋梁疲勞壽命評估方法進行一次推演，通過計算裂紋的臨界值，準確判定橋梁的疲勞壽命。希望在今后的橋梁安全評估中充分應用該方法，并進一步保障公路混凝土橋梁的安全，為我國交通運輸行業的發展奠定基礎。