小型混合翼無人機過渡過程一體化建模與控制
王博豪 張 勇 徐偉程 郭 錦
(1.南京航空航天大學自動化學院,南京 210016;2.南京航空航天大學無人機研究院,南京 210016;3.中小型無人機先進技術工業和信息化部重點實驗室,南京 210016)
1 引 言
當下無人機發展勢頭迅猛,無人機按照飛行平臺機構可分為固定翼無人機、旋翼無人機、無人飛艇、傘翼無人機、撲翼無人機等[1]。其中近年來固定翼無人機和旋翼無人機因飛行特性好、穩定性高發展尤為迅速。多旋翼無人機前飛速度較慢,而且由于現有電池容量有限,航程和航時受到限制。固定翼無人機擁有較快的前飛速度,固定翼無人機航時和航程是多旋翼無人機的二到三倍,但是起飛和降落一般采用滑跑起飛的方式,在應用時往往會受到場地的影響而無法使用。
為解決固定翼無人機和旋翼無人機的缺點,混合翼垂直起降無人機應運而生。混合翼垂直起降無人機相對傾轉旋翼無人機具有結構簡單的特點,只需要在原來固定翼結構上加裝旋翼部分即可。對復合式垂直起降無人機過渡過程定性的建立了六自由度動力學方程,提出了一種過渡方案,對一些典型的技術問題,提出了相應的對策;對旋翼和固定翼分別建模,采用旋翼只提供升力不產生力矩的控制策略,為保證無人機姿態讓無人機總升力與重力相等,僅通過控制固定翼的舵面控制無人機姿態,但由于轉換初期速度較低,機翼尾翼調整能力有限,旋翼提供升力不產生力矩,導致前期姿態波動較大;對垂直起降模式和固定翼模式分別建模,在過渡過程起始階段僅依靠旋翼部分提供前飛和保持姿態穩定,在達到合理的速度后直接切換為固定翼模式,但旋翼和固定翼為兩個完全不同的模型,直接切換會使系統輸入和狀態量產生突變,無法保證系統的穩定性。本文在過渡過程中旋翼部分和固定翼部分同時對無人機施加力和力矩,將旋翼部分和固定翼部分進行整體建模,建立了過渡過程旋翼和固定翼共同控制無人機狀態的六自由度模型,然后對縱向運動模型進行配平和小擾動線性化,并對得到的縱向過渡過程模型進行穩定性分析,最后設計了基于增益調度的LQR全狀態反饋控制器。通過仿真驗證,所設計的控制器能夠滿足設計要求。
2 數學建模
由于旋翼部分和固定翼部分的控制面和系統輸入均不同,導致兩模型差異較大。在前飛速度增大的轉換過程中,切換兩個模型會使無人機狀態發生突變,無法保證無人機的穩定性。將旋翼和固定翼整體建模,讓旋翼和固定翼共同控制無人機姿態,使過渡過程更加平緩,并保證過渡過程的穩定性。
混合翼垂直飛降無人機試驗樣機如圖1所示。

圖1 混合翼垂直起降無人機試驗樣機Fig.1 Hybrid wing vertical take-off and landing unmanned aircraft test prototype
對于無人機平動有
(1)

將上式展開得
(2)
式中:Fx、Fy、Fz——分別為無人機在機體坐標系下沿機體軸方向受力的分量;u、v、w——分別為沿機體坐標軸方向上的速度分量;p、q、r——分別為沿機體坐標軸各方向上的角度分量。
(3)
式中:Ffx、Ffy、Ffz——分別為固定翼在機體軸三個方向上的分力;Fxz、Fyz、Frz——分別為旋翼在機體軸三個方向上產生的升力[6]。
對于無人機繞質心的運動有
(4)
(5)
式中:L、M、N——無人機受力矩在機體坐標軸上的投影;J——慣性矩陣。
(6)
式中:lf、mf、nf——分別為固定翼產生的滾轉、俯仰、偏航力矩;lr、mr、nr——分別為旋翼產生的滾轉、俯仰、偏航力矩。
過渡過程縱向運動方程組為
(7)
(8)
(9)
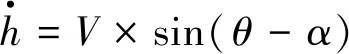
(10)
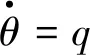
(11)
式中:T——固定翼推力;D——無人機所受阻力;α——迎角;θ——俯仰角;V——慣性坐標系前飛速度。
復合式垂直起降無人機的前飛速度是過渡過程中的重要特征參數,無人機過渡過程前飛速度由0加速,加速到固定翼起飛速度即18m/s,隨著速度的增大,固定翼機翼產生的升力越來越大,需要給定相應的旋翼油門保持合理的飛行姿態。將縱向運動方程組在速度V=[0,18]m/s范圍內進行配平,并對配平狀態進行線性化,線性擬合得到關于前飛速度V的狀態空間表達式
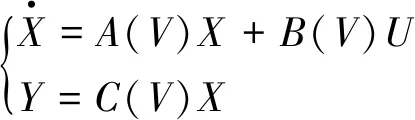
(12)
系統狀態X=[Vαqhθ],輸入U=[teT1T2]。其中t為固定翼油門,e為升降舵輸入,T1、T2分別為前邊一對和后邊一對的旋翼油門。
由圖2可以看出,在前飛速度V=[0,18]m/s范圍內,系統存在實部大于0的特征根,即在速度變化過程中存在不穩定狀態。不同前飛速度系統狀態相差較大,傳統的線性時不變控制器無法得到滿意的控制效果。

圖2 不同狀態下系統特征根在復平面分布Fig.2 Distribution of the eigenvalues of the system in the complex plane under different states
3 控制器設計
由以上對系統特征值分析可知,單一的線性控制器無法使系統在參數進行大范圍變化時得到良好的跟蹤效果。采用基于LQR的增益調度策略設計控制器,將系統參數變化較大的非線性系統分成多個部分,降低系統參數的變化范圍,然后在各部分進行配平和線性化,得到相應的線性時不變系統,針對各個線性時不變系統設計LQR控制器。線性時不變控制器能夠在一定范圍內對非線性系統進行良好的控制,根據非線性系統的參數變化,來切換相應的線性控制器,從而控制整個非線性系統[7~10]。
對于各部分能控能觀線性系統,其狀態方程有如下形式
(13)
式中:X∈Rn——n維狀態向量;Y∈Rm——m維輸出向量;U∈Rr——r維控制向量;A0,B0,C0,D0——分別為n×n維,n×m維,m×n維,m×r維常數矩陣[11]。
為使前飛速度和高度跟蹤指令信號,令前飛速度和高度輸出y=(V,h)和指令信號yr=(Vr,hr)的誤差為
e=yr-y
(14)
設計能量函數J
(15)
式中:Q、R——分別為n×n維,m×m維對角矩陣;Q——半正定矩陣;R——正定矩陣。目標函數的意義在于使用較小的輸入量使得系統的狀態量有盡可能小的誤差,所以當取得能量函數J最小時,目標成立[12~14]。
為了讓能量函數最小,需要引入λ構造Hamilton函數
(16)
通過解Riccati方程和n維向量得
(17)
(18)
系統的輸入為
(19)
則狀態反饋增益矩陣可以表示為
(20)
系統最優跟蹤軌跡線是以下微分方程的解
(21)
以前飛速度V=15m/s,高度h=10m為例,對系統進行配平和小擾動線性化,得到無人機在該狀態下的縱向系統狀態空間矩陣
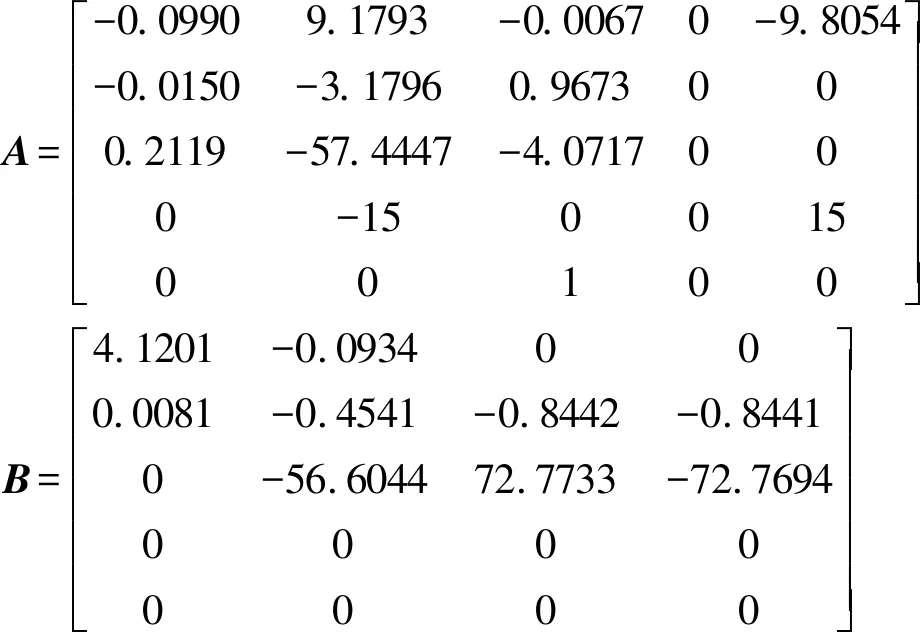
選取控制系統狀態有關的權重矩陣Q=diag(1,1,1,1,1),和系統輸入有關的權重矩陣R=diag(1,1,1,1),通過計算得到系統的反饋增益K

同理,為使過渡過程相對平滑,在定高狀態下,選取前飛速度為3m/s,6m/s,9m/s,12m/s,15m/s,作為無人機工作點進行配平。在各配平點采用設計相應的控制器。通過切換控制器來實現以前飛速度為參考的增益調度。控制結構如圖3所示。

圖3 控制器結構Fig.3 Controller structure
系統初始狀態X=[0;0;0;10;0]。前飛速度設定為斜率為3的斜坡信號,達到18m/s時保持。系統仿真結果如圖4~圖6所示。由下圖可以看出,在加速階段無人機前飛速度可以在各速度下得到不錯的跟蹤效果,在8s和10s時加入階躍輸入,同樣可以得到良好的跟蹤效果。無人機縱向高度在加速階段會出現掉高,在第12s加入階躍信號,無人機高度有一定的超調,沒有靜態誤差。
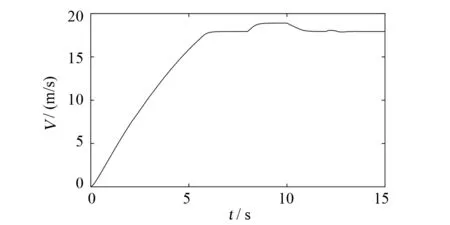
圖4 混合翼無人機過渡過程速度隨時間響應曲線Fig.4 Velocity response curve of hybrid wing UAV in transition process
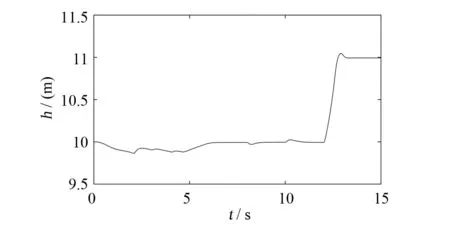
圖5 混合翼無人機過渡過程高度隨時間響應曲線Fig.5 Height response curve of hybrid wing UAV in transient process
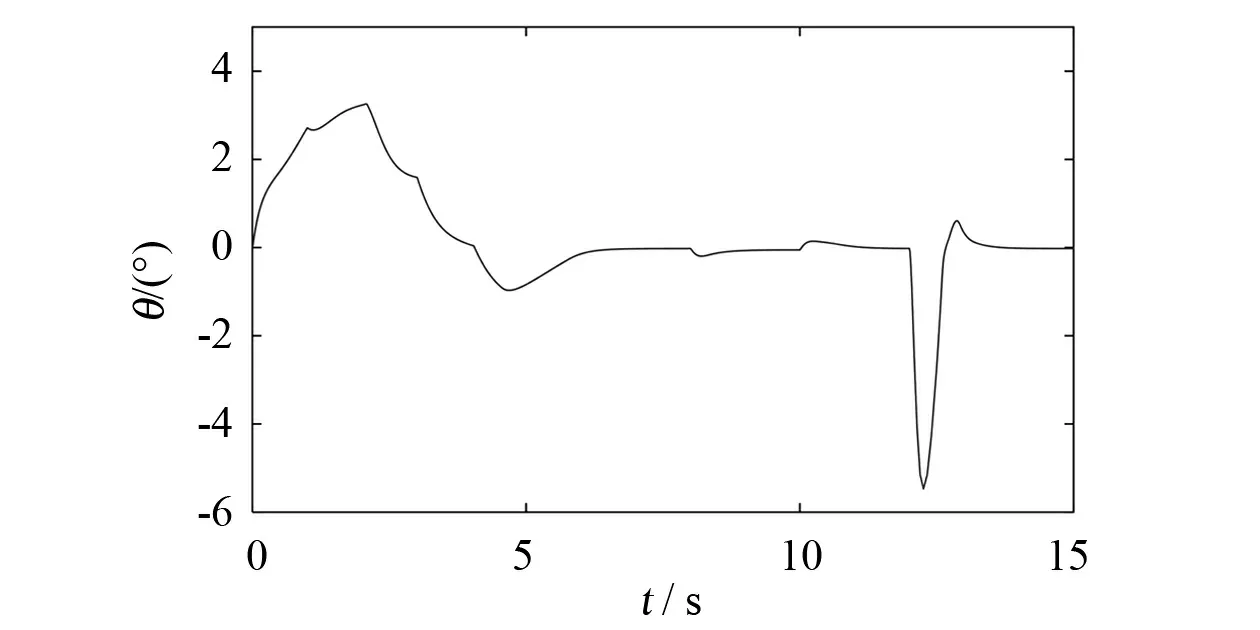
圖6 混合翼無人機過渡過程俯仰角隨時間響應曲線Fig.6 Pitch angle Height response curve of hybrid wing UAV in transient process
4 結束語
本文對小型混合翼垂直起降無人機的過渡過程進行了一體化整體建模,推導了六自由度非線性動力學方程,進行配平和小擾動線性化,對得到的數學模型進行穩定性分析。采用基于LQR的增益調度控制,對無人機的速度和高度進行跟蹤控制,有仿真結果可知前飛速度在加速和勻速階段都有良好的跟蹤效果。無人機在前飛加速過程高度有約0.2m的掉高,且在跟蹤過程中存在超調。俯仰角在加速階段波動較大,需要改進控制方法,改善高度和俯仰角的控制效果。

