全相位FFT頻率測量在調頻激光測距技術中的應用

郭天茂 劉 柯 繆寅宵 宋金城 郭力振 王曉光

(北京航天計量測試技術研究所,北京 100076)

1 引 言

調頻連續波(Frequency Modulated Continuous Wave,FMCW)激光測距技術是一種近距離高精度絕對測距技術，具有非合作、非接觸等優點，在火箭裝配誤差測量[1]、風電葉片面型測量等高精度大尺寸三維形貌測量領域的應用具有重要意義。在FMCW激光測距中，調制信號源通過產生三角波信號對可調諧激光器進行調制，使出射激光的光頻周期性線性變化，激光發射信號與經目標反射返回的回波信號混頻后得到中頻信號，測量中頻信號的頻率即可反推出被測目標到探測器之間的距離信息。因此，在FMCW激光測距技術中，對于距離信息的解算實質上就是對中頻信號頻率的解算。

傳統上，對數字信號進行快速傅里葉變換(FFT)是我們獲取其頻率的主要方法，但是傳統的FFT頻率分辨率較低，因此我們需要在傳統FFT的基礎上對信號進行頻譜細化，提高頻率分辨率。目前常用的頻譜細化方法主要有直接抽取法、級聯FFT法、頻域增采樣法、時域補零法、Chirp-Z變換法和ZFFT變換法等[4]。但是這些方法都是在傳統FFT的基礎上進行的，實質細化精度并沒有突破傳統FFT的限制。并且傳統FFT運算過程中需要對信號進行截斷，由此會引發頻譜泄露。針對上述問題，文獻[3]提出了全相位FFT(all-phase FFT, ap-FFT)算法，這種算法能夠有效抑制頻譜泄露，并且具有相位不變性。相位不變的特性對于基于時移相位差的頻率計算是非常有利的，利用相位與頻率之間的關系，我們就可以研究兩個存在時移關系的序列，利用兩個序列頻域上主譜線的相位差校正出準確頻率。本文利用基于全相位FFT譜分析的時移相位差頻譜校正法實現調頻激光測距中的中頻信號的頻率估計。

2 調頻連續波激光測距技術簡介

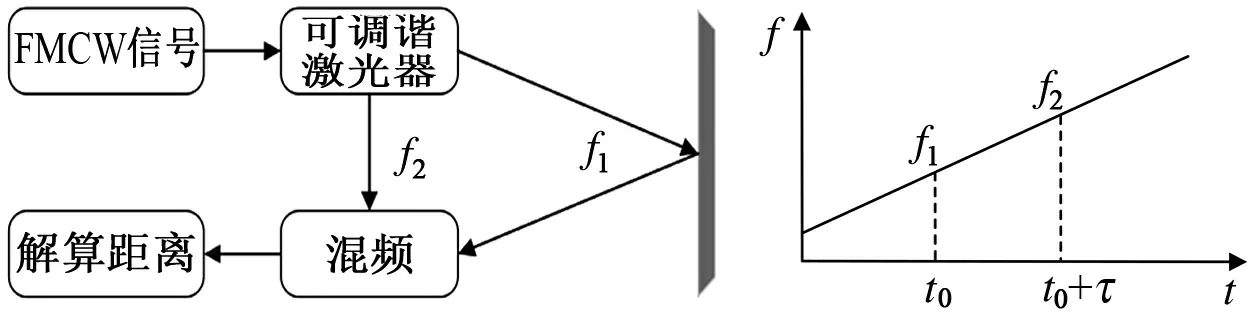
圖1 調頻連續波激光測距原理示意圖Fig.1 Schematic diagram of FMCW laser ranging

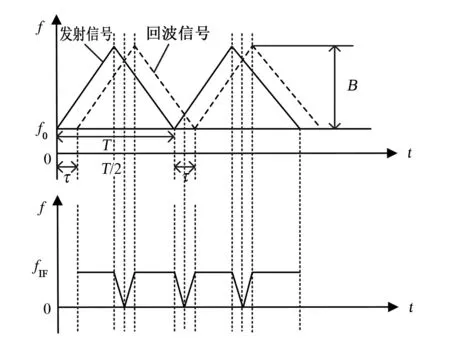
圖2 線性調頻連續波信號處理原理Fig.2 Schematic diagram of FMCW Signal Process

(1)

(2)

式中：c——光速;R——測距系統與目標之間的距離值，根據公式(1)和公式(2)可得

(3)

由上式可知，通過測量包含目標距離信息的中頻信號的頻率，即可準確提取出目標的距離信息。

3 基于全相位FFT譜分析的時移相位差頻譜校正法

在全相位FFT算法中，首先需要對輸入序列進行全相位預處理，之后再對處理之后的序列進行傳統FFT運算。全相位FFT與傳統FFT存在許多相似的性質，如齊次性、疊加性、時不變性、頻移性等，因此可采用與傳統FFT相同的方法對全相位FFT生成的頻譜進行處理。全相位FFT的預處理與運算過程如圖3所示。

圖3 全相位FFT頻譜分析流程(N=4)Fig.3 Flow diagram of ap-FFT Spectrum analysis(N=4)

序列ωc是兩個長度為N的數字序列的卷積，兩個序列分別稱為前窗f與后窗b，則有公式(4)

wc(n)=f(n)×b(-n)-N+1≤n≤N-1

(4)

當f和b均為矩形窗時，則稱為無窗全相位預處理；當f和b其中之一為矩形窗時，則稱為單窗全相位預處理；當f和b均不是矩形窗時，則稱為雙窗全相位預處理[6]。其中，雙窗全相位預處理抑制頻譜泄露的性能最好。因此，對信號進行雙窗全相位預處理。

下面介紹在全相位FFT的基礎上實現時移相位差頻譜校正的算法。

假設單頻信號的復指數序列為

{x(n)=ej(ω*n+θ0)|n∈[-N+1-L,N-1-L]}

(5)

延時n0個點之后的序列為

{x(n)=ej(ω*(n-n0)+θ0)|n∈[-N+1-L,N-1-L]}

(6)

序列(5)的雙窗全相位FFT譜分析的表達式為

(7)

根據全相位FFT的相位不變性，其主譜線k*上的相位譜為

φ1(k*)=θ0

(8)

根據全相位FFT的線性性質，延時后的序列(6)的頻譜表達式為

(9)

則其主譜線k*上的相位譜表達式為

φ2(k*)=θ0-ω*n0

(10)

取式(8)和(10)之間的差值，有

Δφ=φ1(k*)-φ2(k*)=ω*n0

(11)

由公式(11)可以看出，具有時移關系的兩序列的主譜線的相位差Δφ與延時大小n0成正比，當n0變大時，Δφ也跟著變大。但是受觀測范圍的限制，主譜線的相位φ1(k*)與相位φ2(k*)的范圍均為(-π, π)，則Δφ的取值范圍為

-2π≤Δφ≤2π

(12)

此時測得的相位值與實際相位值是不同的，這種現象稱作“相位模糊”。需要對相位差進行補償以消除“相位模糊”。相位補償值的計算方法為：主譜線k*對應的數字角頻率為2k*π/N，經過n0延時后，會引起2k*πn0/N的附加相移。所以，2k*πn0/N就是相位補償值。從而有

Δφ=φ1(k*)-φ2(k*)+2k*πn0/N=ω*n0

(13)

則補償后的頻率估計為

ω*=[φ1(k*)-φ2(k*)]/n0+2k*π/N

(14)

全相位時移相位差法的頻率校正流程圖如圖4所示[3]

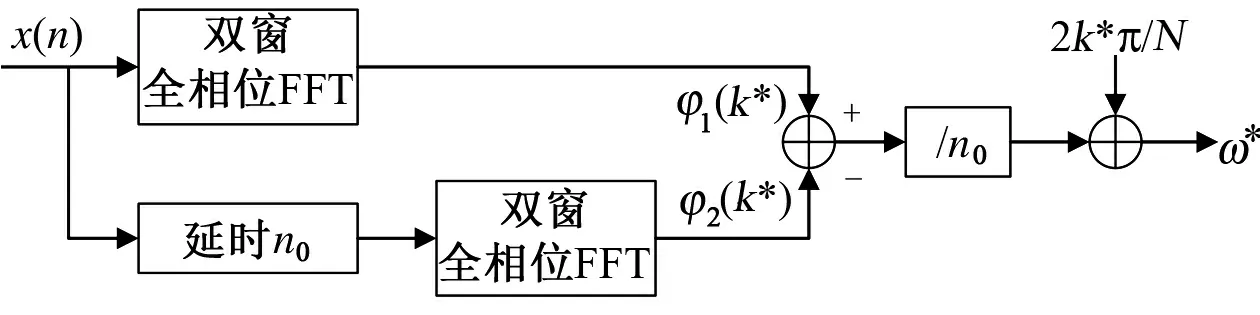
圖4 全相位時移相位差法頻譜校正流程Fig.4 Spectrum correction process flow diagram of all-phase time-shift phase difference method

可見，前后兩段序列的初始相位差值除以延時點數n0就可以得到頻偏值，相位補償值與n0的比值為主譜線的頻率，二者相加即可得到輸入信號的頻率估計值。由以上分析可知，在單頻信號頻率的測量過程中，相位補償值是確定的，并且由于全相位FFT的相位不變性，相位差的估計也是準確的，因而由公式(14)得到的頻率估計值也是準確的。

4 試驗驗證

4.1 測距試驗

項目中搭建了調頻激光測距系統，利用長導軌進行試驗，對由近及遠的標準位移進行測量，采集數據，在MATLAB環境下進行頻率解算獲得距離值，對全相位時移相位差法在調頻激光測距中的應用效果進行驗證，同時與傳統FFT時移相位差法進行對比。

試驗參數如下：

采樣頻率：100MHz；

FFT點數：4096；

時移點數：4096；

采樣位寬：14位；

apFFT預處理：采用雙窗預處理。

表1為部分測量數據。

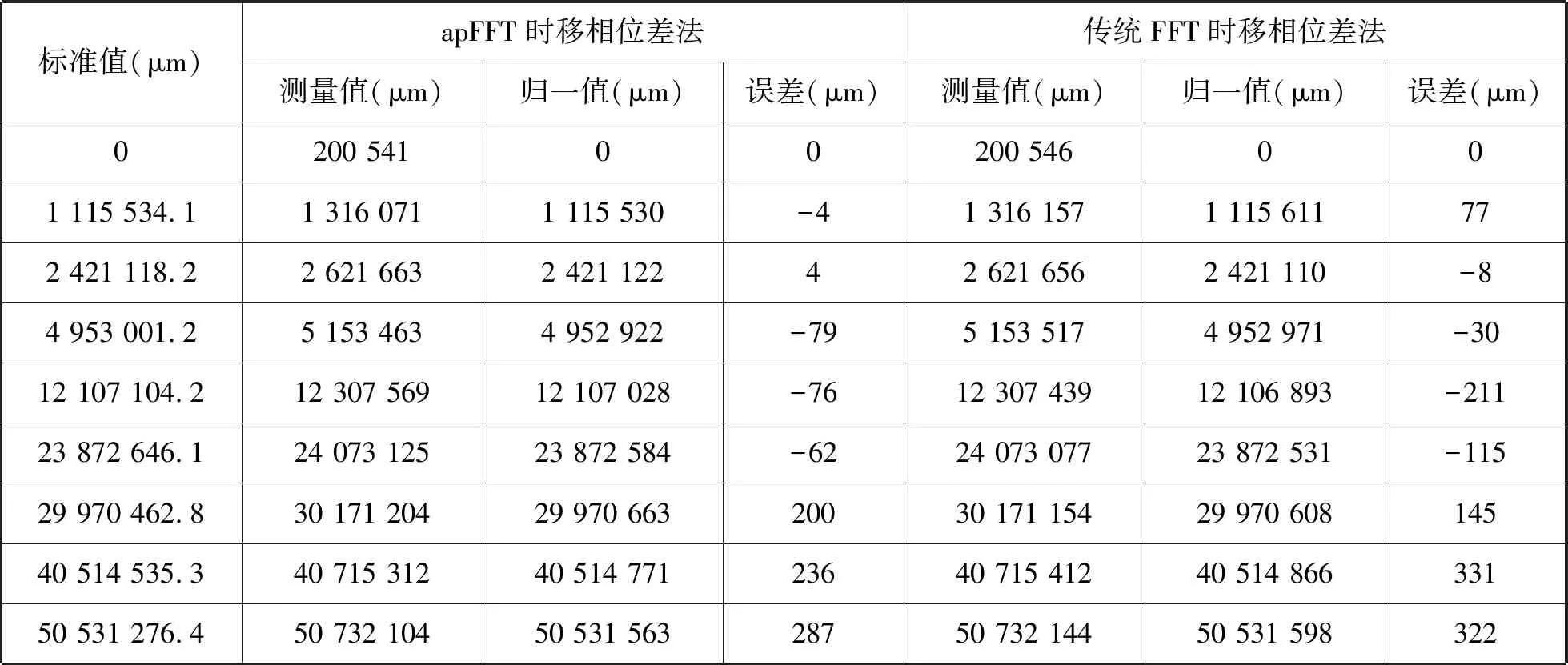
表1 試驗測量結果Tab.1 Result of the measurement

由于測距系統未放置于導軌的初始零點處，因此試驗過程中測得的距離值與標準值總是存在一個固定的差值。由表1可以看出，測距系統的測量誤差隨著距離的增大而增大，這是由于隨著距離變遠和電路噪聲的引入等導致回波信號的信噪比變差，相位提取不準確導致的。利用此方法對回波信號進行處理，在超過50m距離處測量誤差不超過0.3mm。可見基于全相位時移相位差頻譜校正法的頻率估算方法在調頻連續波激光測距中具有良好的應用效果。

通過對比可以看出，基于傳統FFT的時移相位差法的測量誤差明顯大于apFFT法，但是在某些距離上二者的誤差相差不大，這是由時移相位差法本身的原理決定的，由第3章的原理介紹可知，在時移相位差法中，相位差的組成包括兩部分：頻譜上直接提取的相位差和補償的相位差。在調頻連續波激光測距系統中，采樣頻率為100MHz，FFT計算點數相對于采樣頻率來說并不算大，因此柵欄效應明顯，不管是apFFT還是傳統FFT，二者提取到的主譜線的位置幾乎相同，因此二者的相位補償值相同。但是apFFT對相位的提取比傳統FFT準確，因此由基于apFFT的時移相位差法提取到的頻率值比基于傳統FFT的時移相位差法要準確，進而前者的測量誤差也要明顯小于后者。

4.2 全相位FFT方法中計算參數對頻率測量的影響

我們利用在距離值約為5m、10m和20m時分別采集的1000組測量數據，改變計算過程中FFT的運算點數和時移點數，探究二者對頻率測量的影響。

4.2.1 FFT運算點數對頻率測量的影響

將時移點數固定為4096，改變FFT的運算點數，頻率測量值如表2所示。

表2 試驗測量結果Tab.2 Result of the measurement

由表2數據可以看出：①在同一距離值處，當FFT點數增加時，計算結果的標準差和極差值趨于減小，穩定性增加，計算偏差減小；② 當運算點數固定時，隨著距離值的增加，計算結果的標準差和極差值都趨于增大，穩定性降低，計算偏差增大，這也與4.1條測距試驗中距離測量結果的誤差變化趨勢相吻合。

分別對相同運算點數下不同距離的頻率測量平均值做差，得到表3中的數據。

根據表3中的數據，運算點數為1024和2048時，5m～10m之間的頻率差相差約4.8kHz，10m～20m之間的頻率差相差約2.4kHz；運算點數為2048和4096時，5m～10m之間的頻率差相差30Hz，10m～20m之間的頻率差相差10Hz。隨著點數的增加，對應固定距離的測量，頻率差逐漸趨于穩定。

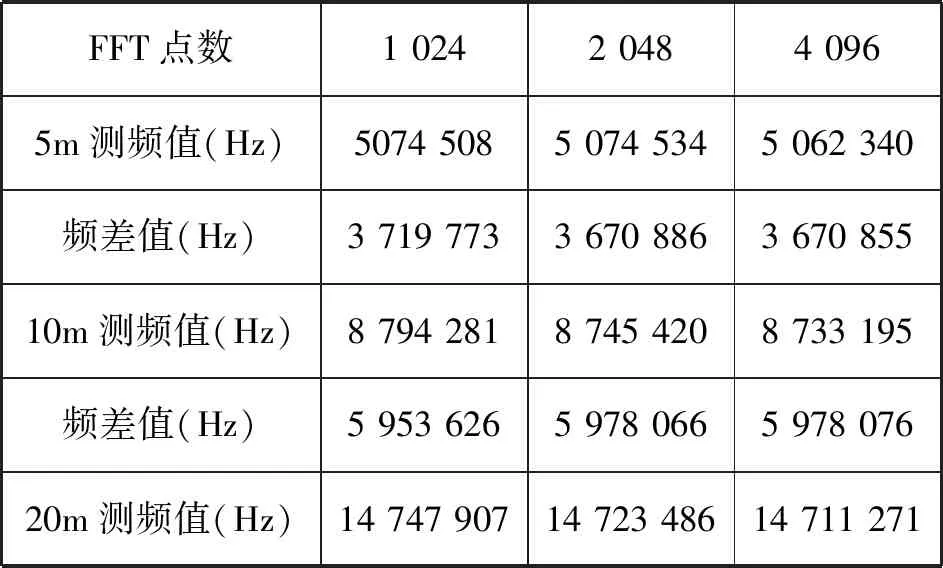
表3 不同距離之間的頻率差Tab.3 Frequency difference between different distances

4.2.2 時移點數對頻率測量的影響

將FFT的運算點數固定為4096，改變時移點數時，頻率測量結果如表4所示。

表4 試驗測量結果Tab.4 Result of the measurement

由表4數據可以看出：①在同一距離值處，當時移點數增加時，計算結果的標準差和極差值趨于減小，穩定性增加，計算偏差減小；②當時移點數固定時，隨著距離值的增加，計算結果的標準差和極差值都趨于增大，穩定性降低，計算誤差增大。

如4.2.1條，分別對相同時移點數下不同距離的頻率測量平均值做差，得到表5中的數據。

表5 不同距離之間的頻率差Tab.5 Frequency difference between different distances

時移點數為1024和2048時，5m～10m之間的頻率差相差約48kHz，10m～20m之間的頻率差相差7Hz；運算點數為2048和4096時，5m～10m之間的頻率差相差12Hz，10m～20m之間的頻率差相差6Hz。隨著時移點數的增加，不同距離間的頻率差逐漸趨于穩定。

4.2.3 結論

根據以上的試驗數據可知，增加FFT運算點數和時移點數有助于提高頻率測量結果的準確性和穩定性，但是FFT運算點數提高到一定范圍之后對測量結果的影響會逐漸減小。增加FFT運算點數會導致硬件開銷大大增加，運算效率降低。因此在實際應用過程中，應根據試驗和仿真情況酌情選擇合適的FFT運算點數和實際情況允許下最大的時移點數。

5 結束語

調頻連續波激光測距技術具有測量距離遠、測量精度高和不需要合作目標等優點，與其他常見的非合作激光測距體制相比具有最高的測量精度。將全相位時移相位差法應用于調頻連續波激光測距技術，達到了較高的距離測量精度。探討了在全相位時移相差法中計算參數對測量結果的影響，提高FFT運算點數和時移點數都能夠提高測量的準確性和穩定性，然而為了兼顧計算效率，不應該一味提高運算點數。事實上，只有將數字信號處理技術與FPGA相結合才能達到實際應用的要求，這也是本文后續的研究目標。