基于夾層板理論的圓形孔蜂窩結(jié)構(gòu)隔聲量研究

李志寬，吳錦武，田文昊，李 威

(南昌航空大學(xué)飛行器工程學(xué)院，江西 南昌 330063)

0 引 言

蜂窩夾層結(jié)構(gòu)主要由上下面板和蜂窩層芯組成，由于該類結(jié)構(gòu)具有高強(qiáng)度比、高剛度比和質(zhì)輕等優(yōu)點(diǎn)，廣泛應(yīng)用于飛行器、船舶、高速列車[1-3]等交通工具。對(duì)蜂窩結(jié)構(gòu)的研究，主要集中在芯層為正六邊形結(jié)構(gòu)的蜂窩，而對(duì)圓形孔蜂窩結(jié)構(gòu)研究甚少。圓形蜂窩結(jié)構(gòu)有芯材耗量少、強(qiáng)度比高、承載力更高等特點(diǎn)，同時(shí)可避免多邊形孔角部的應(yīng)力集中[4-5]。

對(duì)蜂窩夾層板結(jié)構(gòu)的隔聲性能研究，需先分析夾層板結(jié)構(gòu)振動(dòng)特性，由于蜂窩夾層結(jié)構(gòu)層芯在受力時(shí)的離散非均勻性[6]，通常將結(jié)構(gòu)等效為均質(zhì)正交各向異性板，尤其以三明治夾層板理論精度最高[7]。LIN等[8]基于應(yīng)變能法得到了圓形孔蜂窩層芯面內(nèi)彈性參數(shù)，但尚未對(duì)蜂窩層芯的面內(nèi)等效剪切彈性參數(shù)給出具體公式。BACKSTR?M等[9]基于四階梁理論評(píng)估了三明治復(fù)合梁的振動(dòng)，并利用高階三明治梁模型得到了基于頻率的等效伯努利-歐拉模型梁的彎曲剛度與剪切模量。梁森等[10]利用有限元數(shù)值模擬建立了密排圓形孔蜂窩層芯結(jié)構(gòu)面內(nèi)等效彈性參數(shù)的模擬模型，該模型獲得的面內(nèi)等效彈性參數(shù)受限于試驗(yàn)或仿真的計(jì)算點(diǎn)。WANG等[11]建立了無(wú)限大蜂窩夾層結(jié)構(gòu)板的振動(dòng)控制方程，并且計(jì)算了無(wú)限大夾層板的隔聲量，但建模時(shí)并未考慮結(jié)構(gòu)板邊界條件的影響。任樹(shù)偉等[12]基于Reissner夾層板理論建立了正六邊蜂窩結(jié)構(gòu)板在四邊簡(jiǎn)支條件下的聲振耦合模型，并結(jié)合流固耦合條件求解了結(jié)構(gòu)的傳聲損失。

綜上所述，為了進(jìn)一步深入研究圓形孔蜂窩夾層結(jié)構(gòu)的隔聲性能，本文利用能量密度法，根據(jù)三明治理論計(jì)算了夾層板層芯的等效剪切模量，基于Reissner理論假設(shè)建立了蜂窩板在四邊簡(jiǎn)支邊界條件下的振動(dòng)耦合方程，根據(jù)流固耦合邊界條件，通過(guò)聲振耦合方程求解了結(jié)構(gòu)的隔聲量。應(yīng)用COMSOL多場(chǎng)耦合軟件對(duì)理論計(jì)算模型進(jìn)行了驗(yàn)證。并討論了蜂窩結(jié)構(gòu)材料和參數(shù)對(duì)其傳聲損失的影響。

1 理論模型建立

1.1 結(jié)構(gòu)參數(shù)等效模型

蜂窩夾層板結(jié)構(gòu)主要由上下面板和蜂窩芯構(gòu)成，如圖1所示。根據(jù)Reissner夾層板理論假設(shè)，假定上下面板僅承受面內(nèi)軸力，蜂窩芯承受橫向剪力。并且考慮到芯層較軟，忽略層芯中平行于x-y平面的應(yīng)力分量，即在芯層中，σx=σy=τxy=0。同時(shí)假定層芯和表層中εz=0，σz=0。圓形孔蜂窩結(jié)構(gòu)上下面板長(zhǎng)為a，寬為b，厚度為d，蜂窩芯壁厚為t，芯層高度為h，圓形胞元直徑為R。圖1為圓形孔蜂窩結(jié)構(gòu)示意圖[13]。

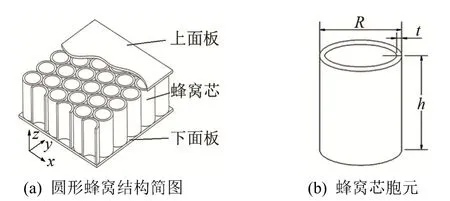
圖1 圓形孔蜂窩結(jié)構(gòu)示意圖[13]Fig.1 Sketch diagram of circular honeycomb structure[13]

根據(jù)Reissner夾層板理論假設(shè)，蜂窩夾層板的彎曲性能主要由上下面板決定，而剪切性能主要由蜂窩芯層決定。因此，對(duì)圓形孔蜂窩結(jié)構(gòu)層芯進(jìn)行三明治夾層板理論等效分析時(shí)，僅計(jì)算其等效剪切模量。三明治等效理論是將層芯和上下面板分開(kāi)考慮，忽略上下面板的橫向剪切變形，僅考慮蜂窩層芯具有剪切變形能力和相當(dāng)?shù)拿鎯?nèi)剛度，將層芯等效為與原尺寸大小相同的均勻等質(zhì)正交異性層，如圖2所示，其中t為蜂窩芯壁厚，R為圓形胞元直徑，h為芯層厚度。當(dāng)蜂窩芯在xy平面內(nèi)作用剪切力Qxz時(shí)，則在蜂窩壁格上產(chǎn)生剪應(yīng)力τc，蜂窩芯代表單元體上受到剪流作用，壁格上所受的剪力為

根據(jù)材料力學(xué)，壁格上單位體積變形能為

其中，G為材料剪切模量，代表單元應(yīng)變能為

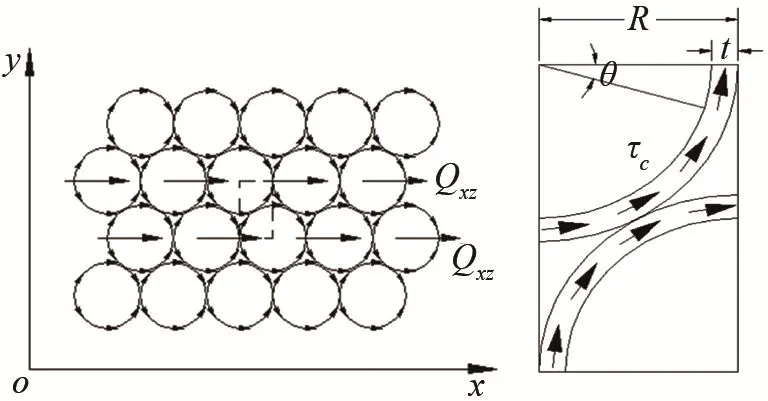
圖2 剪應(yīng)力在蜂窩壁格上的傳遞情況Fig.2 Distribution and transfer of shear stress on the honeycomb lattice

若等效均質(zhì)單元體所受剪應(yīng)力為τxz，則有

等效均質(zhì)體單元體變形能為

其中，Gcxz為xz面內(nèi)的等效剪切模量。如圖2所示，結(jié)構(gòu)在x軸上的剪力Qxz為

根據(jù)應(yīng)變能等效原理，即Uc=U，可解得xz面內(nèi)的等效剪切模量為

同理可得yz面內(nèi)的等效剪切模量，與xz面內(nèi)的等效剪切模量相同，即有

引入廣義位移φx、φy，分別表示夾層板變形前垂直于中面的直線段在變形后的轉(zhuǎn)角，w表示中面撓度。建立以廣義位移φx、φy和w表示的平衡方程[13]：

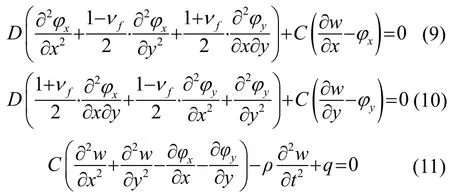
其中：D為結(jié)構(gòu)的抗彎剛度，fν分別為蜂窩上下面板材料彈性模量和泊松比；C為蜂窩層芯剪切剛度。x方向和y方向結(jié)構(gòu)的等效剪切模量相同，即為夾層板單位面積的質(zhì)量，有為面板的密度，ρe為層芯等效密度，對(duì)于圓形孔蜂窩結(jié)構(gòu)為芯層材料密度。引入位移函數(shù)?和f，廣義位移可表示為

將式(12)～(14)代入式(9)～(11)，可得結(jié)構(gòu)板振動(dòng)控制方程

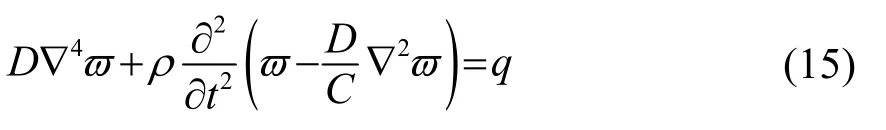
對(duì)于面板x方向長(zhǎng)度為a，y方向長(zhǎng)度為b的蜂窩結(jié)構(gòu)，其四邊簡(jiǎn)支的邊界條件需滿足

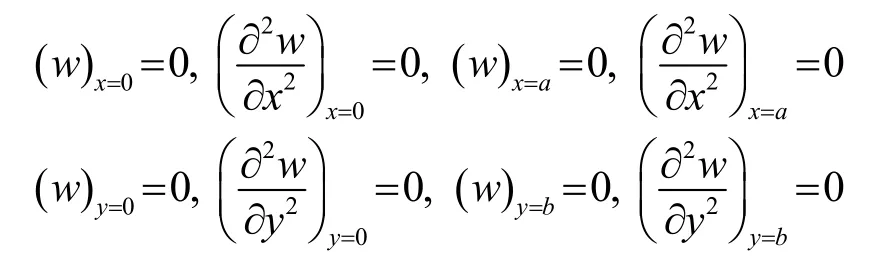
最后可解得蜂窩板結(jié)構(gòu)的振動(dòng)固有頻率為

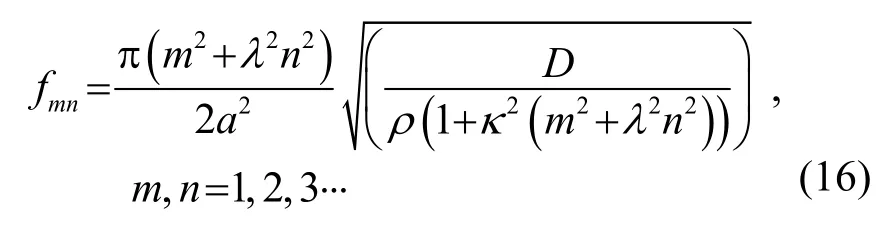
1.2 聲振耦合理論模型

對(duì)于上面板的入射聲壓可表示為

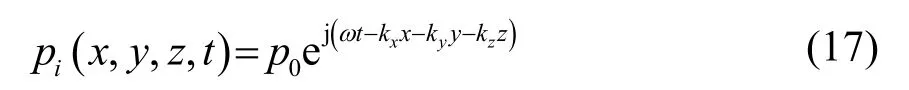
式中，p0為入射波聲壓，ω為聲波圓頻率，kx、ky、kz分別為波數(shù)在坐標(biāo)軸上的分量，并且kx=k0sin?cosθ，ky=k0sin?sinθ，kz=k0cos?，其中k0=ω/c為空氣中聲波波數(shù)，c為聲波在空氣中的傳播速度。?為仰角，即入射波方向與z軸的夾角。θ為方位角，即入射波在xy平面上的投影與x軸的夾角。對(duì)入射波進(jìn)行傅里葉變換，即有

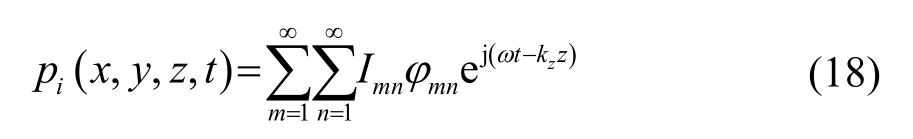
反射聲壓用簡(jiǎn)支模態(tài)級(jí)數(shù)可表示為

透射聲壓用簡(jiǎn)支模態(tài)級(jí)數(shù)可表示為

式(19)、(20)中，βmn為第mn階反射聲壓的幅值，εmn為第mn階透射聲壓的幅值。在聲波激勵(lì)的作用下，蜂窩板振動(dòng)控制方程可表示為

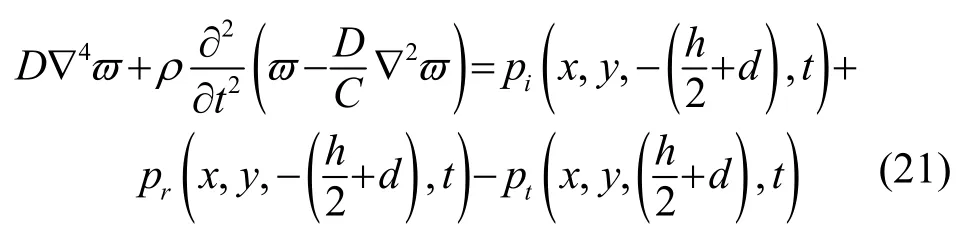
這里取z=0的坐標(biāo)面為夾層板的中面，結(jié)合流固耦合條件有

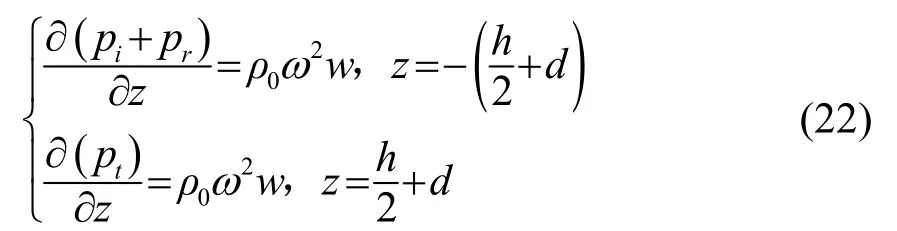
式中，ρ0為空氣密度。定義結(jié)構(gòu)傳聲損失STL為

式中，iW、Wt分別為入射聲功率與透射聲功率，總聲功率W表示為

式中，Re代表取復(fù)數(shù)實(shí)部，A為波陣面截面積，*代表復(fù)數(shù)共軛標(biāo)志。v=p/(ρ0c)為當(dāng)?shù)亓黧w質(zhì)點(diǎn)速度。將聲功率的比值表示為雙級(jí)數(shù)中各項(xiàng)系數(shù)模的平方和之比，可得結(jié)構(gòu)板傳聲損失為[12]

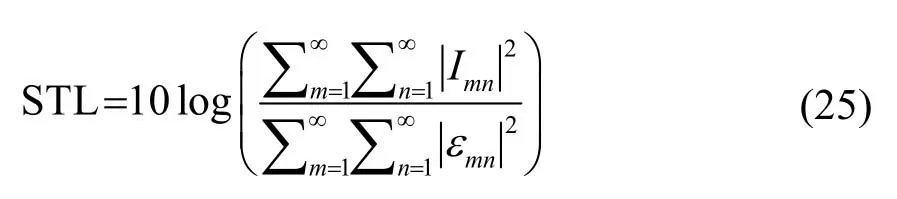
其中，Imn和εmn分別為入射聲壓、透射聲壓第mn階的幅值。

2 數(shù)值仿真分析

COMSOL軟件具有高效的計(jì)算性能和獨(dú)特的全耦合分析能力，其聲學(xué)模塊的數(shù)值仿真分析也具有高度的精確性和可靠性[14]。為驗(yàn)證理論模型的正確性，利用COMSOL軟件對(duì)圓形孔蜂窩結(jié)構(gòu)板進(jìn)行建模，計(jì)算其在簡(jiǎn)支邊界條件下的隔聲量。模型尺寸參數(shù)如表1所示。

在對(duì)蜂窩夾層結(jié)構(gòu)建模時(shí)，首先，有限元模型最大單元尺寸小于最高計(jì)算頻率對(duì)應(yīng)波長(zhǎng)的1/6。其次，驗(yàn)證模型中最高計(jì)算頻率選取為6 kHz。另外對(duì)蜂窩上下面板及芯層單元都設(shè)為殼單元。COMSOL軟件分析時(shí)，物理場(chǎng)選取為三維空間里頻域下的聲-殼相互作用。有限元仿真模型如圖3所示。

表1 模型尺寸參數(shù)Table 1 Dimension parameters of the model

圖3 有限元仿真模型圖Fig.3 Diagram of the finite element simulation model

針對(duì)四邊簡(jiǎn)支的蜂窩夾層結(jié)構(gòu)，利用COMSOL軟件仿真數(shù)值結(jié)果與由式(16)計(jì)算得到的各階固有頻率理論解的對(duì)比情況如表2所示。

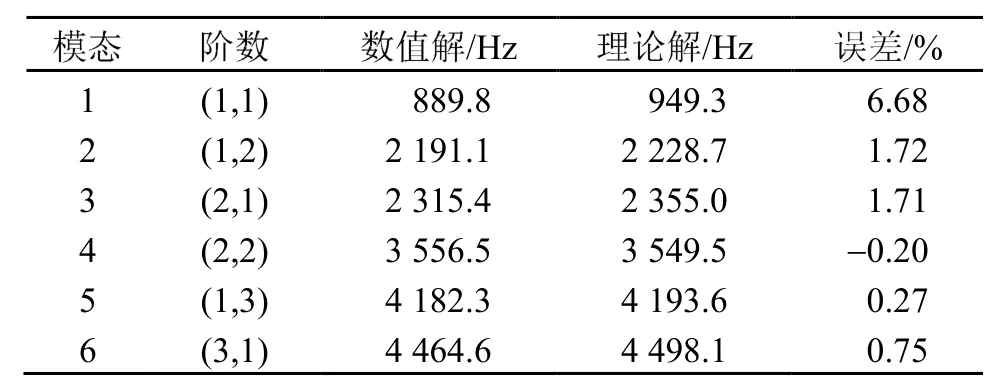
表2 固有頻率的理論解與數(shù)值解對(duì)比Table 2 The theoretical solution versus the numerical solution of inherent frequency

由表2可知，蜂窩夾層結(jié)構(gòu)的固有頻率仿真結(jié)果與理論結(jié)果基本一致，除第一階固有頻率誤差為6.68%外，其余誤差基本在2%以下。由此可認(rèn)為理論模型是準(zhǔn)確的。

為了驗(yàn)證理論模型對(duì)蜂窩夾層結(jié)構(gòu)傳聲損失計(jì)算的影響，以四邊簡(jiǎn)支蜂窩夾層結(jié)構(gòu)為例，對(duì)于式(25)中的傳聲損失計(jì)算，在此取m=n=100時(shí)，能保證結(jié)算結(jié)果的收斂與準(zhǔn)確[12]。利用COMSOL軟件仿真數(shù)值結(jié)果與式(25)計(jì)算得到的蜂窩夾層結(jié)構(gòu)的傳聲損失的對(duì)比情況如圖4所示。

由圖4可知，蜂窩夾層結(jié)構(gòu)的傳聲損失的仿真結(jié)果與計(jì)算結(jié)果基本一致。在一階傳聲損失波谷對(duì)應(yīng)的頻率與蜂窩夾層結(jié)構(gòu)第一階固有頻率一一對(duì)應(yīng)，這是因?yàn)樵诠逃蓄l率附近結(jié)構(gòu)產(chǎn)生共振，聲輻射能量增大，傳聲損失相應(yīng)減小。圖4結(jié)果也說(shuō)明利用本文的等效模型來(lái)求解蜂窩夾層結(jié)構(gòu)的傳聲損失是可行的。

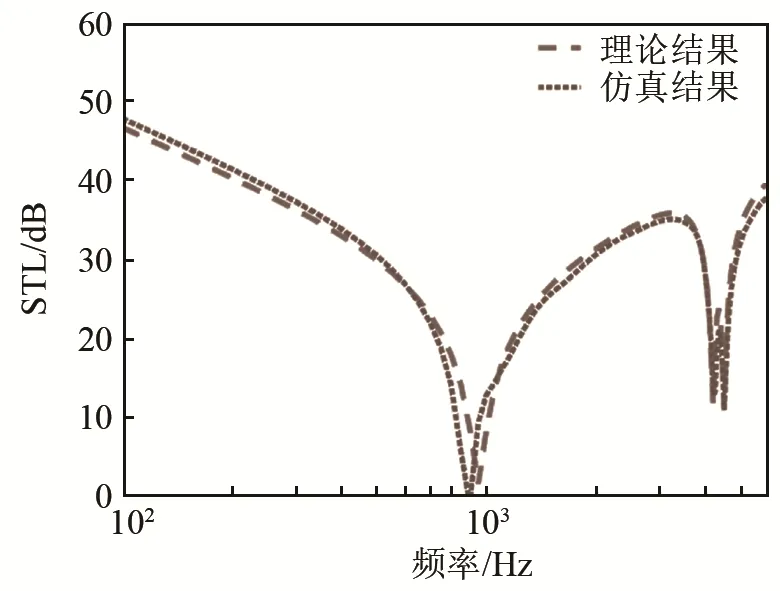
圖4 隔聲量理論計(jì)算與仿真結(jié)果對(duì)比Fig.4 The theoretical calculation versus the numerical simulation of sound transmission loss

3 結(jié)構(gòu)參數(shù)對(duì)隔聲量影響

假設(shè)四邊簡(jiǎn)支條件下的圓形蜂窩夾層結(jié)構(gòu)參數(shù)如表3所示。

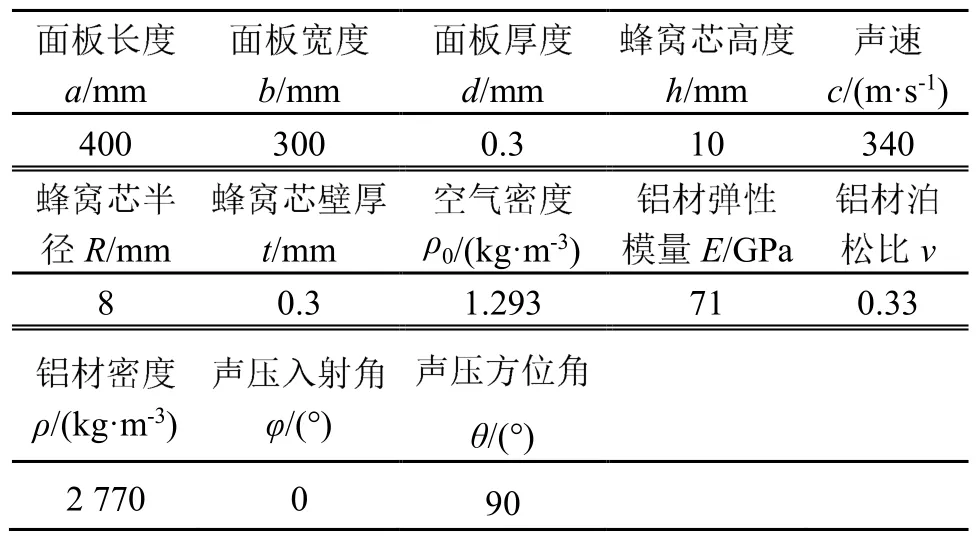
表3 四邊簡(jiǎn)支圓形蜂窩夾層結(jié)構(gòu)參數(shù)Table 3 Structural parameters of circular honeycomb sandwich with simply supported four sides

3.1 芯層胞元半徑

蜂窩芯胞元半徑對(duì)傳聲損失的影響主要來(lái)自于其對(duì)蜂窩夾層板結(jié)構(gòu)的等效面密度和剪切剛度的影響。為了討論蜂窩芯胞元半徑對(duì)蜂窩夾層結(jié)構(gòu)傳聲損失的影響，在其他蜂窩夾層結(jié)構(gòu)參數(shù)保持不變的情況下，蜂窩芯胞元半徑分別取4、8 mm和15 mm，利用式(25)得到三種蜂窩芯胞元半徑對(duì)結(jié)構(gòu)傳聲損失的影響，如圖5所示。

由圖5可知，隨著蜂窩夾層結(jié)構(gòu)的層芯胞元半徑的增大，蜂窩夾層結(jié)構(gòu)的隔聲量下降，但隔聲波谷向高頻偏移。這主要是由于胞元半徑的增大導(dǎo)致蜂窩夾層結(jié)構(gòu)的等效面密度減小，剪切剛度減小，使得蜂窩夾層結(jié)構(gòu)的固有頻率增大。頻率越低，蜂窩夾層結(jié)構(gòu)的層芯胞元半徑對(duì)結(jié)構(gòu)的傳聲損失影響越小。高頻內(nèi)蜂窩夾層結(jié)構(gòu)的層芯胞元半徑對(duì)結(jié)構(gòu)的傳聲損失影響較大。因此，通過(guò)減小層芯胞元半徑可在一定程度提高結(jié)構(gòu)的隔聲性能，但過(guò)小的層芯半徑會(huì)明顯增加結(jié)構(gòu)質(zhì)量，從而增加結(jié)構(gòu)材料成本。

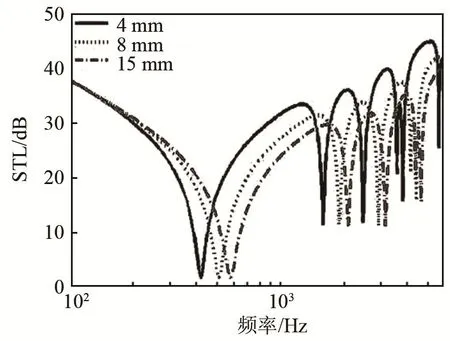
圖5 蜂窩層芯胞元半徑對(duì)結(jié)構(gòu)傳聲損失隨頻率變化的影響Fig.5 The effect of the core radius of circular honeycombon the change of STL with frequency

3.2 蜂窩層芯壁厚

蜂窩層芯壁厚對(duì)蜂窩層芯的剪切剛度和等效密度有一定影響，從而影響蜂窩結(jié)構(gòu)的傳聲損失。保持蜂窩夾層結(jié)構(gòu)的其他參數(shù)不變，分別選取0.05、0.3、1 mm的三種壁厚，分析每種情況下蜂窩夾層結(jié)構(gòu)的傳聲損失變化，具體如圖6所示。

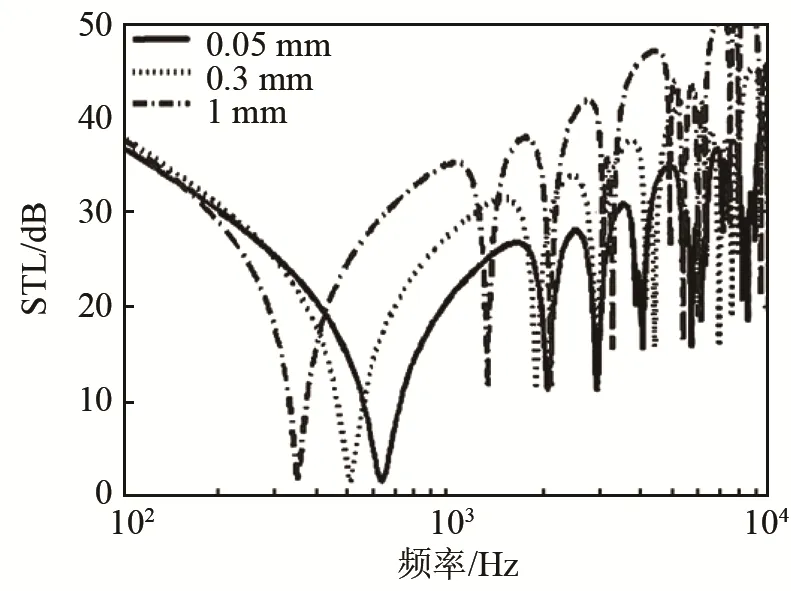
圖6 蜂窩層芯壁厚對(duì)結(jié)構(gòu)傳聲損失隨頻率變化的影響Fig.6 The effect of the wall thickness of circular honeycomb on the change of STL with frequency

由圖6可知，隨著蜂窩層芯壁厚的增大，蜂窩夾層板的傳聲損失增大，對(duì)應(yīng)一階隔聲波谷向低頻移動(dòng)，高階隔聲波谷也向低頻移動(dòng)，這是由于壁厚的增大，結(jié)構(gòu)的剪切剛度增大，結(jié)構(gòu)板固有頻率向低頻偏移，蜂窩層芯的等效密度增大，隔聲量增大。層芯壁厚為1 mm的結(jié)構(gòu)板隔聲量比壁厚0.05 mm的結(jié)構(gòu)板隔聲量平均大15 dB左右。結(jié)構(gòu)板的模態(tài)密度都隨頻率的增大而增大，但在低頻段，結(jié)構(gòu)層芯壁厚對(duì)隔聲量的影響不明顯。上述結(jié)果表明，層芯壁厚的改變明顯影響結(jié)構(gòu)板的隔聲性能[13]。

3.3 結(jié)構(gòu)材料

不同的材料，密度、彈性模量、泊松比不同，導(dǎo)致結(jié)構(gòu)板的隔聲效果也不同。分別研究鋁、鐵、銅三種材料對(duì)夾層板的隔聲性能影響。三種材料的結(jié)構(gòu)參數(shù)和層芯剪切剛度，以及第一階固有頻率如表4所示。蜂窩夾層結(jié)構(gòu)參數(shù)同表3中一致。

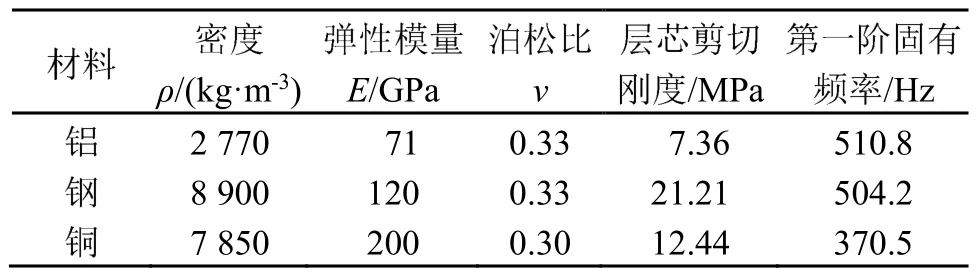
表4 不同材料夾層板物理參數(shù)及對(duì)應(yīng)剪切剛度與一階固有頻率Table 4 Physical parameters and corresponding shear stiffness and first-order natural frequencies of sandwich plates with different materials

利用式(25)可計(jì)算得到蜂窩夾層板結(jié)構(gòu)的傳聲損失隨頻率變化曲線如圖7所示。

圖7 不同結(jié)構(gòu)材料對(duì)結(jié)構(gòu)隔聲量隨頻率變化的影響Fig.7 The effect of the structure material of circular honeycomb on the change of STL with frequency

由圖7可知，蜂窩夾層結(jié)構(gòu)的材料不同，在相同條件下的傳聲損失也不盡相同，其中銅材板的隔聲效果最好。在小于510 Hz低頻范圍內(nèi)，鐵材板的隔聲效果最好。對(duì)尺寸參數(shù)相同的鋁材與鐵材結(jié)構(gòu)，鐵材結(jié)構(gòu)板整體隔聲性能明顯優(yōu)于鋁材結(jié)構(gòu)板。不同材料、相同尺寸的結(jié)構(gòu)板，銅材和鐵材結(jié)構(gòu)板的平均隔聲量比鋁材板高10 dB左右，這主要是由于鋁的密度小、彈性模量小，導(dǎo)致結(jié)構(gòu)板的面密度小、整體剛度低、隔聲效果相對(duì)較差。

4 結(jié) 論

本文通過(guò)計(jì)算等效剪切模量求解了圓形孔蜂窩板結(jié)構(gòu)的傳聲損失，應(yīng)用COMSOL有限元軟件驗(yàn)證了理論模型，并分析了影響圓形孔蜂窩結(jié)構(gòu)傳聲損失的參數(shù)。

(1)利用本文等效參數(shù)計(jì)算圓形蜂窩夾層結(jié)構(gòu)的傳聲損失是可行的。

(2)對(duì)于四邊簡(jiǎn)支的圓形孔蜂窩夾層板結(jié)構(gòu)而言，隨著圓形孔蜂窩層芯胞元半徑的增大，傳聲損失下降，但蜂窩層芯胞元半徑對(duì)低頻段隔聲性能影響并不明顯；同時(shí)隨著蜂窩芯層壁厚增大，蜂窩板的傳聲損失也隨之提高；蜂窩結(jié)構(gòu)材料不同，其傳聲損失也有所差異。